练习题总结1
Clock
读题可以得到:每个时钟有 \(d_i\) 的刻度(第一个有 \(60\) 刻度)
题目给的时间起点和终点,不如看成时间从 \(0\) 开始,且每个时钟都是 \(0\) 刻度,则最后每个时钟的刻度有可以确定,类似进制,只不过每一位的 \(B\) 值可以不一样。
题目中调整时钟可顺可逆,但是会影响比其慢的时钟,不妨设每个时钟转不到两圈,则转 \(i\) 最多影响 \(i+1\) 一个刻度,可以 dp 背包。
注:如果逆时针转,则就是转一圈多一点,然后只用调整 \(D_i - val_i\) 个刻度角度
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const double pi = acos(-1.0);
int n, d[53], l[53];
int val[53]; // 目标刻度
double cost[53]; // 调一刻度所需最小花费
double dp[53][2];// 0调到了vali, 1调到了vali + 1
int main(){
freopen("clock.in", "r", stdin);
freopen("clock.out", "w", stdout);
cin >> n, d[1] = 60;
for(int i = 2; i <= n; i++) cin >> d[i]; // 每个时钟有 di 个刻度
for(int i = 1; i <= n; i++) cin >> l[i];
LL T1, T2, T;
cin >> T1 >> T2, T = max(T1-T2, T2-T1);
for(int i = 1; i <= n; i++) val[i] = T % d[i], T /= d[i]; // 类似进制,只不过每一位的 B 都不同
cost[1] = 2.0 * pi * l[1] / double(d[1]);
for(int i = 2; i <= n; i++){
cost[i] = min(cost[i - 1] * d[i - 1], 2.0 * pi * l[i] / double(d[i]));
}
for(int i = n; i >= 1; i--){
dp[i][0] = min(dp[i + 1][0] + cost[i] * val[i] /* 顺着转 */ , dp[i + 1][1] + cost[i] * (d[i] - val[i]) /* 逆着转 */ );
dp[i][1] = min(dp[i + 1][0] + cost[i] * (val[i] + 1) /* 顺着转 */ , dp[i + 1][1] + cost[i] * (d[i] - val[i] - 1) /* 逆着转 */ );
}
cout << fixed << setprecision(6);
cout << dp[1][0];
return 0;
}
Arrays
有很多性质:
- 对于三个数 \(a,b,c\),满足 \((a - b)c\) 最小,则 \(a,b,c\) 的大小关系固定 \(b < c < a\)
- 不妨设 \(b < c < a\),得到 \(x = (a - b)c\),\(y = (c - b)a\),\(z = (a - c)b\)
- 易得 \(x > y\) 和 \(x > z\)
- 对于选出的 \(n\) 个三元组 \((b_i,c_i,a_i)\) ,有 \(a_i \ge a_{i+1}\) 和 \(c_i \ge c_{i + 1}\) 和 \(b_i \le b_{i + 1}\)
- 将要求的答案拆开来看,得到 \(a_ic_i\) 和 \(-b_ic_i\)
- 设 \(S = \sum\limits_{i=1}^{n}{c_i}\),不放看作 \(S\) 被分为了 \(n\) 份
- 对于 \(a\) 来说,一定大的配大的。对于 \(b\) 来说,一定小的配大的。
- \(b\) 一定是选择序列前 \(n\) 小的
- 反证法,做差法
- 如果不选择前 \(n\) 小,则必定有一个 \(c_i < b_j\)
- 目前答案为 \(ans = (a_i-b_i)c_i + (a_j-b_j)c_j\),若交换 \(b_j\) 和 \(c_i\) 则新答案为 \(nans = (a_i-b_i)b_j + (a_j-c_i)c_j\)
- \(nans - ans = (b_j - c_i)c_j + a_i(b_j - c_i) - (b_j - c_i)b_i\),差值必定大于 0,则 \(nans > ans\)
- 不存在 \(c_i < c_j < a_j < a_i\)。若序列从小到大排序,则选出的 a 和 c 从小到大依次配对
- 证法类似(或直接根据第二个结论)
接下来就可以状压 dp 了?
- 显然配对的 \(a_i\) 和 \(c_i\) 之间的距离最多 \(n + 1\)
看看代码也许有帮助。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
inline int read(){
register int x = 0, t = 1;
register char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') t=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*t;
}
int n, v[103], a[103], b[103], dp[(1ll << 25)];
int i, j, _i, __i;
int C(int x){
int ret = 0;
for(; x > 0; x &= x-1) ret++;
return ret;
}
void work(){
for(i = 1; i <= 3 * n; i++) v[i] = read();
stable_sort(v + 1, v + 1 + 3 * n);
for(i = 1; i <= n; i++) b[i] = v[i];
for(i = 1; i <= 2 * n; i++) a[2 * n - i + 1] = v[n + i];
for(i = 0; i < (1ll << n); i++) dp[i] = 0;
for(i = 0; i < (1ll << n) - 1; i++){
int cnt = C(i), p = 1; // 意外发现当前配对了多少对,即状态中 1 的个数
while((i >> (p-1)) & 1) p++;
_i = (i | (1ll << (p-1))) >> 1;
for(j = n; j > p - 1; j--){
if((_i >> (j-1)) & 1) break;
__i = _i | (1ll << (j-1)); // 意发现 __i 必定大于 i,自然滚动
dp[__i] = max(dp[__i], dp[i] + (a[cnt + p] - b[cnt + 1]) * a[cnt + j + 1]);
}
}
cout << dp[(1ll << n) - 1] << "\n";
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
//freopen("arrays.in", "r", stdin);
//freopen("arrays.out", "w", stdout);
int T = read();
n = read();
while(T--) work();
return 0;
}
Funny Strings
首先必须知道:A 可以通过旋转得到 B,当且仅当存在一个 \(L\),使得 \(A_{i} = B_{(i + L) \bmod n}\)
关于构造,首先可以想到所有的值设为 \(\left\lfloor\frac{k}{n}\right\rfloor\),那么还有 \(k \bmod n\) 个 1 需要加(显然这是最好的一种构造方法之一)。
由于还有一个限制,所以有一个 1 需要加在 \(a_n\) 上。
接下来只用找到一个 \(L\) 满足,从 \(n\) 开始,走 \(k\bmod n\) 步(每次从 \(x\) 走到 \((x + L - 1) % n + 1\))可以恰好走会 \(n\),可以直接枚举 \(L\),然后 \(O(1)\) 计算判断合法性。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int n, k, a[1003];
int main(){
cin >> n >> k;
int S = k / n, len = 0;
k %= n;
for(len = 0; (k * len + 1) % n > 0; len++){
}
int x = len;
while(k--){
a[x] = 1;
x = (x + len) % n;
}
for(int i = 0; i < n; i++){
cout << S + a[i] << " ";
}
return 0;
}
Password
对于区间异或操作,显然可以设 \(b_i = a_i \oplus a_{i-1}\),则可以将目标序列转化为 \(b\) 序列,则最多有 \(2k\) 个 1。
对于区间操作,则每次就是选择 \(i\) 和 \(i + a_j\) 同时异或 1。
则问题成了一个 \(2k\) 个点配对的问题。
注意:不能只从 0 长度开始 BFS,因为有 \(1\) 到 \(n\) 的限制。所以需要 \(2k\) 个点中的每个点开始一次 BFS。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e4 + 3;
int n, k, L;
int a[MAXN], len[203];
int cost[MAXN], _cost[23][23];
int dp[(1ll << 20)];
vector<int> vt;
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> k >> L, n++;
for(int i = 1, x; i <= k; i++){
cin >> x, a[x] ^= 1, a[x + 1] ^= 1;
}
for(int i = 1; i <= L; i++){
cin >> len[i];
len[L + i] = -len[i];
}
L *= 2;
for(int i = 1; i <= n; i++){
if(a[i]) vt.push_back(i);
}
k = vt.size();
for(int I = 0; I < vt.size(); I++){ int S = vt[I];
queue<int> que;
for(int i = 1; i <= n; i++) cost[i] = 1e9;
que.push(S), cost[S] = 0;
while(!que.empty()){
int i = que.front();
que.pop();
for(int j = 1; j <= L; j++){
int _i = i + len[j];
if(_i >= 1 && _i <= n && cost[_i] >= 1e9){
cost[_i] = cost[i] + 1, que.push(_i);
}
}
}
for(int J = 0; J < vt.size(); J++){
_cost[I][J] = cost[vt[J]];
}
}
for(int i = 0; i < (1ll << k); i++) dp[i] = 1e9;
dp[0] = 0;
for(int i = 0; i < (1ll << k); i++){
for(int x = 1; x <= k; x++){
if((i >> (x-1)) % 2 == 1) continue;
for(int y = x + 1; y <= k; y++){
if((i >> (y-1)) % 2 == 1) continue;
int _i = i | (1ll << (x-1)) | (1ll << (y-1));
dp[_i] = min(dp[_i], dp[i] + _cost[x-1][y-1]);
}
}
}
int ans = dp[(1ll << k) - 1];
cout << (ans >= 1e9 ? -1 : ans);
return 0;
}
线性规划
练习题
拉格朗日定理
Perils in Parallel
灵魂拷问:你真的学会dfs了吗?
题目显然差分后,转化成,每个点有0或1的点券,选择一条边可以将两端点的点权都异或1,要求最后所有点权都为0。
然后就dfs。显然是dfs出dfs树,然后从树的叶子向上遍历。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 2e5 + 3;
struct Node{
int a, b;
}v[MAXN];
int n, m, opt[MAXN], d[MAXN], vis[MAXN], _vis[MAXN];
vector<PII> eg[MAXN];
vector<int> ans;
void init(){
cin >> n >> m;
for(int i = 1; i <= n; i++){
cin >> v[i].a >> v[i].b;
}
sort(v + 1, v + 1 + n, [](Node i, Node j){ return i.a < j.a; });
for(int i = 1; i <= n; i++) opt[i] = v[i].b;
for(int i = 1, vl, vr, L, R; i <= m; i++){
cin >> vl >> vr;
int l = 1, r = n;
while(l < r){
int mid = (l + r) >> 1;
if(v[mid].a >= vl){
r = mid;
}else l = mid + 1;
}
if(v[l].a < vl) continue;
L = l, l = 1, r = n;
while(l < r){
int mid = (l + r + 1) >> 1;
if(v[mid].a <= vr){
l = mid;
}else r = mid - 1;
}
if(v[l].a > vr) continue;
R = l;
eg[L].push_back({R + 1, i}), eg[R + 1].push_back({L, i});
d[L]++, d[R + 1]++;
}
}
void dfs(int x){
_vis[x] = 1;
for(PII e : eg[x]){ int nxt = e.first;
if(!_vis[nxt]){
dfs(nxt);
if(opt[nxt]){
opt[nxt] ^= 1, opt[x] ^= 1, ans.push_back(e.second);
}
}
}
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
init();
n++;
for(int i = n; i >= 1; i--) opt[i] ^= opt[i - 1];
for(int i = 1; i <= n; i++){
if(!_vis[i]) dfs(i);
}
for(int i = 1; i <= n; i++){
if(opt[i]){
cout << -1;
return 0;
}
}
cout << ans.size() << "\n";
sort(ans.begin(), ans.end());
for(int x : ans) cout << x << " ";
return 0;
}
Interesting Trip
再来一题,你真的学会 dfs 了吗?
题目给的一个 DAG,字典序比较需要从终点状态向起点状态比较,否则会受到长度影响。
那么思路就有了,可是如何快速实现?利用倍增套哈希,用于比较。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 2e5 + 3;
const int MAXL = 20;
const LL mod = 1e9 + 7, B = 233;
int n, m, S, T, to[MAXN];
string s;
vector<int> eg[MAXN];
bool vis[MAXN];
LL Hash[MAXL][MAXN], anc[MAXL][MAXN];
bool cmp(int x, int y){
for(int l = MAXL - 1; l >= 0; l--){
if(Hash[l][x] == Hash[l][y]) x = anc[l][x], y = anc[l][y];
}
return s[x] < s[y];
}
void dfs(int x){
if(x == T){
to[x] = n + 1;
return;
}
vis[x] = 1;
int y = 0;
for(int nxt : eg[x]){
if(!vis[nxt]){
dfs(nxt);
}
if(!to[nxt]) continue;
if(!y || s[nxt] < s[y] || cmp(nxt, y)){
y = nxt;
}
}
to[x] = y;
if(y > 0){
LL _B = B;
anc[0][x] = y, Hash[0][x] = s[x] - 'a' + 1;
for(int l = 1; l < MAXL; l++){
anc[l][x] = anc[l-1][anc[l-1][x]];
Hash[l][x] = (Hash[l-1][x] * _B % mod + Hash[l-1][anc[l-1][x]]) % mod;
_B = _B * _B % mod;
}
}
}
int main(){
cin >> n >> m >> s;
s = "a" + s + "zzz";
for(int i = 1, U, V; i <= m; i++){
cin >> U >> V;
eg[U].push_back(V);
}
cin >> S >> T;
dfs(S);
if(!to[T]){
cout << "No way";
}else{
for(int x = S; x <= n && x > 0; x = to[x]){
cout << s[x];
}
}
return 0;
}
String Cards
不妨将字符串看作数字,则这道题:https://www.luogu.com.cn/problem/P1012
你可能遇到过这样的数据:
2 2
b
ba
想要多个数字拼起来最小,则按 \(s_i + s_j < s_j + s_i\) 排序,证明如下:
- 设 \(s_i\) 的数位为 \(n\),\(s_j\) 的数位为 \(m\),\(a_i\) 为 \(s_i\) 的数字形式。
- \(s_i + s_j < s_j + s_i\) 等价于 \(a_i * 10^m + a_j < a_j * 10^n + a_i\)
- 推式子:
- \(a_i * (10^m - 1) < a_j * (10^n - 1)\)
- \(\dfrac{a_i}{10^n - 1} < \dfrac{a_j}{10^m - 1}\)
- 这不恰好 \(n\) 对应 \(a_i\),\(m\) 对应 \(a_j\)
- 可以证明两个分数分别是以 \(a_i\) 为循环节的小数 和 以 \(a_j\) 为循环节的小数(该证明在后面)
- 所以 \(s_i + s_j < s_j + s_i\) 等价于 \(s_i + s_i + \cdots < s_j + s_j + \cdots\)
- 终于我们分清了这种排序的本质,那么接下来就可以口糊贪心了
- 所有数字拼在一起,必定要求第一位相等,直到长度最小的 \(s_i\),
如何证明那两个分数。
- 对于一个以 \(s\) 为循环节的小数,我们设其为 \(x\) 满足 \(0 < x < 1\)
- 显然 \(x * 10^{|s|} - s = x\),得到 \(x = \dfrac{s}{10^{|s|} - 1}\)。
- 所以 \(\dfrac{s}{10^{|s|} - 1}\) 以 \(s\) 为循环节
那该如何dp?立马想到的做法就是从前往后背包,但是又会被开头的那个数据卡,为什么?
因为你长度不确定,可能匹配偏了,所以要么从前往后但是背包目前总长度,要么从后往前
P4813 [CCO2014] Troy 与三角形
小清新递推题。
考虑枚举三角形的最上方的点(顶点),设 \(a_{i,j}\) 表示以 \((i,j)\) 为顶点向下最大的 \(h\) 为多少。
发现二分没用,倍增也没用,考虑前缀和?不妨看做给的是一个完整三角形,则显然有 \(a_{i,j} = a_{i + 1, j} + 1\),如何推广?
显然有 \(a_{i,j} = \min(a_{i+1,j}, a_{i+1,j-1}, a_{i+1,j+1}) + 1\)。为什么这样,因为灵光一现
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 2000 + 3;
int n;
char ch[MAXN][MAXN];
int dp[MAXN][MAXN];
int main(){
cin >> n;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
cin >> ch[i][j];
}
}
LL ans = 0;
for(int j = 1; j <= n; j++){
if(ch[n][j] == '#') ans++, dp[n][j] = 1;
}
for(int i = n - 1; i >= 1; i--){
for(int j = 1; j <= n; j++){
if(ch[i][j] == '#'){
dp[i][j] = min({dp[i + 1][j], dp[i + 1][j + 1], dp[i + 1][j - 1]}) + 1;
ans += dp[i][j];
}
}
}
cout << ans;
return 0;
}
P3760 [TJOI2017] 异或和
做法1:
考虑答案的每一位。设当前枚举到第 \(k\) 位,再枚举右端点 \(r\),则现在问题转化为:快速求出 \(\bigoplus_{i=1}^{r}{s_r - s_{i-1}}\) 中第 \(k\) 位的值。
由于只用考虑一位,那么减法和二进制有什么关系?进位!!!
首先注意:我们有 \(s_l \le s_r\)
如果当前扫描到的 \(s_i\) 的二进制第 \(k\) 位为 \(1\),那么对这一位的答案有贡献的只有那些第 \(k\) 位为 \(1\) 且第 \(k\) 位向右的数比 \(s_i\) 第 \(k\) 位向右的数大的,或者第 \(k\) 位为 \(0\) 且第 \(k\) 位向右的数不比 \(s_i\) 第 \(k\) 位向右的数大的。
因为如果第 \(k\) 位都为 \(1\) 的话,那么只有后面那些位的和大于 \(s_i\) 的数,\(s_i\) 减去它之后第 \(k\) 位才能出现 \(1\)。
接下来就可以用权值树状数组维护了。复杂度 \(O(n \log^2)\),但是常数和空间都很小。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e5 + 3, V = 1e6;
int n, s[MAXN];
int sum[2][V+3];
int QUE(int op, int x){
x++;
int ret = 0;
for(; x > 0; x -= (x & (-x))) ret += sum[op][x];
return ret;
}
void ADD(int op, int x, int w){
x++;
for(; x <= V+1; x += (x & (-x))) sum[op][x] += w;
}
int main(){
cin >> n;
for(int i = 1; i <= n; i++){
cin >> s[i], s[i] += s[i - 1];
}
int ans = 0;
for(int b = 0; b < 20; b++){
int w = (1ll << b) - 1, cnt = 0;
for(int i = 0; i <= V + 1; i++) sum[0][i] = sum[1][i] = 0;
ADD(0, 0, 1);
for(int i = 1; i <= n; i++){
int op = ((s[i] & (1ll << b)) > 0 ? 1 : 0);
if(op > 0){
cnt ^= (QUE(0, s[i] & w) + QUE(1, V) - QUE(1, s[i] & w)) & 1;
}else{
cnt ^= (QUE(1, s[i] & w) + QUE(0, V) - QUE(0, s[i] & w)) & 1;
}
ADD(op, s[i] & w, 1);
}
if(cnt) ans += (1ll << b);
}
cout << ans;
return 0;
}
做法2:
使用01-trie
考虑从 \(n\) 到 \(1\) 枚举 \(l\),则贡献会转化:\((s_n-s_l) \oplus (s_{n-1} - s_l) \cdots (s_{l+1} - s_l) \to (s_n-s_l+a_l) \oplus (s_{n-1} - s_l+a_l) \cdots (s_{l+1} - s_l+a_l) \oplus a_l\)
发现 \(\sum\limits_{i=1}^{n}{a_i} \le 10^6\),所以可以不断 01-trie 全局加一。具体见:https://www.cnblogs.com/huangqixuan/articles/17664519.html#01-trie-全局加一
复杂度 \(O((\sum\limits_{i=1}^{n}{a_i} + n) \log V)\)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e5 + 3;
int n, a[MAXN];
int eg[MAXN * 23][2], tot = 1, sz[MAXN * 23];
int sum = 0;
void Insert(int x){
int p = 1; sum ^= x;
for(int bit = 0; bit <= 20; bit++){
int col = (x >> bit) & 1;
if(!eg[p][col]) eg[p][col] = ++tot;
p = eg[p][col], sz[p]++;
}
}
void ADD(int x, int bit){ // 全局加一
if(bit > 20) return;
if(eg[x][1]){
ADD(eg[x][1], bit + 1);
}
swap(eg[x][0], eg[x][1]);
if(sz[eg[x][0]] & 1) sum ^= (1ll << bit);
if(sz[eg[x][1]] & 1) sum ^= (1ll << bit);
}
int main(){
cin >> n;
for(int i = 1; i <= n; i++){
cin >> a[i];
}
int ans = 0;
for(int i = n; i >= 1; i--){
int x = a[i];
while(x--) ADD(1, 0);
Insert(a[i]);
ans ^= sum;
}
cout << ans;
return 0;
}
P5014 水の三角(修改版)
卡特兰数的练手好题。
试着把线拉直并且暂时不考虑斜线:
1
|
2 - 3
| |
4 - 5 - 6
则方案数为卡特兰数 \(\dbinom{n + m}{m} - \dbinom{n + m}{m - 1}\)(注意这里的 \(n,m\) 不是点的编号,而是边的个数)。
如果考虑斜线,枚举走 \(i\) 条,则 \(n\) 和 \(m\) 需要同时减去 \(i\),然后求卡特兰数、分别在那些位置走斜边的组合数 的乘积。
答案为 \(\sum\limits_{i=0}^{m}{\dbinom{n+m-i}{i}} (\dbinom{n-i+m-i}{m-i} - \dbinom{n-i+m-i}{m-i-1})\)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const LL mod = 998244353;
const int MAXN = 3e6 + 3;
LL qpow(LL A, LL B){
LL ret = 1;
while(B > 0){
if(B & 1) ret = ret * A % mod;
A = A * A % mod, B >>= 1;
}
return ret;
}
LL fac[MAXN], ifac[MAXN];
LL C(int B, int A){
if(A < 0) return 0;
return fac[B] * ifac[A] % mod * ifac[B - A] % mod;
}
int main(){
fac[0] = 1;
for(int i = 1; i <= 3e6; i++) fac[i] = fac[i - 1] * i % mod;
ifac[int(3e6)] = qpow(fac[int(3e6)], mod - 2);
for(int i = 3e6 - 1; i >= 0; i--) ifac[i] = ifac[i + 1] * (i + 1) % mod;
int T;
cin >> T;
while(T--){
LL u, n = 1, m = 1;
cin >> u;
while(n * (n + 1) / 2 < u) n++;
m = u - n * (n + 1) / 2 + n;
// 转换为行和列,这有 n > m
n--, m--;
LL ans = 0;
for(int i = 0; i <= m; i++){
LL _n = n - i, _m = m - i;
ans = (ans + (C(_n + _m, _m) - C(_n + _m, _m - 1) + mod) % mod * C(_n + _m + i, i) % mod) % mod;
}
cout << ans << "\n";
}
return 0;
}
SP16636 - IE2 - Journey
\(k=0\) 则可以倍增优化dp
对于 \(k>0\) 的部分容斥:
- 设答案为路径总和,但是发现需要减去所有不能经过一个点的路径总和,但是发现需要加上所有不能经过两个点的路径总和......
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const LL mod = 1e9 + 9;
const int MAXL = 32;
int n, m, k, d;
int p[8], V[203], U[203];
bool vis[23];
LL anc[MAXL][23][23], dp[23][23], tmp[23][23];
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m >> k >> d, d--;
for(int i = 1; i <= k; i++){
p[i] = i;
}
for(int i = 1; i <= m; i++){
cin >> U[i] >> V[i];
}
LL ans = 0;
for(int i = 0; i < (1ll << k); i++){
int cnt = 0;
for(int j = 0; j < k; j++){
if((i >> j) % 2 == 0){
vis[p[j + 1]] = 0;
}else cnt++, vis[p[j + 1]] = 1;
}
for(int x = 1; x <= n; x++){
for(int y = 1; y <= n; y++){
for(int l = 0; l < MAXL; l++) anc[l][x][y] = 0;
}
}
for(int e = 1; e <= m; e++){
if(!vis[U[e]] && !vis[V[e]]) anc[0][U[e]][V[e]]++, anc[0][V[e]][U[e]]++;
}
for(int l = 1; l < MAXL; l++){
for(int x = 1; x <= n; x++){
for(int y = 1; y <= n; y++){
for(int z = 1; z <= n; z++){
anc[l][x][z] = (anc[l][x][z] + anc[l-1][x][y] * anc[l-1][y][z] % mod) % mod;
}
}
}
}
for(int x = 1; x <= n; x++){
for(int y = 1; y <= n; y++) dp[x][y] = 0;
}
for(int x = 1; x <= n; x++) if(!vis[x]) dp[x][x] = 1;
for(int l = 0; l < MAXL; l++){
if((d >> l) % 2 == 0) continue;
for(int x = 1; x <= n; x++){
for(int y = 1; y <= n; y++) tmp[x][y] = dp[x][y], dp[x][y] = 0;
}
for(int x = 1; x <= n; x++){
for(int y = 1; y <= n; y++){
for(int z = 1; z <= n; z++){
dp[x][z] = (dp[x][z] + tmp[x][y] * anc[l][y][z] % mod) % mod;
}
}
}
}
LL ret = 0;
for(int x = 1; x <= n; x++){
for(int y = 1; y <= n; y++) ret = (ret + dp[x][y]) % mod;
}
if(cnt % 2 == 0){
ans = (ans + ret) % mod;
}else ans = (ans + mod - ret) % mod;
}
cout << ans % mod;
return 0;
}
New Year Garland
这种算组合数的题目,最好不要看题解,因为可能会误导,只需要知道其利用方法。
先要算出每一行的方案,然后再从从上向下 dp,过程需要减去不合法的方案(容斥)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e6 + 3;
LL mod, fac[MAXN], _fac[MAXN];
int n, m, l[MAXN];
LL g[5003][5003], s[MAXN];
LL f[MAXN], tmp[MAXN];
int main(){
cin >> n >> m >> mod;
for(int i = 1; i <= n; i++){
cin >> l[i];
}
g[0][0] = 1;
for(int i = 1; i <= 5000; i++){
for(int j = 1; j <= i; j++){
g[i][j] = (g[i - 1][j - 1] + g[i - 1][j] * (j - 1) % mod) % mod;
}
}
fac[0] = 1;
for(int i = 1; i <= 1e6; i++) fac[i] = fac[i - 1] * i % mod;
_fac[m + 1] = 1;
for(int i = m; i >= 1; i--) _fac[i] = _fac[i + 1] * i % mod;
s[0] = 1;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= min(l[i], m); j++){
f[j] = _fac[m - j + 1] * g[l[i]][j] % mod * s[i - 1] % mod;
if(j <= l[i - 1]) f[j] = (f[j] - fac[j] * g[l[i]][j] % mod * tmp[j] % mod + mod) % mod;
s[i] = (s[i] + f[j]) % mod;
}
for(int j = 1; j <= min(l[i - 1], m); j++) tmp[j] = 0;
for(int j = 1; j <= min(l[i], m); j++) tmp[j] = f[j];
}
cout << s[n];
return 0;
}
P2964 [USACO09NOV] A Coin Game S
博弈论 dp 好题
Souvenirs
显然问题可以简化为求 \(j < i\) 且 \(a_j \ge a_i\) 的最小 \(a_j - a_i\)(但是需要做两遍)
暴力是枚举出 \(i\) 后,\(j\) 从 \(i\) 向 \(1\) 枚举。如何加速这个过程?或是说如何减少冗余操作?
不断设新加入 \(k\)(从 \(i\) 到 \(1\) 加入那些 \(a_k \ge a_i\) 的),若 \(a_k \ge \dfrac{a_i + a_j}{2}\) 则 \((i,k)\) 必定被 \((j,k)\) 替代(因为 \([j,k] \in [i,k]\) 且答案更小),那么只用找到 \(a_k < \dfrac{a_i + a_j}{2}\) 的 \(k\),每次值域减半,所以最多 \(n \log V\) 个点对需要检查,变为了二维数点问题。
具体解决:权值线段树动态开点,扫描线,树状数组
复杂度:离线 \(O(n \log V \log V + m \log n)\)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
inline LL read(){
LL x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') f = (ch == '-' ? -1 : f), ch = getchar();
while(ch >= '0' && ch <= '9') x = (x<<1) + (x<<3) + (ch^48), ch = getchar();
return x * f; }
void write(LL x){ if(x>9) write(x/10); putchar(x%10+'0'); }
const int MAXN = 3e5 + 3;
const int Inf = 1e9 + 1;
int tmp;
int n, m, ans[MAXN], a[MAXN];
vector<PII> ask[MAXN];
int tr[MAXN*31], ls[MAXN*31], rs[MAXN*31], root = 0, tot = 0;
int sum[MAXN];
inline void _ADD(int x, int w){
for(; x <= n; x += (x & (-x))) sum[x] = min(sum[x], w);
}
inline int _QUE(int x){
int ret = 1e9;
for(; x > 0; x -= (x & (-x))) ret = min(ret, sum[x]);
return ret;
}
inline void ADD(int l, int r, int pos, int &cur){
if(!cur) cur = ++tot;
if(l == r){
tr[cur] = tmp;
return;
}
int mid = (l + r) >> 1;
if(pos <= mid) ADD(l, mid, pos, ls[cur]);
else ADD(mid + 1, r, pos, rs[cur]);
tr[cur] = max(tr[ls[cur]], tr[rs[cur]]);
}
int L, R;
inline int QUE(int l, int r, int cur){
if(!cur) return 0;
if(L <= l && r <= R){
return tr[cur];
}
int mid = (l + r) >> 1, ret = 0;
if(L <= mid && ls[cur]) ret = max(ret, QUE(l, mid, ls[cur]));
if(mid + 1 <= R && rs[cur]) ret = max(ret, QUE(mid + 1, r, rs[cur]));
return ret;
}
void solve(){
for(int i = 1; i <= n; i++) sum[i] = 1e9;
for(int r = 1; r <= n; r++){
L = a[r], R = Inf; int i = QUE(1, Inf, root);
while(i > 0){
//cout << i << " " << r << " " << a[i] << " " << a[r] << "\n";
_ADD(n - i + 1, a[i] - a[r]);
L = a[r], R = (a[i] + a[r] + 1) / 2 - 1, i = QUE(1, Inf, root);
}
tmp = r, ADD(1, Inf, a[r], root);
for(PII q : ask[r]){
ans[q.second] = min(ans[q.second], _QUE(n - q.first + 1));
}
}
for(int i = 0; i <= tot; i++) tr[i] = 0, ls[i] = 0, rs[i] = 0;
root = 0, tot = 0;
}
int main(){
n = read();
for(int i = 1; i <= n; i++){
a[i] = read(), a[i]++;
}
m = read();
for(int i = 1, l, r; i <= m; i++){
l = read(), r = read();
ask[r].push_back({l, i}), ans[i] = 1e9;
}
solve();
for(int i = 1; i <= n; i++) a[i] = Inf - a[i] + 1;
solve();
for(int i = 1; i <= m; i++) write(ans[i]), putchar('\n');
return 0;
}
P5643 [PKUWC2018] 随机游走
参考题解:https://www.luogu.com.cn/article/hbo189ev
考虑 min-max 容斥,则问题可以转化为求起点 \(x\) 到 \(T\) 中某个点的期望步数。
利用 \(dp\),设 \(f_i\) 表示从 \(i\) 出发到达 \(T\) 中的点的期望步数,则有递推式 \(f_i = \dfrac{f_{fa_i} + \sum\limits_{j\in son_i}{f_j}}{deg_i}\)(\(deg_i\) 表示节点 \(i\) 的度数)
考虑待定系数法,设 \(f_i = k_i \times f_{fa_i} + b_i\)......可以推出 \(f_i = \dfrac{1}{deg_i - \sum_{j\in son_i}{k_j}}f_{fa_i} + \dfrac{deg_i + \sum_{j\in son_i}{b_j}}{deg_i - \sum_{j\in son_i}{k_j}}\),对应的 \(k_i\) 和 \(b_i\) 也就知道了。显然属于集合 \(T\) 的点的 \(k_i\) 和 \(b_i\) 都为 \(0\)。
最后从 \(x\) 出发的期望步数为 \(b_x\),所以不用具体求出 \(f\) 的值。最后再上一个高维前缀和就好了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const LL mod = 998244353;
LL qpow(LL A, LL B){
LL ret = 1;
while(B > 0){
if(B & 1) ret = ret * A % mod;
A = A * A % mod, B >>= 1;
}
return ret;
}
int n, Q, root;
vector<int> eg[30];
LL k[30], b[30], s[(1ll << 18)];
bool vis[30];
void dfs(int x, int dad){
if(vis[x]){
k[x] = b[x] = 0;
return;
}
LL deg = eg[x].size();
k[x] = 0, b[x] = 0;
for(int nxt : eg[x]){
if(nxt == dad) continue;
dfs(nxt, x);
k[x] = (k[x] + k[nxt]) % mod, b[x] = (b[x] + b[nxt]) % mod;
}
k[x] = qpow((deg - k[x] + mod) % mod, mod - 2);
b[x] = (deg + b[x]) % mod * k[x] % mod;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> Q >> root;
for(int i = 1, U, V; i < n; i++){
cin >> U >> V;
eg[U].push_back(V), eg[V].push_back(U);
}
for(int t = 1; t < (1ll << n); t++){
int popc = 0;
for(int j = 1; j <= n; j++) vis[j] = 0;
for(int j = 0; j < n; j++) if((t >> j) & 1) vis[j + 1] = 1, popc++;
dfs(root, 0);
s[t] = b[root];
if(popc % 2 == 0) s[t] = (mod - s[t]) % mod;
}
for(int j = 0; j < n; j++){
for(int t = 1; t < (1ll << n); t++){
if((t >> j) % 2 == 0) s[t | (1ll << j)] = (s[t | (1ll << j)] + s[t]) % mod;
}
}
for(int q = 1, k, x; q <= Q; q++){
cin >> k;
int t = 0;
while(k--) cin >> x, t |= (1ll << (x-1));
cout << s[t] << "\n";
}
return 0;
}
CF1641D - Two Arrays
法一:
先有一个容斥方法;https://www.cnblogs.com/huangqixuan/articles/18348990#first
可以 Hash 比较子集,再双指针,然后就是一个 \(O(nm2^m)\) 的做法。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using ULL = unsigned long long;
const int MAXN = 1e5 + 3;
int n, m, popc[(1ll<<5)];
LL b[MAXN][6];
array<int, 6> a[MAXN];
int mp[3200003];
ULL Hash[MAXN][(1ll<<5)];
void ADD(int x, int op){
if(!x) return;
for(int s = 1; s < (1ll << m); s++){
mp[Hash[x][s]] += op;
}
}
int QUE(int x){
if(!x) return 0;
int ret = 0;
for(int s = 1; s < (1ll << m); s++){
if(popc[s] % 2 == 0){
ret -= mp[Hash[x][s]];
}else ret += mp[Hash[x][s]];
}
return ret;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
mt19937_64 rnd(time(0));
map<int, int> cmp;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++) cin >> a[i][j];
cin >> a[i][0];
}
sort(a + 1, a + 1 + n);
for(int i = 0; i < (1ll << m); i++){
for(int j = 0; j < m; j++) popc[i] += (i >> j) & 1;
}
for(int i = 1, cnt = 0; i <= n; i++){
for(int j = 1; j <= m; j++){
if(cmp.find(a[i][j]) == cmp.end()) cmp[a[i][j]] = rnd();
b[i][j] = cmp[a[i][j]];
}
}
vector<pair<ULL, pair<int, int>>> p;
for(int i = 1, cnt = 0; i <= n; i++){
for(int s = 0; s < (1ll << m); s++){
for(int j = 1; j <= m; j++) if((s >> (j-1)) & 1) Hash[i][s] = Hash[i][s] ^ b[i][j];
p.push_back({Hash[i][s], {i, s}});
}
}
sort(p.begin(), p.end());
for(int i = 0, cnt = 0; i < p.size(); i++){
if(i == 0 || p[i].first != p[i - 1].first){
cnt++;
}
Hash[p[i].second.first][p[i].second.second] = cnt;
}
int l = 0, r = 2;
ADD(1, 1);
while(r < n && QUE(r) == r - 1) ADD(r, 1), r++;
if(QUE(r) == r - 1){
cout << -1;
return 0;
}
l = r - 1;
while(l > 0 && QUE(r) != l) ADD(l, -1), l--;
int ans = a[r][0] + a[l + 1][0];
/*
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
cout << a[i][j] << " ";
}
cout << a[i][0] << "\n";
}
cout << "&\n";
*/
for(int i = r + 1; i <= n; i++){
if(l <= 0) break;
if(QUE(i) != l){
while(QUE(i) != l) ADD(l, -1), l--;
if(l < i - 1) ans = min(ans, a[i][0] + a[l + 1][0]);
}
}
cout << ans;
return 0;
}
法二:
利用bitset,显然可以对每一种值开一个bitset。先对序列排序,然后利用 bitset 的 ._Find_first 来找到最小的 \(w_j\)。
可是空间复杂度 \(O(\frac{n^2m}{w})\),怎么办?由于很多 bitset 只存了几个位置,所以根号分治,只存出现次数大于 \(B\) 的,其余在查询时暴力添加。
点击查看代码
// LUOGU_RID: 171446204
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 1e5 + 3, B = 700;
int n, m, k = 0, w[MAXN*5];
map<int, int> mp;
array<int, 6> a[MAXN];
bitset<MAXN> st[MAXN*5/B+3], V, now;
vector<int> _st[MAXN*5];
int main(){
cin >> n >> m;
vector<int> p;
vector<PII> _p;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
cin >> a[i][j], p.push_back(a[i][j]);
}
cin >> a[i][0];
}
////////////////////////////////////////////////////////////////////
sort(a + 1, a + 1 + n), sort(p.begin(), p.end());
for(int i = 0, la = 0; i < p.size(); i++){
if(i == p.size() - 1 || p[i] != p[i + 1]) _p.push_back({i - la + 1, p[i]}), la = i + 1;
}
sort(_p.begin(), _p.end(), [](PII x, PII y){ return x > y; });
for(int i = 0; i < _p.size(); i++){
w[++k] = _p[i].first, mp[_p[i].second] = k;
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++) a[i][j] = mp[a[i][j]];
}
///////////////////////////////////////////////////////////////////
for(int i = 1; i <= n; i++){
V.set(i);
for(int j = 1; j <= m; j++){
if(w[a[i][j]] > B){
st[a[i][j]].set(i);
}else{
_st[a[i][j]].push_back(i);
}
}
}
///////////////////////////////////////////////////////////////////
int ans = 2e9 + 1;
for(int i = 1; i <= n; i++){
now.reset();
for(int j = 1; j <= m; j++){
if(w[a[i][j]] > B){
now |= st[a[i][j]];
}else{
for(int x : _st[a[i][j]]) now.set(x);
}
}
now ^= V;
now.set(0);
int x = now._Find_next(0);
if(x < i) ans = min(ans, a[i][0] + a[x][0]);
}
if(ans > 2e9) ans = -1;
cout << ans;
return 0;
}
P3978 [TJOI2015] 概率论
我们有大小 \(n\) 的二叉树叶子总和等于大小 \(n-1\) 的二叉树个数
证明:
- 设大小 \(n\) 的叶子总数是 \(k\),则可以通过 \(k\) 种删除叶子节点的方法得到多个大小 \(n-1\) 的二叉树(可能有重)
- 而大小 \(n-1\) 的每颗二叉树都有 \(2*(n-1)-(n-2) = n\) 个叶子可以添加,所以通过删除叶子节点得到的二叉树总数(即叶子总数) 等于 \(n\) 倍的 \(n-1\) 大小二叉树总数
大小为 \(n\) 的二叉树个数为卡特兰数,具体见这里,然后就简单了......
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
long double n;
int main(){
cin >> n;
// C(n) = 2n! / n! / (n+1)!
// ans = nC(n-1) / C(n)
// = n * (2n-2)! / (n-1)! / n! / (2n)! * n! * (n+1)!
// = n * (2n-2)! / (n-1)! / (2n)! * (n+1)!
// = n * (2n-2)! / (2n)! * n * (n+1)
// = n * n * (n+1) / 2n / (2n-1)
// = n * (n+1) / 2 / (2n-1)
cout << fixed << setprecision(10);
cout << n / (2.0*n-1.0) * (n+1.0) / 2.0;
return 0;
}
AGC066C - Delete AAB or BAA
设 \(f_i\) 表示前 \(i\) 个字符最少消成剩余多少字符,我们需要找到每个能被删完的区间 \([l,i]\) 或从 \(f_{i-1}\) 转移而来。可是这种 dp 为何正确?若这 dp 不正确,则意味着存在嵌套操作将 dp 的转移操作嵌套了,但是这种区间也是可以删除的,被其它转移包含了。
问题转换为如何判断第一层就嵌套的字符串能否删除。必须满足两个条件:
A的个数是B的个数的两倍- \(s_l \ne s_r\)
如何证明其正确性?
- 设
B的个数为 \(n\)。 - 由于左右端点不同,删除左右两边字符,则剩余 \(n - 1\) 个
B和 \(2n - 1\) 个A - 根据鸽巢原理,即抽屉原理。视作有 \(n\) 个空隙,填充
A后,必然一个 \(B\) 的左右侧有连续 \(2\) 个 'A' - 删除一个
AAB或BAA后转化为子问题,证毕。
用桶优化 dp,时间复杂度线性。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 4e6 + 3;
const int P = 2e6 + 3;
int n;
int dp[MAXN], t[2][MAXN];
string s;
void work(){
cin >> s, n = s.size(), s = " " + s;
vector<int> rc;
rc.push_back(P);
t[(s[1] == 'A' ? 0 : 1)][P] = 0;
for(int i = 1, w = P; i <= n; i++){
int op = (s[i] == 'A' ? 0 : 1);
w += (op == 0 ? 1 : -2), rc.push_back(w);
dp[i] = min(t[op ^ 1][w], dp[i - 1] + 1);
if(i < n){
int _op = (s[i + 1] == 'A' ? 0 : 1);
t[_op][w] = min(t[_op][w], dp[i]);
}
}
cout << (n - dp[n]) / 3 << "\n";
for(int x : rc) t[0][x] = t[1][x] = 1e9;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
for(int i = 0; i <= 4e6; i++) t[0][i] = 1e9, t[1][i] = 1e9;
int T; cin >> T;
while(T--) work();
return 0;
}
/*
1
BAAAAABBA
*/
CF367C - Sereja and the Arrangement of Numbers
问题显然可以通过排序转化为,快速求使 \(1\) 到 \(i\) 数字任意两个数字都相邻过,所需要的最短序列。
考虑建图,一个完全图,我们需要新建边使得 存在欧拉路径(欧拉回路)。
我们显然是有答案的下限 \(\frac{i(i -1)}{2}\),若有 \(i\) 是奇数,则每个 \(i\) 的度数为偶数,存在欧拉回路,答案为 \(\frac{i(i -1)}{2}\)(等于答案下限,必然最优)
若 \(i\) 为偶数,则每个奇数度点之间相消,为 \(\left\lceil\dfrac{i - 2}{2}\right\rceil\)(可以省略两个点,即欧拉路径的起点和终点)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 2e6 + 3;
int n, m;
LL w[MAXN];
int main(){
cin >> n >> m;
for(int i = 1, x; i <= m; i++){
cin >> x >> w[i];
}
sort(w + 1, w + 1 + m, [](int i, int j){ return i > j; });
LL sum = 0, ans = 0;
for(int i = 1; i <= m; i++){
if(i % 2 == 1){
sum = 1 + 1ll * i * (i - 1) / 2;
}else{
sum = 1 + 1ll * i * (i - 1) / 2 + (i - 2 + 1) / 2;
}
if(sum > n) break;
ans += w[i];
}
cout << ans;
return 0;
}
CF1186F - Vus the Cossack and a Graph
考虑欧拉回路构造,如果所有点的度数为偶数,即存在欧拉回路,那么我们可以得到一个边的序列,按一选一不选的方式。这显然可以满足 \(i\) 点度数大于等于 \(\left\lceil\dfrac{d_i}{2}\right\rceil\),至于另外一个限制,我们只选择了 \(\left\lceil\dfrac{m}{2}\right\rceil\) 个,也满足。
如果存在度数为奇数的边,两两配对连边,则最多建 \(\left\lfloor\dfrac{n}{2}\right\rfloor\) 条虚边(注意度数为奇数的点个数为偶数)。然后得到欧拉回路后就不选虚边,其它同样,第一点显然满足,如何证明满足第二点?
显然不能大于这个值:\(\left\lceil\dfrac{m}{2}\right\rceil + \left\lfloor\dfrac{n}{2}\right\rfloor\),然后就没了
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 2e6 + 3;
int n, m, d[MAXN];
vector<PII> eg[MAXN];
vector<PII> ans;
bool vis[MAXN];
void dfs(int x, int op){
while(!eg[x].empty()){
PII e = eg[x].back();
eg[x].pop_back();
if(vis[e.second]) continue;
vis[e.second] = 1;
dfs(e.first, e.second > m);
}
ans.push_back({x, op});
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
for(int i = 1, U, V; i <= m; i++){
cin >> U >> V, d[U]++, d[V]++, eg[V].push_back({U, i}), eg[U].push_back({V, i});
}
vector<int> p;
for(int i = 1; i <= n; i++){
if(d[i] & 1) p.push_back(i);
}
for(int i = 0, cnt = m; i < p.size(); i += 2){
cnt++;
eg[p[i]].push_back({p[i + 1], cnt}), eg[p[i + 1]].push_back({p[i], cnt});
}
vector<PII> ANS;
for(int i = 1; i <= n; i++){
if(eg[i].empty()) continue;
ans.clear(), dfs(i, 0);
reverse(ans.begin(), ans.end());
//for(int i = ans.size() - 1; i >= 1; i--) ans[i].second = ans[i - 1].second;
for(int i = 1, ooo = 1; i < ans.size(); i++){
if(ans[i].second == 1) continue;
if((i == 1 ? ans.back().second : ans[i - 1].second) == 1
|| (i == ans.size() - 1 ? ans[1].second : ans[i + 1].second)
|| ooo){
ANS.push_back({ans[i - 1].first, ans[i].first}), ooo = 0;
}else{
ooo = 1;
}
}
}
cout << ANS.size() << "\n";
for(PII e : ANS) cout << e.first << " " << e.second << "\n";
return 0;
}
P4980 【模板】Polya 定理
根据 Burnside 定理 可以转化为,一个图,\(nxt_i = (i + k) \bmod n\),求图中有多少环。
设一个环长 \(a\),则 \(ak \bmod n = 0\),解得 \(a = \dfrac{n}{\gcd(n, k)}\),所以环的个数为 \(\dfrac{n}{a}\),即 \(\gcd(k, n)\)
CF1946F - Nobody is needed
注意这题不能从左向右扫描线!!!所以所有扫描线不一定随意方向
从右向左扫描线,我们需要添加 \(i\) 为子序列开头的子序列个数。可以 dp,枚举 \(a_i\) 的倍数,再枚举倍数的倍数,转移,正确性显然,复杂度在排列的限制下为 \(O(\log n \log n)\)。
现在你再来思考一下能不能从左向右扫描线。。。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 1e6 + 3;
int n, Q;
int a[MAXN], b[MAXN];
vector<PII> q[MAXN];
LL sum[MAXN], dp[MAXN];
LL ans[MAXN];
void ADD(int x, LL w){
for(; x <= n; x += (x & (-x))) sum[x] += w;
}
LL QUE(int x){
LL ret = 0;
for(; x >= 1; x -= (x & (-x))) ret += sum[x];
return ret;
}
void work(){
cin >> n >> Q;
for(int i = 1; i <= n; i++) dp[i] = 0, sum[i] = 0, q[i].clear();
for(int i = 1; i <= n; i++){
cin >> a[i], b[a[i]] = i;
}
for(int i = 1, l, r; i <= Q; i++){
cin >> l >> r;
q[l].push_back({r, i});
}
for(int i = n; i >= 1; i--){
dp[a[i]] = 1;
for(int j = a[i]; j <= n; j += a[i]){
if(b[j] >= i){
for(int h = j + j; h <= n; h += j){
if(b[h] >= b[j]) dp[h] += dp[j];
}
ADD(b[j], dp[j]);
dp[j] = 0;
}
}
for(PII x : q[i]){
ans[x.second] = QUE(x.first);
}
}
for(int i = 1; i <= Q; i++) cout << ans[i] << " ";
cout << "\n";
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
int T;
cin >> T;
while(T--) work();
return 0;
}
/*
1
3 1
3 2 1
1 2
2
*/
[ARC176E] Max Vector
对于这种要么...要么...的题目,可以考虑考虑最小割。
开 \(2n\) 条链,链从大走到小,然后连限制。
luogu - P10997 【MX-J3-T4】Partition
首先需要化简题面(可以自己猜,然后证明)。具体见官方题解。
然后注意两条分割线在贪心的情况下是互相独立的,可以分别求。
CF993E - Nikita and Order Statistics
显然可以化简为问多少对 \((i,j)\) 满足 \(s_i - s_j = k\),然后注意!!!\(s_i\) 和 \(s_j\) 是互相独立的,所以对于每个 \(k\),统计满足 \(i - j = k\) 的 \(f[i]\times f[j]\) 的和(\(f[j]\) 表示 \(j\) 在 \(s\) 数组中的出现次数) ,其中 \(k = 0\) 需要单独统计。
然后就可以 FFT 优化了(翻转 \(f\)),则限制变为 \(i - (n - j) = k\),得 \(i + j = k + n\)
CF776D - The Door Problem
注意到题目给了每个点最多被两个钥匙控制,所以两个钥匙的状态是固定的,我们可以给每个钥匙建两个节点,表示两种状态(选和不选),然后建边加限制,可以利用并查集。
luogu - P10641 BZOJ3252 攻略
考虑一个朴素的贪心:每次选择一个到根路径价值和最大的叶子,将价值和累加进答案,并把这条链价值清零。
这个贪心的正确性显然,但是数据结构实现有些复杂,考虑优化。
发现不断选择长链等价于这个贪心。
- 每条长链的终点为叶子。
- 长链的最上面的端点,一定在之前选的链包含了。
- 长链的长度一定最长
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 2e5 + 3;
int n, k, son[MAXN];
LL dep[MAXN], w[MAXN];
vector<LL> vt;
vector<int> eg[MAXN];
void dfs(int x, int dad){
for(int nxt : eg[x]){
if(nxt == dad) continue;
dfs(nxt, x);
if(!son[x] || dep[son[x]] < dep[nxt]) son[x] = nxt;
}
dep[x] = dep[son[x]] + w[x];
for(int nxt : eg[x]){
if(nxt != dad && nxt != son[x]) vt.push_back(dep[nxt]);
}
}
int main(){
cin >> n >> k;
for(int i = 1; i <= n; i++){
cin >> w[i];
}
for(int i = 1, U, V; i < n; i++){
cin >> U >> V;
eg[U].push_back(V), eg[V].push_back(U);
}
dfs(1, 0);
vt.push_back(dep[1]);
sort(vt.begin(), vt.end());
LL ans = 0;
while(k--){
if(vt.empty()) break;
ans += vt.back(), vt.pop_back();
}
cout << ans;
return 0;
}
CF1709F - Multiset of Strings
先要要从 01-Trie 的角度思考,那么问题转化为流量问题,要求给每条边一条流量限制。
然后就有 dp 式子了,具体见:https://www.luogu.com.cn/article/xz491sc5
P10668 BZOJ2720 [Violet 5] 列队春游
由于期望可以加和,所以将期望分解,变为求每个人期望值。
设小于 \(h_i\) 的人的个数为 \(s\),除去 \(s\) 个人-,有 \(n - s + 1\) 个空位可以插入 \(s\) 个人。然后注意到 \(i\) 这个人的位置不用具体确定,因为无论 \(i\) 在哪里,期望都相同,所以不用管。每个人贡献的期望为 \(1 \times \dfrac{1}{n - s + 1}\),最后总期望为 \(1 \times \dfrac{s}{n - s + 1}\)
GCDEX - GCD Extreme
有多组数据且很大,平常的求解是行不通了,我们为了预处理,考虑前缀和。
设 \(ans(n) = ans(n - 1) + \sum\limits_{i=1}^{n-1}{\gcd(i, n)}\),对于后面的部分可以照常推式子。
注意枚举 \(1\) 到 \(n\) 的每个数的每个约数,可以调和级数复杂度(类似埃氏筛的写法)。
luogu - P4690 [Ynoi2016] 镜中的昆虫
初步感觉没法直接做,感觉区间赋值没有利用很可惜。
考虑维护 \(pre\) 数组(常见套路,前面第一个等于 \(i\) 的位置,没有则为 \(0\))注意到区间赋值会使得一些 \(pre_i\) 变为 \(i-1\)。先写一个暴力,利用 珂朵莉树 和 CQD 分治解决,然后发现过了???
结论:最多有 \(O(n+m)\) 个 \(pre_i\) 进行修改。
证明:
- 将一段连续颜色视作一块,那么每次操作会合并很多块,并且最多新建 \(3\) 个块(左右新建,中间新建)
- 块的个数是少的,因为每次需要维护的是块头,所以复杂度正确。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
mt19937 rnd(time(0));
int ssss = 0;
map<int, int> mmpp;
int read(){ // 离散化
int x; cin >> x;
if(mmpp.find(x) != mmpp.end()) return mmpp[x];
return mmpp[x] = ++ssss;
}
const int MAXN = 1e5 + 3, MAXK = 5e6 + 3;
struct Ask{
int op, _op, r, w1, w2, id;
}q[MAXK];
struct Node{
int l, r, w;
bool operator< (Node j) const {
return l == j.l ? r < j.r : l < j.l;
}
};
set<Node> st;
int n, m, k = 0, _k = 0, a[MAXN], pre[MAXN], lt[MAXN];
set<Node> S[MAXN * 2];
int ANS[MAXN];
inline auto Erase(auto it){
S[it->w].erase({it->l, it->r, 0});
return st.erase(it);
}
inline auto Insert(Node x){
S[x.w].insert({x.l, x.r, 0});
return st.insert(x).first;
}
auto split(int pos){
if(pos > n) return st.end();
auto it = st.lower_bound({pos, 0, 0});
if(it != st.end() && it->l == pos) return it;
it--;
Node x = *it;
Erase(it), Insert({x.l, pos - 1, x.w});
return Insert({pos, x.r, x.w});
}
int Find(int x, int w){
auto it = S[w].lower_bound({x, 0, 0});
if(it == S[w].begin()) return 0;
return min(x - 1, prev(it)->r);
}
void AddQ(int x, int _pre){
q[lt[x]] = {0, 1, k, x, pre[x], 0};
k++, q[k] = {0, -1, lt[x] - 1, x, pre[x], 0};
pre[x] = _pre, lt[x] = ++k;
}
int sum[MAXN];
void Solve(int l, int r){
if(r == l){
return;
}
int mid = (l + r) >> 1;
Solve(l, mid), Solve(mid + 1, r);
sort(q + l, q + mid + 1, [](Ask i, Ask j){ return i.w1 < j.w1; });
sort(q + mid + 1, q + r + 1, [](Ask i, Ask j){ return i.w1 < j.w1; });
int cc = 0;
for(int j = l, i = mid + 1; i <= r; i++){
while(j <= mid && q[j].w1 <= q[i].w1){
cc += q[j].op == 0;
if(q[j].op == 0) for(int x = q[j].w2 + 1; x <= n + 1; x += (x & (-x))) sum[x] += q[j]._op;
j++;
}
if(q[i].op == 0) continue;
int ret = 0;
for(int x = q[i].w2 + 1; x >= 1; x -= (x & (-x))) ret += sum[x];
ANS[q[i].id] += q[i]._op * ret;
}
for(int j = l; j <= mid; j++){
if(q[j].op == 0) for(int x = q[j].w2 + 1; x <= n + 1; x += (x & (-x))) sum[x] = 0;
}
}
/*
5 1
1 2 3 4 5
2 1 5
*/
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; i++){
a[i] = read(), S[a[i]].insert({i, i, 0}), st.insert({i, i, a[i]});
pre[i] = Find(i, a[i]), lt[i] = ++k;
}
for(int qq = 1, l, r, op, x; qq <= m; qq++){
cin >> op >> l >> r;
//op = rnd() % 2 + 1, l = rnd() % n + 1, r = rnd() % n + 1;
if(l > r) swap(l, r);
if(op == 1){
x = read();
auto ir = split(r + 1), il = split(l);
auto _it = next(il);
vector<PII> vt;
auto ___it = st.lower_bound({il->l, 0, 0});
vt.push_back({___it->w, l});
Erase(il); //////////////
AddQ(l, Find(l, x));
vt.push_back({x, r});
for(auto it = _it; it != st.end() && it != ir; it = st.erase(it)){
S[it->w].erase({it->l, it->r, 0});
AddQ(it->l, it->l - 1), vt.push_back({it->w, it->l});
}
sort(vt.begin(), vt.end());
Insert({l, r, x});
for(int i = 0; i < vt.size(); i++){
if(i == vt.size() - 1 || vt[i].first != vt[i + 1].first){
int w = vt[i].first;
auto it = S[w].lower_bound({r + 1, 0, 0});
if(it != S[w].end()){
auto __it = st.lower_bound({it->l, 0, 0}); ///////////////
AddQ(it->l, Find(it->l, __it->w));
}
}
}
}else{
k++, _k++;
q[k] = {1, 1, k, r, l - 1, _k};
k++;
q[k] = {1, -1, k, l - 1, l - 1, _k};
}
}
for(int i = 1; i <= n; i++){
auto it = st.lower_bound({i + 1, 0, 0});
pre[i] = Find(i, prev(it)->w);
AddQ(i, 0);
}
sort(q + 1, q + 1 + k, [](Ask i, Ask j){ return i.r == j.r ? i.op < j.op : i.r > j.r; });
/*
cout << k << " &&\n";
for(int i = 1; i <= k; i++){
cout << i << " " << q[i].op << " " << q[i]._op << " " << q[i].r << " " << q[i].w1 << " " << q[i].w2 << " " << q[i].id << "\n";
}
*/
Solve(1, k);
for(int i = 1; i <= _k; i++) cout << ANS[i] << "\n";
return 0;
}
/*
10 2
5 9 7 5 4 2 9 1 4 9
1 3 9 3
2 7 10
ans: 2
10 5
5 4 9 2 3 3 6 5 4 2
1 6 7 2
1 3 6 1
1 8 9 1
1 8 9 1
2 4 10
ans: 2
10 4
4 8 6 6 1 1 7 10 2 9
1 5 8 2
2 1 9
1 5 9 5
1 1 6 4
ans: 4
10 3
4 6 3 7 2 5 9 8 2 7
1 2 3 8
2 1 7
1 5 9 8
ans: 6
10 4
46 74 99 82 52 79 82 1 81 52
1 1 8 83
1 1 3 35
2 7 9
1 5 7 24
ans: 2
2 0 1 50 9 0 0
3 0 1 48 8 4 0
4 0 1 46 7 6 0
5 0 1 44 6 5 0
7 0 1 40 4 0 0
8 0 1 38 3 2 0
9 0 1 36 2 1 0
10 0 1 34 1 0 0
12 0 1 32 5 4 0
*/
[ABC365F] Takahashi on Grid
考虑贪心:
- 能向下走就向下走
- 在交集中就直接走,不在交集就走到交集
考虑线段树,那么我们需要考虑一段区间,可以注意到,如果所有区间的交集为空,则必定存在起点和终点,满足一定不劣。
然后就根据这个分类讨论 线段树合并。有些细节要注意,具体看代码......
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 2e5 + 3;
struct SgT{
int in, out;
LL sum;
int l, r;
}tr[MAXN * 4];
int dl[MAXN], dr[MAXN];
SgT Merge(SgT i, SgT j){
SgT ret;
ret.l = max(i.l, j.l), ret.r = min(i.r, j.r), ret.sum = i.sum + j.sum;
if(i.l > i.r && j.l > j.r){
ret.in = i.in, ret.out = j.out;
ret.sum += abs(i.out - j.in);
}else if(i.l > i.r){
ret.in = i.in;
if(i.out < j.l) ret.sum += abs(i.out - j.l), ret.out = j.l;
else if(i.out > j.r) ret.sum += abs(i.out - j.r), ret.out = j.r;
else ret.out = i.out;
}else if(j.l > j.r){
ret.out = j.out;
if(i.r < j.in) ret.sum += abs(i.r - j.in), ret.in = i.r;
else if(j.in < i.l) ret.sum += abs(j.in - i.l), ret.in = i.l;
else ret.in = j.in;
}else if(ret.l > ret.r){
if(i.r < j.l) ret.sum += abs(i.r - j.l), ret.in = i.r, ret.out = j.l;
else if(j.r < i.l) ret.sum += abs(i.l - j.r), ret.in = i.l, ret.out = j.r;
}
return ret;
}
void Build(int i, int l, int r){
if(l == r){
tr[i].l = dl[l], tr[i].r = dr[l];
return;
}
int mid = (l + r) >> 1;
Build(i * 2, l, mid), Build(i * 2 + 1, mid + 1, r);
tr[i] = Merge(tr[i * 2], tr[i * 2 + 1]);
}
SgT ret;
void Query(int i, int l, int r, int L, int R){
if(l == L && r == R){
if(ret.in == -1){
ret = tr[i];
}else ret = Merge(ret, tr[i]);
return;
}
int mid = (l + r) >> 1;
if(L <= mid) Query(i * 2, l, mid, L, min(mid, R));
if(mid + 1 <= R) Query(i * 2 + 1, mid + 1, r, max(mid + 1, L), R);
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
int n;
cin >> n;
for(int i = 1; i <= n; i++){
cin >> dl[i] >> dr[i];
}
Build(1, 1, n);
int Q;
cin >> Q;
for(int q = 1, l, r, x, y; q <= Q; q++){
cin >> l >> x >> r >> y;
if(l > r) swap(l, r), swap(x, y);
ret = {-1, 0, 0, 0, 0}, Query(1, 1, n, l, r);
LL ans = r - l;
if(ret.l > ret.r){
ans += ret.sum + abs(x - ret.in) + abs(y - ret.out);
}else{
if(x < ret.l) ans += abs(ret.l - x) + abs(ret.l - y);
else if(x > ret.r) ans += abs(ret.r - x) + abs(ret.r - y);
else ans += abs(x - y);
}
cout << ans << "\n";
}
return 0;
}
luogu - P2257 YY的GCD
参考题解:https://www.luogu.com.cn/article/djqcjqtk
重要的是推到 \(\sum\limits_{k\in Prime}{\sum\limits_{d=1}^{n/k}{\mu(d) \left\lfloor\frac{n}{kd}\right\rfloor \left\lfloor\frac{m}{kd}\right\rfloor}}\) 后,需要想到换元法 \(T = kd\)
得到 \(\sum\limits_{T=1}^{n}{\sum\limits_{k|T, k\in P}{\mu(\frac{T}{k}) \left\lfloor\frac{n}{T}\right\rfloor \left\lfloor\frac{m}{T}\right\rfloor}}\) 即 \(\sum\limits_{T=1}^{n}{\left\lfloor\frac{n}{T}\right\rfloor \left\lfloor\frac{m}{T}\right\rfloor\sum\limits_{k|T, k\in P}{\mu(\frac{T}{k}) }}\),然后发现可以前缀和预处理+数论分块。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e7 + 3;
int vis[MAXN];
LL sum[MAXN], mu[MAXN];
int main(){
ios::sync_with_stdio(0), cin.tie(0);
for(int i = 1; i <= 1e7; i++) mu[i] = 1;
for(int i = 2; i <= 1e7; i++){
if(vis[i]) continue;
for(int j = i; j <= 1e7; j += i){
vis[j] = 1, mu[j] *= -1;
if(j % LL(i * i) == 0) mu[j] = 0;
}
}
for(int i = 1; i <= 1e7; i++) vis[i] = 0;
for(int i = 2; i <= 1e7; i++){
if(vis[i]) continue;
for(int j = i; j <= 1e7; j += i){
vis[j] = 1, sum[j] += mu[j / i];
}
}
for(int i = 1; i <= 1e7; i++) sum[i] += sum[i - 1];
int T, n, m;
cin >> T;
while(T--){
cin >> n >> m;
if(n > m) swap(n, m);
LL ans = 0;
for(int l = 1, r; l <= n; l = r + 1){
r = min(n / (n / l), m / (m / l));
ans += LL(n / r) * LL(m / r) * (sum[r] - sum[l - 1]);
}
cout << ans << "\n";
}
return 0;
}
MX - 人口局 DBA
题面
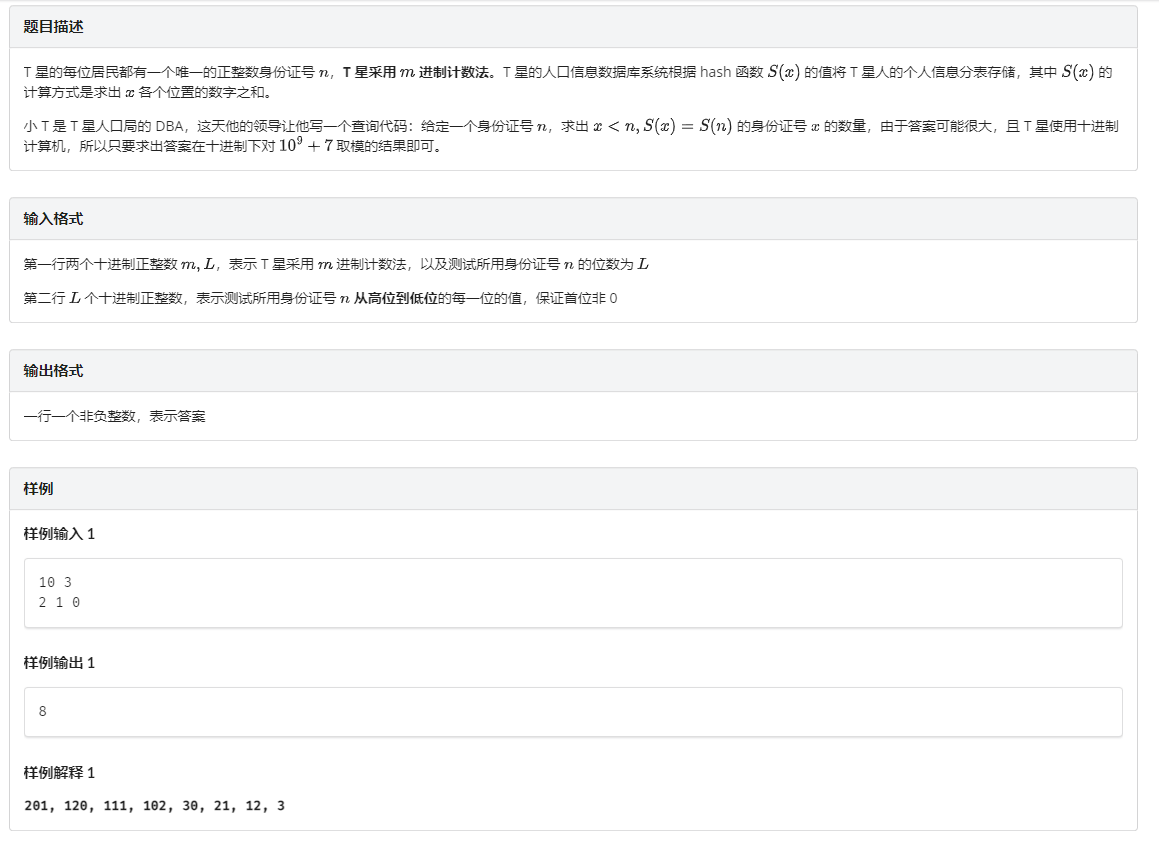

对于求 \(\sum\limits_{i=1}^{n}{a_i} = s\) 且 \(0 \le a_i \le m\) 的解的个数,常见方法是容斥,枚举有多少个大于 \(m\) 的,则答案为 \(\sum\limits_{k=0}^{n}{(-1)^k \dbinom{n}{k} \dbinom{s - km + n - 1}{m + n - 1}}\)。
然后推到公式。
具体见:https://www.luogu.com.cn/paste/qk8atw8v
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 2000 + 3, MAXV = 4e6 + 3, V = 4e6;
const LL mod = 1e9 + 7;
LL qpow(LL A, LL B){
LL ret = 1;
while(B > 0){
if(B & 1) ret = ret * A % mod;
A = A * A % mod, B >>= 1;
}
return ret;
}
int m, n, a[MAXN], sum = 0;
LL fac[MAXV], ifac[MAXV];
LL C(int A, int B){
if(A > B) return 0;
return fac[B] * ifac[A] % mod * ifac[B - A] % mod;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> m >> n;
for(int i = 1; i <= n; i++){
cin >> a[i];
sum += a[i];
}
fac[0] = 1;
for(int i = 1; i <= V; i++) fac[i] = fac[i - 1] * i % mod;
ifac[V] = qpow(fac[V], mod - 2);
for(int i = V - 1; i >= 0; i--) ifac[i] = ifac[i + 1] * (i + 1) % mod;
LL ans = 0;
for(int i = 1; i < n; i++){
int op = 1, l = n - i + 1;
for(int k = 0; k < l; k++){
if(k * m > sum) break;
ans = (ans + (op == 1 ? 1 : mod - 1) * C(k, l - 1) % mod
* ((C(l - 1, sum - k * m + l - 1) - C(l - 1, sum - a[i] - k * m + l - 1) + mod) % mod) % mod) % mod;
op *= -1;
}
sum -= a[i];
}
cout << ans;
return 0;
}
MX - 银行的源起
题面
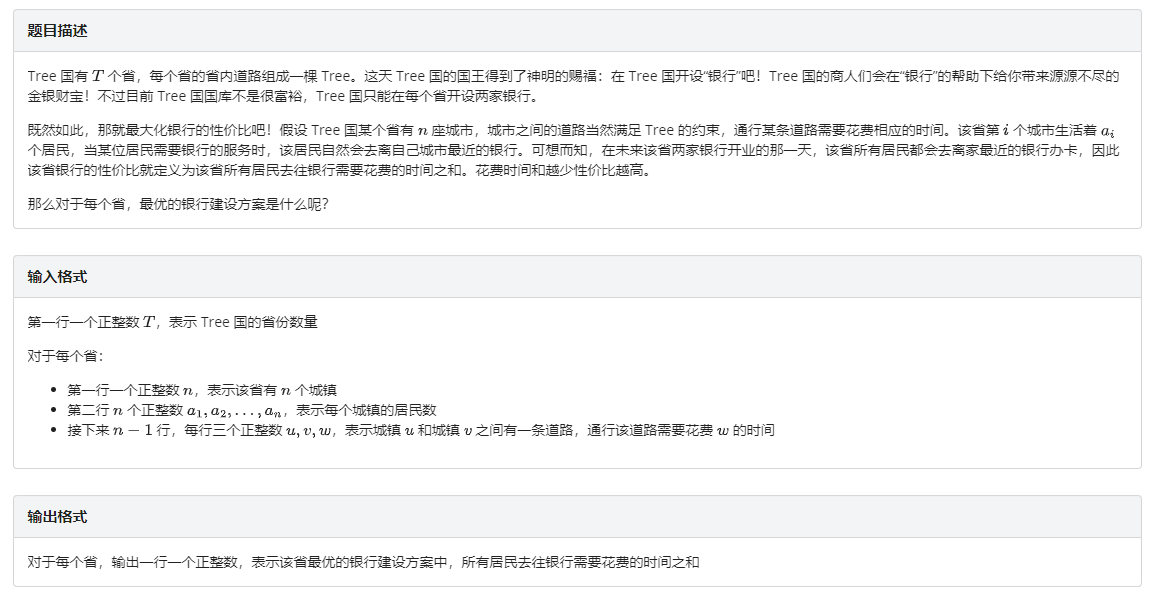
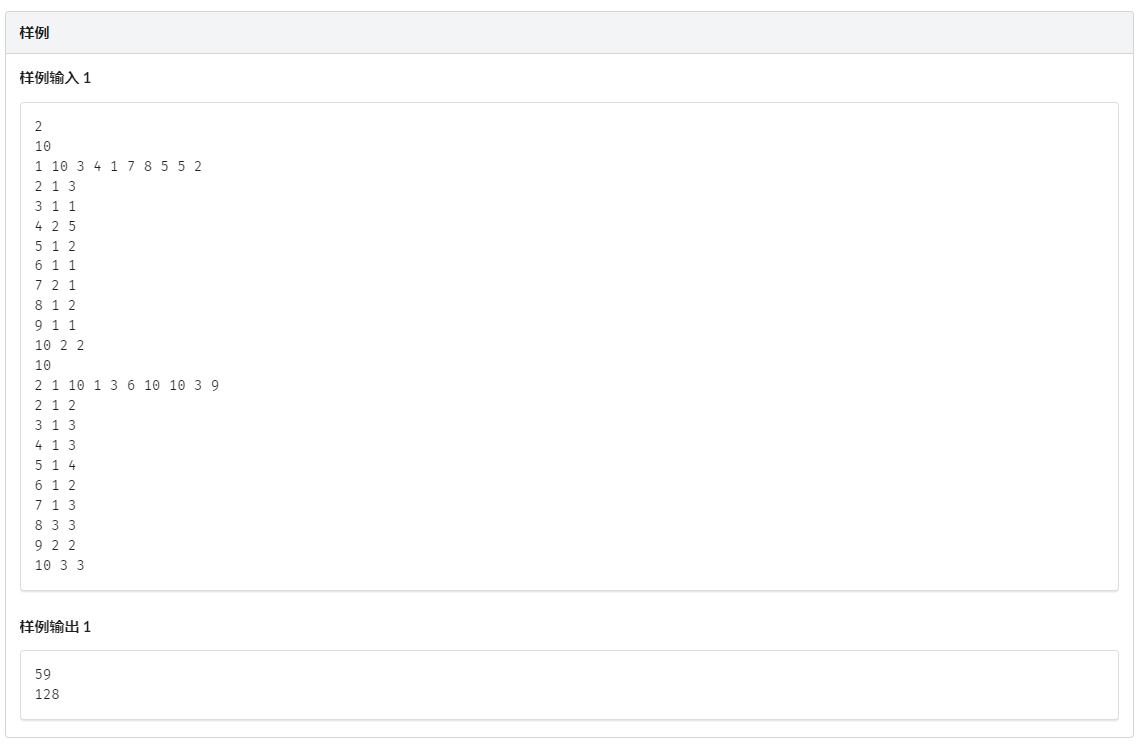

整体做法:求出断每条边后的两个重心,然后统计答案。
对于求每个子树的重心:
- 一棵子树的重心,一定是重儿子的重心向上跳。实现可以暴力,复杂度 \(O(n)\)
对于求每个子树外部的重心:
- 首先以全树的重心作为根,再考虑从父亲到儿子的重心变化。
- 一定是外部重心向根节点跳,倍增实现,复杂度 \(O(n \log n)\)。
统计答案:
- 先换根 dp 求出每个点作为汇点,全树的答案。复杂度 \(O(n)\)。
- 对于求子树外部的答案:
- 先减去某个子树内的答案贡献。
- 再减去两点之间距离
- 倍增实现,复杂度 \(O(n \log n)\).
- 对于求子树内部的答案:
- 方法类似。
- 倍增实现,复杂度 \(O(n \log n)\)
这里有一个另外的一种做法:https://www.luogu.com.cn/paste/qk8atw8v
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 1e5 + 3, MAXL = 19;
int n, root;
LL a[MAXN], ANS[MAXN], ssss = 0;
vector<PII> eg[MAXN];
int focus[MAXN], exfocus[MAXN], anc[MAXL][MAXN];
LL sz[MAXN], mx[MAXN], dp[MAXN], sss[MAXN];
LL dep[MAXN], llen[MAXN], fe[MAXN];
void dfs1(int x, int dad){ // 求全局重心,预处理换根 dp
mx[x] = 0, sz[x] = a[x], dp[x] = 0;
for(PII e : eg[x]){ int nxt = e.first;
if(nxt == dad) continue;
dfs1(nxt, x), mx[x] = max(mx[x], sz[nxt]), sz[x] += sz[nxt];
dp[x] += dp[nxt] + sz[nxt] * e.second;
}
mx[x] = max(mx[x], ssss - sz[x]);
if(!root || mx[x] < mx[root]) root = x;
}
void dfs2(int x, int dad){ // 换根 dp
sss[x] = dp[x];
for(PII e : eg[x]){ int nxt = e.first;
if(nxt == dad) continue;
LL _dpx = dp[x], _dpnx = dp[nxt], _szx = sz[x], _sznx = sz[nxt];
dp[x] -= dp[nxt] + sz[nxt] * e.second;
sz[x] -= sz[nxt];
dp[nxt] += dp[x] + sz[x] * e.second;
sz[nxt] = ssss;
dfs2(nxt, x);
sz[x] = _szx, sz[nxt] = _sznx, dp[x] = _dpx, dp[nxt] = _dpnx;
}
}
void dfs3(int x, int dad){ // 现在开始以 root 为根,求重儿子、子树内重心、倍增数组
anc[0][x] = dad;
focus[x] = 0, sz[x] = a[x], mx[x] = 0, dp[x] = 0; // mx 数组表示重儿子
for(PII e : eg[x]){ int nxt = e.first;
if(nxt == dad) continue;
dep[nxt] = dep[x] + 1, llen[nxt] = llen[x] + e.second, fe[nxt] = e.second;
dfs3(nxt, x), sz[x] += sz[nxt];
dp[x] += dp[nxt] + sz[nxt] * e.second;
if(mx[x] == 0 || sz[nxt] > sz[mx[x]]) mx[x] = nxt;
}
if(!mx[x]){
focus[x] = x;
return;
}
focus[x] = focus[mx[x]];
LL w = max(sz[mx[focus[x]]], sz[x] - sz[focus[x]]);
while(focus[x] != x){
int nx = anc[0][focus[x]];
LL _w = max(sz[mx[nx]], sz[x] - sz[nx]);
if(_w >= w) break;
w = _w, focus[x] = nx;
}
}
LL tmp = 0, _tmp = 0, __tmp = 0, opt = 0;
void dfs4(int x, int dad, int now){
LL Size = ssss - sz[x];
if(opt) tmp = max(_tmp, __tmp - sz[x]);
else tmp = _tmp;
for(int l = MAXL - 1; l >= 0; l--){
if(anc[l][now] > 0 && (anc[l][now] == root ? tmp : sz[mx[anc[l][now]]]) <= Size / 2) now = anc[l][now];
}
exfocus[x] = now;
for(PII e : eg[x]){ int nxt = e.first;
if(nxt != dad) dfs4(nxt, x, now);
}
}
int LCA(int x, int y){
if(dep[x] > dep[y]) swap(x, y);
for(int l = 0, k = dep[y] - dep[x]; l < MAXL; l++){
if((k >> l) & 1) y = anc[l][y];
}
if(x == y) return x;
for(int l = MAXL - 1; l >= 0; l--){
if(anc[l][x] != anc[l][y]) x = anc[l][x], y = anc[l][y];
}
return anc[0][x];
}
void dfs5(){
for(int i = 1; i <= n; i++){
if(i == root) continue;
int x = i, y = exfocus[i], lca = LCA(x, y);
LL len = llen[x] + llen[y] - llen[lca] - llen[lca];
ANS[i] += sss[y] - dp[i] - len * sz[i];
}
}
void dfs6(){
for(int i = 1; i <= n; i++){
if(i == root) continue;
int x = anc[0][i], y = focus[i], lca = LCA(x, y);
LL len = llen[x] + llen[y] - llen[lca] - llen[lca];
ANS[i] += sss[y] - (sss[x] - dp[i] - sz[i] * fe[i]) - len * (sz[root] - sz[i]);
}
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
freopen("banking.in", "r", stdin);
freopen("banking.out", "w", stdout);
int T; cin >> T;
while(T--){
cin >> n;
ssss = 0;
for(int i = 1; i <= n; i++){
cin >> a[i], ssss += a[i], eg[i].clear();
}
for(int i = 1, U, V, W; i < n; i++){
cin >> U >> V >> W;
eg[U].push_back({V, W}), eg[V].push_back({U, W});
}
root = 0, dfs1(1, 0), dfs2(1, 0);
llen[root] = 0, dep[root] = 0, dfs3(root, 0);
for(int l = 1; l < MAXL; l++){
for(int i = 1; i <= n; i++) anc[l][i] = anc[l-1][anc[l-1][i]];
}
vector<int> p;
for(PII e : eg[root]) p.push_back(e.first);
sort(p.begin(), p.end(), [](int i, int j){ return sz[i] > sz[j]; });
for(PII e : eg[root]){ int nxt = e.first;
int now = root;
opt = 0, _tmp = 0;
if(p[0] != nxt){
now = focus[p[0]], opt = 0, _tmp = sz[p[0]];
}else if(p.size() > 1) now = focus[p[1]], __tmp = sz[nxt], _tmp = (p.size() > 1 ? sz[p[1]] : 0), opt = 1;
else now = root, opt = 1, _tmp = 0, __tmp = sz[nxt];
dfs4(nxt, root, now);
}
for(int i = 1; i <= n; i++) ANS[i] = 0;
dfs5(), dfs6();
LL ans = 1e18;
/*
cout << "* " << root << "\n";
for(int i = 1; i <= n; i++){
cout << i << " " << focus[i] << " " << exfocus[i] << "\n";
}
*/
for(int i = 1; i <= n; i++){
if(i != root) ans = min(ans, ANS[i]);
}
cout << ans << "\n";
}
return 0;
}
/*
1
10
10 9 4 2 6 8 7 8 4 4
2 1 1
3 2 8
4 2 1
5 1 3
6 5 3
7 4 6
8 7 7
9 8 8
10 6 5
240
1
5
2 2 2 2 1
2 1 5
3 1 5
4 1 1
5 4 2
15
1
5
3 4 2 4 2
2 1 1
3 1 1
4 1 4
5 4 4
14
*/
[ABC304G] Max of Medians
求中位数最值的常见方法就是二分中位数,然后判断大于的个数。
在 01-Trie 上考虑,则若 \(x\) 和 \(y\) 都相同是一种走法,\(x\) 和 \(y\) 不同是另外一种走法,具体实现就是分类讨论,可以看代码辅助理解。
点击查看代码
// LUOGU_RID: 176069415
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 2e5 + 3;
int tot = 1, eg[MAXN * 31][2], cnt[MAXN * 31];
int n, a[MAXN];
int _Solve(int bit, int x, int y, int k){
if(!x || !y) return 0;
if(bit < 0) return min(cnt[x], cnt[y]);
int col = (k >> bit) & 1;
int ret = 0;
if(!col){
int A = cnt[eg[x][0]], B = cnt[eg[x][1]], C = cnt[eg[y][0]], D = cnt[eg[y][1]];
if(A > D && C > B){
return B + D + min({A - D, C - B, _Solve(bit - 1, eg[x][0], eg[y][0], k)});
}else if(A < D && C < B){
return A + C + min({D - A, B - C, _Solve(bit - 1, eg[x][1], eg[y][1], k)});
}else{
return min(A, D) + min(C, B);
}
}else{
return _Solve(bit - 1, eg[x][0], eg[y][1], k) + _Solve(bit - 1, eg[x][1], eg[y][0], k);
}
}
int Solve(int bit, int x, int k){
if(!x || bit < 0) return 0;
int col = (k >> bit) & 1;
int ret = 0;
if(!col){
int A = cnt[eg[x][0]], B = cnt[eg[x][1]];
if(A > B){
ret += min((A - B) / 2, Solve(bit - 1, eg[x][0], k)) + B;
}else{
ret += min((B - A) / 2, Solve(bit - 1, eg[x][1], k)) + A;
}
}else{
return _Solve(bit - 1, eg[x][0], eg[x][1], k);
}
return ret;
}
bool check(int k){
return Solve(29, 1, k) >= n - (n / 2);
}
int main(){
cin >> n;
for(int i = 1, x; i <= 2 * n; i++){
cin >> x, a[i] = x;
int p = 1;
for(int bit = 29; bit >= 0; bit--){
int col = (x >> bit) & 1;
if(!eg[p][col]) eg[p][col] = ++tot;
p = eg[p][col], cnt[p]++;
}
}
int l = 0, r = (1ll << 30) - 1;
while(l < r){
int mid = (l + r + 1) >> 1;
if(check(mid)){
l = mid;
}else r = mid - 1;
}
cout << l;
return 0;
}
[ABC304Ex] Constrained Topological Sort
贪心好题。
若 \(m=0\),则是一个常见的贪心。
考虑加上边的限制,我们考虑给每个点的 \(l,r\) 进行修改,是的贪心得到的答案满足拓扑序。
对于有向边 \((x,y)\),为了优先 \(x\),则 \(l_y = \max(l_y, l_x + 1)\),同时如果 \(l_x\) 被其他选了,则还需要有先 \(x\),则 \(r_x = \min(r_x, r_y - 1)\),这样贪心的结果必定是满足拓扑序的,那正确性呢?
正确性:若\([l_x,r_x]\) 与 \([l_y,r_y]\) 的交初始不满,则显然正确,否则,交集大小减一,任然正确。
注意:可能在修改 \(l_y\) 之前 \(l_x\) 需要进行修改,所以需要在拓扑排序上进行修改( \(r\) 就在反图上拓扑排序)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 4e5 + 3;
struct Node{
int l, r, id;
}a[MAXN];
int n, m, ans[MAXN];
vector<PII> q[MAXN];
int d[MAXN], _d[MAXN];
vector<int> _eg[MAXN], eg[MAXN];
void No(){
cout << "No";
exit(0);
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
for(int i = 1, U, V; i <= m; i++){
cin >> U >> V;
eg[U].push_back(V), d[V]++;
_eg[V].push_back(U), _d[U]++;
}
for(int i = 1; i <= n; i++){
cin >> a[i].l >> a[i].r, a[i].id = i;
}
vector<int> stk;
for(int i = 1; i <= n; i++){
if(!d[i]) stk.push_back(i);
}
while(!stk.empty()){
int i = stk.back();
stk.pop_back();
for(int nxt : eg[i]){
d[nxt]--, a[nxt].l = max(a[nxt].l, a[i].l + 1);
if(!d[nxt]) stk.push_back(nxt);
}
}
for(int i = 1; i <= n; i++){
if(d[i]) No();
}
stk.clear();
for(int i = 1; i <= n; i++){
if(!_d[i]) stk.push_back(i);
}
while(!stk.empty()){
int i = stk.back();
stk.pop_back();
for(int nxt : _eg[i]){
_d[nxt]--, a[nxt].r = min(a[nxt].r, a[i].r - 1);
if(!_d[nxt]) stk.push_back(nxt);
}
}
for(int i = 1; i <= n; i++){
if(a[i].l > n || a[i].l < 1 || a[i].r < a[i].l) No();
q[a[i].l].push_back({a[i].r, i});
}
set<int> st;
for(int i = n; i >= 1; i--){
sort(q[i].begin(), q[i].end());
st.insert(i);
for(PII x : q[i]){
auto it = st.upper_bound(x.first);
if(it == st.begin()){
No();
}else{
ans[x.second] = *prev(it);
st.erase(prev(it));
}
}
}
cout << "Yes\n";
for(int i = 1; i <= n; i++) cout << ans[i] << " ";
return 0;
}
luogu - P3704 [SDOI2017] 数字表格
厉害的数学题(注意这题并不是斐波那契数列,因为 \(f_0\) = 0,这个导致我调了很久)
既然不是斐波那契数列,只能暴力推了,不妨设 \(n > m\),则求 \(\prod\limits_{d=1}^{n}{\prod\limits_{i=1}^{n}{\prod\limits_{j=1}^{m}{f_{\gcd(i,j)} [\gcd(i,j) == d] }}}\)
参考题解:https://www.luogu.com.cn/article/e5bx8otc
- \(\prod\limits_{d=1}^{n}{f[d]^{\sum\limits_{i=1}^{n/d}{\sum\limits_{j=1}^{m/d}{[\gcd(i,j) == 1]}}}}\)
- 考虑:\(\sum\limits_{i=1}^{n/d}{\sum\limits_{j=1}^{m/d}{[\gcd(i,j) == 1]}}\)
- 莫比乌斯反演:\(\sum\limits_{g=1}^{n}{\sum\limits_{i=1}^{n/d/g}{\sum\limits_{j=1}^{m/d/g}{\mu(g}}}\)
- \(\sum\limits_{g=1}^{n}{\mu(g) [\frac{n}{dg}][\frac{m}{dg}]}\)
- 换元法,设 \(T = dg\),则 \(\prod\limits_{T=1}^{n}{\prod\limits_{d|T}{{f_{d}}^{\mu(T/d)[n/T][m/T]}}}\)
- 最后提一提次数,就可以直接 整除分块+预处理 了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 1e6 + 3, V = 1e6;
const LL mod = 1e9 + 7;
LL qpow(LL A, LL B){
LL ret = 1;
while(B > 0){
if(B & 1) ret = ret * A % mod;
A = A * A % mod, B >>= 1;
}
return ret;
}
LL _pow(LL A, int B){
if(B == 0) return 1;
return (B < 0 ? qpow(A, mod - 2) : A);
}
LL f[MAXN], mu[MAXN], s[MAXN], is[MAXN];
bool vis[MAXN];
int main(){
ios::sync_with_stdio(0), cin.tie(0);
for(int i = 1; i <= V; i++) mu[i] = 1;
f[0] = 0, f[1] = 1;
for(int i = 2; i <= V; i++) f[i] = (f[i - 1] + f[i - 2]) % mod;
for(int i = 2; i <= V; i++){
if(vis[i]) continue;
for(int j = i; j <= V; j += i){
vis[j] = 1, mu[j] *= -1;
if(j % LL(i * i) == 0) mu[j] = 0;
}
}
s[0] = is[0] = 1;
for(int i = 1; i <= V; i++) s[i] = 1;
for(int i = 1; i <= V; i++){
for(int j = i; j <= V; j += i){
s[j] = (s[j] * _pow(f[i], mu[j / i])) % mod;
}
}
for(int i = 1; i <= V; i++){
s[i] *= s[i - 1], s[i] %= mod;
is[i] = qpow(s[i], mod - 2);
}
int T, n, m;
cin >> T;
while(T--){
cin >> n >> m;
if(n < m) swap(n, m);
LL ans = 1;
for(int l = 1, r; l <= m; l = r + 1){
r = min(n / (n / l), m / (m / l));
ans *= qpow(s[r] * is[l - 1] % mod, 1ll * (n / l) * (m / l) % (mod - 1));
ans %= mod;
}
cout << ans << "\n";
}
return 0;
}
MX - 捏捏
题面
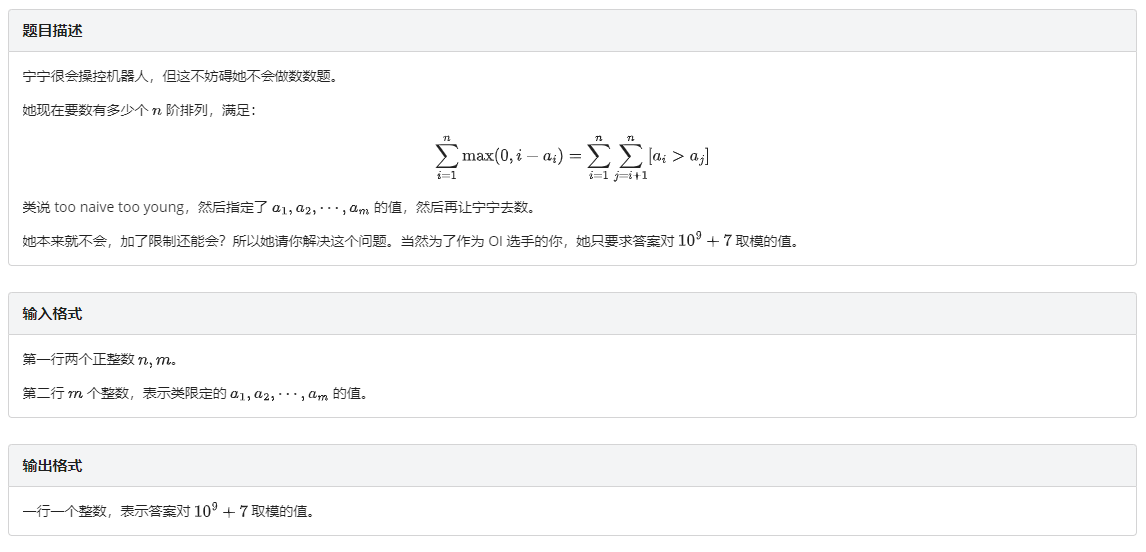
发现一个类似的题:P4769 [NOI2018] 冒泡排序 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
冒泡排序:冒泡排序 - OI Wiki (oi-wiki.org)
- 冒泡排序的交换次数 = 逆序对个数
- 注意到冒泡排序每次交换两个相邻的数,所以恰好减少一个逆序对数量,且排序最后没有逆序对,所以成立。
- \(\sum\limits_{i=1}^{n}{|i - a_i|} \cdot \frac{1}{2}\) 是冒泡排序交换次数的下界
- 对于全排列,每个点需要从 \(p_i\) 移动到 \(i\),设总距离为 \(\sum\limits_{i=1}^{n}{|i - a_i|}\),则冒泡排序每次会使得总距离减少 \(2\),下界就是这个东西了。
- 如果一个数排序过程既往右移,又往左移,则冒泡排序交换次数不能达到下界
- (显然
- 例如序列
3 2 1,第一次扫描得2 1 3,第二次扫描得1 2 3,发现2左右移动,所以不达到下界。
- 若存在 \(a_i > a_j > a_k\) 且 \(i < j < k\),则冒泡排序不能达到下界。
- (显然
复习一下 Dilworth 定理:
最长上升(下降)子序列长度 = 将序列划分为若干个不上升(不下降)子序列的最少序列个数。
问题转化为求多少个排列不存在长度为 \(3\) 的下降子序列,又根据 Dilworth 定理得:求多少个排列可以被最少分为 \(1\) 个或 \(2\) 个最长上升子序列。
考虑 dp,设 \(f_{i,j}\) 表示前 \(i\) 个数最大值 \(j\)。\(f_{i,j}\) 可以转移到 \(f_{i+1,k} (j < k)\) 和 \(f_{i+1,j}\),发现一个天然限制:\(i \le j\)。
在网格图上考虑,发现就是 \((0,0)\) 走到 \((n,n)\) 的方案数,不能超过对角线,模板卡特兰数。
如果考虑给出的前缀,设最大值 \(v\),则初始状态从 \((0,0)\) 变为了 \((m, v)\),则问题变为了 \((0,0)\) 走到 \((n-m, n-v)\),模板卡特兰数。
复习一下卡特兰数:
\((0,0)\) 走到 \((n,m)\) 不走对角线,方案数 \(C_{n+m}^{n} - C_{n+m}^{n-1}\)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e6 + 3, V = 1e6;
const LL mod = 1e9 + 7;
LL qpow(LL A, LL B){
LL ret = 1;
while(B > 0){
if(B & 1) ret = ret * A % mod;
A = A * A % mod, B >>= 1;
}
return ret;
}
LL fac[MAXN], ifac[MAXN];
LL C(int A, int B){
if(A < 0 || B < 0) return 0;
return fac[B] * ifac[A] % mod * ifac[B - A] % mod;
}
int a[MAXN];
int sum[MAXN];
int n, m;
void ADD(int x, int w){
for(; x <= n; x += (x & (-x))) sum[x] += w;
}
int QUE(int x){
int ret = 0;
for(; x >= 1; x -= (x & (-x))) ret += sum[x];
return ret;
}
bool check(){
LL ans = 0, sum = 0;
for(int i = 1; i <= m; i++){
ans += QUE(n - a[i] + 1);
ADD(n - a[i] + 1, 1);
sum += max(0, i - a[i]);
}
return sum != ans;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
freopen("nene.in", "r", stdin);
freopen("nene.out", "w", stdout);
fac[0] = 1;
for(int i = 1; i <= V; i++) fac[i] = fac[i - 1] * i % mod;
ifac[V] = qpow(fac[V], mod - 2);
for(int i = V - 1; i >= 0; i--) ifac[i] = ifac[i + 1] * (i + 1) % mod;
int v = 0;
cin >> n >> m;
for(int i = 1, x; i <= m; i++){
cin >> x, v = max(v, x), a[i] = x;
}
if(check()){
cout << 0;
return 0;
}
int h = n - m, w = n - v;
cout << (C(w, h + w) - C(w - 1, h + w) + mod) % mod;
return 0;
}
[WC2022] 杂题选讲 - 邓明扬 - stars
dp 状态设计好题,收藏了......
[ABC218H] Red and Blue Lamps
反悔贪心典题。
我们不妨设 \(R = \min(R, n - R)\)
题目可以两个相邻的 \(a_i\) 相加,问题转化为有 \(n\) 个数,最多选 \(R\) 个数,且要求选择的数不相邻(位置上不相邻)
反悔贪心和网络流建反边一样,为了反悔。具体的,当你选择一个 \(val\) 后,左右的元素需要被删除,但是为了反悔,你会给 \(val\) 重新赋值 \(val_i = val_l + val_r - i\),然后再次加入堆中。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 2e5 + 3;
int n, R, a[MAXN];
LL val[MAXN];
int vis[MAXN], nxt[MAXN], pre[MAXN];
void Erase(int x){
if(!x) return;
vis[x] = 1, nxt[pre[x]] = nxt[x], pre[nxt[x]] = pre[x];
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> R, R = min(R, n - R);
for(int i = 1; i < n; i++){
cin >> a[i];
}
LL ans = 0;
priority_queue<PII> pq;
for(int i = 1; i <= n; i++){
pre[i] = i - 1, nxt[i] = i + 1, val[i] = a[i] + a[i - 1]; // 题目可转化为:有 n 个位置,选择 R 个 val[i],要求选择的不能相邻
pq.push({val[i], i});
}
pre[1] = nxt[n] = 0;
while(R > 0){
while(!pq.empty() && vis[pq.top().second]) pq.pop();
if(pq.empty()) break;
int i = pq.top().second;
pq.pop();
R--, ans += val[i];
val[i] = val[pre[i]] + val[nxt[i]] - val[i];
pq.push({val[i], i}); // 给其反悔机会
vis[pre[i]] = vis[nxt[i]] = 1;
Erase(pre[i]), Erase(nxt[i]);
}
cout << ans;
return 0;
}
[AGC001F] Wide Swap
可以先转换为一个 \(q\) 数组,然后问题变为每次交换相邻两个之差大于等于 \(k\) 的,任然是要求字典序最小。
这似乎只是普通排序加上一个 \(k\) 的限制,能否直接归并排序做?
由于是归并排序,我们考虑证明两个区间合并后最优。
类似 \([i,i]\) 的长度为一的区间显然是最优的。
两个最优的区间合并,我们实现的思路大概是每次右侧的能向前移就移。
能够移动有两条限制:\(q_{i-1} > q_i\) 且 \(q_{i-1} - q_i \ge k\) 。合并即一个条件 \(q_{i-1} - q_i \ge k\)。
如果我们的做法不最优,则是存在一个右侧区间后面的东西先移动更优,或是左侧重排后更优,我们发现上面一行的式子都不会这样。
不过这只是我个人的感性理解。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 5e5 + 3;
int n, k;
int p[MAXN], q[MAXN], tmp[MAXN];
int mi[MAXN];
void Solve(int l, int r){
if(l == r) return;
int mid = (l + r) >> 1;
Solve(l, mid), Solve(mid + 1, r);
for(int i = l; i <= r; i++) tmp[i] = q[i];
mi[mid + 1] = 1e9;
for(int i = mid; i >= l; i--) mi[i] = min(mi[i + 1], tmp[i]);
for(int i = l, x = l, y = mid + 1; i <= r; i++){
if(x == mid + 1 || (y <= r && tmp[y] + k <= mi[x])){
q[i] = tmp[y], y++;
}else{
q[i] = tmp[x], x++;
}
}
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> k;
for(int i = 1; i <= n; i++){
cin >> p[i], q[p[i]] = i;
}
Solve(1, n);
for(int i = 1; i <= n; i++){
p[q[i]] = i;
}
for(int i = 1; i <= n; i++){
cout << p[i] << "\n";
}
return 0;
}
/*
*/
[ABC361G] Go Territory
如果考虑并查集,发现有 \(V ^2\) 个点,但是我们一开始就可以合并一些点,即将每一行一段区间直接当作一个点,点数大概是 \(V+n\) 个,然后双指针。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 2e5 + 5;
struct Edge{
int l, r, id;
}_e[MAXN * 5];
int n, k = 0, V = 2e5 + 2;
vector<int> p[MAXN];
vector<Edge> e[MAXN];
int fa[MAXN * 5];
int Getf(int x){ return fa[x] == x ? x : fa[x] = Getf(fa[x]); }
void Merge(int x, int y){
x = Getf(x), y = Getf(y), fa[x] = y;
}
bool check(Edge i, Edge j){
return max(i.l, j.l) <= min(i.r, j.r);
}
int main(){
cin >> n;
for(int i = 1, x, y; i <= n; i++){
cin >> x >> y, p[x].push_back(y);
}
k = 1, fa[1] = 1;
for(int i = 0; i <= V; i++){
p[i].push_back(-1), p[i].push_back(V + 1);
sort(p[i].begin(), p[i].end());
for(int j = 1; j < p[i].size(); j++){
int l = p[i][j - 1] + 1, r = p[i][j] - 1;
if(l > r) continue;
k++, fa[k] = k, _e[k] = {l, r, i}, e[i].push_back({l, r, k});
}
if(i == 0){
for(Edge E : e[i]){
Merge(1, E.id);
}
continue;
}
if(e[i][0].l == 0) Merge(1, e[i][0].id);
for(int j = 0, h = 0; j < e[i].size(); j++){
h = max(0, h - 1);
while(h < e[i - 1].size() && !check(e[i][j], e[i - 1][h]) && e[i - 1][h].r < e[i][j].l){
h++;
}
while(h < e[i - 1].size() && check(e[i][j], e[i - 1][h])){
Merge(e[i][j].id, e[i - 1][h].id);
h++;
}
}
}
LL ans = 0;
for(int i = 2; i <= k; i++){
if(Getf(1) != Getf(i)){
ans += _e[i].r - _e[i].l + 1;
}
}
cout << ans;
return 0;
}
/*
20
5 0
2 1
3 1
4 3
0 4
2 4
1 4
5 2
0 3
1 3
0 5
1 2
1 1
1 0
4 0
2 0
3 5
5 4
4 4
3 3
1
*/
luogu - P11036 【MX-X3-T3】「RiOI-4」GCD 与 LCM 问题
好玩题,就好玩一下吧!
发现对于 \(a\) 为奇数,可以答案 \(a, 1, 2, a-2\)。
设 \(e\) 为 \(a\) 的 lowbit,推测答案为 \(a, 1, 2e, a - 2e\),考虑证明。我们需要证明 \(lcm(2e, a - 2e) = 2a + 4e\)。
\(lcm\) 两边都有 \(e\),得 \(e lcm(2, \frac{a}{e} - 2) = 2a + 4e\)。由于 \(\frac{a}{e}\) 为奇数,减二后还是奇数,所以 \(lcm\) 两边互质!!!
得 \(2e( \frac{a}{e} - 2) = 2a + 4e\),成立!!!
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
LL lowbit(LL x){ return x & (-x); }
int main(){
ios::sync_with_stdio(0), cin.tie(0);
int T, a;
cin >> T;
while(T--){
cin >> a;
int lo = lowbit(a);
cout << 1 << " " << 2 * lo << " " << a + 2 * lo << "\n";
}
return 0;
}
luogu - P7205 [COCI2019-2020#3] Drvca
法一:暴力搜索 + 剪枝(不会复杂度证明,所以略)
法二:
根据鸽巢原理可以的到至少有一个序列的前两项为 \((1,2)\) 或 \((2,3)\) 或 \((1,3)\),然后 \(O(n^2)\) 检查。具体的:枚举下一项,然后判断剩余的数能否组成等差数列。
至于判断剩余的数可以使用链表和 map 优化
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e5 + 3;
int n, a[MAXN];
int pre[MAXN], nxt[MAXN];
multiset<int> st;
inline void Erase(int x){
if(pre[x]){
st.erase(st.find(a[x] - a[pre[x]]));
}
if(nxt[x]){
st.erase(st.find(a[nxt[x]] - a[x]));
}
if(pre[x] && nxt[x]) st.insert(a[nxt[x]] - a[pre[x]]);
nxt[pre[x]] = nxt[x], pre[nxt[x]] = pre[x];
}
bool check(){ return st.size() > 0 && st.size() != n && *st.begin() == *st.rbegin(); }
void finish(){
vector<int> vt, _vt;
vector<bool> vis(n + 3);
for(int i = nxt[0]; i > 0; i = nxt[i]) vt.push_back(a[i]), vis[i] = 1;
for(int i = 1; i <= n; i++){
if(!vis[i]) _vt.push_back(a[i]);
}
cout << vt.size() << "\n";
for(int x : vt) cout << x << " ";
cout << "\n" << _vt.size() << "\n";
for(int x : _vt) cout << x << " ";
exit(0);
}
void doit(int x, int y, int z){
st.clear();
for(int i = 1; i <= n; i++){
if(i > 1) st.insert(a[i] - a[i - 1]);
pre[i] = i - 1, nxt[i] = i + 1;
}
nxt[0] = 1, nxt[n] = 0, Erase(x), Erase(y);
if(z > 0){
Erase(z);
if(a[z] - a[y] != a[y] - a[x]) return;
}
int d = a[y] - a[x];
if(check()) finish();
for(int i = 4, la = max(z, y); i <= n; i++){
if(a[i] - a[la] == d){
Erase(i), la = i;
}
if(check()) finish();
}
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for(int i = 1; i <= n; i++){
cin >> a[i];
}
sort(a + 1, a + 1 + n);
if(n == 2){
cout << 1 << "\n" << a[1] << "\n" << 1 << "\n" << a[2];
return 0;
}
doit(1, 2, 0), doit(1, 3, 0), doit(2, 3, 0), doit(1, 2, 3);
cout << -1;
return 0;
}
luogu - P11037 【MX-X3-T4】「RiOI-4」上课
方差是可以推式子的,暴力推,推式子不用拆开平均数,则最后得到 \(\frac{\sum{a_i^2}}{n} - \mu^2\)。
回到题目中,发现题目中的询问平均数是确定的,则问题转化为求 \(\sum{a_i^2}\) 的最小值。
考虑一个数加一后的平方变化 \((x+1)^2 = x^2 + 2x + 1\),所以每次对于最小的 \(a_i\) 加就可以了,发现值域 \(1e6\),统一加则复杂度 \(O(V)\)。(离线处理)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e6 + 3, V = 1e6;
const LL mod = 998244353;
LL qpow(LL A, LL B){
LL ret = 1;
while(B > 0){
if(B & 1) ret = ret * A % mod;
A = A * A % mod, B >>= 1;
}
return ret;
}
struct Ask{
LL x;
int id;
}q[MAXN];
int n, Q, cnt[MAXN];
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> Q;
LL sum = 0, ans = 0;
for(int i = 1, l, r; i <= n; i++){
cin >> l >> r, sum += l, ans += 1ll * l * l % mod, ans %= mod;
cnt[l + 1]++, cnt[r + 1]--;
}
for(int i = 1; i <= V + 1; i++){
cnt[i] += cnt[i - 1];
}
for(int i = 1; i <= Q; i++){
cin >> q[i].x, q[i].id = i;
}
sort(q + 1, q + 1 + Q, [](Ask i, Ask j){ return i.x < j.x; });
LL in = qpow(n, mod - 2);
for(int i = 1, j = 0; i <= Q; i++){
while(sum < q[i].x){
if(sum + cnt[j] > q[i].x){
int s = q[i].x - sum;
sum += s, cnt[j] -= s, ans += 1ll * s * (2 * (j - 1) + 1) % mod, ans %= mod;
break;
}
sum += cnt[j], ans += 1ll * cnt[j] * (2 * (j - 1) + 1) % mod, ans %= mod;
j++;
}
q[i].x %= mod;
q[i].x = (ans * in % mod - in * in % mod * q[i].x % mod * q[i].x % mod + mod) % mod;
}
sort(q + 1, q + 1 + Q, [](Ask i, Ask j){ return i.id < j.id; });
for(int i = 1; i <= Q; i++){
cout << q[i].x << "\n";
}
return 0;
}
luogu - P7114 [NOIP2020] 字符串匹配
参考题解:https://www.luogu.com.cn/article/n4eaq3p6
关于 fail 数组有一个结论:字符串 \(S\) 的最短周期长度为 \(|S| - fail[S]\)。具体证明见 oi-wiki,是就是这题:https://www.cnblogs.com/huangqixuan/p/18446558#luogu---p4391-boi2009-radio-transmission-无线传输
枚举 \(i\),然后枚举 \(AB\) 长度,预处理优化统计答案,复杂度调和级数 和 字符集大小,\(O(n \log n + 26n)\)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 2e6 + 3;
int n;
string s;
int nex[MAXN];
int _sum[MAXN], sum[MAXN][27], tmp[27];
void work(){
cin >> s, n = s.size(), s = " " + s;
nex[1] = 0;
for(int i = 2, j = 0; i <= n; i++){
while(j > 0 && s[j + 1] != s[i]) j = nex[j];
j += s[j + 1] == s[i];
nex[i] = j;
}
for(int i = 1; i <= n; i++){
for(int j = 0; j <= 26; j++) sum[i][j] = 0;
}
for(int j = 0; j < 26; j++) tmp[j] = 0;
for(int i = 1, cnt = 0; i <= n; i++){
int col = s[i] - 'a';
cnt += (tmp[col] % 2 == 1 ? -1 : 1), tmp[col]++;
sum[i][cnt]++;
}
for(int i = 1; i <= n; i++) for(int j = 0; j <= 26; j++) sum[i][j] = sum[i][j] + sum[i - 1][j];
for(int i = 1; i <= n; i++) for(int j = 1; j <= 26; j++) sum[i][j] = sum[i][j - 1] + sum[i][j];
for(int j = 0; j < 26; j++) tmp[j] = 0;
for(int i = n, cnt = 0; i >= 1; i--){
int col = s[i] - 'a';
cnt += (tmp[col] % 2 == 1 ? -1 : 1), tmp[col]++;
_sum[i] = cnt;
}
LL ans = 0;
for(int i = 1; i <= n; i++){
for(int l = 1; l <= n; l++){
if(l * i >= n) break;
int r = i * l - nex[i * l];
if(i == 1 || l % r == 0){
ans += sum[l - 1][_sum[i * l + 1]];
}
}
}
cout << ans << "\n";
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
int T; cin >> T; while(T--) work();
return 0;
}
luogu - P11021 「LAOI-6」区间测速
两个绝对值有些复杂,考虑排序 \(t\) 消掉一个,然后考虑,对于固定右端点 \(r\),发现只用考虑左端点 \(r-1\),为什么?
要求的相当于是一个平均值,即平均速度,如果 \(l\) 再向扩大,则平均值一定再最小值和最大值之间。
于是考虑维护,可以用 set,也可以直接排序+二分。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 100010;
struct Node{
int x, t;
}a[MAXN], _a[MAXN];
int n, m, v[MAXN], _v[MAXN];
int Find(int w){
int l = 0, r = n;
while(l < r){
int mid = (l + r + 1) >> 1;
if(_a[mid].t <= w) l = mid;
else r = mid - 1;
}
return l;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; i++){
cin >> a[i].x >> a[i].t, _a[i] = a[i];
}
sort(_a + 1, _a + n + 1, [](Node i, Node j){ return i.t < j.t; });
for (int i = 1; i < n; i++){
v[i] = _v[i] = abs(_a[i + 1].x - _a[i].x) / abs(_a[i + 1].t - _a[i].t);
}
sort(_v + 1, _v + n);
for(int q = 1, u, t; q <= m; q++){
cin >> u >> t;
int l, r, pos = Find(a[u].t), k = n - 1;
if(max(v[pos - 1], v[pos]) == _v[k]){
k--;
}
if(min(v[pos - 1], v[pos]) == _v[k]){
k--;
}
if(_a[pos - 1].t < t && _a[pos + 1].t > t) l = pos - 1, r = pos + 1;
else l = Find(t), r = l + 1;
int v1 = (pos > 0 ? abs(a[u].x - _a[l].x) / abs(t - _a[l].t) : 0);
int v2 = (pos < n ? abs(a[u].x - _a[r].x) / abs(_a[r].t - t) : 0);
cout << max({v1, v2, _v[k]}) << "\n";
}
return 0;
}
luogu - P10592 BZOJ4361 isn
MX 出原题,但是场上不会。
考虑利用容斥求出保留 \(l\) 个数的方案数:保留一个,剩余的不看顺序。设 \(dp_{i,j}\) 表示以 \(i\) 结尾长度为 \(j\) 的不降子序列个数,树状数组求解复杂度 \(O(n^2 \log n)\)。
则保留 \(i\) 个的方案数位 \(\sum{dp_{k,l-1}}(n-l+1) - \sum{dp_{k,l}})(l)\),然后再乘以 \((n-l)!\)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const LL mod = 1e9 + 7;
const int MAXN = 2000 + 3;
int n, a[MAXN];
LL dp[MAXN][MAXN], sum[MAXN][MAXN], fac[MAXN];
void init(){
vector<int> vt;
map<int, int> mp;
for(int i = 1; i <= n; i++) cin >> a[i], vt.push_back(a[i]);
sort(vt.begin(), vt.end());
for(int i = 0, cnt = 0; i < vt.size(); i++){
if(i == 0 || vt[i] != vt[i - 1]) mp[vt[i]] = ++cnt;
}
for(int i = 1; i <= n; i++) a[i] = mp[a[i]];
}
void ADD(int x, int y, LL w){
for(; y <= n; y += (y & (-y))) sum[x][y] = (sum[x][y] + w) % mod;
}
LL QUE(int x, int y){
LL ret = 0;
for(; y > 0; y -= (y & (-y))) ret = (ret + sum[x][y]) % mod;
return ret;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
//freopen("delete.in", "r", stdin);
//freopen("delete.out", "w", stdout);
cin >> n;
init();
fac[0] = 1;
for(int i = 1; i <= n; i++) fac[i] = fac[i - 1] * i % mod;
ADD(0, 1, 1);
dp[1][0] = 1;
for(int i = 1; i <= n; i++){
for(int j = i; j >= 1; j--){
dp[i][j] = QUE(j - 1, a[i]), ADD(j, a[i], dp[i][j]);
}
}
LL ans = 0;
for(int l = 1; l < n; l++){
LL sss = 0;
for(int i = 1; i <= n; i++){
sss = (sss + dp[i][l - 1] * (n - l + 1) % mod) % mod;
sss = (sss - dp[i][l] * l % mod + mod) % mod;
}
ans = (ans + sss * fac[n - l] % mod) % mod;
}
cout << ans;
return 0;
}
luogu - P11017 Hide And Seek
全图太复杂了,考虑找到一个子图,满足追捕者抓不到逃跑者。
当然是要尝试找到最小子图。我们发现一菊花子图一定可以追到逃跑者,又发现一个最小子图如下(该子图追捕者抓不到逃跑者),前提是逃跑者到达根(橙色点):
我们考虑找到这个最小子图的根(橙色点),然后判断两人到这点的距离,要求逃跑者到的时候,追捕者距离至少一步(显然若少于一步就直接抓到了)。可以 dfs 实现。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<LL, int>;
const int MAXN = 2e5 + 3;
int n, a[MAXN];
vector<int> eg[MAXN];
int len[2][MAXN];
void dfs(int x, int op, int l){
len[op][x] = l;
for(int nxt : eg[x]){
if(len[op][nxt] == -1){
dfs(nxt, op, l + 1);
}
}
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
int T;
cin >> T;
while(T--){
int p, q;
cin >> n >> p >> q;
for(int i = 1; i <= n; i++) eg[i].clear(), a[i] = 0;
for(int i = 1, U, V; i < n; i++){
cin >> U >> V, eg[U].push_back(V), eg[V].push_back(U);
}
for(int i = 1; i <= n; i++){
if(eg[i].size() < 3) continue;
int cnt = 0;
for(int j : eg[i]){
if(eg[j].size() > 1) cnt++;
}
a[i] = cnt >= 3; // 可以作为最小子图的根
}
for(int i = 1; i <= n; i++) len[0][i] = len[1][i] = -1;
dfs(q, 0, 0), dfs(p, 1, 0);
int ans = 0;
for(int i = 1; i <= n; i++){
if(a[i] && len[1][i] - len[0][i] >= 2){
ans = 1;
break;
}
}
cout << (ans ? "Drifty\n" : "hgcnxn\n");
}
return 0;
}
CF416E - President's Path
首先 \(O(n^3)\) 跑一遍 Floyd,然后枚举 \(s,t\),再枚举每条边 \(O(1)\) 检查,不过边数是 \(O(n^2)\) 的,复杂度 \(O(n^4)\),怎么办?
考虑枚举中转点,中转点需要满足 \(l(s,p) + l(p,t) = l(s,t)\),每个 \(p\) 的贡献是 \(s\) 到 \(p\) 最短路上每条连接 \(p\) 的边数。复杂度 \(O(n^3)\)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<LL, int>;
const int MAXN = 500 + 3;
int n, m;
LL dp[MAXN][MAXN], cnt[MAXN], ans[MAXN][MAXN];
int e[MAXN][MAXN];
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++) dp[i][j] = 1e18, e[i][j] = 1e9 + 7;
dp[i][i] = 0;
}
for(int i = 1, U, V, W; i <= m; i++){
cin >> U >> V >> W;
e[U][V] = min(e[U][V], W), e[V][U] = min(e[V][U], W);
dp[U][V] = min(dp[U][V], 1ll * W), dp[V][U] = min(dp[V][U], 1ll * W);
}
for(int h = 1; h <= n; h++){
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++) dp[i][j] = min(dp[i][j], dp[i][h] + dp[h][j]);
}
}
for(int s = 1; s <= n; s++){
for(int p = 1; p <= n; p++) cnt[p] = 0;
for(int t = 1; t <= n; t++){
for(int p = 1; p <= n; p++){
if(e[p][t] <= 1e9 && dp[s][p] + e[p][t] == dp[s][t]) cnt[t]++;
}
}
for(int t = 1; t <= n; t++){
for(int p = 1; p <= n; p++){
if(dp[s][p] + dp[p][t] == dp[s][t]) ans[s][t] += cnt[p];
}
}
}
for(int s = 1; s <= n; s++){
for(int t = s + 1; t <= n; t++) cout << ans[s][t] << " ";
}
return 0;
}
luogu - P11013 「ALFR Round 4」C 粉碎
发现:如果 \(a_i\) 可以被删除,则 \(a_j(1 \le j \le i)\) 都可以被删除。
设 \(dp_{i,0/1}\) 表示 \(a_i\) 能否被删除、保留,然后就是转移了(注意题目要求了能删就立即删)。
只不过 dp 转移的时候根据我们的发现,需要用一个 ans 记录现在可以删到那里了(可以视作动态修改,只是一个标记就实现完了)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 5e5 + 3;
int n, dp[MAXN][2], a[MAXN], pre[MAXN], mp[MAXN];
int ans = 0;
int ret(int i, int j){ return dp[i][j] | (j == 1 ? i <= ans : 0); }
int main(){
ios::sync_with_stdio(0), cin.tie(0);
int T;
cin >> T;
while(T--){
cin >> n;
for(int i = 1; i <= n; i++) mp[i] = 0;
for(int i = 1; i <= n; i++){
cin >> a[i], pre[i] = mp[a[i]], mp[a[i]] = i;
}
ans = 0;
for(int i = 0; i <= n; i++) dp[i][0] = dp[i][1] = 0;
dp[0][1] = 1;
for(int i = 1; i <= n; i++){
dp[i][1] |= ret(pre[i], 0), dp[i][0] |= ret(pre[i], 1);
if(dp[i][1]) ans = i;
}
cout << ans << "\n";
}
return 0;
}
luogu - P11018 Monochrome Tree
很好的树形 dp 题。
这题不能以树上背包的视角看,即不能将树拆成二叉树(Hack 就是第二个样例),因为有子树反转操作,所以思路是先合并儿子,然后分别转移链操作、子树操作。
大力分类讨论!!!有一些多余转移可以省去,但是需要小心。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 2e5 + 3;
int n, col[MAXN];
vector<int> eg[MAXN];
int dp[MAXN][2][2], _dp[MAXN][2][2];
void dfs(int x, int dad){
if(eg[x].size() - (dad > 0) == 0){
if(col[x] == 1){
dp[x][1][0] = 0, dp[x][1][1] = 2;
dp[x][0][1] = 1, dp[x][0][0] = 1;
}else{
dp[x][0][0] = 0, dp[x][0][1] = 2;
dp[x][1][1] = 1, dp[x][1][0] = 1;
}
return;
}
for(int i = 0; i < 2; i++){
for(int j = 0; j < 2; j++) _dp[x][i][j] = 1e9;
}
int ooo = 0;
for(int nxt : eg[x]){
if(nxt == dad) continue;
dfs(nxt, x), ooo++;
if(ooo == 1){
for(int i = 0; i < 2; i++){
for(int j = 0; j < 2; j++) _dp[x][i][j] = dp[nxt][i][j];
}
continue;
}
// 这里 dp 做临时数组
for(int i = 0; i < 2; i++){
for(int j = 0; j < 2; j++) dp[x][i][j] = _dp[x][i][j], _dp[x][i][j] = 1e9;
}
for(int i = 0; i < 2; i++){
for(int j = 0; j < 2; j++){
for(int k = 0; k < 2; k++){
_dp[x][i][j ^ k] = min(_dp[x][i][j ^ k], dp[x][i][j] + dp[nxt][i][k]);
}
}
}
}
for(int i = 0; i < 2; i++){
for(int j = 0; j < 2; j++) dp[x][i][j] = 1e9;
}
int c = col[x];
dp[x][c][0] = min(_dp[x][c][0], _dp[x][c][1] + 1); // 链操作
dp[x][c^1][1] = min(_dp[x][c^1][1], _dp[x][c^1][0] + 1);
dp[x][c^1][0] = min(dp[x][c^1][0], dp[x][c][0] + 1); // 子树操作
dp[x][c][1] = min(dp[x][c][1], dp[x][c^1][1] + 1);
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for(int i = 1; i <= n; i++){
cin >> col[i];
}
for(int i = 1, U, V; i < n; i++){
cin >> U >> V, eg[U].push_back(V), eg[V].push_back(U);
}
dfs(1, 0);
cout << min(dp[1][1][0], dp[1][1][1]);
return 0;
}
[ABC314Ex] Disk and Segments
模拟退火水题(https://www.cnblogs.com/huangqixuan/articles/18415944 )。和 P1337 几乎一模一样,但是需要卡精度,同时也需要知道如何求点到直线的距离。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
using i128 = __int128_t;
namespace CG{
struct Node{
double x, y;
Node operator- (Node j){ return {x - j.x, y - j.y}; }
};
double ABS(double x){ return max(x, -x); } // 实数绝对值
int cmp(double x){ return (ABS(x) < 1e-10 ? 0 : (x < 0 ? -1 : 1)); } // 优化精度误差
double len(Node x, Node y){ return (x.x - y.x) * (x.x - y.x) + (x.y - y.y) * (x.y - y.y); } // 欧几里得距离的平方
double dot(Node x, Node y){ return x.x * y.x + x.y * y.y; } // 点乘
double cross(Node x, Node y){ return x.x * y.y - x.y * y.x; } // 叉乘
double postoeg(Node p, Node a, Node b){ // 点到直线距离
if(dot(b - a, p - a) < 0) return sqrt(len(p, a));
if(dot(a - b, p - b) < 0) return sqrt(len(p, b));
return ABS(cross(p - a, b - a)) / sqrt(len(b, a));
}
}
const int MAXN = 1000 + 3;
int n;
CG::Node a[MAXN][2];
double dis, ansx, ansy;
mt19937 rnd(time(0));
double Rnd(){ return rand() / double(RAND_MAX); }
double ADD(double x, double y){
double ret = 0;
for(int i = 1; i <= n; i++){
ret = max(ret, CG::postoeg({x, y}, a[i][0], a[i][1]));
}
if(ret < dis) ansx = x, ansy = y, dis = ret;
return ret;
}
void doit(){
double t = 100000, down = 0.9999, nowx = ansx, nowy = ansy;
while(t > 0.000001){
double nxtx = nowx + (Rnd() * 2 - 1) * t;
double nxty = nowy + (Rnd() * 2 - 1) * t;
double change = ADD(nxtx, nxty) - ADD(nowx, nowy);
if(exp(- change / t) > Rnd()){ // 多项式接受
nowx = nxtx, nowy = nxty;
}
t = t * down;
}
for(int d = 1; d <= 100000; d++){
double nxtx = ansx + (Rnd() * 2 - 1) * t;
double nxty = ansy + (Rnd() * 2 - 1) * t;
ADD(nxtx, nxty);
}
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n, ansx = 0, ansy = 0;
for(int i = 1; i <= n; i++){
cin >> a[i][0].x >> a[i][0].y >> a[i][1].x >> a[i][1].y;
ansx += (a[i][0].x + a[i][1].x) / 2.0, ansy += (a[i][0].y + a[i][1].y) / 2.0;
}
ansx /= n, ansy /= n, dis = ADD(ansx, ansy); // 随意选择一个开始位置
doit(), doit(), doit();
cout << fixed << setprecision(8) << dis;
return 0;
}
MX - 空
题面
(题意转化没有必要)
一个无向图,求任意一个四元环。
无向边 \((i,j)\),如果 \(deg_i < deg_j\) 就连有向边 \((i,j)\)(设 \(n\) 为图中点数,\(m\) 为无向图中边数,\(deg_i\) 表示无向图度数,,\(d_i\) 表示有向图出度):
- 若 \(deg_i \le \sqrt{m}\),得 \(d_i \le \sqrt{m}\)
- 否则,任意有向边 \((i,j)\) 的 \(j\) 都有 \(deg_j > \sqrt{m}\),得 \(d_i \le \sqrt{m}\)。
这样的有向图的出度都是 \(\sqrt{m}\) 的,且是没有环的有向图。可以分类讨论求四元环(分类讨论每条边的定向,不过本质不同的有向四元环只有 3 个)。
luogu - P1989 无向图三元环计数
和 MX - 空 主要思想是类似的。
这题是求三元环,但是需要具体统计个数。
统计三元环个数可以从排序的角度来看,我们按照 \((deg_i,i)\) 这样的二元组排序,然后连边。
然后可以直接类似代码那种统计。非常方便。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 2e5 + 3;
int n, m, deg[MAXN], vis[MAXN];
PII EG[MAXN];
vector<int> eg[MAXN];
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
for(int i = 1, U, V; i <= m; i++){
cin >> U >> V, deg[U]++, deg[V]++, EG[i] = {U, V};
}
for(int i = 1; i <= m; i++){
int U = EG[i].first, V = EG[i].second;
if(deg[U] > deg[V] || (deg[U] == deg[V] && U > V)) swap(U, V);
eg[U].push_back(V);
}
LL ans = 0;
for(int u = 1; u <= n; u++){
for(int w : eg[u]) vis[w] = u;
for(int v : eg[u]){
for(int w : eg[v]){
if(vis[w] == u) ans++;
}
}
}
cout << ans;
return 0;
}
CF1746F - Kazaee
考虑随机化。\(x\) 随机映射到 \(y\) 上,然后求 \(\sum\),判断是否被 \(k\) 整除,这样做正确率是多少?
- \(k=1\) 可以忽略
- 考虑 \(k\ge 2\),错误率不会大于 \(\frac{1}{2}\),然后就可以做了(多个树状数组维护)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 3e5 + 3, T = 30;
map<int, int> mp;
mt19937 rnd(time(0));
int tot, W[MAXN * 2][T];
int Make(LL w){
if(mp.find(w) != mp.end()) return mp[w];
tot++, mp[w] = tot;
for(int t = 0; t < T; t++) W[tot][t] = rnd() % LL(2e9) + 1;
return tot;
}
LL sum[T][MAXN], a[MAXN];
int n, Q;
void ADD(int x, int op){
int id = Make(a[x]);
for(int t = 0; t < T; t++){
int w = W[id][t];
for(int y = x; y <= n; y += (y & (-y))) sum[t][y] += w * op;
}
}
LL QUE(int t, int x){
LL ret = 0;
for(; x > 0; x -= (x & (-x))) ret += sum[t][x];
return ret;
}
bool check(int l, int r, int k){
for(int t = 0; t < T; t++){
LL S = QUE(t, r) - QUE(t, l - 1);
if(S % k > 0) return 0;
}
return 1;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> Q;
for(int i = 1; i <= n; i++){
cin >> a[i];
int nx = i + (i & (-i)), id = Make(a[i]);
for(int t = 0; t < T; t++){
int w = W[id][t];
sum[t][i] += w;
if(nx <= n) sum[t][nx] += sum[t][i];
}
}
for(int q = 1, op, l, r, k; q <= Q; q++){
cin >> op;
if(op == 1){
cin >> l >> r;
ADD(l, -1), a[l] = r, ADD(l, 1);
}else{
cin >> l >> r >> k;
cout << (k == 1 || check(l, r, k) ? "YES" : "NO") << "\n";
}
}
return 0;
}
luogu - P3953 [NOIP2017 提高组] 逛公园
看似图论,实则 dp。
注意到 \(k \le 50\),试着将 \(k\) 也背进状态,\(dp_{i,j}\) 表示 \(1\) 到 \(j\) 满足 \(dis = mindis(i,j) + k\) 的路径数,转移可以解个方程。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 2e5 + 3;
int n, m, K, mod;
int dp[MAXN], op = 0;
vector<PII> eg[MAXN], _eg[MAXN];
int mp[MAXN][53];
bool vis[MAXN][53];
int dfs(int x, int k){
if(k < 0) return 0;
// d[nx] + _k + w= d[x] + k
// _k = d[x] + k - w - d[nx]
if(vis[x][k]){
op = 1;
return 0;
}
if(mp[x][k] >= 0) return mp[x][k];
vis[x][k] = 1, mp[x][k] = 0;
for(PII e : _eg[x]){
int nx = e.first, w = e.second;
mp[x][k] = (mp[x][k] + dfs(nx, dp[x] + k - w - dp[nx])) % mod;
}
vis[x][k] = 0;
return mp[x][k];
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
int T;
cin >> T;
while(T--){
op = 0;
cin >> n >> m >> K >> mod;
for(int i = 1; i <= n; i++) eg[i].clear(), _eg[i].clear();
for(int i = 1, U, V, W; i <= m; i++){
cin >> U >> V >> W;
eg[U].push_back({V, W}), _eg[V].push_back({U, W});
}
priority_queue<PII> pq;
for(int i = 1; i <= n; i++) dp[i] = 1e9;
pq.push({0, 1}), dp[1] = 0;
while(!pq.empty()){
PII w = pq.top();
int x = w.second;
pq.pop();
if(dp[x] < -w.first) continue;
for(PII e : eg[x]){
int nx = e.first, nw = dp[x] + e.second;
if(dp[nx] > nw){
dp[nx] = nw, pq.push({-nw, nx});
}
}
}
for(int i = 1; i <= n; i++){
for(int j = 0; j <= K; j++) mp[i][j] = -1;
}
if(dp[n] >= 1e9){
cout << 0 << "\n";
continue;
}
dfs(1, 0); // 判负环
mp[1][0] = 1;
LL ans = 0;
for(int k = 0; k <= K; k++) ans += dfs(n, k), ans %= mod;
cout << (op ? -1 : ans) << "\n";
}
return 0;
}
luogu - P2474 [SCOI2008] 天平
差分约束题。
如果枚举 \(i,j\),考虑如何 check。\(A+B > i+j\) 可以变换为 \(A-i > B-j\) 或 \(A-j>B-i\)。
我们求出任意 \(w_i-w_j\) 的最大值和最小值。具体可以初始得到一些限制,然后差分约束解出来。差分约束也可以使用 Floyd,比 Spfa 好写很多。
然后就是非类讨论,判断解集。有些细节。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int n, A, B;
int mx[53][53], mi[53][53]; // w_i - w_j 的最值
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> A >> B;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
char ch; cin >> ch;
if(i == j || ch == '=') mx[i][j] = mi[i][j] = 0;
else if(ch == '?') mx[i][j] = 2, mi[i][j] = -2;
else if(ch == '-') mx[i][j] = -1, mi[i][j] = -2;
else if(ch == '+') mx[i][j] = 2, mi[i][j] = 1;
}
}
for(int h = 1; h <= n; h++){
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){ // Floyd 替换 Spfa
mx[i][j] = min(mx[i][j], mx[i][h] + mx[h][j]);
mi[i][j] = max(mi[i][j], mi[i][h] + mi[h][j]);
}
}
}
int ans1 = 0, ans2 = 0, ans3 = 0;
for(int i = 1; i <= n; i++){
for(int j = i + 1; j <= n; j++){
if(i == A || j == B || i == B || j == A) continue;
// A + B > i + j
// A - j > i - B || A - i > B - j (注意这里是 或)
if(mi[A][j] > mx[i][B] || mi[A][i] > mx[j][B]) ans1++;
if((mi[A][j] == mx[i][B] && mx[A][j] == mi[i][B]) || (mi[A][i] == mx[j][B] && mx[A][i] == mi[j][B])) ans2++;
if(mx[A][j] < mi[i][B] || mx[A][i] < mi[j][B]) ans3++;
}
}
cout << ans1 << " " << ans2 << " " << ans3;
return 0;
}
luogu - P10894 虚树
树形 dp。
容易得到转移式子:\(f_i = \prod\limits_{s\in son_i}{(f_s + 1)} + \sum\limits_{s\in son_i}{f_s}\)。接着就有了 \(O(nm)\) 的做法,考虑预处理优化。
\(f_x\) 对父亲的贡献:\(f_x \times (\prod\limits_{y\in bro_i}{(f_y + 1)} + 1)\)。那么 \(f_x\) 对根的贡献就是一个前缀积。预处理即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 5e5 + 3;
const LL mod = 998244353;
LL qpow(LL A, LL B){
LL ret = 1;
while(B > 0){
if(B & 1) ret = ret * A % mod;
A = A * A % mod, B >>= 1;
}
return ret;
}
int n, m;
vector<int> eg[MAXN];
LL f[MAXN], g[MAXN];
void dfs(int x, int dad){
vector<int> son;
for(int nxt : eg[x]){
if(nxt == dad) continue;
dfs(nxt, x), son.push_back(nxt);
}
LL sum = 1;
for(int nxt : son) sum = sum * (f[nxt] + 1) % mod;
for(int nxt : son){
LL _sum = sum * qpow((f[nxt] + 1) % mod, mod - 2);
g[nxt] = (_sum + 1) % mod;
}
f[x] = sum;
for(int nxt : son) f[x] = (f[x] + f[nxt]) % mod;
}
void _dfs(int x, int dad){
for(int nxt : eg[x]){
if(nxt == dad) continue;
g[nxt] = g[nxt] * g[x] % mod;
_dfs(nxt, x);
}
g[x] = g[x] * f[x] % mod;
g[x] = (f[1] - g[x] + mod) % mod;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for(int i = 1, U, V; i < n; i++){
cin >> U >> V;
eg[U].push_back(V), eg[V].push_back(U);
}
dfs(1, 0);
g[1] = 1;
_dfs(1, 0);
cin >> m;
for(int q = 1, x; q <= m; q++){
cin >> x;
cout << g[x] << "\n";
}
return 0;
}
luogu - P4926 [1007] 倍杀测量者
将乘法差分系统通过求 log2() 转化为普通的加法差分系统。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using Edge = pair<int, double>;
const int MAXN = 1000 + 3;
const double eps = 1e-8;
struct Input{
int o, A, B, k;
}E[MAXN * 2];
double l[MAXN];
int vis[MAXN], cnt[MAXN];
int n, m1, m2, ooo;
vector<Edge> eg[MAXN];
queue<int> que;
void Record(int x, double w){
if(ooo) return;
if(l[x] > w){
l[x] = w;
if(!vis[x]){
vis[x] = 1, cnt[x]++, que.push(x);
if(cnt[x] >= n + 1){
ooo = 1;
}
}
}
}
bool check(double T){
for(int i = 0; i <= n; i++) eg[i].clear();
for(int i = 1; i <= m1; i++){
if(E[i].o == 1){
if(E[i].k <= T) return 0;
double k = log2(E[i].k - T);
// A >= k + B
// B <= A - k
eg[E[i].A].push_back({E[i].B, - k});
}else{
double k = log2(E[i].k + T);
// A + k - ... >= B
eg[E[i].A].push_back({E[i].B, k - eps});
}
}
for(int i = m1 + 1; i <= m1 + m2; i++){
// A = k
double k = log2(E[i].k);
// 0 <= A - k
eg[E[i].A].push_back({0, - k});
// A <= 0 + k
eg[0].push_back({E[i].A, k});
}
ooo = 0;
while(!que.empty()) que.pop();
for(int i = 0; i <= n; i++) l[i] = 1e9, vis[i] = cnt[i] = 0;
for(int i = 0; i <= n; i++) Record(i, 0);
while(!que.empty()){
int i = que.front();
que.pop(), vis[i] = 0;
for(Edge e : eg[i]){
Record(e.first, e.second + l[i]);
}
}
return ooo ? 1 : 0;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m1 >> m2;
for(int i = 1; i <= m1; i++){
cin >> E[i].o >> E[i].A >> E[i].B >> E[i].k;
}
for(int i = 1; i <= m2; i++){
cin >> E[m1 + i].A >> E[m1 + i].k;
}
LL l = 1, r = 1e10;
while(l < r){
LL mid = (l + r + 1) >> 1;
if(check(mid / double(1e6))){
l = mid;
}else r = mid - 1;
}
if(!check(l / double(1e6))){
cout << -1;
return 0;
}
cout << fixed << setprecision(6) << l / double(1e6);
return 0;
}
CF1183F - Topforces Strikes Back
如果选择两个我们可以直接先选择最大值,为什么?因为 \(\frac{\max}{2} + \frac{\max}{3} \le max\)。
拓展一下,在三个中我们发现唯一的反例:\(\frac{\max}{2} + \frac{\max}{3} + \frac{\max}{5} = \frac{31}{30} \times \max \ge max\)。特判即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 2e5 + 3;
int n, a[MAXN];
multiset<int> st;
int main(){
ios::sync_with_stdio(0), cin.tie(0);
int T;
cin >> T;
while(T--){
cin >> n;
st.clear();
for(int i = 1; i <= n; i++){
cin >> a[i], st.insert(a[i]);
}
int MX = *st.rbegin();
int ans = MX;
if(MX % 2 == 0 && MX % 3 == 0 && MX % 5 == 0 && st.find(MX/2) != st.end() && st.find(MX/3) != st.end() && st.find(MX/5) != st.end()){
ans = max(ans, MX / 2 + MX / 3 + MX / 5);
}
for(int i = 1; i <= n; i++){
if(MX % a[i] == 0){
st.erase(st.find(a[i]));
}
}
if(!st.empty()){
int _MX = *st.rbegin();
ans = max(ans, MX + _MX);
for(int i = 1; i <= n; i++){
if(MX % a[i] > 0 && _MX % a[i] == 0){
st.erase(st.find(a[i]));
}
}
if(!st.empty()){
ans = max(ans, MX + _MX + *st.rbegin());
}
}
cout << ans << "\n";
}
return 0;
}
CF843D - Dynamic Shortest Path
如果每修改一次就 dij 复杂度 \(O(q (n + m \log n))\) 过不去的。
暴力 dij 是因为值域很大需要用到堆,带个 log,要是值域很小就可以直接分层 BFS 了……
每次增加的边权很小,求最短路增量?设 \(dis_i\) 表示这次修改前最短路,\(f_i\) 表示这次修改后最短路增量。
有 \(f_v = \min\limits_{(u,v) \in E}{dis_u + f_u + w(u,v) - dis_v}\)。
而每次修改后最大增量是小于等于 \(c\) 的,可以分层 BFS。
注意每一层可能由自己这一层转移来(因为边权为 0),所以每一层内部需要用队列。
复杂度 \(O(q(c + m + n))\)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e5 + 3;
struct Edge{ // 链式前向星 方便修改边权
int to, epre, w;
}eg[MAXN];
int egtop[MAXN], tot = 0;
int ADDeg(int u, int v, int val){
tot++, eg[tot].to = v, eg[tot].w = val;
eg[tot].epre = egtop[u], egtop[u] = tot;
return tot;
}
int n, m, Q, id[MAXN];
LL dis[MAXN], f[MAXN];
queue<int> p[MAXN];
void dij(){
for(int i = 1; i <= n; i++){
dis[i] = 1e18;
}
priority_queue<pair<LL, int>> pq;
dis[1] = 0, pq.push({0, 1});
while(!pq.empty()){
pair<LL, int> w = pq.top();
int i = w.second;
pq.pop();
if(dis[i] < -w.first) continue;
for(int e = egtop[i]; e > 0; e = eg[e].epre){
int nx = eg[e].to;
LL nw = dis[i] + eg[e].w;
if(dis[nx] > nw) dis[nx] = nw, pq.push({-nw, nx});
}
}
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m >> Q;
for(int i = 1, U, V, W; i <= m; i++){
cin >> U >> V >> W, id[i] = ADDeg(U, V, W);
}
dij();
for(int q = 1, op, c, v; q <= Q; q++){
cin >> op >> c;
if(op == 1){
cout << (dis[c] >= 1e18 ? -1 : dis[c]) << "\n";
}else{
for(int _c = 0; _c < c; _c++){
cin >> v, eg[id[v]].w++;
}
for(int i = 1; i <= n; i++) f[i] = c + 1;
f[1] = 0, p[0].push(1);
for(int d = 0; d <= c; d++){
while(!p[d].empty()){
int x = p[d].front();
p[d].pop();
if(f[x] < d) continue;
for(int e = egtop[x]; e > 0; e = eg[e].epre){
int nx = eg[e].to;
LL nw = dis[x] + f[x] + eg[e].w - dis[nx];
if(nw < f[nx]) f[nx] = nw, p[nw].push(nx);
}
}
}
for(int i = 1; i <= n; i++) dis[i] += f[i];
for(int d = 0; d <= c; d++){
while(!p[d].empty()) p[d].pop();
}
}
}
return 0;
}
luogu - P3403 跳楼机
考虑找到 \(0\) 能到达最低的 \(p\) 满足 \(p \bmod x = i\),可以跑最短路。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e5 + 3;
LL h, x, y, z;
LL dp[MAXN];
int main(){
cin >> h >> x >> y >> z;
priority_queue<pair<LL, int>> pq;
for(int i = 0; i < x; i++) dp[i] = -1;
dp[0] = 0, pq.push({0, 0});
while(!pq.empty()){
pair<LL, int> w = pq.top();
int i = w.second;
pq.pop();
if(dp[i] < -w.first) continue;
LL nx = (i + y) % x, nw = dp[i] + y;
if(dp[nx] == -1 || dp[nx] > nw) dp[nx] = nw, pq.push({-nw, nx});
nx = (i + z) % x, nw = dp[i] + z;
if(dp[nx] == -1 || dp[nx] > nw) dp[nx] = nw, pq.push({-nw, nx});
}
LL ans = 0;
h--;
for(int i = 0; i < x; i++){
if(dp[i] < 0 || dp[i] > h) continue;
ans = (ans + (h - dp[i]) / x + 1);
}
cout << ans;
return 0;
}
luogu - P2371 [国家集训队] 墨墨的等式
和跳楼机一样。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 5e5 + 3;
LL l, r;
int n, x, d[20];
LL dp[MAXN];
int main(){
cin >> n >> l >> r >> x;
for(int i = 1; i < n; i++){
cin >> d[i];
}
priority_queue<pair<LL, int>> pq;
for(int i = 0; i < x; i++) dp[i] = -1;
pq.push({0, 0}), dp[0] = 0;
while(!pq.empty()){
pair<LL, int> w = pq.top();
int i = w.second;
pq.pop();
if(dp[i] < -w.first) continue;
for(int h = 1; h < n; h++){
LL nx = (i + d[h]) % x, nw = dp[i] + d[h];
if(dp[nx] == -1 || dp[nx] > nw) dp[nx] = nw, pq.push({-nw, nx});
}
}
LL ans = 0;
l--;
for(int i = 0; i < x; i++){
if(dp[i] >= 0 && dp[i] <= r) ans = (ans + (r - dp[i]) / x + 1);
if(dp[i] >= 0 && dp[i] <= l) ans = (ans - (l - dp[i]) / x - 1);
}
cout << ans;
return 0;
}
CF986F - Oppa Funcan Style Remastered
可以转化为要给每个质因数配一个非负系数。
- 对于一个质因数,判断倍数关系。
- 对于两个质因数,exgcd 或 解方程 求解。
- 对于大于两个质因数,luogu - P2371 [国家集训队] 墨墨的等式 板子。
如果暴力分解 \(k\) 会太慢,优化:预处理每个质数的下一个质数。
注意 \(k=1\) 需要特判 NO
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
LL l, r;
int n, x, d[20];
vector<LL> p[53];
vector<LL> dp[53];
LL qpow(LL A, LL B, LL mod){
LL ret = 1;
while(B > 0){
if(B & 1) ret = ret * A % mod;
A = A * A % mod, B >>= 1;
}
return ret;
}
int nex[40000003];
bool vis[40000003];
int main(){
ios::sync_with_stdio(0), cin.tie(0);
int T, tot = 0;
cin >> T;
map<LL, int> mp;
for(int i = 2, la = 0; i <= 4e7; i++){
if(!vis[i]){
for(int j = i + i; j <= 4e7; j += i) vis[j] = 1;
nex[la] = i;
la = i;
}
}
while(T--){
LL N, k;
cin >> N >> k;
if(k == 1){
cout << "NO\n";
continue;
}
int id = 0;
if(mp.find(k) == mp.end()){
mp[k] = id = ++tot;
for(LL j = 2, ooo = 0; j * j <= k; j = nex[j]){
ooo = 0;
if(k % j == 0) p[tot].push_back(j), ooo = 1;
while(k % j == 0){
k /= j;
}
}
if(k > 1) p[tot].push_back(k);
if(p[tot].size() > 2){
priority_queue<pair<LL, int>> pq; // 预处理
int x = p[tot][0];
dp[tot].resize(x);
for(int i = 0; i < x; i++) dp[tot][i] = -1;
pq.push({0, 0}), dp[tot][0] = 0;
while(!pq.empty()){
pair<LL, int> w = pq.top();
int i = w.second;
pq.pop();
if(dp[tot][i] < -w.first) continue;
for(int h = 1; h < p[tot].size(); h++){
LL nx = (i + p[tot][h] % x) % x, nw = dp[tot][i] + p[tot][h];
if(dp[tot][nx] == -1 || dp[tot][nx] > nw) dp[tot][nx] = nw, pq.push({-nw, nx});
}
}
}
}else id = mp[k];
if(p[id].size() == 1){
cout << (N % p[id].back() == 0 ? "YES\n" : "NO\n");
continue;
}
if(p[id].size() == 2){
// a * x + b * y = N (mod a)
// b * y = N (mod a)
// y = N / b (mod a)
// (n / b) mod a * b <= N
int ans = 0;
LL a = p[id][0], b = p[id][1];
if(N % a == 0 || N % b == 0) ans = 1;
if(b * (qpow(b % a, a - 2, a) * (N % a) % a) <= N) ans = 1;
cout << (ans == 1 ? "YES\n" : "NO\n");
continue;
}
LL w = dp[id][N % p[id][0]];
cout << (w >= 0 && w <= N ? "YES\n" : "NO\n");
}
return 0;
}
/*
2
1863 2257
7 1533
NO
YES
14
312029972894833127 840189948895669
952769774260879484 282726514981201
608171586176169285 958115664994991
88623267497954796 219281243333749
274358699525645234 279844780167731
868154653722218363 811780512070093
50085164465918688 267349819256099
846087818801586210 72875781119861
870764119188136588 847046808548771
384855561687960343 921874025263129
385626107071133318 279844780167731
9158975683984797 277544717696509
923991035290189331 643758030495989
629344629314915409 978132065082373
*/
CF1830D - Mex Tree
所有路径只有三种权值:\(0,1,2\)
如果贪心骗分,交替染色的答案是多少?是 \(2 \cdot \frac{n(n + 1)}{2} - n - \sum{[w_i == 1]}\)。得到一个答案的一个下届。
如果全部路径权值都是 \(2\) (包含一个节点的路径权值为 \(1\)) 则答案为 \(2 \cdot \frac{n(n + 1)}{2} - n\)(尽管这达不到)。得到一个答案的一个上届。
如果存在一个大小大于 \(\sqrt{n}\) 的连通块,答案显然小于 \(2 \cdot \frac{n(n + 1)}{2} - n - \sum{[w_i == 1]}\)(因为上届减少一个 \(x(x > n)\),低于了下届,可以忽略)。
\(f_{i,j,0/1}\) 表示 \(i\) 子树内,包含 \(i\) 的连通块大小 \(j\),\(i\) 的染色为 \(0/1\)。
转移显然的,实现即在树上背包的基础上对于枚举上届与 \(\sqrt{n}\) 取 \(\min\)。复杂度 \(O(n\sqrt{n})\),具体证明可以根据树上背包复杂度的 不等式+分类讨论 证明。具体证明见:https://www.luogu.com.cn/article/0tohp8tw
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int B = 450, MAXN = 3e5 + 3;
int n;
vector<LL> f[MAXN][2];
vector<int> eg[MAXN];
int sz[MAXN];
void dfs(int x, int dad){
sz[x] = 1;
f[x][0].resize(2), f[x][1].resize(2);
f[x][0][1] = 1, f[x][1][1] = 0;
for(int nxt : eg[x]){
if(nxt == dad) continue;
dfs(nxt, x);
for(int l = f[x][0].size() + 1; l <= min(B, sz[x] + sz[nxt]) + 1; l++){
f[x][0].push_back(-1e18), f[x][1].push_back(-1e18);
}
for(int i = min(B, sz[x]); i >= 1; i--){
for(int j = 1; j <= sz[nxt] && j + i <= B; j++){
f[x][0][i + j] = max(f[x][0][i + j], f[x][0][i] + f[nxt][0][j] + 2ll * sz[x] * sz[nxt] - 1ll * i * j);
f[x][1][i + j] = max(f[x][1][i + j], f[x][1][i] + f[nxt][1][j] + 2ll * sz[x] * sz[nxt] - 2ll * i * j);
}
LL mx0 = -1e18, mx1 = -1e18;
for(int j = 1; j <= sz[nxt] && j <= B; j++){
mx0 = max(mx0, f[x][0][i] + f[nxt][1][j] + 2ll * sz[x] * sz[nxt]);
mx1 = max(mx1, f[x][1][i] + f[nxt][0][j] + 2ll * sz[x] * sz[nxt]);
}
f[x][0][i] = max(f[x][0][i], mx0);
f[x][1][i] = max(f[x][1][i], mx1);
}
sz[x] += sz[nxt];
vector<LL> ().swap(f[nxt][0]);
vector<LL> ().swap(f[nxt][1]);
}
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
int T;
cin >> T;
while(T--){
cin >> n;
for(int i = 1; i <= n; i++) f[i][0].clear(), f[i][1].clear(), eg[i].clear();
for(int i = 1, U, V; i < n; i++){
cin >> U >> V;
eg[U].push_back(V), eg[V].push_back(U);
}
dfs(1, 0);
LL ans = 0;
for(int i = 1; i <= min(B, sz[1]); i++){
ans = max({ans, f[1][0][i], f[1][1][i]});
}
cout << ans << "\n";
}
return 0;
}
MX - 简单修路题
题面
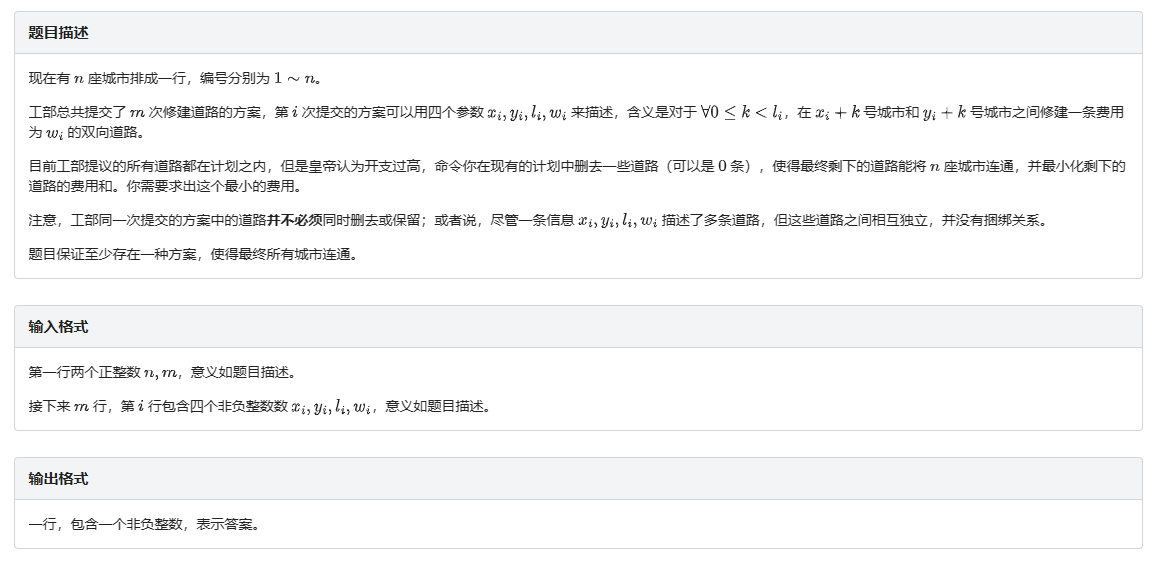
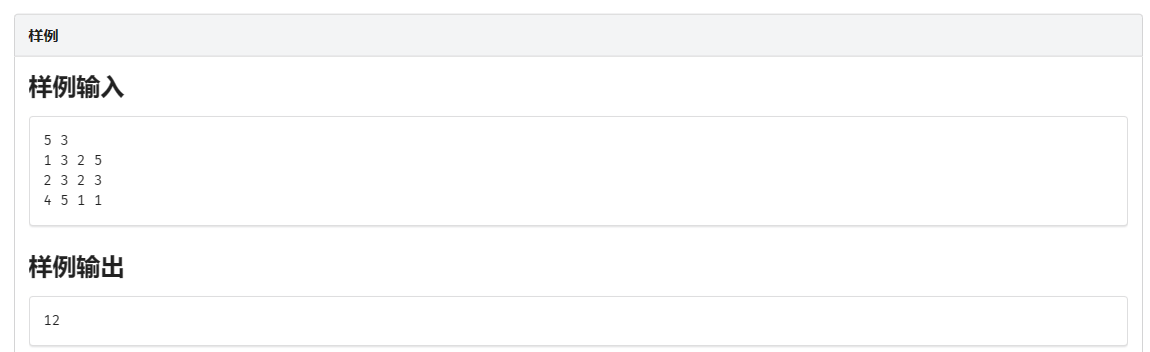
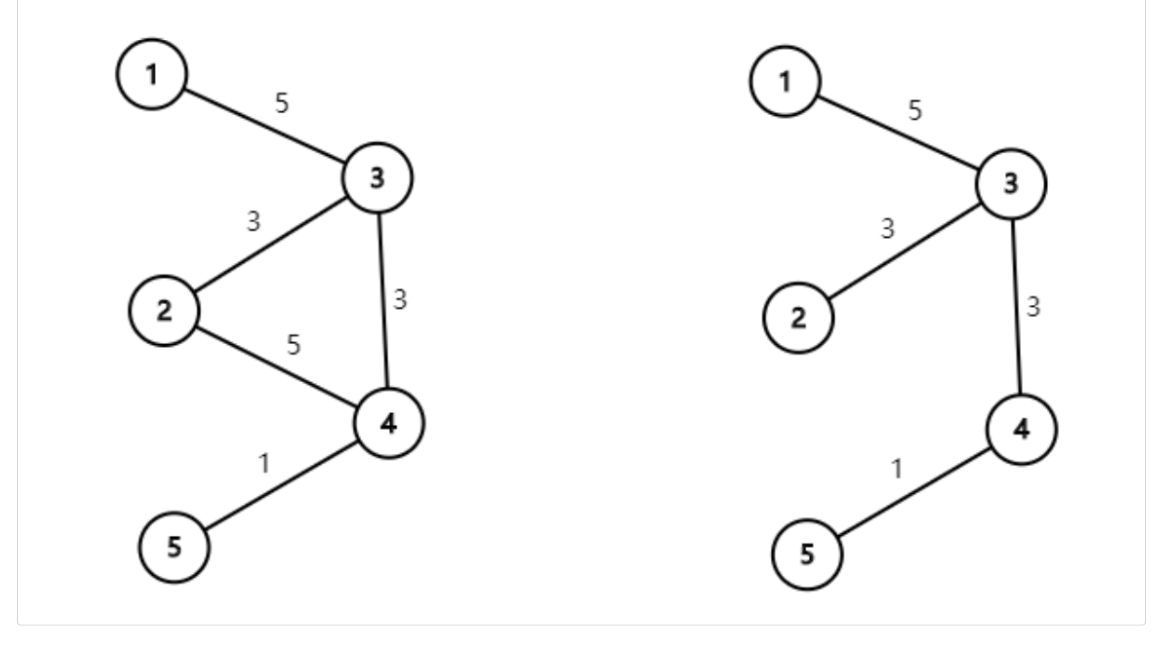

luogu - [SCOI2016] 萌萌哒 的强制在线版本。
如果这题用 kruska 就需要实现:在线的并查集区间合并。
可以用 ST 表,每个区间合并,如果这个区间没有全部合并就将子树分别合并。这样暴力做,因为合并次数最多 \(O(n)\),然后我们为了找到每次合并花费了 \(O(\log n \log n)\)(一个并查集,一个向子树枚举)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 5e5 + 3, MAXL = 20;
int LG(LL x){
int ret = 0;
while(x > 0) x >>= 1, ret++;
return ret;
}
struct Edge{
int x, y, l, w;
}E[MAXN];
LL ANS = 0;
int n, m;
int fa[MAXL][MAXN];
int Getf(int d, int x){ return fa[d][x] == x ? x : fa[d][x] = Getf(d, fa[d][x]); }
void Merge(int x, int y, int d, int w){
int fx = Getf(d, x), fy = Getf(d, y);
if(fx == fy) return;
fa[d][fx] = fy;
if(d == 0){
ANS += w;
return;
}
Merge(x, y, d - 1, w), Merge(x + (1ll << (d-1)), y + (1ll << (d-1)), d - 1, w);
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
freopen("road.in", "r", stdin);
freopen("road.out", "w", stdout);
cin >> n >> m;
for(int i = 1; i <= m; i++){
cin >> E[i].x >> E[i].y >> E[i].l >> E[i].w;
}
sort(E + 1, E + 1 + m, [](Edge i, Edge j){ return i.w < j.w; });
for(int d = 0; d < MAXL; d++) for(int i = 1; i <= n; i++) fa[d][i] = i;
for(int i = 1; i <= m; i++){
int lg = LG(E[i].l) - 1;
Merge(E[i].x, E[i].y, lg, E[i].w);
Merge(E[i].x + E[i].l - (1ll << lg), E[i].y + E[i].l - (1ll << lg), lg, E[i].w);
}
for(int i = 1; i <= n; i++){
if(Getf(0, i) != Getf(0, 1)){
cout << i << " &\n";
}
}
cout << ANS << "\n";
return 0;
}
MX - 西琳的魔法字符串
题面

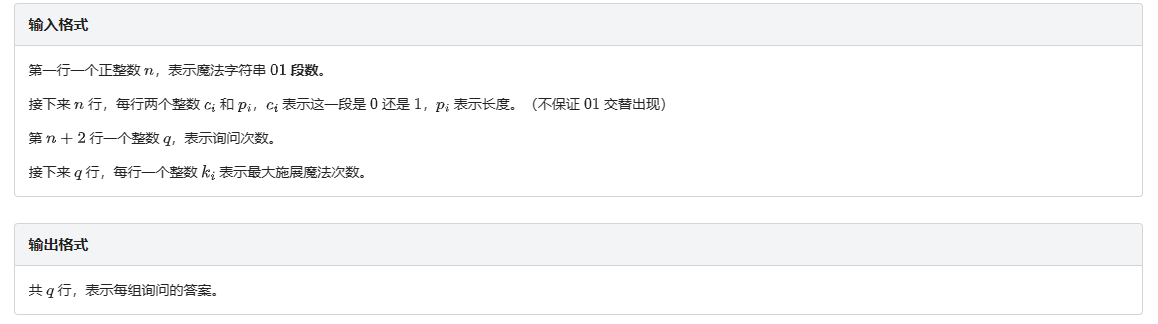
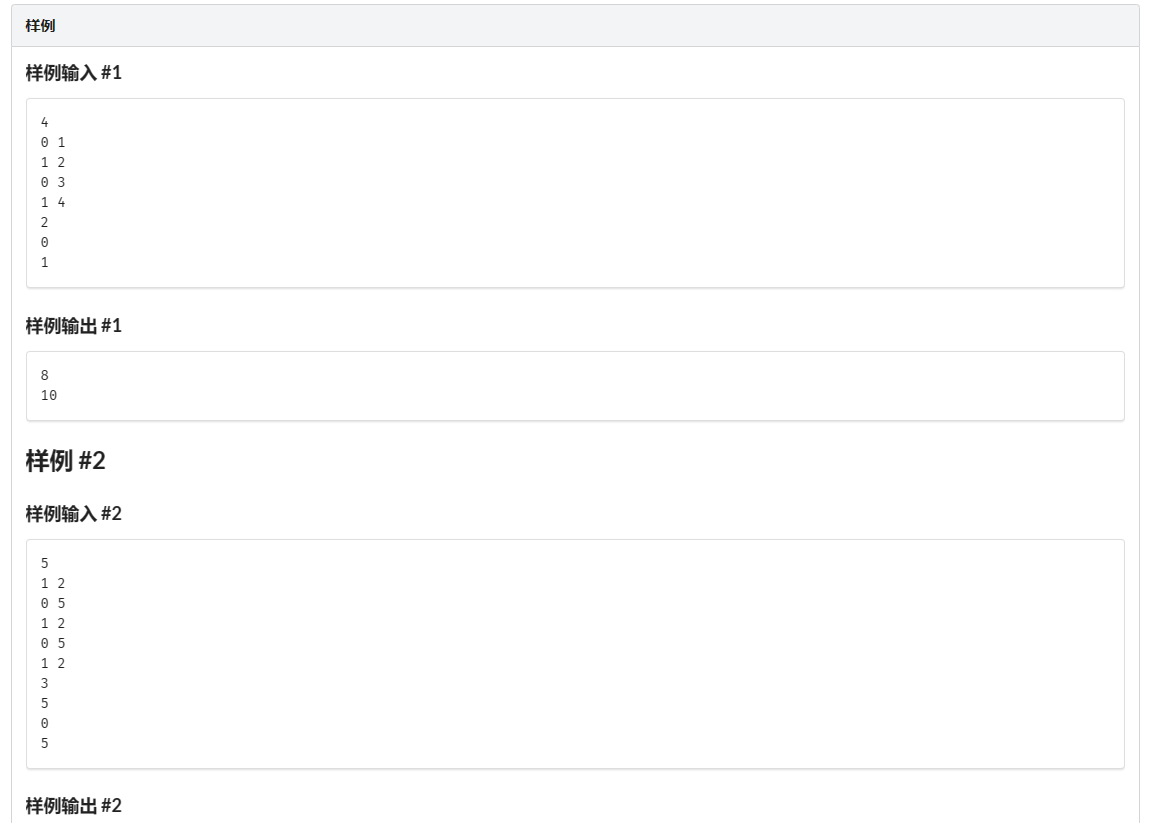
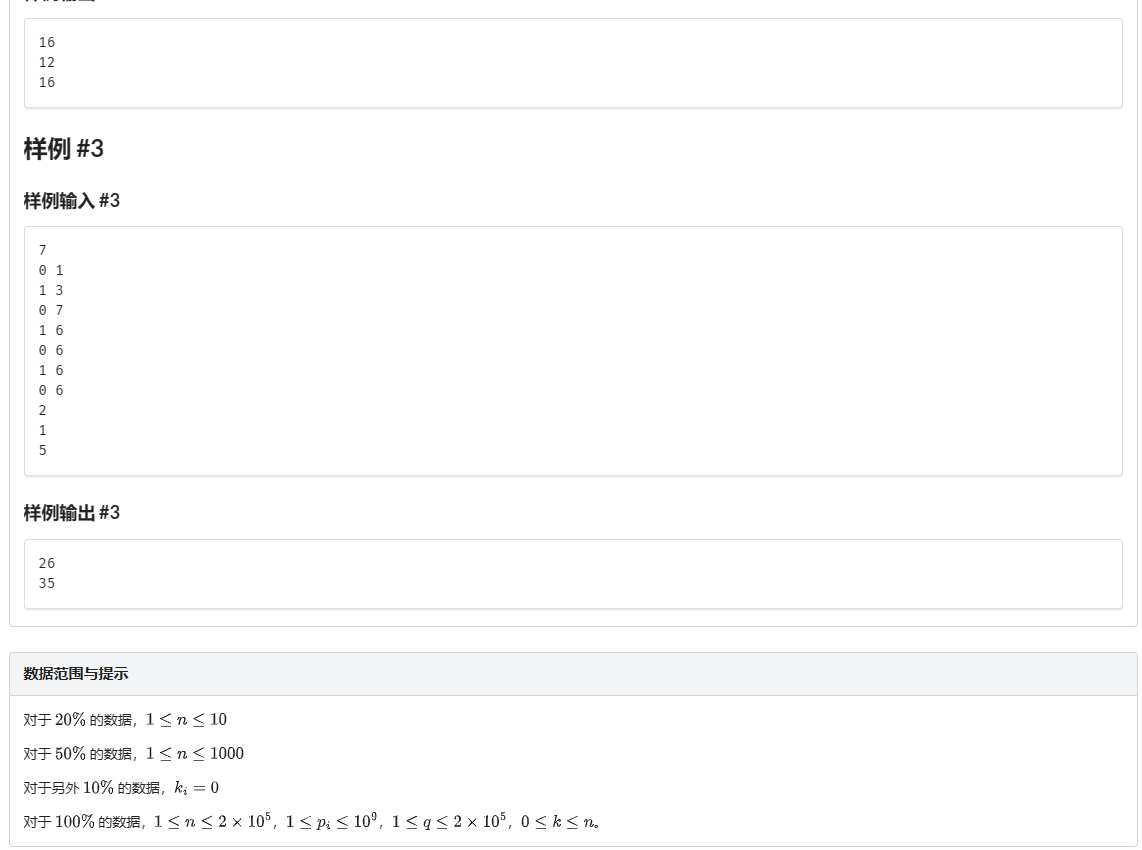
注意题目中的翻转是指 reverse
第一步:考虑算一个字符串的最长上升子序列
- \(s\) 表示 \(1\) 的个数。设每个 \(0\) 的权值为 \(1\),每个 \(1\) 的权值为 \(-1\),\(w_i\) 表示前缀权值之和。
- 答案为 \(s + \max{w_i}\)
第二步:转化翻转操作
- 可以当一个结论记,下次看到翻转应该想起来
- 翻转 \(k\) 次后取最大前缀,等价于,选择一个前缀 + 不超过 \(k\) 个互相不交的子段(当然也需要和选的前缀不交)
第三步:反悔贪心
- 选则 \(k\) 个不交子段有一种套路反悔贪心。
- 每次选择一个子段后,将子段中的值取反(这是正确的)。
第四步:数据结构
- 需要支持区间取反(乘 \(-1\)),并求最大子段和。线段树就可以了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 2e5 + 3;
struct SgTree{
LL sum, mx, pr, sf, P, S, ml, mr;
}tr[MAXN * 4][2];
int tag[MAXN * 4];
SgTree operator+ (SgTree i, SgTree j){
SgTree ret;
ret.sum = i.sum + j.sum;
if(i.pr < i.sum + j.pr) ret.pr = i.sum + j.pr, ret.P = j.P;
else ret.pr = i.pr, ret.P = i.P;
if(j.sf < j.sum + i.sf) ret.sf = j.sum + i.sf, ret.S = i.S;
else ret.sf = j.sf, ret.S = j.S;
if(i.mx > j.mx) ret.mx = i.mx, ret.ml = i.ml, ret.mr = i.mr;
else ret.mx = j.mx, ret.ml = j.ml, ret.mr = j.mr;
if(ret.mx < i.sf + j.pr) ret.mx = i.sf + j.pr, ret.ml = i.S, ret.mr = j.P;
return ret;
}
inline void Push(int i){ tag[i] ^= 1, swap(tr[i][0], tr[i][1]); }
inline void Merge(int i){ for(int o = 0; o < 2; o++) tr[i][o] = tr[i * 2][o] + tr[i * 2 + 1][o]; }
inline void Down(int i){ if(tag[i]) tag[i] = 0, Push(i * 2), Push(i * 2 + 1); }
int n, a[MAXN];
LL ans[MAXN];
void Build(int i, int l, int r){
tag[i] = 0;
if(l == r){
for(int o = 0; o < 2; o++){
if(o == 1) a[l] *= -1;
tr[i][o] = {a[l], a[l], a[l], a[l], l, l, l, l};
}
return;
}
int mid = (l + r) >> 1;
Build(i * 2, l, mid), Build(i * 2 + 1, mid + 1, r);
Merge(i);
}
void Update(int i, int l, int r, int L, int R){
if(l == L && r == R){
Push(i);
return;
}
int mid = (l + r) >> 1;
Down(i);
if(L <= mid) Update(i * 2, l, mid, L, min(mid, R));
if(mid + 1 <= R) Update(i * 2 + 1, mid + 1, r, max(mid + 1, L), R);
Merge(i);
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
freopen("end0.in", "r", stdin);
freopen("end0.out", "w", stdout);
cin >> n;
LL sss = 0;
for(int i = 1; i <= n; i++){
char ch; cin >> ch >> a[i];
if(ch == '1') a[i] *= -1, sss -= a[i];
}
Build(1, 1, n);
ans[0] = tr[1][0].pr, Update(1, 1, n, 1, tr[1][0].P);
for(int k = 1; k <= n; k++){
ans[k] = ans[k - 1] + tr[1][0].mx;
Update(1, 1, n, tr[1][0].ml, tr[1][0].mr);
}
for(int k = 1; k <= n; k++) ans[k] = max(ans[k], ans[k - 1]);
int Q, k;
cin >> Q;
while(Q--) cin >> k, cout << ans[k] + sss << "\n";
return 0;
}
CF297E - Mystic Carvings
题面意思:选择 3 个弦,然后标记 6 个点,如果这三条弦都满足两点之间最短路相同(标记的点权为 1,其余为 0),则方案合法,求选择方案数
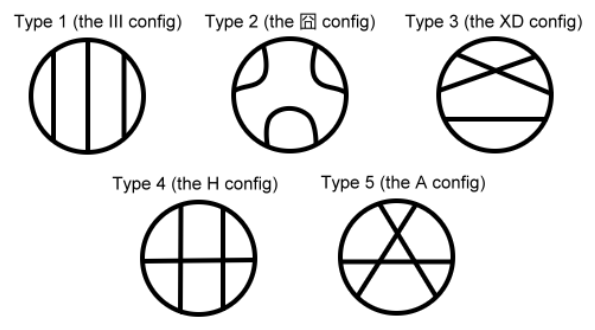
这题只有五种情况。发现其中合法的只有 2 和 5。但是如何算 2 和 5 都十分困难,想不好,考虑算其他不合法的 1、3、4。
对于 Type 1,枚举中间的边,然后算出左右两边的边数 \(l[i]\) 和 \(r[i]\)。
对于 Type 3 4,考虑如何合并两种情况。
共同满足:存在一条边,满足另外有一条与其相交、另外有一条与其分离。然后就可以直接根据 \(l[i]\) 和 \(r[i]\) 算了。
至于求 \(l[i],r[i]\) 可以分类讨论后转化为分类讨论算。
点击查看代码
/*
整体思路:不断化简题意
*/
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 2e5 + 3;
struct Node{
int x, y, l, r;
}a[MAXN];
int n;
int sum[MAXN];
void ADD(int x, int w){
for(; x <= 2 * n; x += (x & (-x))) sum[x] += w;
}
int QUE(int x){
int ret = 0;
for(; x > 0; x -= (x & (-x))) ret += sum[x];
return ret;
}
void Clear(){
for(int i = 1; i <= 2 * n; i++) sum[i] = 0;
}
void init(){
// 算 r
// x < X && Y < y
sort(a + 1, a + 1 + n, [](Node i, Node j){ return i.y < j.y; });
for(int i = 1, j = 1; i <= 2*n; i++){
vector<int> p;
while(j <= n && a[j].y == i){
a[j].r = QUE(2*n - a[j].x);
p.push_back(j), j++;
}
for(int x : p) ADD(2*n - a[x].x + 1, 1);
}
Clear();
// 算 l
// (X < x && Y < x) || (X > y && Y > y) || (X < x && Y > y)
// (Y < x) || (X > y) || (X < x && Y > y)
sort(a + 1, a + 1 + n, [](Node i, Node j){ return i.y > j.y; });
for(int i = 2*n, j = 1; i >= 1; i--){
vector<int> p;
while(j > 0 && a[j].y == i){
a[j].l = QUE(a[j].x - 1);
p.push_back(j), j++;
}
for(int x : p) ADD(a[x].x, 1);
}
Clear();
for(int i = 1; i <= n; i++) ADD(a[i].y, 1);
for(int i = 1; i <= n; i++) a[i].l += QUE(a[i].x - 1);
Clear();
for(int i = 1; i <= n; i++) ADD(2*n - a[i].x + 1, 1);
for(int i = 1; i <= n; i++) a[i].l += QUE(2*n - a[i].y);
Clear();
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for(int i = 1; i <= n; i++){
cin >> a[i].x >> a[i].y, a[i].l = a[i].r = 0;
if(a[i].x > a[i].y) swap(a[i].x, a[i].y);
}
init();
LL C = 1ll * n * (n - 1) * (n - 2) / 6, ans = 0, _ans = 0;
for(int i = 1; i <= n; i++){
LL l = a[i].l, r = a[i].r;
ans += l * r; // Type 1
_ans += 1ll * (n - l - r - 1) * (l + r); // Type 3 & Trpe 4
}
cout << C - ans - _ans / 2;
return 0;
}
[ABC134F] Permutation Oddness
试着往图论方向转化。最后发现这样一个图:
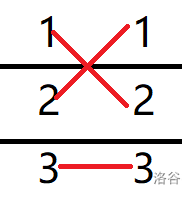
也就是二分图匹配,且每条边的边权为经过的黑线数量。
这样的好处是我们枚举到了第 \(i\) 条黑线,可以知道前面怪异度总和。
枚举前 \(i\) 条黑线,背上目前怪异度总和、还有多少个没有匹配。然后转移。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const LL mod = 1e9 + 7;
int n, K;
LL f[53][53][5003];
void ADD(LL &x, LL y){ x = (x + y) % mod; }
int main(){
cin >> n >> K;
ADD(f[0][0][0], 1);
for(int i = 0; i < n; i++){
for(int j = 0; j <= i; j++){
for(int k = 0; k <= K; k++){
ADD(f[i + 1][j + 1][k + 2*j], f[i][j][k]);
ADD(f[i + 1][j][k + 2*j], 2ll * f[i][j][k] % mod * j % mod + f[i][j][k]);
if(j > 0) ADD(f[i + 1][j - 1][k + 2*j], f[i][j][k] * j % mod * j % mod);
}
}
}
cout << f[n][0][K];
return 0;
}
CF1830F - The Third Grace
KTT 优化 dp。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 1e6 + 3;
const LL inf = 1e15;
LL w[MAXN], f[MAXN];
struct FC{
LL k, b;
FC operator+ (FC j) const { return {k + j.k, b + j.b}; }
void ADD(LL _k){ b += k * _k; }
};
pair<FC, LL> MAX(FC a, FC b){
if(a.k < b.k || (a.k == b.k && a.b < b.b)) swap(a, b);
if(a.b >= b.b) return {a, inf};
return {b, ((a.k - b.k) == 0 || (b.b - a.b) == 0 ? inf : (b.b - a.b) / (a.k - b.k))};
}
struct SgTree{
FC mx;
LL x;
SgTree operator+ (SgTree j) const {
SgTree i = {mx, x}, ret;
pair<FC, LL> tmp = MAX(i.mx, j.mx);
ret.x = min(i.x, j.x), ret.x = min(ret.x, tmp.second), ret.mx = tmp.first;
return ret;
}
};
struct KTT{
SgTree tr[MAXN * 4];
LL lz[MAXN * 4];
inline void Push(int i, LL k){
lz[i] += k, tr[i].x -= k, tr[i].mx.ADD(k);
}
inline void Down(int i){
if(lz[i]) Push(i * 2, lz[i]), Push(i * 2 + 1, lz[i]), lz[i] = 0;
}
void Force(int i, int l, int r, LL k){
if(k > tr[i].x){
int mid = (l + r) >> 1;
Force(i * 2, l, mid, k + lz[i]), Force(i * 2 + 1, mid + 1, r, k + lz[i]), lz[i] = 0;
tr[i] = tr[i * 2] + tr[i * 2 + 1];
}else Push(i, k);
}
void Update(int i, int l, int r, int L, int R, LL k){
if(l == L && r == R){
if(k == -1) tr[i].mx = {w[l], f[l]}, tr[i].x = inf;
else Force(i, l, r, k);
return;
}
int mid = (l + r) >> 1;
Down(i);
if(L <= mid) Update(i * 2, l, mid, L, min(mid, R), k);
if(mid + 1 <= R) Update(i * 2 + 1, mid + 1, r, max(mid + 1, L), R, k);
tr[i] = tr[i * 2] + tr[i * 2 + 1];
}
LL Query(int i, int l, int r, int L, int R){
if(l == L && r == R){
return tr[i].mx.b;
}
LL ret = 0;
int mid = (l + r) >> 1;
Down(i);
if(L <= mid) ret = max(ret, Query(i * 2, l, mid, L, min(mid, R)));
if(mid + 1 <= R) ret = max(ret, Query(i * 2 + 1, mid + 1, r, max(mid + 1, L), R));
return ret;
}
void Build(int i, int l, int r){
tr[i].x = inf, tr[i].mx = {0, 0}, lz[i] = 0;
if(l == r) return;
int mid = (l + r) >> 1;
Build(i * 2, l, mid), Build(i * 2 + 1, mid + 1, r);
}
}t;
int n, m;
vector<int> in[MAXN];
//mt19937 rnd(time(0));
void work(){
//n = 3, m = 5;
cin >> n >> m;
for(int i = 1; i <= m + 1; i++) in[i].clear();
for(int i = 1, l, r; i <= n; i++){
cin >> l >> r;
//l = rnd() % m + 1, r = rnd() % m + 1; if(l > r) swap(l, r);
in[r + 1].push_back(l);
}
for(int i = 1; i <= m; i++) cin >> w[i];
t.Build(1, 1, m);
for(int i = 1; i <= m + 1; i++){
for(int p : in[i]){
t.Update(1, 1, m, p, i - 1, 1);
}
if(i > 1) f[i] = t.Query(1, 1, m, 1, i - 1);
if(i > m) break;
t.Update(1, 1, m, i, i, -1);
}
cout << f[m + 1] << "\n";
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
int T = 500000; cin >> T;
while(T--) work();
return 0;
}
luogu - P5670 秘籍-反复异或
如果你想学指令集,就取看看 https://ouuan.github.io/post/n方过百万-暴力碾标算指令集优化的基础使用/ 注意这玩意 OI 中不能使用。
如果用 bitset 怎么做?
线段树,然后每个节点开一个 bitset 维护区间内每个元素出现的奇偶性。如果区间太小直接暴力做。
对于修改操作,也就是每个数对应到 \((i + x) \bmod 2^m\),bitset 可以直接位移实现。
关于线段树优化:对于区间大小小于 \(B\) 的节点,并不是对其不用 bitset,而是直接暴力算。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e5 + 3;
int B = 64;
bitset<1024> tr[MAXN * 4], tmp, ans, _tmp;
int n, _n, m, Q, a[MAXN], lz[MAXN * 4];
void Merge(int i, int len){
tr[i] = tr[i * 2] ^ tr[i * 2 + 1];
}
void Push(int i, int x, int l, int r, int L, int R){
if(R - L + 1 <= B){
tr[i].reset();
for(int j = l; j <= r; j++) a[j] = (a[j] + x) % m;
for(int j = L; j <= R; j++) tr[i].flip(a[j]);
}else tr[i] = (tr[i] << x) | (tr[i] >> (m - x)), tr[i] &= _tmp;
lz[i] = (lz[i] + x) % m;
}
void Down(int i, int l, int mid, int r){
if(lz[i]) Push(i * 2, lz[i], l, mid, l, mid), Push(i * 2 + 1, lz[i], mid+1, r, mid+1, r), lz[i] = 0;
}
void Build(int i, int l, int r){
if(r - l + 1 <= B){
Push(i, 0, l, r, l, r);
return;
}
int mid = (l + r) >> 1;
Build(i * 2, l, mid), Build(i * 2 + 1, mid + 1, r);
Merge(i, r - l + 1);
}
void Query(int i, int l, int r, int L, int R){
if(r - l + 1 <= B){
for(int x = max(l, L), y = min(r, R); x <= y; x++) ans.flip(a[x]);
return;
}
if(l == L && r == R){
ans = ans ^ tr[i];
return;
}
int mid = (l + r) >> 1;
Down(i, l, mid, r);
if(L <= mid) Query(i * 2, l, mid, L, min(mid, R));
if(mid + 1 <= R) Query(i * 2 + 1, mid + 1, r, max(mid + 1, L), R);
Merge(i, r - l + 1);
}
void Update(int i, int l, int r, int L, int R, int x){
if(r - l + 1 <= B){
Push(i, x, max(l, L), min(r, R), l, r);
return;
}
if(l == L && r == R){
Push(i, x, l, r, l, r);
return;
}
int mid = (l + r) >> 1;
Down(i, l, mid, r);
if(L <= mid) Update(i * 2, l, mid, L, min(mid, R), x);
if(mid + 1 <= R) Update(i * 2 + 1, mid + 1, r, max(mid + 1, L), R, x);
Merge(i, r - l + 1);
}
mt19937 rnd(time(0));
int main(){
ios::sync_with_stdio(0), cin.tie(0);
//n = 1e5, m = 10, Q = 1e5;
cin >> n >> m >> Q;
m = (1ll << m), _n = n;
for(int i = 1; i <= _n; i++){
//a[i] = rnd() % m;
cin >> a[i];
}
Build(1, 1, n);
for(int i = 0; i < m; i++) _tmp.flip(i);
for(int q = 1, op, l, r, x; q <= Q; q++){
//op = rnd() % 2 + 1;
//l = rnd() % _n + 1, r = rnd() % _n + 1;
//if(l > r) swap(l, r);
cin >> op >> l >> r;
if(op == 1){
//x = rnd() % m;
cin >> x;
Update(1, 1, n, l, r, x);
}else{
ans.reset(), Query(1, 1, n, l, r);
LL ANS = 0;
for(int i = 0; i < m; i++) if(ans[i]) ANS ^= i;
cout << ANS << "\n";
}
}
return 0;
}
luogu - P6680 [CCO2019] Marshmallow Molecules
也就是将 \(a\) 的所有儿子附加到 \(b\)(\(a\) 最靠前的儿子) 的儿子上,然后启发式合并就完了。利用了 STL 使用 swap 是 \(O(1)\) 的特性。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e5 + 3;
int n, m;
set<int> st[MAXN];
int main(){
cin >> n >> m;
for(int i = 1, x, y; i <= m; i++){
cin >> x >> y;
st[x].insert(y);
}
LL ans = 0;
for(int i = 1; i <= n; i++){
if(st[i].empty()) continue;
if(st[i].find(i) != st[i].end()) st[i].erase(st[i].find(i));
int nx = *st[i].begin();
ans += st[i].size();
if(st[i].size() > st[nx].size()) swap(st[i], st[nx]);
for(int x : st[i]) st[nx].insert(x);
}
cout << ans;
return 0;
}
luogu - P6681 [CCO2019] Bad Codes & qoj1193
首先考虑 dp。考虑两个串互相追逐的过程,然后就很容易得到状态设计,但是我们发现这个转移是有环的。
可以利用最短路算法优化 dp。注意这样的复杂度不是很高,因为 dijkstra 复杂度 \(O(n + m\log n)\) 中的 \(m\) 为松弛次数。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
struct Node{
int x, y;
LL w;
bool operator< (Node j) const {
return w > j.w;
}
};
int n, m;
string s[53];
LL dp[53][53];
priority_queue<Node> pq;
void ADD(LL w, int x, int y){
if(w < dp[x][y]){
dp[x][y] = w, pq.push({x, y, w});
}
}
int main(){
cin >> n >> m;
for(int i = 1; i <= n; i++){
cin >> s[i];
}
for(int i = 1; i <= n; i++){
for(int j = 0; j <= m; j++) dp[i][j] = 1e15;
}
for(int i = 1; i <= n; i++) ADD(s[i].size(), i, s[i].size());
while(!pq.empty()){
Node i = pq.top();
pq.pop();
if(dp[i.x][i.y] < i.w) continue;
for(int j = 1; j <= n; j++){
if(j == i.x && i.y == s[j].size()) continue; // 细节
if(s[j].size() >= i.y){
if(s[j].substr(0, i.y) == s[i.x].substr(s[i.x].size() - i.y, i.y)) ADD(i.w + s[j].size(), j, s[j].size() - i.y);
}else{
if(s[j] == s[i.x].substr(s[i.x].size() - i.y, s[j].size())) ADD(i.w + s[j].size(), i.x, i.y - s[j].size());
}
}
}
LL ans = 1e15;
for(int i = 1; i <= n; i++){
ans = min(ans, dp[i][0]);
}
cout << (ans >= 1e15 ? -1 : ans / 2);
return 0;
}
CF1085F - Rock-Paper-Scissors Champion
对于 R,发现如果左侧存在 S 和 P,S 一定可以击败 P。(如果 S 和 P 之间有 R,可以利用 P 消除 R。如果存在 P,也可以利用 P 消除 P)。
得到:如果左侧存在一个能击败 \(i\) 的,且左侧不存在能击败那个能击败 \(i\) 的,\(i\) 就一定无法获胜。右侧同理。
对于每一种手势,不能获胜的一定是两个区间的并集。(左右两边各一个)每次修改之后可以快速算出答案(用 set + 树状数组)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 2e5 + 3;
int n, Q;
int a[MAXN];
struct BIT{
int sum[MAXN];
void ADD(int x, int w){
for(; x <= n; x += (x & (-x))) sum[x] += w;
}
int QUE(int x){
int ret = 1;
for(; x > 0; x -= (x & (-x))) ret += sum[x];
return ret;
}
int Get(int l, int r){
if(l > r) return 0;
return QUE(r) - QUE(l - 1);
}
}s[3];
set<int> st[3];
int COL(char ch){
return (ch == 'R' ? 0 : (ch == 'S' ? 1 : 2));
}
int Get_ans(int op){
int f = (op - 1 + 3) % 3, _f = (op + 1) % 3;
int l = 1, r = 0, L = 1, R = 0;
if(!st[f].empty()){
l = *st[f].begin();
auto it = st[_f].lower_bound(l);
if(it != st[_f].begin()){
r = l - 1;
}else r = (it == st[_f].end() ? n : *it - 1);
}
if(!st[f].empty()){
R = *st[f].rbegin();
auto it = st[_f].upper_bound(R);
if(it != st[_f].end()){
L = R + 1;
}else L = (it == st[_f].begin() ? 1 : *prev(it) + 1);
}
return s[op].Get(l, r) + s[op].Get(L, R) - s[op].Get(max(l, L), min(r, R));
}
int ANS(){ return n - Get_ans(2) - Get_ans(1) - Get_ans(0); }
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> Q;
for(int i = 1; i <= n; i++){
char ch; cin >> ch; a[i] = COL(ch);
s[a[i]].ADD(i, 1), st[a[i]].insert(i);
}
cout << ANS() << "\n";
for(int q = 1; q <= Q; q++){
int i; char ch; cin >> i >> ch;
s[a[i]].ADD(i, -1), st[a[i]].erase(i);
a[i] = COL(ch);
s[a[i]].ADD(i, 1), st[a[i]].insert(i);
cout << ANS() << "\n";
}
return 0;
}
luogu - P1399 [NOI2013] 快餐店
就是求基环树上的直径。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 2e5 + 3;
int n, d[MAXN], S;
LL sum[MAXN], la[MAXN], nx[MAXN], lamx[MAXN], nxmx[MAXN];
LL dep[MAXN], _dep[MAXN], ans = 0, _ans = 1e18;
vector<PII> eg[MAXN], vt;
void dfs(int x, int w){
if(d[x] <= 1) return;
d[x] = 0, vt.push_back({x, w});
bool ooo = 0;
for(PII e : eg[x]){
if(d[e.first] > 1) dfs(e.first, e.second), ooo = 1;
}
if(ooo == 0){
for(PII e : eg[S]){
if(e.first == x) vt[0].second = e.second;
}
}
}
void work(int i, int nxt, LL w){
LL len = dep[nxt] + w;
if(dep[i] <= len){
swap(dep[i], _dep[i]), dep[i] = len;
}else if(_dep[i] <= len){
_dep[i] = len;
}
ans = max(ans, dep[i] + _dep[i]);
}
int main(){
//freopen("P1399_2.in", "r", stdin);
cin >> n;
for(int i = 1, U, V, W; i <= n; i++){
cin >> U >> V >> W, d[U]++, d[V]++;
eg[U].push_back({V, W}), eg[V].push_back({U, W});
}
queue<int> que;
for(int i = 1; i <= n; i++){
if(d[i] <= 1) que.push(i);
}
while(!que.empty()){
int i = que.front();
que.pop();
for(PII e : eg[i]){ int nxt = e.first;
if(d[nxt] <= 1){
work(i, nxt, e.second);
}else{
d[nxt]--;
if(d[nxt] <= 1) que.push(nxt);
}
}
}
for(int i = 1; i <= n; i++){
if(d[i] <= 1) continue;
for(PII e : eg[i]){
if(d[e.first] <= 1) work(i, e.first, e.second);
}
S = i;
}
dfs(S, 0);
multiset<LL> st;
sum[0] = vt[0].second;
for(int i = 1; i < vt.size(); i++) sum[i] = sum[i - 1] + vt[i].second;
lamx[0] = sum[0] + dep[vt[0].first];
for(int i = 0; i < vt.size(); i++){
if(i > 0) lamx[i] = max(lamx[i - 1], sum[i] + dep[vt[i].first]);
if(i > 0) la[i] = max(la[i - 1], *st.rbegin() + sum[i] + dep[vt[i].first]);
st.insert(- sum[i] + dep[vt[i].first]);
}
st.clear();
for(int i = vt.size() - 1; i >= 0; i--){
nxmx[i] = max(nxmx[i + 1], sum[vt.size() - 1] - sum[i] + dep[vt[i].first]);
if(i < vt.size() - 1) nx[i] = max(nx[i + 1], *st.rbegin() - sum[i] + dep[vt[i].first]);
st.insert(sum[i] + dep[vt[i].first]);
}
for(int i = 0; i < vt.size(); i++){
_ans = min(_ans, max({ans, (i == vt.size() - 1 ? 0ll : lamx[i] + nxmx[i + 1]), la[i], nx[i + 1]}));
}
cout << fixed << setprecision(1);
cout << _ans / 2.0;
return 0;
}
CF48G - Galaxy Union
简化题意:给定一个基环树(带边权),求每个点到其他点的距离之和。
基环树,常见套路是先找到环,对于每个环看作一个根,分别算子树内和环上。
实现可以利用拓扑排序(找环的同时进行 dp 转移)。
这题的前缀和需要拆式子。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 2e5 + 3;
int n, d[MAXN], fa[MAXN];
vector<PII> eg[MAXN], p;
LL sumw[MAXN], sums[MAXN], sum[MAXN];
LL dp[MAXN], sz[MAXN], dd[MAXN], ans[MAXN];
void dfs(int x, int dad){ // 换根 dp
fa[x] = fa[dad];
for(PII e : eg[x]){ int nxt = e.first;
if(nxt != dad && d[nxt] <= 1){
dd[nxt] = dd[x] + e.second;
dp[nxt] = (dp[x] + (sz[fa[x]] - sz[nxt]) * e.second - sz[nxt] * e.second);
dfs(nxt, x);
}
}
}
void Calc(){ // 判环
vector<int> stk;
for(int i = 1; i <= n; i++){
sz[i] = 1;
if(d[i] <= 1) stk.push_back(i);
}
while(!stk.empty()){
int x = stk.back();
stk.pop_back();
for(PII e : eg[x]){ int nxt = e.first;
if(d[nxt] <= 1) continue;
dp[nxt] += dp[x] + sz[x] * e.second, sz[nxt] += sz[x], d[nxt]--;
if(d[nxt] == 1) stk.push_back(nxt);
}
}
for(int i = 1; i <= n; i++){
if(d[i] > 1){
fa[0] = i, dd[i] = 0, dfs(i, 0);
}
}
}
LL C(int x, int y){
if(x <= y){
if(y == 0) return 0;
return sum[y-1] - (x>0?sum[x-1]:0);
}
return sum[p.size()-1] - sum[x-1] + (y>0?sum[y-1]:0);
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for(int i = 1, U, V, W; i <= n; i++){
cin >> U >> V >> W, eg[U].push_back({V, W}), eg[V].push_back({U, W}), d[U]++, d[V]++;
}
Calc();
int m = 0;
p.push_back({0, 0});
for(int i = 1; i <= n; i++){
if(d[i] > 1){
int x = i, y = -1, E = 0;
while(d[x] > 1){
d[x] = 1, p.push_back({x, 0}), m++, y = -1;
for(PII e : eg[x]) if(d[e.first] > 1){ p.back().second = e.second, y = e.first; break; }
if(y < 0) break;
x = y;
}
for(PII e : eg[x]) if(e.first == i){ p.back().second = e.second; break; }
break;
}
}
for(int i = 1; i <= m; i++) p.push_back(p[i]);
// \sum_{l+1}^{j}{ sz[i] * (sums[i-1] - sums[l-1])
// \sum_{j+1}^{h}{ sz[i] * (sums[h] - sums[i-1])
for(int i = 1; i <= 2 * m; i++){
sums[i] = sums[i - 1] + p[i].second;
sumw[i] = sumw[i - 1] + sz[p[i].first];
sum[i] = sum[i - 1] + sz[p[i].first] * sums[i-1];
}
LL S = sums[m], _S = 0, __S = 0;
for(int i = 1, j = 1; i <= m; i++){
_S += dp[p[i].first];
while(sums[j] - sums[i - 1] <= S / 2) j++;
int h = i + m - 1;
ans[p[i].first] = sum[j] - sum[i] - sums[i - 1] * (sumw[j] - sumw[i]);
ans[p[i].first] += sums[h] * (sumw[h] - sumw[j]) - sum[h] + sum[j];
}
for(int i = 1; i <= n; i++){
cout << ans[fa[i]] + _S - dp[fa[i]] + dp[i] + dd[i] * (n - sz[fa[i]]) << " ";
}
return 0;
}
CF1592E - Bored Bakry
如果需要 位于和 严格大于 异或和,则必须存在最高位大于。
我们需要找一个长度为偶数且每一个值的最高位相同,的子串。为什么是偶数?因为如果是奇数,则异或和这意味也是 1,不满足。
我们只需要确定最高位,然后限制异或和的更高位全为 \(0\)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e6 + 3;
int n, a[MAXN], s[MAXN], _s[MAXN];
map<int, int> mp[2];
int main(){
cin >> n;
for(int i = 1; i <= n; i++){
cin >> a[i], _s[i] = _s[i - 1] ^ a[i];
}
int ans = 0;
for(int h = 0; h <= 20; h++){
for(int i = 0; i <= n; i++) s[i] = _s[i] >> (h + 1);
for(int i = 1, j = 0; i <= n; i = j + 1){
j = i;
if((a[i] >> h) % 2 == 0) continue;
while(j + 1 <= n && (a[j + 1] >> h) % 2 == 1) j++;
mp[0].clear(), mp[1].clear();
for(int x = i; x <= j; x++){
if(mp[(x-1)&1].find(s[x - 1]) == mp[(x-1)&1].end()) mp[(x-1)&1][s[x - 1]] = x;
if(mp[x&1].find(s[x]) != mp[x&1].end()) ans = max(ans, x - mp[x&1][s[x]] + 1);
}
}
}
cout << ans;
return 0;
}
CF1854E - Game Bundles
对于大于 \(30\) 的元素,不会在选择的子序列中出现超过两次。
然后就不会做了?那就考虑随机化。
我们随机 \(a_i \le 30\) 的元素,然后一个一个选择大于 \(30\) 的元素。如果一次随机不行,我们就随机改变随机范围。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PLI = pair<LL, int>;
LL m;
LL f[63], _f[63];
vector<int> a;
mt19937_64 rnd(time(0));
bool Doit(int lim){
LL _m = m;
for(int i = 1; i <= 60; i++) f[i] = 0;
a.clear(), f[0] = 1;
while(1){
int x = rnd() % lim + 1;
for(int i = 0; i <= 60; i++) _f[i] = 0;
for(int i = 0; i <= 60; i++){
_f[i] += f[i];
if(i + x > 60) continue;
_f[i + x] += f[i];
}
if(_f[60] > m) break;
a.push_back(x);
for(int i = 0; i <= 60; i++) f[i] = _f[i];
}
m -= f[60];
vector<PLI> vt;
for(int i = 31; i <= 60; i++){
vt.push_back({f[60 - i], i});
}
sort(vt.begin(), vt.end(), [](PLI i, PLI j){ return i > j; });
for(PLI p : vt){
if(p.first == 0) break;
while(m - p.first >= 0){
m -= p.first, a.push_back(p.second);
}
}
if(m > 0 || a.size() > 60){
m = _m;
return 1;
}
cout << a.size() << "\n";
for(int x : a) cout << x << " ";
exit(0);
}
int main(){
cin >> m;
while(Doit(rnd() % 30 + 1));
return 0;
}
CF48D - Permutations
简单的构造题。这题主要难度就是不能被样例干扰。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PLI = pair<LL, int>;
const int MAXN = 1e5 + 3;
int n, a[MAXN], b[MAXN], ans[MAXN];
int main(){
cin >> n;
for(int i = 1; i <= n; i++){
cin >> a[i];
ans[i] = ++b[a[i]];
}
for(int i = 2; i <= 100000; i++){
if(b[i - 1] < b[i]){
cout << -1;
return 0;
}
b[i] = min(b[i - 1], b[i]);
}
cout << b[1] << "\n";
for(int i = 1; i <= n; i++){
cout << ans[i] << " ";
}
return 0;
}
CF48H - Black and White
大概这样填(其中 . 表示不确定方向的两色砖块):
BBBBBB
BBBB..
....WW
WWWWWW
WW....
......
或
BBBBBB
BBBB..
....WW
W.....
但是方向如何确定?暴力分类讨论显然难写。看代码,有一种省下很多分类讨论的方法。
代码非常短,不超过 60 行。关于字符串表示 \ 可以看看 https://www.cnblogs.com/huangqixuan/p/18349684#字符表示
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int dx[9] = {-1, 0, 1, 0};
const int dy[9] = {0, 1, 0, -1};
const string str[9] = {"", "####", "....", "#//.", "\\#.\\", ".//#", "\\.#\\"};
const string col[9] = {"", "####", "....", "#..#", "##..", ".##.", "..##"}; // 上右下左
const int MAXN = 103;
int n, m, a, b, c;
int vis[MAXN][MAXN];
bool check(int x, int y){
for(int h = 0; h < 4; h++){
int nx = dx[h] + x, ny = dy[h] + y;
if(nx > 0 && ny > 0 && nx <= n && ny <= m && vis[nx][ny] > 0){
if(col[vis[x][y]][h] != col[vis[nx][ny]][(h + 2) % 4]) return 0;
}
}
return 1;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
cin >> a >> b >> c;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
if(a > 0){
vis[i][j] = 1, a--;
}else if(b > 0 && vis[i-1][j] != 1 && vis[i][j-1] != 1 && vis[i+1][j] != 1 && vis[i][j+1] != 1){
vis[i][j] = 2, b--;
}else vis[i][j] = 0;
}
}
for(int i = 1; i <= n; i++){
vector<int> p;
bool ooo = 0;
for(int j = 1; j <= m; j++){
if(vis[i][j] == 0) p.push_back(j);
if(vis[i][j] == 2 && !ooo) ooo = 1, reverse(p.begin(), p.end());// 这一步剩下了大量分类讨论
}
for(int x : p){
vis[i][x] = 3;
while(!check(i, x)) vis[i][x]++;
}
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++) cout << str[vis[i][j]][0] << str[vis[i][j]][1];
cout << "\n";
for(int j = 1; j <= m; j++) cout << str[vis[i][j]][2] << str[vis[i][j]][3];
cout << "\n";
}
return 0;
}
luogu - P5532 [CCO2019] Sirtet
考虑求每个连通块需要下降的长度。首先考虑单独一列:
#
.
#
.
.
#
.
考虑向下连边,如果下面是 # 就边权为 \(0\),否则为 \(1\)。然后就是求到最下面的路径长度。
如果是连通块,则下降的长度就是每个点下降长度的最小值,连通块之间连边边权 \(0\) 就可以了。然后跑最短路(使用 01-BFS)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 1e6 + 3;
const int dx[9] = {0, 0, 1, -1};
const int dy[9] = {1, -1, 0, 0};
int H, W, n, dp[MAXN];
char ch[MAXN];
vector<PII> eg[MAXN];
bool vis[MAXN];
int Ri(int x, int y){ return (x-1) * W + y; }
void dfs(int i, int j){
vis[Ri(i, j)] = 1;
for(int h = 0; h < 4; h++){
int nx = i + dx[h], ny = j + dy[h];
if(nx > 0 && ny > 0 && nx <= H && ny <= W && ch[Ri(nx, ny)] == '#' && !vis[Ri(nx, ny)]){
eg[Ri(i, j)].push_back({Ri(nx, ny), 0}), eg[Ri(nx, ny)].push_back({Ri(i, j), 0});
dfs(nx, ny);
}
}
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> H >> W, n = H * W;
for(int i = 1; i <= H; i++){
for(int j = 1; j <= W; j++){
cin >> ch[Ri(i, j)];
}
}
for(int i = 1; i <= H; i++){
for(int j = 1; j <= W; j++){
if(ch[Ri(i, j)] == '#' && vis[Ri(i, j)] == 0) dfs(i, j);
if(i == H || ch[Ri(i + 1, j)] == ch[Ri(i, j)] && ch[Ri(i, j)] == '#') continue;
eg[Ri(i + 1, j)].push_back({Ri(i, j), (ch[Ri(i + 1, j)] == '.')});
}
}
deque<int> que;
for(int i = 1; i <= n; i++) dp[i] = 1e9;
for(int j = 1; j <= W; j++) que.push_back(Ri(H, j)), dp[Ri(H, j)] = 0;
while(!que.empty()){
int i = que.front();
que.pop_front();
for(PII e : eg[i]){
if(dp[e.first] > dp[i] + e.second){
dp[e.first] = dp[i] + e.second;
if(!e.second) que.push_front(e.first);
else que.push_back(e.first);
}
}
}
vector<vector<char>> ans(H+3, vector<char>(W+3, '.'));
for(int i = 1; i <= H; i++){
for(int j = 1; j <= W; j++){
if(ch[Ri(i, j)] == '#') ans[i + dp[Ri(i, j)]][j] = '#';
}
}
for(int i = 1; i <= H; i++){
for(int j = 1; j <= W; j++){
cout << ans[i][j];
}
cout << "\n";
}
return 0;
}
luogu - P4256 公主の#19准备月考
显然可以维护质因数出现次数,但是直接存 25 个元素太慢了。
注意到值域 \([1,100]\),除 \(2,3,5,7\) 以外的质因数的出现次数不超过一。所以可以压位,然后只用存 5 个元素。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 3e5 + 3;
const int pr[30] = {11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97};
int pr_mp[100];
struct Node{
int a[5];
// 0->2 1->3 2->5 3->7 4->.
Node operator+ (Node j) const { Node ret;
for(int i = 0; i < 4; i++) ret.a[i] = max(a[i], j.a[i]);
ret.a[4] = a[4] | j.a[4];
return ret;
}
Node operator- (Node j) const { Node ret;
for(int i = 0; i < 4; i++) ret.a[i] = min(a[i], j.a[i]);
ret.a[4] = a[4] & j.a[4];
return ret;
}
}trmx[MAXN * 4], trmi[MAXN * 4], lz[MAXN * 4], tmp, zero, inf;
int n, Q;
Node read(){
int x; cin >> x;
Node ret = zero;
for(int i = 2; i * i <= x; i++){
while(x % i == 0){
x /= i;
if(i == 2) ret.a[0]++;
if(i == 3) ret.a[1]++;
if(i == 5) ret.a[2]++;
if(i == 7) ret.a[3]++;
if(i > 7) ret.a[4] |= (1ll << pr_mp[i]);
}
}
if(x > 1){
if(x == 2) ret.a[0]++;
if(x == 3) ret.a[1]++;
if(x == 5) ret.a[2]++;
if(x == 7) ret.a[3]++;
if(x > 7) ret.a[4] |= (1ll << pr_mp[x]);
}
return ret;
}
inline void Push(int i, Node w){ lz[i] = w, trmi[i] = trmx[i] = w; }
inline void Merge(int i){ trmx[i] = trmx[i*2] + trmx[i*2+1], trmi[i] = trmi[i*2] - trmi[i*2+1]; }
inline void Down(int i){
if(lz[i].a[0] >= 0) Push(i * 2, lz[i]), Push(i * 2 + 1, lz[i]), lz[i].a[0] = -1;
}
void Build(int i, int l, int r){
lz[i].a[0] = -1;
if(l == r){
trmx[i] = trmi[i] = read();
return;
}
int mid = (l + r) >> 1;
Build(i * 2, l, mid), Build(i * 2 + 1, mid + 1, r), Merge(i);
}
void Update(int i, int l, int r, int L, int R){
if(l == L && r == R){
Push(i, tmp);
return;
}
int mid = (l + r) >> 1;
Down(i);
if(L <= mid) Update(i * 2, l, mid, L, min(mid, R));
if(mid + 1 <= R) Update(i * 2 + 1, mid + 1, r, max(mid + 1, L), R);
Merge(i);
}
int opt = 0;
void Query(int i, int l, int r, int L, int R){
//cout << i << " " << l << " " << r << " " << L << " " << R << "\n";
if(l == L && r == R){
if(opt == 1) tmp = tmp + trmx[i];
if(opt == 2) tmp = tmp - trmi[i];
return;
}
int mid = (l + r) >> 1;
Down(i);
if(L <= mid) Query(i * 2, l, mid, L, min(mid, R));
if(mid + 1 <= R) Query(i * 2 + 1, mid + 1, r, max(mid + 1, L), R);
Merge(i);
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
inf.a[4] = (1ll << 21) - 1, zero.a[4] = 0;
for(int i = 0; i < 4; i++) inf.a[i] = 9, zero.a[i] = 0;
for(int i = 0; i < 21; i++) pr_mp[pr[i]] = i;
pr_mp[0] = 2, pr_mp[1] = 3, pr_mp[2] = 5, pr_mp[3] = 7;
cin >> n >> Q;
Build(1, 1, n);
for(int q = 1, l, r; q <= Q; q++){
char ch; cin >> ch >> l >> r;
if(ch == 'C'){
tmp = read(), Update(1, 1, n, l, r);
}else if(ch == 'L'){
tmp = zero, opt = 1, Query(1, 1, n, l, r);
}else if(ch == 'G'){
tmp = inf, opt = 2, Query(1, 1, n, l, r);
}else{
tmp = inf, opt = 2, Query(1, 1, n, l, r);
}
if(ch != 'C'){
LL mod;
cin >> mod;
if(ch == 'S'){
LL ans = 1 % mod, cnt = 0;
for(int i = 0; i < 4; i++) cnt += tmp.a[i], ans = ans * (tmp.a[i] + 1) % mod;
for(int i = 0; i < 21; i++) if((tmp.a[4] >> i) & 1) cnt++, ans = ans * 2ll % mod;
cout << ans << "\n";
}else{
LL ans = 1 % mod, cnt = 0;
for(int i = 0; i < 4; i++) while(tmp.a[i] > 0) cnt++, tmp.a[i]--, ans = ans * pr_mp[i] % mod;
for(int i = 0; i < 21; i++) if((tmp.a[4] >> i) & 1) cnt++, ans = ans * pr[i] % mod;
cout << ans << "\n";
}
}
}
return 0;
}
[ABC260F] Find 4-cycle
枚举题。主要利用 只要求找一个解 这个性质。
对于每个左侧点,暴力枚举右侧点对,如果一个点对第二次跟新,则输出答案。
每个左侧点对被枚举至多一次,复杂度 \(O(T^2)\)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 4e5 + 3;
int S, T, m;
vector<int> eg[MAXN];
int f[3003][3003];
int main(){
cin >> S >> T >> m;
for(int i = 1, U, V; i <= m; i++){
cin >> U >> V, eg[U].push_back(V);
}
for(int i = 1; i <= S; i++){
for(int x = 0; x < eg[i].size(); x++){
for(int y = x + 1; y < eg[i].size(); y++){
int X = eg[i][x], Y = eg[i][y];
if(X > Y) swap(X, Y);
X -= S, Y -= S;
if(f[X][Y]){
cout << X + S << " " << i << " " << Y + S << " " << f[X][Y];
return 0;
}
f[X][Y] = i;
}
}
}
cout << -1;
return 0;
}
CF436F - Tree Array
期望是可以拆分开的,我们考虑每个逆序对的贡献。
首先枚举出根节点。每个逆序对有两种情况,如果是先祖关系则一定是贡献一,接下来考虑第二种情况。
设两点最接近选择的点的距离为 \(x,y\)。任意时刻选择了 \(lca\),则我们有 \(\frac{1}{2}\) 的概率 \(x-1\) 否则 \(y-1\)(不需要考虑两个都不变化的时候)。然后预处理即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using i128 = __int128_t;
const LL mod = 1e9 + 7;
const int MAXN = 200 + 3;
LL qpow(LL A, LL B){
LL ret = 1;
while(B > 0){
if(B & 1) ret = ret * A % mod;
A = A * A % mod, B >>= 1;
}
return ret;
}
int n;
vector<int> eg[MAXN], son[MAXN];
LL f[MAXN][MAXN], ans = 0;
int dep[MAXN];
void dfs(int x, int dad){
dep[x] = dep[dad] + 1, son[x].clear();
for(int nxt : eg[x]){
if(nxt == dad) continue;
dfs(nxt, x);
for(int y : son[nxt]){
for(int z : son[x]){
int X = y, Y = z;
if(X < Y) swap(X, Y);
ans = (ans + f[dep[X] - dep[x]][dep[Y] - dep[x]]) % mod;
}
}
for(int y : son[nxt]) son[x].push_back(y);
}
for(int y : son[x]) if(x > y) ans = (ans + 1) % mod;
son[x].push_back(x);
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for(int i = 1, U, V; i < n; i++){
cin >> U >> V, eg[U].push_back(V), eg[V].push_back(U);
}
for(int y = 1; y <= n; y++) f[0][y] = 1;
for(int x = 1; x <= n; x++){
for(int y = 1; y <= n; y++){
f[x][y] = (f[x - 1][y] + f[x][y - 1]) % mod * qpow(2, mod - 2) % mod;
}
}
for(int i = 1; i <= n; i++){
dfs(i, 0);
}
cout << ans * qpow(n, mod - 2) % mod;
return 0;
}
CF436F - Banners
按照 \(a_i\) 的值域建一棵 KTT,每次添加一个元素。
这样的 KTT 复杂度是 \(O((n + m) \log n)\) 的。称左儿子大于右儿子的节点为一个缝隙,则填补一个缝隙的复杂度代价 \(O(\log)\)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e5 + 3, V = 1e5;
const LL inf = 1e15;
struct FC{
LL k, b;
FC operator+ (FC j) const { return {k + j.k, b + j.b}; }
void ADD(LL w){ b += k * w; }
};
pair<FC, LL> MAX(FC a, FC b){
if(a.k < b.k || (a.k == b.k && a.b < b.b)) swap(a, b);
if(a.b >= b.b) return {a, inf};
return {b, (b.b - a.b) / (a.k - b.k)};
}
struct SgTree{
FC mx;
LL x;
SgTree operator+ (SgTree b) const {
SgTree a = {mx, x}, ret;
pair<FC, LL> tmp;
ret.x = min(a.x, b.x);
tmp = MAX(a.mx, b.mx), ret.mx = tmp.first, ret.x = min(ret.x, tmp.second);
return ret;
}
}tr[MAXN * 4];
LL lz[MAXN * 4];
int n, W;
LL ANS = 0, _ANS = 0;
vector<int> Q[MAXN];
void Push(int i, int k){ lz[i] += k, tr[i].x -= k, tr[i].mx.ADD(k); }
void Merge(int i){ tr[i] = tr[i * 2] + tr[i * 2 + 1]; }
void Down(int i){ if(lz[i]) Push(i * 2, lz[i]), Push(i * 2 + 1, lz[i]), lz[i] = 0; }
void Build(int i, int l, int r){
if(l == r){
tr[i] = {{l, 0}, inf};
return;
}
int mid = (l + r) >> 1;
Build(i * 2, l, mid), Build(i * 2 + 1, mid + 1, r), Merge(i);
}
void Force(int i, int l, int r, LL w){
if(w > tr[i].x){
int mid = (l + r) >> 1;
Force(i * 2, l, mid, w + lz[i]), Force(i * 2 + 1, mid + 1, r, w + lz[i]), lz[i] = 0;
Merge(i);
}else Push(i, w);
}
void Update(int i, int l, int r, int L, int R){
if(l == L && r == R){
Force(i, l, r, 1);
return;
}
int mid = (l + r) >> 1;
Down(i);
if(L <= mid) Update(i * 2, l, mid, L, min(mid, R));
if(mid + 1 <= R) Update(i * 2 + 1, mid + 1, r, max(mid + 1, L), R);
Merge(i);
}
int main(){
cin >> n >> W;
int mx = 0;
for(int i = 1, a, b; i <= n; i++){
cin >> a >> b, mx = max(mx, b), Q[b].push_back(a);
}
Build(1, 1, V);
LL sum = 1ll * W * n;
for(int c = 0; c <= mx + 1; c++){
if(c > 0){
for(int x : Q[c - 1]){
if(x > 0) Update(1, 1, V, 1, x);
}
}
cout << sum * c + tr[1].mx.b << " " << tr[1].mx.k << "\n";
sum -= 1ll * W * Q[c].size();
}
return 0;
}
CF804D - Expected diameter of a tree
终于感受到了 CF 题的魅力。
首先这个期望是假的。如何求一个点到其他点的最长路径:换根dp 显然太麻烦,可以先找到直径,然后两个直径端点出发到每个点。(这一定是最长路径)
如果选择 \(x,y\) 则直径为 \(\max(d_S,d_T,mx_x+mx_y+1)\),我们考虑枚举 \(x\),则问题就是找到 \(mx_y \ge \max(d_S,d_T)-mx_x\) 的总和,由于值域是 \(n\) 以内的,可以直接前缀和预处理。
我们考虑枚举较小集合中的 \(x\),然后用 map 记忆化询问。
这样复杂度是 \(O(n\sqrt{n})\) 的。可以分类讨论证明。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 1e5 + 3;
int n, m, Q, k = 0;
vector<int> eg[MAXN], son[MAXN];
int vis[MAXN], d[MAXN], mx[MAXN], sz[MAXN];
vector<LL> sum[2][MAXN];
int getmx = -1, _getmx = 0;
void dfs(int x, int dad, int len){
vis[x] = k, d[k] = max(d[k], len), mx[x] = max(mx[x], len);
if(len > getmx) getmx = len, _getmx = x;
for(int nxt : eg[x]){
if(nxt != dad) dfs(nxt, x, len + 1);
}
}
void init(){
for(int i = 1; i <= n; i++){
if(vis[i]) continue;
PII p;
k++, getmx = -1, dfs(i, 0, 0), p.first = _getmx;
getmx = -1, dfs(p.first, 0, 0), p.second = _getmx;
dfs(p.second, 0, 0);
}
for(int i = 1; i <= n; i++) sz[vis[i]]++, son[vis[i]].push_back(i);
for(int d = 1; d <= k; d++){
for(int i = 0; i <= son[d].size(); i++) sum[0][d].push_back(0), sum[1][d].push_back(0);
for(int x : son[d]){
sum[0][d][mx[x]]++, sum[1][d][mx[x]] += mx[x];
}
for(int i = 1; i <= son[d].size(); i++) sum[0][d][i] += sum[0][d][i-1], sum[1][d][i] += sum[1][d][i-1];
}
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m >> Q;
for(int i = 1, U, V; i <= m; i++){
cin >> U >> V, eg[U].push_back(V), eg[V].push_back(U);
}
init();
map<int, map<int, LL>> mp;
for(int q = 1, x, y; q <= Q; q++){
cin >> x >> y, x = vis[x], y = vis[y];
if(x == y){
cout << -1 << "\n";
continue;
}
if(sz[x] > sz[y]) swap(x, y);
if(mp.find(x) != mp.end() && mp[x].find(y) != mp[x].end()){
cout << fixed <<setprecision(8) << mp[x][y] / double(sz[x]) / double(sz[y]) << "\n";
continue;
}
LL ans = 0, D = max(d[x], d[y]);
for(int i : son[x]){
LL R = D - mx[i]; // 这玩意根本不能小于 0
if(R < sum[1][y].size()){
ans += sum[1][y].back()-(R>0?sum[1][y][R-1]:0) + (sum[0][y].back()-(R>0?sum[0][y][R-1]:0)) * (mx[i] + 1);
ans += (R>0?sum[0][y][R-1]:0) * D;
}else{
ans += 1ll * sz[y] * D;
}
}
cout << fixed <<setprecision(8) << (mp[x][y] = ans) / double(sz[x]) / double(sz[y]) << "\n";
}
return 0;
}
MX - 矩形统计
题面
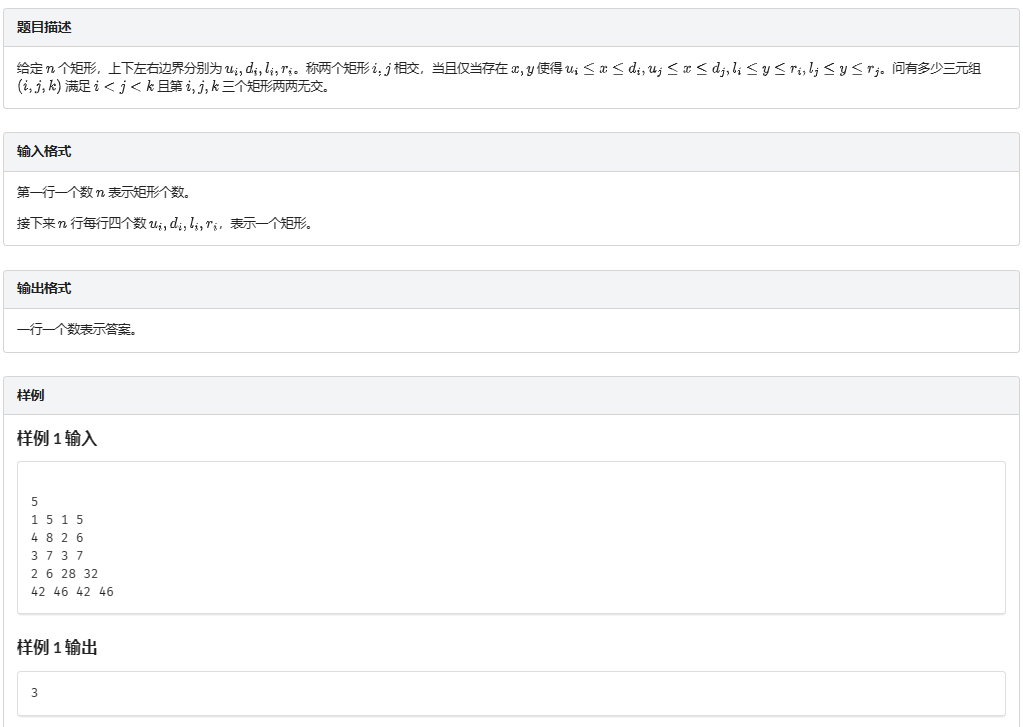
设与一个矩形有交的矩形个数为 \(deg_i\)。考虑容斥,假设我们已经求了三个互相有交的情况,那么只需要算出两个交和一个交的情况,这两种情况的总和为 \(\sum\limits_{i=1}^{n}{\frac{deg_i (n-deg_i-1)}{2}}\)。
std 求 \(deg_i\) 的方法:减去完全在矩形上下左右的矩形个数,然后加上四个角的个数(只需要用到 BIT,不需要线段树)。
求三个互相有交的方法:
- 考虑只在交集的左下角进行统计,再次利用容斥,对于每个 \((x,y)\) 统计 \(\binom{包含 (x,y) 的矩形个数}{3} - \binom{包含 (x,y)(x-1,y) 的矩形个数}{3} - \binom{包含 (x,y)(x,y-1) 的矩形个数}{3} + \binom{包含 (x,y)(x-1,y-1)(x-1,y)(x,y-1) 的矩形个数}{3}\)
- 也就是需要在扫描线的时候维护 \(\sum{\binom{w_i}{3}}\)
- 组合数有 \(\binom{x}{y} = \sum\limits_{j=0}^{y}{\binom{x-p}{j}\binom{p}{y-j}}\)
- 所以线段树区间 \(w\) 加减一的时候可以直接添加。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 4e5 + 3;
struct Square{
int l, r, L, R;
}a[MAXN];
int n, deg[MAXN], visx[MAXN], visy[MAXN];
struct BIT{
int sum[MAXN];
void ADD(int x, int w){
for(; x <= 2 * n; x += (x & (-x))) sum[x] += w;
}
int QUE(int x){
int ret = 0;
for(; x > 0; x -= (x & (-x))) ret += sum[x];
return ret;
}
void Clear(){
for(int x = 0; x <= 2 * n; x++) sum[x] =0 ;
}
}bit1, bit2;
struct SGT{
struct SgTree{
LL a[4];
SgTree operator+ (SgTree j) const {
SgTree ret;
for(int i = 0; i < 4; i++) ret.a[i] = a[i] + j.a[i];
return ret;
}
}tr[MAXN * 4], lz[MAXN * 4];
void Build(int i, int l, int r){
tr[i].a[0] = r - l + 1, lz[i].a[0] = 1;
if(l == r) return;
int mid = (l + r) >> 1;
Build(i * 2, l, mid), Build(i * 2 + 1, mid + 1, r);
}
inline void Push(int i, SgTree w){
for(int j = 3; j >= 0; j--){ // 自然滚动
LL tmp = 0;
for(int h = j; h >= 0; h--) tmp += tr[i].a[h] * w.a[j - h];
tr[i].a[j] = tmp;
}
for(int j = 3; j >= 0; j--){ // 自然滚动
LL tmp = 0;
for(int h = j; h >= 0; h--) tmp += lz[i].a[h] * w.a[j - h];
lz[i].a[j] = tmp;
}
}
inline void Merge(int i){ tr[i] = tr[i * 2] + tr[i * 2 + 1]; };
inline void Down(int i){ Push(i * 2, lz[i]), Push(i * 2 + 1, lz[i]), lz[i] = SgTree{{1, 0, 0, 0}}; }
void Update(int i, int l, int r, int L, int R, int v){
if(l == L && r == R){
Push(i, SgTree{{1, v, v * (v - 1) / 2, v * (v - 1) * (v - 2) / 6}});
return;
}
int mid = (l + r) >> 1;
Down(i);
if(L <= mid) Update(i * 2, l, mid, L, min(mid, R), v);
if(mid + 1 <= R) Update(i * 2 + 1, mid + 1, r, max(mid + 1, L), R, v);
Merge(i);
}
LL Get(){ return tr[1].a[3]; }
}tr1, tr2, tr3, tr4;
LL doit(){ // 求三个相交
LL ret = 0;
tr1.Build(1, 1, 2*n);
tr2.Build(1, 1, 2*n);
tr3.Build(1, 1, 2*n);
tr4.Build(1, 1, 2*n);
for(int i = 1; i <= 2 * n; i++){ int id = abs(visx[i]);
if(visx[i] > 0){
tr1.Update(1, 1, 2*n, a[id].L, a[id].R, 1);
tr2.Update(1, 1, 2*n, a[id].L, a[id].R - 1, 1);
tr3.Update(1, 1, 2*n, a[id].L, a[id].R, 1);
tr4.Update(1, 1, 2*n, a[id].L, a[id].R - 1, 1);
}
if(visx[i] < 0){
tr3.Update(1, 1, 2*n, a[id].L, a[id].R, -1);
tr4.Update(1, 1, 2*n, a[id].L, a[id].R - 1, -1);
}
ret += tr1.Get() - tr2.Get() - tr3.Get() + tr4.Get();
if(visx[i] < 0){
tr1.Update(1, 1, 2*n, a[id].L, a[id].R, -1);
tr2.Update(1, 1, 2*n, a[id].L, a[id].R - 1, -1);
}
}
return ret;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
freopen("rectangle.in", "r", stdin);
freopen("rectangle.out", "w", stdout);
cin >> n;
vector<int> px, py;
for(int i = 1; i <= n; i++){
cin >> a[i].l >> a[i].r >> a[i].L >> a[i].R;
px.push_back(a[i].l), px.push_back(a[i].r), py.push_back(a[i].L), py.push_back(a[i].R);
}
if(n < 3){
cout << 0;
return 0;
}
sort(px.begin(), px.end()), sort(py.begin(), py.end());
for(int i = 1; i <= n; i++){
a[i].l = lower_bound(px.begin(), px.end(), a[i].l) - px.begin() + 1; // 离散化
a[i].r = lower_bound(px.begin(), px.end(), a[i].r) - px.begin() + 1;
a[i].L = lower_bound(py.begin(), py.end(), a[i].L) - py.begin() + 1;
a[i].R = lower_bound(py.begin(), py.end(), a[i].R) - py.begin() + 1;
visx[a[i].l] = i, visx[a[i].r] = -i, visy[a[i].L] = i, visy[a[i].R] = -i;
}
LL sum = 0, ANS = 1ll * n * (n - 1) * (n - 2) / 6;
for(int i = 1; i <= n; i++) deg[i] = n - 1;
for(int i = 1, sum = 0; i <= 2 * n; i++){
if(visx[i] < 0) sum++;
else deg[visx[i]] -= sum;
}
for(int i = 2 * n, sum = 0; i >= 1; i--){
if(visx[i] > 0) sum++;
else deg[-visx[i]] -= sum;
}
for(int i = 1, sum = 0; i <= 2 * n; i++){
if(visy[i] < 0) sum++;
else deg[visy[i]] -= sum;
}
for(int i = 2 * n, sum = 0; i >= 1; i--){
if(visy[i] > 0) sum++;
else deg[-visy[i]] -= sum;
}
bit1.Clear(), bit2.Clear();
for(int i = 1; i <= 2 * n; i++){
if(visx[i] < 0){
bit1.ADD(a[-visx[i]].R, 1), bit2.ADD(2*n - a[-visx[i]].L + 1, 1);
}else{
deg[visx[i]] += bit1.QUE(a[visx[i]].L)+bit2.QUE(2*n - a[visx[i]].R + 1); // 因为保证所有横坐标不同,且所有纵坐标不同,所以这样正确的
}
}
bit1.Clear(), bit2.Clear();
for(int i = 2 * n; i >= 1; i--){
if(visx[i] > 0){
bit1.ADD(a[visx[i]].R, 1), bit2.ADD(2*n - a[visx[i]].L + 1, 1);
}else{
deg[-visx[i]] += bit1.QUE(a[-visx[i]].L)+bit2.QUE(2*n - a[-visx[i]].R + 1);
}
}
ANS -= doit();
LL tmpans = 0;
for(int i = 1; i <= n; i++) tmpans += 1ll * deg[i] * (n - deg[i] - 1);
ANS -= tmpans / 2; // 注意只能在外面除二
cout << ANS;
return 0;
}
[AGC007E] Shik and Travel
参考题解:https://www.luogu.com.cn/article/8ig8oorj
题意:一棵有边权的二叉树,且非叶子有两个儿子。从根节点出发,每次到达一个没到达过的叶子,要求每条边恰好被遍历两次。除第一条路径和最后一条路径,要求最小化其余路径的最大值。
首先二分。题目要求每条边恰好被遍历两次,也就是必须遍历完全一棵子树后才能便利其他子树,似乎可以树形 dp。
有一个暴力的可行性树形 dp。\(f_{x,a,b}\) 表示遍历完全 \(x\) 为根的子树,第一条路径长度 \(a\),最后一条路径长度 \(b\)。如果 \(f_{x,a,b} = 1\) 则所有 \(f_{x,c,d} (c > a 且 d > b)\) 可以忽略,将这种视为不可行状态。
我们只考虑 \(f_{x,a,b} = 1\) 的可行状态,设 \(F_x\) 表示 \(f_{x,a,b}=1\) 可行状态数。感觉 \(\sum{F}\) 很少啊?
有 \(F_x \le 2 \min(F_{ls},F_{rs}) \le F_{ls} + F_{rs}\),所以还有 \(F_x \le sz_x\)。所以 \(F_x \le 2 \min(sz_{ls},sz_{rs})\),标准的启发式合并,而且这个 \(\log n\) 很难跑满,复杂度 \(O(n \log n \log V)\)。
等等,怎么实现?如果按照 \(a\) 小到大排序,则 \(b\) 是从大到小排序,然后就可以双指针。
遍历一个 vector<PLL> vt 用 for(PII w : vt),导致调了 1.5h,在次纪念。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
using PLL = pair<LL, LL>;
const int MAXN = 2e5 + 3;
int n;
PII eg[MAXN][2];
LL D = 0;
vector<PLL> f[MAXN];
void dfs(int x){
if(eg[x][0].first == 0){
f[x].clear(), f[x].push_back({0, 0});
return;
}
f[x].clear();
dfs(eg[x][0].first), dfs(eg[x][1].first);
vector<PLL> vt;
for(int op = 0; op <= 1; op++){
int ls = eg[x][op].first, rs = eg[x][op ^ 1].first;
LL lw = eg[x][op].second, rw = eg[x][op ^ 1].second;
for(int i = 0, j = 0; i < f[ls].size(); i++){
while(j + 1 < f[rs].size() && f[ls][i].second + f[rs][j + 1].first + lw + rw <= D) j++;
if(j < f[rs].size() && f[ls][i].second + f[rs][j].first + lw + rw <= D){
vt.push_back({f[ls][i].first + lw, f[rs][j].second + rw});
}
}
}
sort(vt.begin(), vt.end()); // 这里也可以线性排序两个有序的数组
for(PLL w : vt){ // 这里写挂了一次,调了 1.5h,在次纪念。
if(f[x].empty() || (w.first > f[x].back().first && w.second < f[x].back().second)){
f[x].push_back(w);
}
}
}
bool check(){
for(int i = 1; i <= n; i++) f[i].clear();
dfs(1);
return !f[1].empty();
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for(int i = 1; i <= n; i++) eg[i][0] = eg[i][1] = {0, 0};
for(int i = 2, f, w; i <= n; i++){
cin >> f >> w;
if(eg[f][0].first == 0){
eg[f][0] = {i, w};
}else eg[f][1] = {i, w};
}
LL l = 0, r = 1e15;
while(l < r){
LL mid = (l + r) >> 1;
D = mid;
if(check()){
r = mid;
}else l = mid + 1;
}
D = l;
if(!check()) return 1;
cout << l;
return 0;
}
CF2B - The least round way
一条路径有三种情况:有 \(0\) 存在,\(5\) 的个数更少,\(2\) 的个数更少,分类算即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 1e3 + 3;
int n;
int a[MAXN][MAXN];
PII dp[MAXN][MAXN][2];
int Get(LL w, LL _w){
int cnt = 0;
while(w % _w == 0) w /= _w, cnt++;
return cnt;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
int _op = 0, Sx = 0, Sy = 0;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
cin >> a[i][j];
if(a[i][j] == 0) _op = 1, Sx = i, Sy = j;
}
}
for(int i = 0; i <= n; i++) for(int j = 0; j <= n; j++) dp[i][j][0] = dp[i][j][1] = {1e9, 2};
for(int op = 0; op <= 1; op++){
dp[1][1][op] = {(op == 0 ? Get(a[1][1], 2) : Get(a[1][1], 5)), 0};
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
if(a[i][j] == 0 || (i == 1 && j == 1)) continue;
dp[i][j][op].first = min(dp[i - 1][j][op].first, dp[i][j - 1][op].first) + (op == 0 ? Get(a[i][j], 2) : Get(a[i][j], 5));
if(dp[i - 1][j][op].first < dp[i][j - 1][op].first) dp[i][j][op].second = 1;
else dp[i][j][op].second = 0;
}
}
}
int op = (dp[n][n][0].first < dp[n][n][1].first ? 0 : 1);
if(_op == 0 || dp[n][n][op].first == 0){
string s;
for(int x = n, y = n; x != 1 || y != 1; ){
int d = dp[x][y][op].second;
if(d == 1){
s.push_back('D');
x--;
}else{
s.push_back('R');
y--;
}
}
cout << dp[n][n][op].first << "\n";
reverse(s.begin(), s.end());
cout << s;
}else{
cout << 1 << "\n";
for(int i = 1; i < Sx; i++) cout << "D";
for(int i = 1; i < Sy; i++) cout << "R";
for(int i = 1; i <= n - Sx; i++) cout << "D";
for(int i = 1; i <= n - Sy; i++) cout << "R";
}
return 0;
}
CF316D3 - PE Lesson
\(a\) 表示有多少个 \(1\),\(b\) 表示有多少个 \(2\)。
先考虑 \(b = 0\)。设 \(f_i\) 表示有 \(i\) 个 \(1\) 的方案数。可以得到转移:\(f_i = f_{i - 1} + (i - 1) \cdot f_{i - 2}\)(转移中的 \((i-1)\) 可以看作插入一个数的方案)
考虑 \(b > 0\)。序列总和为 \(a+2*b\),考虑将序列的每个 \(2\) 都减少一,最后序列总和 \(a\),贡献为 \(f_{a}\)。每个 \(2\) 可以选择剩余序列总和中的任意一个,所以方案 \(\prod\limits_{i=1}^{b}{(n-i+1)}\)。
其中的 \((n-i+1)\) 就是 \(a+b-i+1\)。那个 \(+1\) 表示可以自动删除,不产生交换,那个 \(a+b-i\) 表示与其他删除但不与自己删除。
最后答案为 \(f_a \prod\limits_{i=1}^{b}{(n-i+1)}\)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const LL mod = 1e9 + 7;
const int MAXN = 1e6 + 3;
int n, a = 0, b = 0;
LL f[MAXN];
int main(){
cin >> n;
for(int i = 1, x; i <= n; i++){
cin >> x;
if(x == 1) a++;
else b++;
}
f[1] = 1, f[0] = 1;
for(int i = 2; i <= a; i++){
f[i] = f[i - 1] + f[i - 2] * (i - 1) % mod;
f[i] %= mod;
}
LL ans = f[a];
for(int i = 1; i <= b; i++){
ans = ans * (n - i + 1) % mod;
}
cout << ans;
return 0;
}
CF257D - Sum
小清新构造题。感觉从前往后有些困难,试着从后往前。
设当前后缀和 \(s\),如果能减就建,不能减就加。根据限制 \(a_i \le a_{i + 1} \le 2 * a_i\),这个 \(s\) 一定是时刻保持小于等于 \(a_i\) 的。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e5 + 3;
int n, a[MAXN];
int main(){
string s;
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
LL sum = 0;
for(int i = n; i >= 1; i--){
if(abs(sum - a[i]) <= a[i]){
sum -= a[i], s.push_back('-');
}else{
sum += a[i], s.push_back('+');
}
}
reverse(s.begin(), s.end());
if(sum < 0){
for(int i = 0; i < n; i++) s[i] = (s[i] == '-' ? '+' : '-');
}
cout << s;
return 0;
}
[ARC143E] Reversi
突破口在于考虑叶子节点。
如果叶子为白,则必须先删除叶子,否则必须先删除父亲。
先 dfs 建立限制关系,然后跑拓扑排序。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 2e5 + 3;
int n;
vector<int> eg[MAXN], r[MAXN];
int a[MAXN], d[MAXN];
void dfs(int x, int dad){
for(int nxt : eg[x]){
if(nxt == dad) continue;
dfs(nxt, x);
a[x] ^= a[nxt];
if(a[nxt] == 1){
r[nxt].push_back(x), d[x]++;
}else{
r[x].push_back(nxt), d[nxt]++;
}
}
}
int main(){
cin >> n;
for(int i = 1, U, V; i < n; i++){
cin >> U >> V, eg[U].push_back(V), eg[V].push_back(U);
}
for(int i = 1; i <= n; i++){
char ch; cin >> ch;
a[i] = ch == 'W' ? 1 : 0;
}
dfs(1, 0);
if(!a[1]){
cout << -1;
return 0;
}
priority_queue<int, vector<int>, greater<int>> pq;
vector<int> ans;
for(int i = 1; i <= n; i++) if(!d[i]) pq.push(i);
while(!pq.empty()){
int i = pq.top();
pq.pop(), ans.push_back(i);
for(int nxt : r[i]){
d[nxt]--;
if(!d[nxt]) pq.push(nxt);
}
}
if(ans.size() != n){
cout << -1;
return 0;
}
for(int x : ans) cout << x << " ";
return 0;
}
CF2018D - Max Plus Min Plus Size
突破口:选择最大值一定是不劣的。因为如果可以通过删除两个元素添加一个更大的元素,答案显然不会劣。
然后就是简单的并查集维护了。然后需要判断是否存在一个子段的最优子序列包含了至少一个最大值,若不是则答案减一。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 2e5 + 3;
int n, a[MAXN], p[MAXN];
int fa[MAXN], sz[MAXN], w[MAXN], l[MAXN], r[MAXN];
int ans = 0, op = 1;
set<int> st[2];
int Getf(int x){ return fa[x] == x ? x : fa[x] = Getf(fa[x]); }
int I(int x){ return (x + 1) / 2; }
void Merge(int x, int y){
int fx = Getf(x), fy = Getf(y);
ans -= I(sz[fx]), ans -= I(sz[fy]), op -= w[fx] + w[fy];
sz[fy] += sz[fx], l[fy] = min(l[fy], l[fx]), r[fy] = max(r[fy], r[fx]), fa[fx] = fy;
ans += I(sz[fy]);
int L = l[fy], o = L & 1;
auto it = st[o].lower_bound(L), _it = st[o^1].lower_bound(L);
w[fy] = (sz[fy] % 2 == 0 && ((it != st[o].end() && *it <= r[fy]) || (_it != st[o^1].end() && *_it <= r[fy])))
|| (it != st[o].end() && *it <= r[fy]);
op += w[fy];
}
void Insert(int p, int o){
fa[p] = p, sz[p] = 1, ans += I(sz[p]), l[p] = r[p] = p;
if(o) w[p] = 1, op++;
if(p > 1 && fa[p - 1] > 0) Merge(p, p - 1);
if(p < n && fa[p + 1] > 0) Merge(p, p + 1);
}
void work(){
cin >> n;
ans = 0, op = 0;
for(int i = 0; i <= n + 1; i++) fa[i] = 0, sz[i] = 0, w[i] = 0;
for(int i = 1; i <= n; i++){
cin >> a[i], p[i] = i;
}
sort(p + 1, p + 1 + n, [](int i, int j){ return a[i] > a[j]; });
st[0].clear(), st[1].clear();
for(int i = 1; i <= n; i++){
if(a[p[i]] != a[p[1]]) break;
st[p[i]&1].insert(p[i]);
}
int j = 1, ANS = 0;
while(j <= n && a[p[1]] == a[p[j]]) Insert(p[j], 1), j++;
ANS = max(ANS, ans + a[p[1]] + a[p[1]] - (!op));
while(j <= n){
int w = a[p[j]];
while(j <= n && w == a[p[j]]) Insert(p[j], 0), j++;
ANS = max(ANS, ans + w + a[p[1]] - (!op));
}
cout << ANS << "\n";
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
int T;
cin >> T;
while(T--){
work();
}
return 0;
}
CF1870E - Another MEX Problem
\(mex\) 的复杂度优化性质实在太多了,这就是其中之一。
内部不存在子段 \(mex\) 等于自身 \(mex\) 的区间,称之为好区间。感觉这样的区间个数不多。
好一定满足 \(a_l,a_r < mex\)。
- \(a_l > a_r\),设存在 \(R > r\) 且 \(a_l > a_R\)
- 有 \(a_R < a_l < mex\),说明 \(a_R\) 在区间 \([l,r]\) 已经出现过了,\(R\) 可以被抛弃,\([l,R]\) 不是好区间。
- \(a_l < a_r\),同理
所以好区间个数最多 \(2n\) 个,注意需要特殊处理 \(0\)。拿出来转移即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 5000 + 3;
int n, a[MAXN], b[MAXN];
bitset<MAXN * 2> dp[MAXN];
vector<PII> q[MAXN];
void work(){
cin >> n;
for(int i = 1; i <= n; i++){
cin >> a[i], q[i].clear();
}
for(int i = 1; i <= n; i++){
if(!a[i]) q[i].push_back({i, 1});
}
for(int i = 1; i <= n; i++){
for(int k = 0; k <= n; k++) b[k] = 0;
int mex = 0;
for(int j = i; j <= n; j++){
b[a[j]] = 1;
while(b[mex]) mex++;
if(mex > a[i] && a[i] > a[j]){
q[j].push_back({i, mex}); break;
}
}
}
for(int i = 1; i <= n; i++){
for(int k = 0; k <= n; k++) b[k] = 0;
int mex = 0;
for(int j = i; j >= 1; j--){
b[a[j]] = 1;
while(b[mex]) mex++;
if(mex > a[i] && a[i] > a[j]){
q[i].push_back({j, mex}); break;
}
}
}
dp[0].reset(), dp[0].flip(0);
for(int i = 1; i <= n; i++){
dp[i] = dp[i - 1];
for(PII Q : q[i]){ int j = Q.first;
for(int k = 0; k <= n * 2; k++){
int _k = k ^ Q.second;
if(_k > 2 * n) continue;
if(dp[j - 1][_k]) dp[i].set(k);
}
}
}
for(int k = n * 2; k >= 0; k--){
if(dp[n][k]){
cout << k << "\n";
return;
}
}
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
int T; cin >> T;
while(T--) work();
return 0;
}
luogu - P3588 [POI2015] PUS
可以建限制,\(a_i\) 一定是越大越好,拓扑排序(注意需要队列实现)。但即便线段树建图也需要 \(k^2\),我们考虑一个东西:集中点。
对于 \(k\) 給点设一个集中点,然后就是每个区间先集中点连边了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
using PLI = pair<LL, int>;
const int MAXN = 5e5 + 3;
struct SgTree{
int ls, rs;
}tr[MAXN * 4];
int tot = 0, root = 0;
int n, s, Q, pos[MAXN], vis[MAXN], b[MAXN], a[MAXN * 4], d[MAXN * 4], mx[MAXN * 4];
vector<int> eg[MAXN * 4];
void Build(int &i, int l, int r){ // 入树
i = ++tot;
if(l == r){
pos[l] = i, vis[i] = l;
return;
}
int mid = (l + r) >> 1;
Build(tr[i].ls, l, mid), Build(tr[i].rs, mid + 1, r);
eg[i].push_back(tr[i].ls), eg[i].push_back(tr[i].rs), d[tr[i].ls]++, d[tr[i].rs]++;
}
void ADD(int i, int l, int r, int L, int R, int v){
if(l == L && r == R){
eg[v].push_back(i), d[i]++;
return;
}
int mid = (l + r) >> 1;
if(L <= mid) ADD(tr[i].ls, l, mid, L, min(mid, R), v);
if(mid + 1 <= R) ADD(tr[i].rs, mid + 1, r, max(mid + 1, L), R, v);
}
void No(){
cout << "NIE";
exit(0);
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> s >> Q;
Build(root, 1, n);
for(int i = 1, p, d; i <= s; i++){
cin >> p >> d, a[pos[p]] = d;
}
int _tot = tot;
for(int q = 1, r, k; q <= Q; q++){
cin >> b[0] >> r >> k, b[0]--, tot++;
for(int i = 1; i <= k; i++){
cin >> b[i], eg[pos[b[i]]].push_back(tot), d[tot]++;
if(b[i] != b[i - 1] + 1) ADD(1, 1, n, b[i - 1] + 1, b[i] - 1, tot);
}
if(b[k] != r) ADD(1, 1, n, b[k] + 1, r, tot);
}
queue<int> que;
for(int i = 1; i <= tot; i++){
if(!d[i]) que.push(i);
mx[i] = 1e9;
}
int cnt = 0;
while(!que.empty()){
int i = que.front();
que.pop(), cnt++;
if(i > _tot) mx[i]--;
if(mx[i] < 1) No();
if(a[i]){
if(mx[i] < a[i]) No();
mx[i] = a[i];
}
for(int nxt : eg[i]){
d[nxt]--, mx[nxt] = min(mx[nxt], mx[i]);
if(!d[nxt]) que.push(nxt);
}
}
if(cnt != tot) No();
cout << "TAK\n";
for(int i = 1; i <= n; i++) cout << mx[pos[i]] << " ";
return 0;
}
luogu - P9871 [NOIP2023] 天天爱打卡
参考题解:https://www.luogu.com.cn/article/h5hw8b39
首先得到 \(O(n \log n)\) 的线段树优化 dp 的做法,然后发现重要的只有 \(l-1\) 和 \(r\),离散化即可。
好傻逼的题啊,还卡 map 离散化。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 2e5 + 3;
const LL inf = 1e18;
struct Ask{
int l, r, v;
}a[MAXN];
int n, k, m, s = 0, d, ls[MAXN];
LL dp[MAXN];
LL lz[MAXN * 4], tr[MAXN * 4]; // 线段树
inline void Merge(int i){ tr[i] = max(tr[i * 2], tr[i * 2 + 1]); }
inline void Push(int i, LL w){ tr[i] += w, lz[i] += w; }
inline void Down(int i){ Push(i * 2, lz[i]), Push(i * 2 + 1, lz[i]), lz[i] = 0; }
void Build(int i, int l, int r){
lz[i] = 0, tr[i] = 0;
if(l == r){
tr[i] = (l == 1 ? 0 : -inf);
return;
}
int mid = (l + r) >> 1;
Build(i * 2, l, mid), Build(i * 2 + 1, mid + 1, r);
Merge(i);
}
int opt = 0;
LL ww;
void Update(int i, int l, int r, int L, int R){
if(l == L && r == R){
if(opt == 0){
tr[i] = ww;
}else{
Push(i, ww);
}
return;
}
int mid = (l + r) >> 1;
Down(i);
if(L <= mid) Update(i * 2, l, mid, L, min(mid, R));
if(mid + 1 <= R) Update(i * 2 + 1, mid + 1, r, max(mid + 1, L), R);
Merge(i);
}
LL Query(int i, int l, int r, int L, int R){
if(l == L && r == R){
return tr[i];
}
int mid = (l + r) >> 1;
LL ret = -inf;
Down(i);
if(L <= mid) ret = max(ret, Query(i * 2, l, mid, L, min(mid, R)));
if(mid + 1 <= R) ret = max(ret, Query(i * 2 + 1, mid + 1, r, max(mid + 1, L), R));
return ret;
}
void init(){ // 读入 + 离散化
cin >> n >> m >> k >> d;
s = 0;
vector<int> p;
p.push_back(-1);
for(int i = 1; i <= m; i++){
cin >> a[i].r >> a[i].l >> a[i].v, a[i].l = a[i].r - a[i].l; // l--
p.push_back(a[i].l), p.push_back(a[i].r);
}
sort(p.begin(), p.end());
s = unique(p.begin(), p.end()) - p.begin();
while(p.size() > s) p.pop_back();
for(int i = 0; i < s; i++) ls[i + 1] = p[i];
for(int i = 1; i <= m; i++){
a[i].l = lower_bound(p.begin(), p.end(), a[i].l) - p.begin() + 1;
a[i].r = lower_bound(p.begin(), p.end(), a[i].r) - p.begin() + 1;
}
}
void work(){
init();
sort(a + 1, a + 1 + m, [](Ask i, Ask j){ return i.r < j.r; });
Build(1, 1, s);
LL mx = 0;
for(int t = 2, j = 1, lt = 1; t <= s; t++){
ww = mx + 1ll * d * ls[t], opt = 0, Update(1, 1, s, t, t);
while(j <= m && a[j].r == t){
ww = a[j].v, opt = 1, Update(1, 1, s, 1, a[j].l), j++;
}
while(lt < t && k < ls[t] - ls[lt]) lt++;
if(lt < t){
dp[t] = Query(1, 1, s, lt, t - 1) - 1ll * d * ls[t];
}else dp[t] = -inf;
mx = max(mx, dp[t]);
}
cout << mx << "\n";
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
//freopen("run2.in", "r", stdin);
int uid, T; cin >> uid >> T;
while(T--) work();
return 0;
}
luogu - P7214 [JOISC2020] 治療計画
以时间为横坐标,村名编号为纵坐标,从二维平面思考可能更容易想到。
如果两次治疗可以汇合(即相交或相连之前都还没有耗尽),就需要满足 \(|T_i - T_j| \le r_i - l_j\) 或 \(|T_i - T_j| \le l_i - r_j\)。
我们做一个 \(1\) 到 \(n\) 的 dp 转移,每次先右跳,这个过程可以用最短路优化,两点满足 \(|T_i - T_j| \le r_j - l_i\) 就可以由 \(j\) 转移到 \(i\)。
你可能会说如果 \(r_i < l_j\) 怎么办?这种转移是多余的,转移了也没有用处。
但是暴力建边会超时。然后就是类似 P5471 [NOI2019] 弹跳 的做法。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
using PLI = pair<LL, int>;
const int MAXN = 1e5 + 3;
const LL inf = 1e15;
struct Node{
int t, l, r, c;
}a[MAXN];
int N, n, vis[MAXN];
LL dp[MAXN];
priority_queue<PLI> pq;
set<PII> st[2][MAXN * 4];
void Insert(int o, int i, int l, int r, int p, PLI w){
st[o][i].insert(w);
if(l == r) return;
int mid = (l + r) >> 1;
if(p <= mid) Insert(o, i * 2, l, mid, p, w);
else Insert(o, i * 2 + 1, mid + 1, r, p, w);
}
// |Ti - Tj| <= Rj - Li + 1
// Ti - Tj <= Rj - Li + 1
// Ti + Li <= Rj + Tj + 1
// Tj - Ti <= Rj - Li + 1
// Li - Ti <= Rj - Tj + 1
void Update(int o, int i, int l, int r, int L, int R, LL w, LL W){
if(l == L && r == R){
while(!st[o][i].empty() && st[o][i].begin()->first <= w){
PLI s = *st[o][i].begin();
st[o][i].erase(st[o][i].begin());
if(dp[s.second] < inf) continue;
dp[s.second] = W + a[s.second].c, pq.push({-dp[s.second], s.second});
}
return;
}
int mid = (l + r) >> 1;
if(L <= mid) Update(o, i * 2, l, mid, L, min(mid, R), w, W);
if(mid + 1 <= R) Update(o, i * 2 + 1, mid + 1, r, max(mid + 1, L), R, w, W);
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> N >> n;
for(int i = 1; i <= n; i++){
cin >> a[i].t >> a[i].l >> a[i].r >> a[i].c;
}
sort(a + 1, a + 1 + n, [](Node i, Node j){ return i.t < j.t; });
for(int i = 1; i <= n; i++){
if(a[i].l == 1){
pq.push({-a[i].c, i}), dp[i] = a[i].c;
}else{
dp[i] = inf;
Insert(0, 1, 1, n, i, PLI({a[i].l - a[i].t, i})), Insert(1, 1, 1, n, i, PLI({a[i].l + a[i].t, i}));
}
}
while(!pq.empty()){
int i = pq.top().second;
pq.pop();
if(vis[i]) continue;
vis[i] = 1;
if(i > 1) Update(0, 1, 1, n, 1, i - 1, a[i].r - a[i].t + 1, dp[i]);
if(i < n) Update(1, 1, 1, n, i + 1, n, a[i].r + a[i].t + 1, dp[i]);
}
LL ans = inf;
for(int i = 1; i <= n; i++){
if(a[i].r == N) ans = min(ans, dp[i]);
}
cout << (ans >= inf ? -1 : ans);
return 0;
}
luogu - P5470 [NOI2019] 序列
考虑如何反悔贪心。
先选择 \(a,b\) 中前 \(k\) 大的,考虑每次操作增加交集大小。大力分讨。
接下来都是选择 \(i,j\) 满足 \(i\) 只选了 \(a\),\(j\) 只选了 \(b\)。
- 抛弃 \(a_i\),选择 \(a_j\)
- 抛弃 \(b_j\),选择 \(b_i\)
- 抛弃 \(a_i,b_j\),选择目前两个都没选的 \(h\),选择 \(a_h,b_h\)
- 选择目前两个都没选的 \(h\),抛弃 \(a_h,b_h\),选择 \(a_j,b_i\)
至于这些操作为什么会满足反悔,具体证明不会。
6 个 堆维护 \(a_i,b_i,a_i+b_i\) 的最大值最小值。也就是维护 \(a_i,-a_i,b_i,-b_i,a_i+b_i,-a_i-b_i\)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PLI = pair<LL, int>;
const int MAXN = 2e5 + 3;
int n, k, L, p[MAXN], a[MAXN], b[MAXN];
int op[MAXN];
priority_queue<PLI> pq1, pq2, pq3, pq4, pq5, pq6;
void work(){
while(!pq1.empty()) pq1.pop();
while(!pq2.empty()) pq2.pop();
while(!pq3.empty()) pq3.pop();
while(!pq4.empty()) pq4.pop();
while(!pq5.empty()) pq5.pop();
while(!pq6.empty()) pq6.pop();
for(int i = 1; i <= n; i++) op[i] = 0;
LL ANS = 0;
cin >> n >> k >> L;
for(int i = 1; i <= n; i++){
cin >> a[i], p[i] = i;
}
sort(p + 1, p + 1 + n, [](int i, int j){ return a[i] > a[j]; });
for(int i = 1; i <= k; i++) op[p[i]]++, ANS += a[p[i]];
for(int i = 1; i <= n; i++){
cin >> b[i], p[i] = i;
}
sort(p + 1, p + 1 + n, [](int i, int j){ return b[i] > b[j]; });
for(int i = 1; i <= k; i++) op[p[i]] += 2, ANS += b[p[i]];
for(int i = 1; i <= n; i++){
pq1.push({a[i], i}), pq2.push({- a[i], i});
pq3.push({b[i], i}), pq4.push({- b[i], i});
pq5.push({a[i]+b[i], i}), pq6.push({- a[i] - b[i], i}), L -= (op[i] == 3);
}
while(L > 0){
L--;
while(!pq3.empty() && op[pq3.top().second] != 1) pq3.pop();
while(!pq4.empty() && op[pq4.top().second] != 2) pq4.pop();
LL now = -1e18;
int opt = 0, i, j, h;
if(!pq3.empty() && !pq4.empty()){ // first
LL w = b[pq3.top().second] - b[pq4.top().second];
if(w > now) now = w, opt = 1, i = pq3.top().second, j = pq4.top().second;
}
while(!pq1.empty() && op[pq1.top().second] != 2) pq1.pop();
while(!pq2.empty() && op[pq2.top().second] != 1) pq2.pop();
if(!pq1.empty() && !pq2.empty()){ // second
LL w = a[pq1.top().second] - a[pq2.top().second];
if(w > now) now = w, opt = 2, i = pq1.top().second, j = pq2.top().second;
}
while(!pq5.empty() && op[pq5.top().second] != 0) pq5.pop();
if(!pq4.empty() && !pq2.empty() && !pq5.empty()){ // third
LL w = a[pq5.top().second]+b[pq5.top().second] - a[pq2.top().second] - b[pq4.top().second];
if(w > now) now = w, opt = 3, i = pq2.top().second, j = pq4.top().second, h = pq5.top().second;
}
while(!pq6.empty() && op[pq6.top().second] != 3) pq6.pop();
if(!pq1.empty() && !pq3.empty() && !pq6.empty()){ // fourth
LL w = a[pq1.top().second] + b[pq3.top().second] - a[pq6.top().second] - b[pq6.top().second];
if(w > now) now = w, opt = 4, i = pq1.top().second, j = pq3.top().second, h = pq6.top().second;
}
// finish
ANS += now;
if(opt == 1){
pq3.pop(), pq4.pop();
op[j] = 0, op[i] = 3;
pq5.push({a[j] + b[j], j});
pq6.push({- a[i] - b[i], i});
}else if(opt == 2){
pq1.pop(), pq2.pop();
op[j] = 0, op[i] = 3;
pq5.push({a[j] + b[j], j});
pq6.push({- a[i] - b[i], i});
}else if(opt == 3){
pq2.pop(), pq4.pop(), pq5.pop();
op[h] = 3, op[i] = 0, op[j] = 0;
pq5.push({a[i] + b[i], i});
pq5.push({a[j] + b[j], j});
pq6.push({- a[h] - b[h], h});
}else{
pq1.pop(), pq3.pop(), pq6.pop();
op[i] = 3, op[j] = 3, op[h] = 0;
pq6.push({- a[i] - b[i], i});
pq6.push({- a[j] - b[j], j});
pq5.push({a[h] + b[h], h});
}
}
cout << ANS << "\n";
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
int T;
cin >> T;
while(T--) work();
return 0;
}
CF436E - Cardboard Box
考慮如何反悔贪心。
有四种操作:
- 删除 \(a_i\),选择 \(b_i\)
- 选择 \(a_i\)
- 删除 \(a_i\),选择 \(b_j\)
- 删除 \(b_i\),选择 \(a_i\),选择 \(b_j\)
五个堆维护 \(a_i,-b_i,-a_i,b_i-a_i,a_i-b_i\)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PLI = pair<LL, int>;
const int MAXN = 3e5 + 3;
int n, S, a[MAXN], b[MAXN];
int op[MAXN];
priority_queue<PLI> pq1, pq2, pq3, pq4, pq5;
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> S;
for(int i = 1; i <= n; i++){
cin >> a[i] >> b[i], op[i] = 0;
pq1.push({a[i], i}), pq2.push({-b[i], i}), pq3.push({-a[i], i});
pq4.push({b[i]-a[i], i}), pq5.push({a[i]-b[i], i});
}
LL ANS = 0;
while(S--){
LL now = 1e18;
int opt = 0, i = 0, j = 0;
while(!pq5.empty() && op[pq5.top().second] != 1) pq5.pop();
if(!pq5.empty()){
LL w = b[pq5.top().second] - a[pq5.top().second];
if(w < now) now = w, opt = 1, i = pq5.top().second;
}
while(!pq3.empty() && op[pq3.top().second] != 0) pq3.pop();
if(!pq3.empty()){
LL w = a[pq3.top().second];
if(w < now) now = w, opt = 2, i = pq3.top().second;
}
while(!pq1.empty() && op[pq1.top().second] != 1) pq1.pop();
while(!pq2.empty() && op[pq2.top().second] != 0) pq2.pop();
if(!pq1.empty() && !pq2.empty()){
LL w = b[pq2.top().second] - a[pq1.top().second];
if(w < now) now = w, opt = 3, i = pq1.top().second, j = pq2.top().second;
}
while(!pq4.empty() && op[pq4.top().second] != 2) pq4.pop();
if(!pq4.empty() && !pq2.empty()){
LL w = a[pq4.top().second] - b[pq4.top().second] + b[pq2.top().second];
if(w < now) now = w, opt = 4, i = pq4.top().second, j = pq2.top().second;
}
if(opt == 1){
pq5.pop();
op[i] = 2;
pq4.push({b[i]-a[i], i});
}else if(opt == 2){
pq3.pop();
op[i] = 1;
pq5.push({a[i]-b[i], i});
pq1.push({a[i], i});
}else if(opt == 3){
pq1.pop(), pq2.pop();
op[j] = 2, op[i] = 0;
pq4.push({b[j]-a[j], j});
pq3.push({-a[i], i});
pq2.push({-b[i], i});
}else if(opt == 4){
pq4.pop(), pq2.pop();
op[i] = 1, op[j] = 2;
pq4.push({b[j]-a[j], j});
pq5.push({a[i]-b[i], i});
pq1.push({a[i], i});
}
ANS += now;
}
cout << ANS << "\n";
for(int i = 1; i <= n; i++) cout << op[i];
return 0;
}
luogu - P5308 [COCI2018-2019#4] Akvizna
正着 dp 很难做,我们就逆着做 dp,容易得到转移式子,wqs二分 + 斜率优化 做即可。这题的凸性很难看出来,建议直接猜。
对于精度要求很高的实数二分,可以用代码中的写法。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using LD = long double;
const int MAXN = 1e5 + 3;
int n, m, cnt[MAXN];
LD mid, f[MAXN];
int hi = 1, t = 0, dq[MAXN];
LD Slope(int i, int j){
return LD(f[i] - f[j]) / LD(i - j);
}
bool check(){
hi = 1, t = 0, dq[++t] = 0;
for(int i = 1; i <= n; i++){
while(hi < t && Slope(dq[hi], dq[hi + 1]) >= 1.0 / LD(i)) hi++;
f[i] = f[dq[hi]] - 1.0 / LD(i) * dq[hi] + 1 - mid;
cnt[i] = cnt[dq[hi]] + 1;
while(hi < t && Slope(dq[t - 1], dq[t]) <= Slope(dq[t], i)) t--;
dq[++t] = i;
}
return cnt[n] >= m;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
long double l = 0, r = 1e6;
for(int d = 0; d < 200; d++){ // 如果精度要求很高就可以用这种实数二分
mid = (l + r) / 2.0;
if(check()){
l = mid;
}else r = mid;
}
mid = l, check();
cout << fixed << setprecision(9) << f[n] + mid * m;
return 0;
}
/*
f[i] = f[j] + (i - j) / i - D
f[i] - 1 + D = f[j] - j / i
b = f[i] - 1 + D
y = f[j], x = j
k = 1 / i
*/
luogu - P4127 [AHOI2009] 同类分布
数位 dp。
不允许歧视记忆化搜索!!!
这题的记忆化搜索非常好些,但是 dp 就有些难写了(要写很多个循环)。
\(f(p,d,s,ms)\) 表示当前是否可以随意选,当前在确定第 \(d\) 位,当前位数和为 \(s\),当前取模意义下的和为 \(ms\)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int m = 0, c[20], mod;
LL po[20], f[2][20][200][200];
LL Solve(int p, int d, int s, int ms){
if(s < 0) return 0;
if(d == 0) return p && !s && !ms;
if(f[p][d][s][ms] != -1) return f[p][d][s][ms];
LL ret = 0;
for(int i = 0, r = (p ? 9 : c[d]); i <= r; i++){
ret += Solve(p | (i < c[d]), d - 1, s - i, (ms + po[d-1] % mod * i % mod) % mod);
}
return f[p][d][s][ms] = ret;
}
LL work(LL n){
m = 0;
while(n > 0) c[++m] = n % 10, n /= 10;
LL ret = 0;
for(mod = 1; mod <= m * 9; mod++){
memset(f, -1, sizeof(f));
ret += Solve(0, m, mod, 0);
}
return ret;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
po[0] = 1;
for(int i = 1; i <= 17; i++) po[i] = po[i - 1] * 10;
LL a, b;
cin >> a >> b;
cout << work(b + 1) - work(a);
return 0;
}
luogu - P1350 车的放置
当你在思考算组合数的时候,你已经输了......
如果从左向右 dp 行不通,就从右向左 dp,转移和状态设计是简单的。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const LL mod = 1e5 + 3;
const int MAXN = 2e3 + 3;
int a, b, c, d, k, h[MAXN];
LL f[MAXN][MAXN];
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> a >> b >> c >> d >> k;
for(int i = 1; i <= a; i++) h[i] = b + d;
for(int i = a + 1; i <= a + c; i++) h[i] = d;
f[a + c + 1][0] = 1;
for(int i = a + c; i >= 1; i--){
f[i][0] = f[i + 1][0];
for(int j = 1; j <= k; j++){
f[i][j] = (f[i + 1][j] + f[i + 1][j - 1] * (h[i] - j + 1) % mod) % mod;
}
}
cout << f[1][k];
return 0;
}
P5947 [POI2003] Trinomial
初中数学题......
\((x^2+x+1)^n = ((x-1)^3 + 3x)^n\),由于对三取模,变为求 \((x - 1)^{2n}\)。
利用二项式定理,得到第 \(i\) 次的系数为 \((-1)^i C_{2n}^{i}\),然后用一下 Lucas 定理就解决了。
有些久没用 Lucas 了,注意如果 \(n \bmod p > m \bmod p\),则 \(C\) 就是 \(0\),不能不算。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int fac(int w){ return (w == 0 || w == 1 ? 1 : 2); }
int ifac(int w){ return (w == 0 || w == 1 ? 1 : 2); }
LL C(LL A, LL B){
LL ret = 1;
while(A > 0 && B > 0){
int a = A % 3, b = B % 3;
if(a <= b){
ret = ret * fac(a) * fac(b - a) * ifac(b) % 3;
}else ret = 0;
A /= 3, B /= 3;
}
return ret;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
int T;
cin >> T;
while(T--){
LL n, i;
cin >> n >> i;
LL ans = C(i, 2 * n);
cout << (i & 1 ? (3 - ans) % 3 : ans) << "\n";
}
return 0;
}
luogu - P1463 [POI2001] [HAOI2007] 反素数
考虑暴力搜,怎么搜索?也就是找到约数个数最多,其次满足值最小(因为题目要求的是 \(>\))。
直接搜可能难以通过,有什么多余的吗?设质因数分解 \(p_i\) 递增,对于 \(i < j\),如果 \(k_i < k_j\),交换 \(i,j\) 一定更优秀
得到结论:\(k_i\) 随 \(p_i\) 递增,而递减。然后搜索就非常快了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int prime[30] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};
int n;
LL ans1 = 0, ans2 = 0;
void dfs(int x, LL s, LL _s, int pr){
if(s > n) return;
if(!pr){
if(_s > ans1){
ans1 = _s, ans2 = s;
}else if(_s == ans1) ans2 = min(ans2, s);
return;
}
LL po = 1;
for(int k = 0; k <= pr; k++){
if(s * po > n) return;
dfs(x + 1, s * po, _s * (k + 1), k);
po *= prime[x];
}
}
int main(){
cin >> n;
dfs(1, 1, 1, 100);
cout << ans2;
return 0;
}
wildwolf - 20241002模拟测T2
题面
一个序列,从 $1$ 开始反复跳(一次向右,一次向左,交替),答案加上子段和,要求每次跳之后答案非负,总共跳 $k$ 次。最大化最终答案。\(1 \le n \le 1000\) 且 \(0 \le |a_i| \le 10^5\) 且 \(0 \le k \le 10^8\)
初步思路容易想到多次跳跃找到全局最大子段和,然后反复跳跃。
可以得到:一定是首先花最少次数,其次得到最多答案。
然后最短路即可。
luogu - P9521 [JOISC2022] 京都观光
超級抽象的贪心题!!!
简易题面:https://www.luogu.com.cn/problem/AT_joisc2022_b
参考题解:https://blog.csdn.net/cqbzlydd/article/details/130562472 & https://www.luogu.com.cn/article/ycf2xhx6
考虑三种走法:设 \(x<y<z\) 和 \(l<r\)
- \((x,l)\) 到 \((z,l)\) 再到 \((z,r)\)
- \((x,l)\) 到 \((x,r)\) 再到 \((z,r)\)
- \((x,l)\) 到 \((y,l)\) 再到 \((y,r)\) 再到 \((z,r)\)
列出每一种走法的代价,一三比较 + 二三比较,可以得到不等式:\(\frac{a_y - a_x}{y - x} < \frac{b_r - b_l}{r - l} < \frac{a_z - a_y}{z - y}\)
所以只有 \(\frac{a_y - a_x}{y - x} < \frac{a_z - a_y}{z - y}\) 才可能用到第三种走法。对于 \(b\) 也是一样的推导。
由于任意最优路径中间的三个 \(x,y,z\) 都是第三种走法,上面的结论即:最优路径中斜率递增。
贪心地,我们只维护下凸壳,因为每个凸壳内部的点都可以被替代且更优。
只用维护 \(a,b\) 的下凸壳,具体每次是走第一种还是第二种,就需要再推一下式子(直接列出来,然后不等式不断移项),得到:如果 \(\frac{b_r - b_l}{r - l} < \frac{a_z - a_x}{z - x}\) 就第二种。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using ULL = unsigned long long;
using PII = pair<int, int>;
const int MAXN = 1e5 + 3;
int n, m;
int a[MAXN], b[MAXN];
int ha = 1, ta = 0, dqa[MAXN];
int hb = 1, tb = 0, dqb[MAXN];
bool check_a(int x, int y, int z){
return LL(a[y] - a[x]) * (z - y) < LL(a[z] - a[y]) * (y - x);
}
bool check_b(int x, int y, int z){
return LL(b[y] - b[x]) * (z - y) < LL(b[z] - b[y]) * (y - x);
}
bool check_ab(int i, int j, int x, int y){
return LL(a[j] - a[i]) * (y - x) >= LL(b[y] - b[x]) * (j - i);
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; i++){
cin >> a[i];
}
for(int i = 1; i <= m; i++){
cin >> b[i];
}
for(int i = 1; i <= n; i++){
while(ha < ta && !check_a(dqa[ta - 1], dqa[ta], i)) ta--;
dqa[++ta] = i;
}
for(int i = 1; i <= m; i++){
while(hb < tb && !check_b(dqb[tb - 1], dqb[tb], i)) tb--;
dqb[++tb] = i;
}
LL ans = 0;
while(ha < ta || hb < tb){
if(ha == ta || (hb < tb && check_ab(dqa[ha], dqa[ha + 1], dqb[hb], dqb[hb + 1]))){
ans += LL(dqb[hb + 1] - dqb[hb]) * a[dqa[ha]];
hb++;
}else{
ans += LL(dqa[ha + 1] - dqa[ha]) * b[dqb[hb]];
ha++;
}
}
cout << ans;
return 0;
}
luogu - P4139 上帝与集合的正确用法
题目也就是要求,\(2^{2^{2^{\cdots}}} \bmod m\)。直接利用扩展欧拉定理 \(a^b \bmod m = a^{b \bmod \varphi(m)+\varphi(m)} \bmod m\) 降幂即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int f[10000003], vis[10000003];
LL qpow(LL A, LL B, LL mod){
LL ret = 1;
while(B > 0){
if(B & 1) ret = ret * A % mod;
A = A * A % mod, B >>= 1;
}
return ret;
}
LL Get(LL mod){
if(mod == 1) return 1;
return qpow(2, Get(f[mod]) + f[mod], mod);
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
for(int i = 1; i <= 1e7; i++) f[i] = i;
for(int i = 2; i <= 1e7; i++){
if(vis[i]) continue;
for(int j = i; j <= 1e7; j += i){
vis[j] = 1, f[j] = f[j] / i * (i - 1);
}
}
int T;
cin >> T;
while(T--){
LL mod;
cin >> mod;
cout << Get(mod) << "\n";
}
return 0;
}
CF185D - Visit of the Great
大致思路:推导出 \(\gcd \in {1,2}\),再推导出乘积。其中推 \(\gcd\) 的方法用到了设 \(d=\gcd\),然后解同余。
题解:https://www.luogu.com.cn/article/ui5ywks4
题解已经非常详细了。。。补充:
- \(\sum\limits_{i=0}^{n}{x^i} = \dfrac{1 - x^{n+1}}{1 - x}\)
- 这题的细节有些多,需要特判一些东西
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
LL qpow(LL A, LL B, LL mod){
LL ret = 1;
while(B > 0){
if(B & 1) ret = ret * A % mod;
A = A * A % mod, B >>= 1;
}
return ret;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
int T;
cin >> T;
while(T--){
LL k, l, r, mod;
cin >> k >> l >> r >> mod;
if(mod == 2){
cout << (k % 2 == 1 ? 0 : 1) << "\n";
continue;
}
LL ans = 1;
LL fi = ((k%mod==0 ? 0 : qpow(k, qpow(2, r + 1, mod - 1), mod)) - 1 + mod) % mod;
LL se = ((k%mod==0 ? 0 : qpow(k, qpow(2, l, mod - 1), mod)) - 1 + mod) % mod;
if(se == 0){
ans = qpow(2, r - l + 1, mod);
}else{
ans = fi * qpow(se, mod - 2, mod) % mod;
}
if(k & 1) ans = ans * qpow(qpow(2, r - l, mod), mod - 2, mod) % mod;
cout << ans << "\n";
}
return 0;
}
CF906D - Power Tower
欧拉函数每取两次会至少减半。然后就是需要注意细节,这题利用扩展欧拉定理需要判断是否 \(< \varphi(mod)\),有个实现细节,可以看代码注释。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
map<int, int> mp;
int F(int x){
if(mp.find(x) != mp.end()) return mp[x];
int ret = x, _x = x;
for(int i = 2; i * i <= x; i++){
if(x % i == 0) ret = ret / i * (i - 1);
while(x % i == 0) x /= i;
}
if(x > 1) ret = ret / x * (x - 1);
return mp[_x] = ret;
}
int n, Q, w[100003];
LL MOD(LL x, LL mod){
return (x < mod ? x : x % mod + mod); // 再这里提前 +mod,后面就不用判了
}
LL qpow(LL A, LL B, LL mod){
LL ret = 1;
while(B > 0){
if(B & 1) ret = MOD(ret * A, mod);
A = MOD(A * A, mod), B >>= 1;
}
return ret;
}
LL QUE(int l, int r, LL mod){
if(l == r || mod == 1) return MOD(w[l], mod);
return qpow(w[l], QUE(l + 1, r, F(mod)), mod);
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
int mod;
cin >> n >> mod;
for(int i = 1; i <= n; i++){
cin >> w[i];
}
cin >> Q;
while(Q--){
int l, r;
cin >> l >> r;
cout << QUE(l, r, mod) % mod << "\n";
}
return 0;
}
luogu - P9150 邮箱题
这题一定是构成几个环,然后按照环上的顺序走。
首先考虑暴力做法:
- 枚举起点
- 找到环上的下一个点,插入
CF1028G - Guess the number
注意这个限制:\(k>x\) 就直接失败
类似二分的方法明显不可靠了。没想到这题可以 dp!!!
\(dp_{d,l}\) 表示最长的长度 \(len\),满足 \(d\) 次询问可以求出 \(x\in [l,l+len-1]\) 中的 \(x\)。
普通转移。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const LL M = 10004205361450474;
LL dp[6][10003];
void init(){
for(int d = 1; d <= 5; d++){
for(int l = 1; l <= 10000; l++){
LL r = min(l + dp[d - 1][l] + 1, 1ll * 10000);
dp[d][l] = dp[d - 1][l];
for(int k = 1; k <= l; k++){
if(r == 10000){ // 这里只是为了优化常数
dp[d][l] += (dp[d - 1][r] + 1) * (l - k + 1);
break;
}
dp[d][l] += dp[d - 1][r] + 1;
r = min(r + dp[d - 1][r] + 1, 1ll * 10000);
}
}
}
}
int main(){
init();
LL now = 1;
for(int d = 5; d >= 1; d--){
vector<LL> vt;
LL r = now;
for(int k = 1; k <= min(now, 1ll * 10000); k++){
r += dp[d - 1][min(r, 1ll * 10000)];
if(r > M) break;
vt.push_back(r);
r++;
}
cout << vt.size() << "\n";
for(LL x : vt) cout << x << " ";
cout << endl;
int pos; cin >> pos;
if(pos < 0) return 0;
if(pos) now = vt[pos - 1] + 1;
}
return 0;
}
https://www.luogu.com.cn/problem/CF1603E
https://www.luogu.com.cn/problem/P8340
https://www.luogu.com.cn/problem/P9338
https://www.luogu.com.cn/problem/P9330
https://www.luogu.com.cn/problem/CF1466I
https://www.luogu.com.cn/problem/CF1028G
https://www.luogu.com.cn/problem/P10786
https://www.luogu.com.cn/problem/P9338
P3986 斐波那契数列
数学题。没用到什么知识,除了 \(\gcd(F(x),F(x-1)) = 1\) 和 exgcd。可以自己动手试一试。
参考题解:https://www.luogu.com.cn/article/mbxmuex3
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
using i128 = __int128_t;
struct Exgcd{ // 拓展欧几里得模板
LL x, y;
LL gcd(LL a, LL b){ return !b ? a : gcd(b, a % b); }
void exgcd(LL a, LL b){
if(!b){ x = 1, y = 0; return; }
exgcd(b, a % b);
LL t = x; x = y, y = t - (a / b) * y;
}
bool Find(LL &w, LL d, LL p){ // 求解 wx + dy = p,0表示无解
if(p % gcd(w, d) != 0) return 0;
exgcd(w, d); LL r = p / gcd(w, d); x = (i128)x * r % d, y = (i128)y * r % d;
x = (x + d) % d;
w = x, d = y; return 1;
}
LL I(LL x, LL mod){ // 求逆元
Find(x, mod, 1);
return x;
}
}exgcd;
LL k, dp[50];
int main(){
ios::sync_with_stdio(0), cin.tie(0);
dp[0] = 1, dp[1] = 1;
cin >> k;
LL ans = 0;
for(int d = 2; ; d++){
if(dp[d - 1] > k) break;
LL M = exgcd.I(dp[d - 2], dp[d - 1]) * k % dp[d - 1];
LL R = ceil(1.0 * k / dp[d - 2]) - 1;
ans = (ans + R / dp[d - 1] + (M > 0 && R % dp[d - 1] >= M)) % LL(1e9 + 7);
dp[d] = dp[d - 1] + dp[d - 2];
}
cout << ans;
return 0;
}
SP10707 - COT2 - Count on a tree II
欧拉序原来这么有用。
得到欧拉序后,一些简单分类讨论+莫队。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 4e5 + 3, MAXL = 20;
struct Ask{
int l, r, lca, id;
}q[MAXN];
int n, k = 0, Q, st[MAXN], ed[MAXN], pos[MAXN];
int col[MAXN], anc[MAXL][MAXN], dep[MAXN];
vector<int> eg[MAXN];
int ans[MAXN], sum[MAXN], vis[MAXN];
void Insert(int c){
ans[0] += sum[c] == 0, sum[c]++;
}
void Erase(int c){
ans[0] -= sum[c] == 1, sum[c]--;
}
void Update(int i){
if(vis[i] == 0){
vis[i] = 1, Insert(col[i]);
}else{
vis[i] = 0, Erase(col[i]);
}
}
void dfs(int x, int dad){
st[x] = ++k, pos[k] = x;
anc[0][x] = dad, dep[x] = dep[dad] + 1;
for(int nxt : eg[x]){
if(nxt != dad) dfs(nxt, x);
}
ed[x] = ++k, pos[k] = x;
}
int LCA(int x, int y){
if(dep[x] > dep[y]) swap(x, y);
for(int len = dep[y] - dep[x], l = 0; l < MAXL; l++){
if((len >> l) & 1) y = anc[l][y];
}
if(x == y) return x;
for(int l = MAXL - 1; l >= 0; l--){
if(anc[l][x] != anc[l][y]) x = anc[l][x], y = anc[l][y];
}
return anc[0][x];
}
void init(){
cin >> n >> Q;
map<int, int> mp;
for(int i = 1, x, cnt = 0; i <= n; i++){
cin >> x;
if(mp.find(x) == mp.end()) mp[x] = ++cnt;
x = mp[x], col[i] = x;
}
for(int i = 1, U, V; i < n; i++){
cin >> U >> V, eg[U].push_back(V), eg[V].push_back(U);
}
dfs(1, 0);
for(int l = 1; l < MAXL; l++){
for(int i = 1; i <= n; i++) anc[l][i] = anc[l-1][anc[l-1][i]];
}
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
init();
for(int i = 1, x, y; i <= Q; i++){
cin >> x >> y;
int lca = LCA(x, y);
if(lca == x || lca == y){
if(dep[x] > dep[y]) swap(x, y);
q[i].lca = -1, q[i].l = st[x], q[i].r = st[y], q[i].id = i;
continue;
}
if(ed[x] > st[y]) swap(x, y);
q[i].lca = lca, q[i].l = ed[x], q[i].r = st[y], q[i].id = i;
}
int B = sqrt(k);
B = max(1, B);
sort(q + 1, q + 1 + Q, [&B](Ask i, Ask j){
if(i.l / B == j.l / B){
return i.r < j.r;
}
return i.l / B < j.l / B;
});
for(int i = 1, l = 1, r = 0; i <= Q; i++){
for(; l > q[i].l; l--, Update(pos[l]));
for(; r < q[i].r; r++, Update(pos[r]));
for(; l < q[i].l; Update(pos[l]), l++);
for(; r > q[i].r; Update(pos[r]), r--);
if(q[i].lca > 0) Insert(col[q[i].lca]);
ans[q[i].id] = ans[0];
if(q[i].lca > 0) Erase(col[q[i].lca]);
}
for(int i = 1; i <= Q; i++){
cout << ans[i] << "\n";
}
return 0;
}
luogu - P3473 [POI2008] UCI-The Great Escape
首先一定是这样的走法:
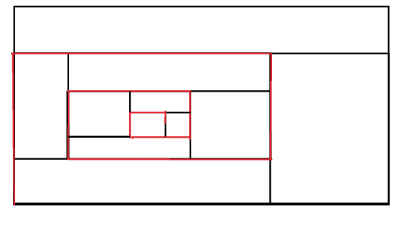
发现就是将大矩形分为多个小矩形。然后就是二维区间 dp,分四种情况讨论。注意需要滚动优化空间。
sb错误:注意 + 的优先级比 == 高
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
int n, m, mod;
LL dp[105][105][105][2][4];
int s1[103][103], s2[103][103];
char ch[103][103];
void ADD(LL &x, LL y){
x += y;
if(x >= mod) x -= mod;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m >> mod;
int Sx, Sy; cin >> Sx >> Sy, swap(Sx, Sy);
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
cin >> ch[i][j];
s1[i][j] = s1[i][j - 1] + (ch[i][j] == '*');
s2[i][j] = s2[i - 1][j] + (ch[i][j] == '*');
}
}
int f = 0;
for(int o = 0; o < 4; o++) dp[Sx][Sx][Sy][f][o] = 1;
LL ans = 0;
for(int len1 = 1; len1 <= m; len1++){ // 扩散型
for(int u = 1; u <= n; u++){
for(int d = u; d <= n; d++){
for(int l = 1; l <= m; l++) for(int o = 0; o < 4; o++) dp[u][d][l][f^1][o] = 0;
}
}
for(int l = 1; l <= m - len1 + 1; l++){
int r = l + len1 - 1;
for(int len2 = 1; len2 <= n; len2++){
for(int u = 1; u <= n - len2 + 1; u++){
int d = u + len2 - 1;
if(r < m && ch[d][r + 1] == '+'){
ADD(dp[u][d][l][f^1][0], dp[u][d][l][f][0]);
if(s2[d][r + 1] == s2[u - 1][r + 1]){
ADD(dp[u][d][l][f^1][1], dp[u][d][l][f][0]);
}
}
if(u > 1 && ch[u - 1][r] == '+'){
ADD(dp[u - 1][d][l][f][1], dp[u][d][l][f][1]);
if(s1[u - 1][r] == s1[u - 1][l - 1]){
ADD(dp[u - 1][d][l][f][2], dp[u][d][l][f][1]);
}
}
if(l > 1 && ch[u][l - 1] == '+'){
ADD(dp[u][d][l - 1][f^1][2], dp[u][d][l][f][2]);
if(s2[d][l - 1] == s2[u - 1][l - 1]){
ADD(dp[u][d][l - 1][f^1][3], dp[u][d][l][f][2]);
}
}
if(d < n && ch[d + 1][l] == '+'){
ADD(dp[u][d + 1][l][f][3], dp[u][d][l][f][3]);
if(s1[d + 1][r] == s1[d + 1][l - 1]){
ADD(dp[u][d + 1][l][f][0], dp[u][d][l][f][3]);
}
}
if(d == n && l == 1) ADD(ans, dp[u][d][l][f][3]);
}
}
}
f ^= 1;
}
cout << ans;
return 0;
}
/*
5 5 10007
3 3
++++*
+++++
+*+++
*++++
+++++
5 5 10007
3 5
++++*
+++++
+*+++
*++++
+++++
*/
luogu - P1776 宝物筛选
单调队列优化多重背包模板。
看代码可能更好懂。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int n, W;
LL f[2][400003];
deque<int> dq;
int main(){
cin >> n >> W;
int o = 0;
LL _ans = 0;
for(int i = 1, v, w, m; i <= n; i++){
cin >> v >> w >> m;
if(!w){
_ans += 1ll * m * v;
continue;
}
for(int y = 0; y < w; y++){
deque<int> ().swap(dq);
for(int x = 0; x * w + y <= W; x++){
while(!dq.empty() && x - dq.front() > m) dq.pop_front();
while(!dq.empty() && f[o][dq.back() * w + y] - 1ll * dq.back() * v < f[o][x * w + y] - 1ll * x * v) dq.pop_back();
dq.push_back(x);
f[o^1][x * w + y] = f[o][dq.front() * w + y] - 1ll * dq.front() * v + 1ll * x * v;
}
}
o ^= 1;
}
cout << f[o][W] + _ans;
return 0;
}
/*
20 300
18 30 3
2 20 2
19 16 1
3 25 5
13 12 4
1 22 1
11 2 5
3 26 9
10 29 6
4 13 2
15 8 2
10 1 3
16 25 1
16 5 8
11 8 9
13 21 4
16 4 9
17 16 2
13 27 1
6 20 8
607
*/
CF372C - Watching Fireworks is Fun
普通的单调队列优化 dp。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1.5e5 + 3, MAXM = 300 + 3;
int n, m, d;
LL f[2][MAXN];
int main(){
cin >> n >> m >> d;
int o = 0;
deque<int> dq;
for(int i = 1, a, b, t, lt = 1; i <= m; i++){
cin >> a >> b >> t, t = t - lt;
lt += t;
deque<int> ().swap(dq);
for(int i = 1; i <= n; i++) f[o^1][i] = -1e18;
for(int i = 1; i <= min(1ll * n, 1ll + 1ll * t * d); i++){
while(!dq.empty() && f[o][i] > f[o][dq.back()]) dq.pop_back();
dq.push_back(i);
}
for(int i = 1; i <= n; i++){
while(!dq.empty() && dq.front() < i - 1ll * t * d) dq.pop_front();
LL p = i + 1ll * t * d;
if(i > 1 && p <= n){
while(!dq.empty() && f[o][p] > f[o][dq.back()]) dq.pop_back();
dq.push_back(p);
}
f[o^1][i] = f[o][dq.front()] + b - abs(i - a);
}
o ^= 1;
}
LL ans = -1e18;
for(int i = 1; i <= n; i++) ans = max(ans, f[o][i]);
cout << ans;
return 0;
}
[AGC005C] Tree Restoring
构造题。
直径性质:离任意一个点最远的点,一定是直径两端点中的一个。直径为 \(len=\max{a_i} + 1\)。
首先把直径造出来,考虑将剩余点挂在直径上,由于剩余的 \(a_i \le len - 1\),发现没有必要将一个点挂在另外一个点上,直接挂直径上即可。
如果那些太小的点就没有可以挂的地方,就无解。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e5 + 3;
int n, cnt[MAXN];
void No(){ cout << "Impossible"; exit(0); }
int main(){
cin >> n;
int mx = 0;
for(int i = 1, x; i <= n; i++){
cin >> x, cnt[x]++, mx = max(mx, x);
}
mx++;
for(int i = mx - 1; i >= mx / 2; i--) cnt[i] -= 2;
if(mx & 1) cnt[mx / 2]++;
for(int i = 0; i <= n; i++){
if(cnt[i] < 0) No();
}
for(int i = 0; i <= mx / 2; i++){
if(cnt[i] > 0) No();
}
cout << "Possible";
return 0;
}
CF1442E - Black, White and Grey Tree
这题的 dp 部分似乎是错误的理解,具体可以见洛谷讨论区,撂这了,有空再看
转化部分参考题解:https://www.luogu.com.cn/article/rsa9b266
考虑没有灰色,如何求答案。贪心地,问题可以变为:确定一个起点,对树分层,最小化最大层数。
这个问题还是太复杂,注意有一种很好的转化:如果两端点不同色,则边权为 \(1\),否则为 \(0\),求直径 \(len\),答案为 \(\left\lceil \frac{len}{2} \right\rceil + 1\)
再来考虑灰点,使用 dp。
luogu - P6891 [JOISC2020] ビルの飾り付け 4
现有 \(O(n^2)\) 的 01 背包暴力:\(f_{i,j,0/1}\) 表示前 \(i\) 个,有 \(j\) 个 \(A\),最后一个是选什么。
01 背包有些什么性质呢?不妨设 \(s_{i,0/1}\) 表示满足 \(f_{i,j,0/1}=1\) 的 \(j\) 的集合。
发现每个集合的 \(j\) 都是连续一段(听说证明很复杂,就不证明了,主要是为了理解 01 背包的一些小优化)。然后 \(O(n)\) 就没了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e6 + 3;
struct Edge{
int l, r;
void ADD(){ l++, r++; }
}dp[MAXN][2];
int n, a[MAXN][2];
void ADD(Edge &x, Edge e, int o){
if(o == 0) e.ADD();
x.l = min(x.l, e.l), x.r = max(x.r, e.r);
}
bool check(Edge e, int p){
return e.l <= p && p <= e.r;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n, n *= 2;
for(int i = 1; i <= n; i++){
cin >> a[i][0];
}
for(int i = 1; i <= n; i++){
cin >> a[i][1];
}
for(int i = 0; i <= n; i++){
for(int o = 0; o < 2; o++) dp[i][o] = {int(1e9), -int(1e9)};
}
dp[0][0] = dp[0][1] = {0, 0};
for(int i = 1; i <= n; i++){
for(int o = 0; o < 2; o++){
if(a[i][o] >= a[i - 1][o]) ADD(dp[i][o], dp[i - 1][o], o);
if(a[i][o] >= a[i - 1][o^1]) ADD(dp[i][o], dp[i - 1][o^1], o);
}
}
if(!check(dp[n][0], n / 2) && !check(dp[n][1], n / 2)){
cout << -1;
return 0;
}
string s = "";
for(int i = n, x = n / 2, la = 1e9; i >= 1; i--){
if(x > 0 && check(dp[i][0], x) && a[i][0] <= la){
x--, s.push_back('A'), la = a[i][0];
}else s.push_back('B'), la = a[i][1];
}
reverse(s.begin(), s.end()), cout << s;
return 0;
}
[AT_dp_y]Grid 2
考虑容斥,变为求经过至少一个黑点的路径数。
对于一条至少一个黑点的路径,考虑用路径上第一个黑点来替代。
设 \(f_i\) 表示最终到达 \(i\) 号点,且不经过其余黑点的路径数。
答案为 \(总路径数 - \sum{f_i \dbinom{n - x_i + m - y_i}{n - x_i}}\)。转移和求答案是一样的。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const LL mod = 1e9 + 7;
const int MAXN = 2e5 + 3;
LL qpow(LL A, LL B){
LL ret = 1;
while(B > 0){
if(B & 1) ret = ret * A % mod;
A = A * A % mod, B >>= 1;
}
return ret;
}
LL fac[MAXN], ifac[MAXN];
int h, w, n;
LL f[MAXN];
PII a[MAXN];
LL C(int A, int B){ return fac[B] * ifac[A] % mod * ifac[B - A] % mod; }
LL S(PII i, PII j){ return C(j.first - i.first, j.first - i.first + j.second - i.second); }
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> h >> w >> n;
ifac[0] = fac[0] = 1;
for(int i = 1; i <= 2e5; i++) fac[i] = fac[i - 1] * i % mod, ifac[i] = qpow(fac[i], mod - 2);
for(int i = 1; i <= n; i++){
cin >> a[i].first >> a[i].second;
}
sort(a + 1, a + 1 + n);
LL ans = S({1, 1}, {h, w});
for(int i = 1; i <= n; i++){
f[i] = 0;
for(int j = 1; j < i; j++){
if(a[j].second > a[i].second) continue;
f[i] += S(a[j], a[i]) * f[j] % mod;
f[i] %= mod;
}
f[i] = (S({1, 1}, a[i]) - f[i] + mod) % mod;
ans = (ans - S(a[i], {h, w}) * f[i] % mod + mod) % mod;
}
cout << ans;
return 0;
}
luogu - P8820 [CSP-S 2022] 数据传输
首先注意:\(k=3\) 时,不一定只经过链上的点。(今天猴急了,写了个错解浪费 1.5h)
参考题解:https://www.luogu.com.cn/article/dqtao6yd
对于 \(k\le2\) 的情况一定只经过链上的点,是简单的,先考虑 \(k=3\)。
分情况讨论,列出 dp 式子,然后化简乘 \(\min\) 矩阵乘法 可以优化的样例。具体见题解。
然后就是 \(\min\) 矩阵乘法优化了。
注意这题必须取 \(s,t\),实现有些细节。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 2e5 + 3, MAXL = 20;
const LL inf = 1e18;
int n, Q, k;
LL val[MAXN], num[MAXN];
vector<int> eg[MAXN];
int anc[MAXN][MAXL], dep[MAXN];
struct Matrix{
LL a[3][3];
Matrix operator* (Matrix _) const {
Matrix ret;
for(int i = 0; i < 3; i++){
for(int j = 0; j < 3; j++){
ret.a[i][j] = inf;
for(int h = 0; h < 3; h++){
ret.a[i][j] = min(ret.a[i][j], a[i][h] + _.a[h][j]);
}
}
}
return ret;
}
void A(){
for(int i = 0; i < 3; i++) for(int j = 0; j < 3; j++) a[i][j] = inf;
}
void _A(){
A();
for(int i = 0; i < 3; i++) a[i][i] = 0;
}
}pre[MAXN][MAXL], suf[MAXN][MAXL];
Matrix Get(int x){
Matrix ret;
ret.A();
if(k == 1){
ret.a[0][0] = val[x], ret.a[1][1] = ret.a[2][2] = 0;
}else if(k == 2){
ret.a[0][0] = ret.a[1][0] = val[x], ret.a[0][1] = ret.a[2][2] = 0;
}else{
ret.a[0][0] = ret.a[1][0] = ret.a[2][0] = val[x];
ret.a[0][1] = ret.a[1][2] = 0, ret.a[1][1] = num[x], ret.a[2][1] = num[x] + val[x];
}
return ret;
}
void dfs(int x, int dad){
anc[x][0] = dad, dep[x] = dep[dad] + 1, num[x] = inf;
for(int nxt : eg[x]){
num[x] = min(num[x], val[nxt]);
if(nxt != dad) dfs(nxt, x);
}
pre[x][0] = suf[x][0] = Get(x);
}
Matrix Solve(int x, int y){
bool o = 0;
Matrix retp, rets; retp._A(), rets._A();
if(dep[x] < dep[y]) rets = suf[y][0] * rets, y = anc[y][0];
for(int len = dep[x] - dep[y], l = 0; l < MAXL; l++){
if((len >> l) & 1) retp = retp * pre[x][l], x = anc[x][l];
}
if(x == y) return retp * pre[x][0] * rets;
for(int l = MAXL - 1; l >= 0; l--){
if(anc[x][l] != anc[y][l]){
retp = retp * pre[x][l], rets = suf[y][l] * rets, x = anc[x][l], y = anc[y][l];
}
}
return retp * pre[x][0] * pre[anc[x][0]][0] * pre[y][0] * rets;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> Q >> k;
for(int i = 1; i <= n; i++) cin >> val[i];
for(int i = 1, U, V; i < n; i++) cin >> U >> V, eg[U].push_back(V), eg[V].push_back(U);
for(int i = 0; i <= n; i++) for(int l = 0; l < MAXL; l++) suf[i][l]._A(), pre[i][l]._A();
dfs(1, 0);
for(int l = 1; l < MAXL; l++){
for(int i = 1; i <= n; i++){
anc[i][l] = anc[anc[i][l-1]][l-1];
suf[i][l] = suf[anc[i][l-1]][l-1] * suf[i][l-1];
pre[i][l] = pre[i][l-1] * pre[anc[i][l-1]][l-1];
}
}
while(Q--){
int x, y; cin >> x >> y;
if(x == y){
cout << val[x] << "\n";
continue;
}
if(dep[x] < dep[y]) swap(x, y);
Matrix ans; ans.A();
ans.a[0][0] = val[x];
if(k == 3) ans.a[0][1] = val[x] + num[x];
ans = ans * Solve(anc[x][0], y);
cout << ans.a[0][0] << "\n";
}
return 0;
}
luogu - P9870 [NOIP2023] 双序列拓展
首先这题平方暴力是简单的。
参考题解:https://www.luogu.com.cn/article/di5ogaa0
当你写出了 dp,发现问题可以转化为:对于一个网格图,那些 \(x_i \ge y_j\) 的点 \((i,j)\) 为障碍,满足 \((1,1)\) 和 \((n,m)\) 八联通。
(这个转化有些难,也是最关键一步,如果不能直接看出来,可以通过 dp 方程看出来)
对于每一行,\(y_j \le x_i\) 的 \(j\) 构成一个集合,显然所有集合只有可能 包含或相等。
所以起点和终点不联通只有四种情况:
- 一行直接切开。
- 一列直接切开。
- 一个 L 形困住 \((1,1)\)。
- 一个 L 形困住 \((n,m)\)。
由于第三种和四种类似。具体看参考题解。
也就是存在 \((i,j)\) 满足 \(x_i \ge \max_{k=1}^{j}{y_k}\) 且 \(y_i \le \min_{k=1}^{i}{x_k}\)。
发现两式可以合并,得到 \(\min_{k=1}^{i}{x_k} \le \max_{k=1}^{j}{y_k}\)。这是有单调性的,可以双指针。
luogu - P3443 [POI2006] LIS-The Postman
如果这题没有最后一个限制,就是普通的求有向图欧拉回路。
最后一个限制相当于:给一些边规定下一条走的边。所以我们可以直接在原图中删去这条边,边于边之间连边。
本题的难度在于想到将限制连边。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 2e5 + 3;
int n, m, to[MAXN], nex[MAXN], deg[MAXN], evis[MAXN], _evis[MAXN];
vector<PII> eg[MAXN];
vector<int> ans;
map<int, int> chk[MAXN];
void No(){ cout << "NIE"; exit(0); }
void dfs(int x, int E){
if(E > 0){
if(_evis[E]) No();
_evis[E] = 1, dfs(to[E], nex[E]);
}else{
while(!eg[x].empty()){
PII e = eg[x].back(); eg[x].pop_back();
if(evis[e.second]) continue;
evis[e.second] = 1, dfs(e.first, nex[e.second]);
}
}
ans.push_back(x);
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
for(int i = 1, U, V; i <= m; i++){
cin >> U >> V, to[i] = V, eg[U].push_back({V, i});
deg[U]++, deg[V]--, chk[U][V] = i;
}
for(int i = 1; i <= n; i++){
if(deg[i] != 0) No();
}
int T;
cin >> T;
while(T--){
int x, y, z, k, id = 0, laid = 0;
cin >> k >> x >> y, k -= 2;
laid = chk[x][y];
if(!laid) No();
while(k--){
cin >> z, id = chk[y][z];
if(!id) No();
if(nex[laid] && nex[laid] != id) No();
nex[laid] = id;
evis[id] = 1;
x = y, y = z, laid = id;
}
}
dfs(1, 0);
if(ans.size() != m + 1) No();
cout << "TAK\n";
for(int i = ans.size() - 1; i >= 0; i--) cout << ans[i] << "\n";
return 0;
}
CF1634E - Fair Share
如果一个值总出现次数为奇数,就直接不合法。
考虑建图,试着转化。每个值,在一个数组中出现一次,数组和值就连一条无向边。发现这个图满足每个点的度数为偶数。
考虑欧拉回路。欧拉回路可以给每个点分成入读=出度。也就是平分。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 3e5 + 3;
map<int, int> mp;
int tot = 0;
LL read(){
int x; cin >> x;
if(mp.find(x) == mp.end()) mp[x] = ++tot;
return mp[x];
}
int n, m, deg[MAXN];
vector<PII> eg[MAXN];
vector<int> ans[MAXN];
void No(){ cout << "NO"; exit(0); }
map<int, int> emp[MAXN];
void dfs(int x){
while(!eg[x].empty()){
PII e = eg[x].back(); eg[x].pop_back();
int _x = min(x, e.first);
if(emp[e.second][_x]) continue;
emp[e.second][_x] = 1;
if(x <= m) ans[x][e.second] = 1;
dfs(e.first);
}
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> m, tot = m;
for(int i = 1, l, x; i <= m; i++){
cin >> l, ans[i].resize(l + 1);
for(int j = 1; j <= l; j++){
ans[i][j] = 0;
x = read(), eg[x].push_back({i, j}), eg[i].push_back({x, j}), deg[i]++, deg[x]++;
}
}
for(int i = 1; i <= tot; i++) if(deg[i] & 1) No();
for(int i = 1; i <= tot; i++){
dfs(i);
}
cout << "YES\n";
for(int i = 1; i <= m; i++){
for(int j = 1; j < ans[i].size(); j++) cout << (ans[i][j] ? "L" : "R");
cout << "\n";
}
return 0;
}
CF547D - Mike and Fish
考虑建图。每个点作一条边,连接横坐标和纵坐标。
问题转化为需要给每条边定向,是的每个节点的出入和入读之差在 \(1\) 及以内。
有些点的度数不是偶数,但是发现度数为奇数的点只有偶数个,可以向 \(0\) 连边。欧拉回路然后就做完了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 4e5 + 3, V = 4e5;
int n, deg[MAXN], evis[MAXN], ans[MAXN];
vector<PII> eg[MAXN];
void dfs(int x){
while(!eg[x].empty()){
PII e = eg[x].back(); eg[x].pop_back();
if(evis[e.second]) continue;
evis[e.second] = 1;
if(e.second <= n){
if(x <= 2e5){
ans[e.second] = 1;
}
}
dfs(e.first);
}
}
int main(){
cin >> n;
for(int i = 1, x, y; i <= n; i++){
cin >> x >> y, y += 2e5;
eg[x].push_back({y, i}), eg[y].push_back({x, i}), deg[x]++, deg[y]++;
}
for(int i = 1, c = 0; i <= V; i++){
if(deg[i] & 1) c++, eg[0].push_back({i, n + c}), eg[i].push_back({0, n + c});
}
for(int i = 1; i <= V; i++) dfs(i);
for(int i = 1; i <= n; i++) cout << (ans[i] == 1 ? "b" : "r");
return 0;
}
CF62D - Wormhouse
因为 \(n \ge 3\),所以起点是一定等于 \(a_1\) 的。
然后直接暴力搜索。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 2000 + 3;
int n, m, a[MAXN], evis[MAXN];
vector<PII> eg[MAXN];
vector<int> ans;
void dfs(int x, int o1){
if(ans.size() == m + 1){
if(o1 == 0) return;
for(int y : ans) cout << y << " ";
exit(0);
return;
}
for(int i = 0; i < eg[x].size(); i++){ PII e = eg[x][i];
if(evis[e.second]) continue;
if(!o1 && e.first < a[ans.size() + 1]) continue;
evis[e.second] = 1;
ans.push_back(e.first);
dfs(e.first, o1 | (e.first > a[ans.size()]));
ans.pop_back();
evis[e.second] = 0;
}
}
int main(){
cin >> n >> m;
for(int i = 1; i <= m + 1; i++){
cin >> a[i];
if(i > 1) eg[a[i]].push_back({a[i - 1], i - 1}), eg[a[i - 1]].push_back({a[i], i - 1});
}
for(int i = 1; i <= n; i++) sort(eg[i].begin(), eg[i].end());
ans.push_back(a[1]);
dfs(a[1], 0);
cout << "No solution";
return 0;
}
luogu - P10766 「CROI · R2」01-string
- 先翻转再赋值:两种操作的区间一定可以不交
- 先赋值再赋值:两种操作的区间一定可以不交
- 先翻转再翻转:两种操作的区间一定可以不交
所以一个位置 \(i\) 一共有六种操作。
- \(0\):不变
- \(1\):赋值 \(0\)
- \(2\):赋值 \(1\)
- \(3\):翻转
- \(4\):先赋值 \(0\),再翻转
- \(5\):先赋值 \(1\),再翻转
所以状态 \(f_{i,0/1/2/3/4/5}\),普通转移。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 5e5 + 3;
int n;
string s, t;
int dp[MAXN][6];
int main(){
int T;
cin >> T;
while(T--){
cin >> s >> t, n = s.size(), s = " " + s, t = " " + t;
for(int i = 0; i <= n; i++) for(int o = 0; o < 6; o++) dp[i][o] = 1e9;
dp[0][0] = 0, dp[0][1] = dp[0][2] = dp[0][3] = 1, dp[0][4] = dp[0][5] = 2;
for(int i = 1; i <= n; i++){
int S = s[i] - '0', T = t[i] - '0';
int f0 = dp[i - 1][0], f1 = dp[i - 1][1], f2 = dp[i - 1][2], f3 = dp[i - 1][3], f4 = dp[i - 1][4], f5 = dp[i - 1][5];
if((S ^ 1) == T) dp[i][3] = min({f0+1, f1+1, f2+1, f3, f4, f5});
else dp[i][0] = min({f0, f1, f2, f3, f4, f5});
if(T == 0) dp[i][1] = min({f0+1, f1, f2+1, f3+1, f4, f5+1});
else dp[i][2] = min({f0+1, f1+1, f2, f3+1, f4+1, f5});
if(T == 1) dp[i][4] = min({f0+2, f1+1, f2+2, f3+1, f4, f5+1});
else dp[i][5] = min({f0+2, f1+2, f2+1, f3+1, f4+1, f5});
}
cout << min({dp[n][0], dp[n][1], dp[n][2], dp[n][3], dp[n][4], dp[n][5]}) << "\n";
}
return 0;
}
luogu - P11190 「KDOI-10」反回文串
首先这题就是构造题。
参考题解:https://www.luogu.com.cn/article/2soxm7mk
若最大出现次数小于等于 \(\frac{n}{2}\)。
- 按照字符大小排序,然后 \(p[i]\) 和 \(p[i+\left\lfloor \frac{n}{2} \right\rfloor ]\) 一组。
- 若 \(n\) 为奇数,就把 \(p[n]\) 加入第一组。
若最大出现次数大于 \(\frac{n}{2}\)。设该字符为 \(c\)。
- 如果全部同一个字符就无解
- 如果就一个不同的字符
- \(n\) 为奇数且那个字符在正中间,则无解
- 否则全部设为一组
- 如果有至少两个不同的字符
- 左侧第一个不同的字符 \(l\),和右侧第一个不同的字符 \(r\)。提前将所有 \(c\) 的位置分配给 \(l,r\)。
- 枚举中间的每个不同的字符,从 \(l\) 和 \(r\) 中分配出来。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e5 + 3;
int n, cnt[26], p[MAXN];
string s;
int tot = 0;
set<int> st[MAXN];
void work(){
for(int i = 0; i < 26; i++) cnt[i] = 0;
for(int i = 1; i <= n; i++) cnt[s[i] - 'a']++;
int c, mx = 0;
for(int i = 0; i < 26; i++){
if(cnt[i] > mx) mx = cnt[i], c = i;
}
if(mx <= n / 2){
for(int i = 1; i <= n; i++) p[i] = i;
sort(p + 1, p + 1 + n, [](int i, int j){ return s[i] < s[j]; });
cout << "Huoyu\n" << n / 2 << "\n";
for(int i = 1; i <= n / 2; i++){
if(n % 2 == 1 && i == 1){
vector<int> vt; vt.push_back(p[i]), vt.push_back(p[i + n/2]), vt.push_back(p[n]);
sort(vt.begin(), vt.end());
cout << 3 << " ";
for(int x : vt) cout << x << " ";
cout << "\n";
continue;
}
cout << 2 << " " << min(p[i], p[i + n/2]) << " " << max(p[i], p[i + n/2]) << "\n";
}
return;
}
if(mx == n){
cout << "Shuiniao\n"; return;
}
if(mx == n - 1){
for(int i = 1; i <= n; i++) if(s[i] - 'a' != c) p[0] = i;
if(n % 2 == 1 && p[0] == n / 2 + 1){
cout << "Shuiniao\n"; return;
}
cout << "Huoyu\n";
cout << 1 << "\n" << n << "\n";
for(int i = 1; i <= n; i++) cout << i << " ";
cout << "\n";
return;
}
int l = 0, r = 0;
for(int i = 1; i <= n; i++){
if(l == 0 && s[i] - 'a' != c) l = i;
if(s[i] - 'a' != c) r = i;
}
tot = 2, st[1].clear(), st[2].clear();
cout << "Huoyu\n";
for(int i = l + 1; i <= n; i++){
if(i != r && s[i] - 'a' == c) st[1].insert(i);
}
for(int i = 1; i < l; i++){
if(i != r && s[i] - 'a' == c) st[2].insert(i);
}
for(int i = l + 1; i < r; i++){
if(s[i] - 'a' != c){
st[++tot].clear(), st[tot].insert(i);
if(st[1].size() > 1){
st[tot].insert(*st[1].begin()), st[1].erase(st[1].begin());
}else{
st[tot].insert(*st[2].begin()), st[2].erase(st[2].begin());
}
}
}
if(st[1].empty()) st[1].insert(*st[2].begin()), st[2].erase(st[2].begin());
if(st[2].empty()) st[2].insert(*st[1].begin()), st[1].erase(st[1].begin());
st[1].insert(l), st[2].insert(r);
cout << tot << "\n";
for(int i = 1; i <= tot; i++){
cout << st[i].size() << " ";
for(int x : st[i]) cout << x << " ";
cout << "\n";
}
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
int cid, T;
cin >> cid >> T;
while(T--){
cin >> n >> s, s = " " + s;
work();
}
return 0;
}
[ABC138F] Coincidence
题解:https://www.luogu.com.cn/article/kbeb2cs1
对于 \(x \le y\)。
- 若 \(2x \le y\),则 \(y - x > y \bmod x\)
- 若 \(2x > y\),则 \(y - x = y \bmod x\)
- 有 \(x \oplus y \ge y - x\)
所以 \(2x \le y\) 的可以直接忽略。进一步转化,可以得到 \(x\) 和 \(y\) 的二进制位数相同(具体看题解)。然后就是普通数位 dp。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const LL mod = 1e9 + 7;
LL L, R;
LL f[100][2][2][2];
LL Solve(int d, int o1, int o2, int o3){
if(d == -1) return 1;
if(f[d][o1][o2][o3] != -1) return f[d][o1][o2][o3];
LL ret = 0;
int O1 = (L >> d) & 1, O2 = (R >> d) & 1;
for(int i = (o1 ? 0 : O1); i < 2; i++){
for(int j = i; j <= (o2 ? 1 : O2); j++){
if(!o3 && i != j) continue;
ret += Solve(d - 1, o1 | (i != O1), o2 | (j != O2), o3 | (j != 0));
ret %= mod;
}
}
return f[d][o1][o2][o3] = ret;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
memset(f, -1, sizeof(f));
cin >> L >> R;
cout << Solve(60, 0, 0, 0);
return 0;
}
luogu - P3750 [六省联考 2017] 分手是祝愿
与其他题不同的是,这题 dp 状态设计考虑的是变化情况。
参考题解:https://www.luogu.com.cn/article/0nfti2gr
显然,每个按键都不可能被其他按键的组合键替代,于是我们实际上可以从大到小扫一遍,碰到亮的就按一遍,这样的话我们就可以找到所有必须要按的键,实际上就相当于除开这些键按了其他的键就还要必须按一个相同的键给按回来,这样我们就可以 dp 了。
\(f_i\) 表示 \(i\) 个要按的键变为 \(i-1\) 个要按的键的期望步数。
列出转移式子然后移项,再统计。具体看题解。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const LL mod = 1e5 + 3;
const int MAXN = 1e5 + 3;
LL qpow(LL A, LL B){
LL ret = 1;
while(B > 0){
if(B & 1) ret = ret * A % mod;
A = A * A % mod, B >>= 1;
}
return ret;
}
int n, k, a[MAXN];
LL f[MAXN];
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> k;
for(int i = 1; i <= n; i++) cin >> a[i];
int cnt = 0;
for(int i = n; i >= 1; i--){
if(!a[i]) continue;
cnt++;
for(int j = 1; j * j <= i; j++){
if(i % j == 0){
a[j] ^= 1;
if(i / j != j) a[i / j] ^= 1;
}
}
}
f[n] = 1;
for(int i = n - 1; i >= 1; i--){
f[i] = (n + f[i + 1] * (n - i) % mod) % mod * qpow(i, mod - 2) % mod;
}
LL ans = k;
if(cnt <= k){
ans = cnt;
}else{
for(int i = k + 1; i <= cnt; i++) ans = (ans + f[i]) % mod;
}
for(int i = 1; i <= n; i++) ans = ans * i % mod;
cout << ans;
return 0;
}
luogu - P5896 [IOI2016] aliens
参考题解:https://www.luogu.com.cn/article/kn8frljd
先考虑二维转一维。对于一个左上角 \((l,l)\) 右下角 \((r,r)\) 的正方形,如果一个点在其中,设 \(u=\min(i,j),v=\max(i,j)\),则 \(l \le u \le v \le r\)。
转化为了区间问题,但还是有些抽象,这里有个技巧:对于 \(u_1 \le u_2 \le v_2 \le v_1\),只要覆盖了 \(1\) 就覆盖了 \(2\)。(类似的 Trick https://www.luogu.com.cn/problem/P6047 )
所以删除多余区间后,按照 \(u\) 排序,则 \(v\) 也是递增的。然后就是 wqs 和 斜率优化 结合了。递推式也容易得到,具体看代码。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using LD = long double;
using PII = pair<LL, LL>;
const int MAXN = 1e5 + 4, MAXV = 1e6 + 3;
const LD eps = 1e-10;
int n, m, K;
PII a[MAXN];
vector<int> eg[MAXV];
int h = 1, t = 0, dq[MAXN];
LL f[MAXN], cnt[MAXN], x[MAXN], y[MAXN], k[MAXN];
LL P(LL w){ return w * w; }
LD Slope(int i, int j){
return LD(y[i] - y[j]) / LD(x[i] - x[j]);
}
bool check(LL D){
h = 1, t = 0, dq[++t] = 0, f[0] = 0, a[dq[h]].second = -1;
y[0] = D + P(a[1].first-1);
x[0] = a[1].first - 1;
for(int i = 1; i <= n; i++){
while(h < t && Slope(dq[h], dq[h + 1]) + eps <= k[i]) h++;
f[i] = f[dq[h]] - P(max(0ll, a[dq[h]].second - a[dq[h]+1].first + 1)) + P(a[i].second - a[dq[h]+1].first + 1) + D;
cnt[i] = cnt[dq[h]] + 1;
if(i == n) break;
x[i] = a[i+1].first-1, y[i] = f[i] - P(max(0ll, a[i].second-a[i+1].first+1)) + D + P(a[i+1].first-1);
while(h < t && Slope(dq[t - 1], dq[t]) >= Slope(dq[t], i) + eps) t--;
dq[++t] = i;
}
return cnt[n] <= K;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m >> K;
for(int i = 1, x, y; i <= n; i++){
cin >> x >> y, x++, y++;
int l = min(x, y), r = max(x, y);
eg[r].push_back(l);
}
n = 0;
for(int i = m, mil = 1e9; i >= 1; i--){
if(eg[i].empty()) continue;
sort(eg[i].begin(), eg[i].end());
if(eg[i][0] < mil) mil = eg[i][0], a[++n] = {mil, i};
}
sort(a + 1, a + 1 + n);
for(int i = 1; i <= n; i++){
k[i] = 2 * a[i].second;
}
LL l = 0, r = 1e13;
while(l < r){
LL mid = (l + r) >> 1;
if(check(mid)){
r = mid;
}else l = mid + 1;
}
check(l);
cout << f[n] - l * K;
return 0;
}
/*
f[i] = f[j] + (a[i].second - a[j+1].first + 1)^2 - max(0, a[j].second - a[j+1].first] + 1)^2 + D
f[i] = f[j] - max(0, a[j].second - a[j+1].first] + 1)^2 + D + a[i].second^2 + (a[j+1].first-1)^2 - 2 a[i].second (a[j+1].first-1)
f[i] - a[i].second^2 = f[j] - max(0, a[j].second - a[j+1].first] + 1)^2 + D + (a[j+1].first-1)^2 - 2 a[i].second (a[j+1].first-1)
b = y - kx
b = f[i] - a[i].second^2
y = f[j] - max(0, a[j].second - a[j+1].first] + 1)^2 + D + (a[j+1].first-1)^2
k = a[i].second * 2
x = (a[j+1].first-1)
*/
luogu - P2824 [HEOI2016/TJOI2016] 排序
二分答案,序列变为 01 序列。
然后可以直接线段树维护(支持区间赋值,区间求和)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e5 + 3;
int n, m, X;
int a[MAXN], op[MAXN], ql[MAXN], qr[MAXN];
int tr[MAXN * 4], lz[MAXN * 4];
void Down(int i, int l, int mid, int r){
if(lz[i] != -1){
lz[i * 2] = lz[i * 2 + 1] = lz[i];
tr[i * 2] = lz[i] * (mid - l + 1);
tr[i * 2 + 1] = lz[i] * (r - mid);
}
lz[i] = -1;
}
void Build(int i, int l, int r, int D){
lz[i] = -1;
if(l == r){
tr[i] = (a[l] >= D);
return;
}
int mid = (l + r) >> 1;
Build(i * 2, l, mid, D), Build(i * 2 + 1, mid + 1, r, D);
tr[i] = tr[i * 2] + tr[i * 2 + 1];
}
int Query(int i, int l, int r, int L, int R){
if(l == L && r == R) return tr[i];
int mid = (l + r) >> 1, ret = 0;
Down(i, l, mid, r);
if(L <= mid) ret += Query(i * 2, l, mid, L, min(mid, R));
if(mid + 1 <= R) ret += Query(i * 2 + 1, mid + 1, r, max(mid + 1, L), R);
return ret;
}
void Update(int i, int l, int r, int L, int R, int w){
if(l == L && r == R){
lz[i] = w, tr[i] = w * (r - l + 1);
return;
}
int mid = (l + r) >> 1;
Down(i, l, mid, r);
if(L <= mid) Update(i * 2, l, mid, L, min(mid, R), w);
if(mid + 1 <= R) Update(i * 2 + 1, mid + 1, r, max(mid + 1, L), R, w);
tr[i] = tr[i * 2] + tr[i * 2 + 1];
}
bool check(int D){
Build(1, 1, n, D);
for(int i = 1; i <= m; i++){
int c = Query(1, 1, n, ql[i], qr[i]), len = qr[i] - ql[i] + 1;
if(op[i] == 0){
if(c != len) Update(1, 1, n, ql[i], qr[i] - c, 0);
if(c != 0) Update(1, 1, n, qr[i] - c + 1, qr[i], 1);
}else{
if(c != 0) Update(1, 1, n, ql[i], ql[i] + c - 1, 1);
if(c != len) Update(1, 1, n, ql[i] + c, qr[i], 0);
}
}
return Query(1, 1, n, X, X) == 1;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; i++){
cin >> a[i];
}
for(int i = 1; i <= m; i++){
cin >> op[i] >> ql[i] >> qr[i];
}
cin >> X;
int l = 1, r = n;
while(l < r){
int mid = (l + r + 1) >> 1;
if(check(mid)){
l = mid;
}else r = mid - 1;
}
cout << l;
return 0;
}
luogu - P3449 [POI2006] PAL-Palindromes
这题有直接 Hash 退式子的做法 https://www.luogu.com.cn/article/3cpwu9v2 ,但是这题还可以利用一些美妙结论。
结论 1:一个回文串的循环节也是循环节。
- 这个证明是简单的,因为回文中心一定是可以平分循环节的。
结论 2:两个回文串可以拼接组成回文串,当且仅当两个回文串的最小循环节相同。
- 充分性:根据结论 1,这个证明比较显然。
- 必要性:设 \(s,t\) 的最小循环节分别为 \(x,y\) 且 \(|x| \le |y|\),又有 \(s+t\) 回文,所以 \(x\) 为 \(y\) 的循环节,但是 \(y\) 已经是最小循环节了,矛盾。
有了结论 2 后就可以直接做了。这里有个关于求最小循环节的 Trick:
- 求出前缀函数,由于字符串最短周期为 \(n - next[n]\)。
- 若 \(n \bmod (n - next[n]) = 0\) 则最小循环节长 \(n - next[n]\)。
- 否则长 \(n\)。
这种求法的证明可以感性理解一下。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 2e6 + 3;
int n, nex[MAXN];
string s[MAXN];
unordered_map<string, int> mp;
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
LL ans = 0;
for(int i = 1, l; i <= n; i++){
cin >> l >> s[i], s[i] = " " + s[i];
nex[1] = 0;
for(int j = 2, h = 0; j <= l; j++){
while(h > 0 && s[i][h + 1] != s[i][j]) h = nex[h];
h += (s[i][h + 1] == s[i][j]), nex[j] = h;
}
if(l % (l - nex[l]) == 0){
s[i] = s[i].substr(0, 1 + l - nex[l]);
}else{
s[i] = s[i];
}
mp[s[i]]++;
}
for(int i = 1; i <= n; i++) ans += mp[s[i]];
cout << ans;
return 0;
}
luogu - P3546 [POI2012] PRE-Prefixuffix
问题转化为求每个子串 \(s_i,s_{i+1},s_{i+2},\cdots ,s_{n-i},s_{n-i+1}\) 的最长前缀 \(l\) 满足 \(i + l - 1 \le \frac{n}{2}\) 且 前缀 \(l\) 与 后缀 \(l\) 相等。
设 \(f_i\) 表示每个的答案。发现:\(f_i \le f_{i+1} + 2\)。为什么?
- 考虑 \(f_{i+1}\) 拓展到 \(f_i\),就是 \(f_{i+1}\) 添加头和尾,显然长度最长 \(f_{i+1}+2\)。
- 为什么这是最优的?考虑反证法。
- 画图推一推,发现这样的话 \(f_{i+1}\) 理应更大,矛盾。
然后就做完了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const LL B = 67, mod = 1e9 + 21;
const int MAXN = 1e6 + 3;
int n, nex[MAXN], f[MAXN];
LL bp[MAXN], Hash[MAXN];
string s;
LL Get(int l, int r){
return (Hash[r] - Hash[l - 1] * bp[r - l + 1] % mod + mod) % mod;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> s, s = " " + s;
nex[1] = 0;
for(int i = 2, j = 0; i <= n; i++){
while(j > 0 && s[j + 1] != s[i]) j = nex[j];
j += (s[j + 1] == s[i]), nex[i] = j;
}
int ans = 0;
bp[0] = 1;
for(int i = 1; i <= n; i++) bp[i] = bp[i - 1] * B % mod, Hash[i] = (Hash[i - 1] * B % mod + s[i] - 'a' + 2) % mod;
for(int i = n / 2, j = 0, _i; i >= 1; i--){
f[i] = f[i + 1] + 2, _i = n - i + 1;
while(f[i] > 0){
if(i + f[i] - 1 > n / 2 || Get(i, i + f[i] - 1) != Get(_i - f[i] + 1, _i)) f[i]--;
else break;
}
}
for(int l = nex[n]; l > 0; l = nex[l]){
if(l <= n / 2) ans = max(ans, f[l + 1] + l);
}
cout << ans;
return 0;
}
luogu - P6216 回文匹配
二阶前缀和 板子。
KMP + manacher 转化一下,列出式子,发现是一个二阶前缀和:先前缀和,然后对于前缀和数组再前缀和。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 6e6 + 3;
const LL mod = (1ll << 32);
int n, m, nex[MAXN], d[MAXN];
LL s[MAXN], S[MAXN], ans = 0;
string s1, s2;
LL Get(int l, int r){
if(l > r) return 0;
return (S[r] - S[l - 1]) % mod;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m >> s1 >> s2, s1 = " " + s1, s2 = " " + s2;
nex[1] = 0;
for(int i = 2, j = 0; i <= m; i++){
while(j > 0 && s2[j + 1] != s2[i]) j = nex[j];
j += (s2[j + 1] == s2[i]), nex[i] = j;
}
int mid = m / 2;
for(int i = 1, j = 0; i <= n; i++){
while(j > 0 && s2[j + 1] != s1[i]) j = nex[j];
j += (s2[j + 1] == s1[i]);
s[i] = s[i - 1];
if(j == m){
s[i]++;
}
S[i] = S[i - 1] + s[i];
}
for(int i = 1, l = 0, r = -1; i <= n; i++){
d[i] = (i <= r ? min(r - i + 1, d[l + r - i]) : 1);
while(i + d[i] <= n && i - d[i] > 0 && s1[i + d[i]] == s1[i - d[i]]) d[i]++;
if(r < i + d[i] - 1) l = i - d[i] + 1, r = i + d[i] - 1;
if(i > mid && i <= n - mid && mid <= d[i] - 1){
ans = (ans + Get(i + mid, i + d[i] - 1) - Get(i + m - (d[i] - 1) - 2, i + m - mid - 2) + mod) % mod;
}
}
cout << ans;
return 0;
}
CF1761G - Centroid Guess
参考题解:https://www.luogu.com.cn/article/prukmej0
首先:注意到题面有这样一句话 Hacks are disabled in this problem. 所以正解大概率是随机化。
如果已经知道重心在链 \([x,y]\) 上,我们可以 \(2n\) 次询问求得重心。这种做法感觉比较巧妙:
- 设 \(s_i\) 表示链上第 \(i\) 个节点可以不通过链上的边到达的点的个数。
- 发现只有 \(\max(\sum\limits_{j=1}^{i-1}{s_j}, \sum\limits_{j=i+1}^{n}{s_j}) \le \left\lfloor \frac{n}{2} \right\rfloor\) 的第 \(i\) 个点是重心。因为不满足这个的点都显然不是重心,而满足这个的点只有一个(感觉这一步很妙,省了好多实现)。
- 至于如何计算 \(s_i\),只需要 \(dis(x,p) - dis(y,p)\) 唯一对应即可。
还剩余 \(5 \cdot 10^4\) 次询问。有一种暴力做法,一开始随意选 \(x\),然后 \(x\) 不断走向最大的子树,知道叶子结点 \(y\)。
CF702F - T-Shirts
暴力对每次询问 \(O(n)\) 做一遍,感觉很难优化。考虑反过来。
将 T 恤排序,从右向左扫,每次对询问统一操作。用平衡树维护。
将值域分为 \([1,c),[c,2c),[2c,\inf]\),其中 \([1,c)\) 不变,\([c,2c)\) 直接暴力减法,\([2c,\inf)\) 统一减。这样复杂度是对的,因为 \([c,2c)\) 每次减法都会减半,最多进行 \(\log\) 次。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int MAXN = 2e5 + 3;
struct Tree{
int val, rrr, ans, lz, lzans, lson, rson;
}tr[MAXN];
int rt = 0;
int n, m;
PII A[MAXN];
mt19937 rnd(time(0));
void Down(int x){
int ls = tr[x].lson, rs = tr[x].rson;
tr[ls].val -= tr[x].lz, tr[rs].val -= tr[x].lz, tr[ls].lz += tr[x].lz, tr[rs].lz += tr[x].lz;
tr[ls].ans += tr[x].lzans, tr[rs].ans += tr[x].lzans, tr[ls].lzans += tr[x].lzans, tr[rs].lzans += tr[x].lzans;
tr[x].lz = tr[x].lzans = 0;
}
int Merge(int x, int y){
if(x == 0 || y == 0 || x == y) return x | y;
Down(x), Down(y);
if(tr[x].rrr < tr[y].rrr){
tr[x].rson = Merge(tr[x].rson, y);
return x;
}
tr[y].lson = Merge(x, tr[y].lson);
return y;
}
void Split(int x, int w, int &a, int &b){
if(x == 0){
a = b = 0;
return;
}
Down(x);
if(tr[x].val <= w){
a = x, Split(tr[x].rson, w, tr[x].rson, b);
}else{
b = x, Split(tr[x].lson, w, a, tr[x].lson);
}
}
void Insert(int x){
int a, b; Split(rt, tr[x].val, a, b);
rt = Merge(Merge(a, x), b);
}
void Erase(int x){
int a, b, c;
Split(rt, tr[x].val, a, c);
Split(a, tr[x].val - 1, a, b);
swap(b, x);
b = Merge(tr[b].lson, tr[b].rson);
rt = Merge(Merge(a, b), c);
}
vector<int> vt;
void dfs(int x){
if(x == 0) return;
vt.push_back(x), Down(x);
dfs(tr[x].lson), dfs(tr[x].rson);
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for(int i = 1; i <= n; i++){
cin >> A[i].first >> A[i].second;
}
sort(A + 1, A + 1 + n, [](PII x, PII y){ return x.second == y.second ? x.first < y.first : x.second > y.second; });
cin >> m;
for(int i = 1; i <= m; i++){
tr[i] = {0, rnd() % LL(1e9), 0, 0, 0, 0, 0};
cin >> tr[i].val, Insert(i);
}
for(int i = 1; i <= n; i++){
int C = A[i].first;
int a, b, c;
Split(rt, C - 1, a, b);
Split(b, 2 * C - 1, b, c);
if(c > 0) tr[c].lzans++, tr[c].ans++, tr[c].val -= C, tr[c].lz += C;
vt.clear(), dfs(b);
rt = Merge(a, c);
for(int x : vt){
tr[x].lson = tr[x].rson = 0, tr[x].val -= C, tr[x].ans++, Insert(x);
}
}
vt.clear(), dfs(rt);
for(int i = 1; i <= m; i++) cout << tr[i].ans << " ";
return 0;
}
luogu - P1654 OSU!
有 \((x+1)^3 = x^3 + 3 \cdot x^2 + 3 \cdot x + 1\)。
期望是可以拆分后求和的。算出 \(i\) 为结尾的长度 \(l^2,l\) 的期望值,然后再来算答案。具体见第一篇题解。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e5 + 3;
int n;
double p[MAXN];
double fi[MAXN], se[MAXN], ans[MAXN];
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for(int i = 1; i <= n; i++){
cin >> p[i];
fi[i] = p[i] * (fi[i - 1] + 1);
se[i] = p[i] * (se[i - 1] + 2.0 * fi[i - 1] + 1.0); // (x+1)^2 = x^2 + 2x + 1
ans[i] = ans[i - 1] + p[i] * (3.0 * se[i - 1] + 3.0 * fi[i - 1] + 1.0); // (x+1)^3 = x^3 + 3x^2 + 3x + 1
}
cout << fixed << setprecision(1) << ans[n];
return 0;
}
luogu - P4550 收集邮票
标准的期望dp,逆推 + 推dp方程。
参考题解:https://www.luogu.com.cn/article/4nzvg8pt
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MAXN = 1e4 + 3;
int n;
double f[MAXN], g[MAXN];
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
f[n] = 0;
for(int i = n - 1; i >= 0; i--){
f[i] = f[i + 1] + double(n) / double(n - i);
}
g[n] = 0;
for(int i = n - 1; i >= 0; i--){
g[i] = f[i] * i / double(n - i) + g[i + 1] + f[i + 1] + double(n) / double(n - i);
}
cout << fixed << setprecision(2) << g[0];
return 0;
}
UVA10288 - 优惠券 Coupons
这题可以和 P4550 收集邮票的第一步一样 dp 方程做。但是还可以推等比数列来做。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using PLL = pair<LL, LL>;
void doit(PLL &x){
LL G;
while((G = __gcd(x.first, x.second)) > 1){
x.first /= G, x.second /= G;
}
}
int getbit(LL w){
int c = 0;
while(w > 0) w /= 10, c++;
return c;
}
void puts0(int c){
while(c--) cout << " ";
}
void puts_(int c){
while(c--) cout << "-";
}
PLL ADD(PLL x, PLL y){
doit(x), doit(y);
PLL ret = {x.first * y.second + x.second * y.first, x.second * y.second};
doit(ret);
return ret;
}
int main(){
int n;
while(cin >> n){
PLL ans = {1, 1};
for(int a = 1; a < n; a++){
ans = ADD(ans, PLL({a, n - a}));
ans = ADD(ans, PLL({1, 1}));
}
doit(ans);
if(ans.second == 1){
cout << ans.first << "\n";
continue;
}
LL _ans = ans.first / ans.second;
ans.first %= ans.second;
puts0(getbit(_ans) + 1); cout << ans.first << "\n";
cout << _ans << " "; puts_(getbit(ans.second)); cout << "\n";
puts0(getbit(_ans) + 1); cout << ans.second << "\n";
}
return 0;
}
luogu - P1039 [NOIP2003 提高组] 侦探推理
简单枚举 + 简单模拟 + 分类讨论
思考时间 5min,预期实现时间 20min,实际实现时间 1h。
使用 getline 的时候出问题了,看题解才知道 Linux 和 Windos 不同环境读入不太一样,直接 if(ch=='\n'||ch=='\r'||ch==' ') s.pop_back() 就好了。
小看这题了,思考时漏有两种情况:
- 所有人都不是罪犯,那么剩下的那个人就是罪犯。
- 没人确定犯罪,且多人不确定状态,则多解
luogu - P8439 Altale (Fan-made FTR 7)
基环树 + 反悔贪心
思考时间 30min,看题解了,预期实现 30min,实际实现 1.5h。
个人感觉基环树有两种思考角度:
- 环上长出一些子树
- 一棵树上添加了一条边
最近碰到的基环树题都是用的第一种角度,这题我用第一种角度没想出来,看了题解才发现可以用第二种角度。或许有根树更适合用第二种。
转化后是标准的反悔贪心,这题反悔贪心的弱化版本:https://www.luogu.com.cn/problem/CF436E
注意反悔贪心的时候 \(i,j\) 也有顺序要求,不能乱用。注意需要及时 pop 选择了的状态。注意 vis 数组的类型,尽量直接使用 int。
CF1930H - Interactive Mex Tree
关于 mex 的 trick + dfs序 + 分类讨论 + 构造
思考时间 10min,看题解了,预期实现 10min,实际实现 30min。
trick:对于一个全排列(\(0\) 到 \(n-1\) 且互不相同),求一个集合的 mex,实际就是求不在集合中的元素的最小值。
问题变为求树上:不在两点之间的元素的最小值。注意这题需要所有询问开始前构造出两个排列(我一开始没注意到这个……)。
关于 dfs 序:入栈序dfn、出栈序dfe、欧拉序。
分 \(u\) 和 \(v\) 是先祖关系 以及 \(u\) 和 \(v\) 不是先祖关系 讨论。这题只需要用到入栈序和出栈序,具体讨论见题解 https://www.luogu.com.cn/article/3bmvr2ku 。 因为 \(nq \le 3 \cdot 10^6\),所以暴力求 LCA 就可以了。
这题傻逼吗?它在处理完一次询问后还要输入一个值表示你的答案是否正确。我没有读入这个,一直 WA 3,卡了 20min,红温了。
luogu - P3615 如厕计划 & [AT_joisc2016_f]トイレ
普通贪心 + 后缀和
思考时间 1h(大部分时间是被读错题占了),看题解了,预期实现时间 10min,实际实现时间 10min。
被气笑了,洛谷屎题面,读漏(错)四个地方:
- 恰好 2N 个学生
- 答案是取最大值 不是 取总和。
- 这题不是只能交换两个人,本质是将一个人抽离,再插入到某个位置。
- 这题给出的队列是从尾到头的,下面考虑从头到尾的。
先特判妹子个数少于一半,直接 -1。
\(2n\) 个人在 \(n\) 分钟内全部完成,也就是每时刻两个厕所都有人。先思考 check ,显然是不能让太多妹子集中在左侧,考虑后缀和。男权值 \(-1\),女权值 \(1\)。一个排列合法,也就是每个位置的后缀和都大于 \(-2\)。
然后我不会了,因为我是在考虑妹子如何向右移,而题解是考虑男生如何向左移动。
向左移动的答案始终为 \(0\),所以男生一定是移到最左侧,这会使得一个前缀内的所有妹子的答案加一,并且一个后缀的所有后缀和加一。所以只需要计算原序列的最小后缀和即可。
luogu - P11268 【MX-S5-T2】买东西题
反悔贪心
思考时间 30min,预期实现时间 10min,实际实现时间 10min。
考虑贪心,发现可以将 \(a\) 升序,\(w\) 升序,依次枚举 \(a_i\),双指针得到可以降价的所有 \(v\)。显然这个集合是不断增大的(也就是所有集合之间是包含关系)
想了一会发现普通贪心无法解决,发现可反悔贪心。
luogu - P11212 『STA - R8』挑战 Goldbach 猜想
质数
思考时间 5min,预期实现时间 5min,实际实现时间 5min。
印象中 \(n\) 以内的质数个数大概是 \(\frac{n}{\log n}\) 量级的。考虑答案预处理,就按代码那样执行:
for(int i = 0; i < pr.size(); i++){
for(int j = 0; j < i; j++){
for(int w = pr[i]; w <= V; w += pr[i]){
ans[w + pr[j]]++;
}
}
}
\(V = 2e5,l=\sum\limits_{p\in Prime}{[p \le V]} = 17,984\),复杂度为 \(\sum\limits_{i=0}^{l-1}{\frac{V}{pr_i} \cdot i} = 305,760,487\)
luogu - P11159 【MX-X6-T5】再生
组合数学
思考时间 30min,预期实现时间 5min,实际实现时间 5min。
实际就是给了一些链,要求从长到短依次添加到树上,求最后方案数。推推样例就玩出来了。
UVA1435 - Business Cards
CF1981E - Turtle and Intersected Segments
优化建图 + 生成树
思考时间 1h,看题解了,预期实现时间 20min,实际实现时间 15min。
现在看到这种边多的最小生成树题直接就想 Boruvka 去了,想出一个很复杂难写的思路,试着想其他思路,但没想出来,就看题解了,没想到优化建图(也就是省去最小生成树中一定不选的边)。
考虑 kruskal 的过程。按照边权排序然后依次加入,所以:如果存在一个环,那么环中边权最大的那条边一定不选(因为在选之前两端点保证已经合并了)。
考虑扫描线,到 \(l_i\) 就插入 \(i\),到 \(r_i + 1\) 就删除 \(i\),那么在每个位置都有一个集合 \(S\),显然集合中任意两点之间都有边。考虑连边,普通的连接方式:在插入一个点时,\(i\) 与当前集合 \(S\) 中每个点都连一条边。
根据性质,只需要连接满足 \(a_j\) 是 \(a_i\) 前驱或后继的 \(j\)。
CF1994G - Minecraft
动态规划 + 进位
思考 30min,看题解了,预期实现 20min,实际实现 15min。
WA 了一发,因为是脑残把下标写错了。
我的想法:先暴力计算得到可以得到的最小值,问题变为类似背包的问题(只是至于很大),从低位到高位依次确定,但是每一位可以添加的值最多影响到向前 \(\log n\) 位,所以只用背一个 \(n\) 以内的数,最后得到一个 \(O(nk)\) 的做法。
看了眼题解,原来我那个几个转化是多余的,即没有必要转化为背包问题。发现最多影响向前 \(\log n\) 位就可以直接做了。
每一位当前值的最大是 \(\sum_{l=0}^{\log n}{\frac{n}{2^l}}\),对于 \(\sum_{l=1}^{\log n}{\frac{n}{2^l}}\) 是调和级数永远小于 \(n\),所以最大值小于 \(2n\)。
CF1175E - Minimal Segment Cover
前綴max + 倍增
思考时间 30min,预期实现时间 10min,实际实现时间 10min。
trick:通过取前缀 max 来得到每个点可以到达的最远点。
这个扇贝 trick 我尽然想了这么久……
然后就是普通倍增了。
CF1792E - Divisors and Table
约数 + 复杂度分析
思考时间 30min,预期实现时间 15min,实际实现时间 15min。
可以根据 \(m1,m2\) 得出 \(m\) 的所有约数。
对每个约数 \(w\),得到最小 \(x\) 满足 \(\frac{w}{x} \le n\),然后在约数序列中二分得到一个值,然后向上枚举,直到找到合法的。
感觉这种方法可以过,然后没想到就 AC 了。不会复杂度分析。
CF209C - Trails and Glades
欧拉回路(无向图)+ 分类讨论
思考时间 10min,预期实现时间 15min,实际实现时间 15min。
复习一下:无向图欧拉回路存在,当且仅当每点度数为偶数。
对于一个联通块是简单的,但是如何考虑多个联通块?为了使边最少,一定是联通块之间连成一个环。
分情况讨论(一个联通块、多个联通块),比较简单。
WA 了一发,因为对欧拉回路的定义不熟悉:从一个点出发,把每条边都经过恰好一遍。所以单独的节点是不能管的。
CF919E - Congruence Equation
同余 + 推式子
思考时间 30min,看题解了,预期实现时间 10min,实际实现时间 5min。
注意 \(p\) 为质数,\(n a^n \equiv b \pmod{p}\) 中系数 \(n\) 的循环节是 \(p\),指数 \(n\) 的循环节是 \((p-1)\)。
然后不会了,看题解,才明白这时候需要设 \(n = k (p - 1) + r(0 \le r < p - 1)\)。
带入,推出 \((r - k) \equiv b a^{-r} \pmod{p}\)。
因为 \(r < p-1\),所以可以枚举 \(r\)。然后得出 \(k \bmod p\) 的值,此时 \(n\) 的循环节是 \(p(p-1)\),统计合法答案即可:得出最小 \(n\),然后根据循环节得出数量。
CF715B - Complete The Graph
最短路
思考时间 20min,看题解了,预期实现时间 20min,实际实现时间 30min。
各种奇怪做法都没想出来,然后就看题解了。感觉法一和法二都非常妙~~~~
法一:
考虑关于边权的复杂度,即直接搜索,考虑优化。对零边定义编号 \(1,2,3,\cdots,e\)(初始所有权值为 \(1\)),然后依次 \(val_1++,val_2++,val_3++,\cdots,val_e++,val_1++,val_2++\cdots\),知道最短路等于 \(L\)。考虑正确性:
- 当然是需要证明每 \(++\) 一次,最短路最多增加 \(1\)。
- 这个是显然的,毕竟边权都是每次最多增加 \(1\)。
考虑优化,即二分操作次数,然后 check。
法二:
直接最短路不行,就添加状态:\(dp_{i,j}\) 表示到达 \(i\) 点恰好经过 \(j\) 条零边的最短路(零边边权为 \(0\))。
对于 \(dp_{t,j}\),找到最小的 \(j\) 满足 \(dp_{t,j} + j \le L\),那么把这 \(j\) 条零边附合适的权值,其余都附极大值。考虑正确性:
- 考虑反证法。如果不正确,当且仅当存在另外一条最短路,只经过了 \(j-1\) 或更少条零边。
- 但是我们是找到最小的 \(j\),矛盾。
实现中的错误:我用的法一。
- 第一发WA因为我直接用 check 来判断答案是否合法,但是是需要判 \(dp_T\) 等于 \(L\)。
- 第二法TLE,查了很久,最后发现是
priority_queue我直接用的,没有改为小根堆(傻逼错误)。
luogu - P2233 [HNOI2002] 公交车路线
矩阵乘法
思考 1min,预期实现 5min,实际实现 15min。
矩阵乘法优化板子。
傻逼了,由于中途是不能到达 E,所以我直接封死 E 的所有转移,导致答案始终为 0,需要 \(n--\) 然后统一 D 和 F 的方案数(在这卡了一会)。
luogu - P4159 [SCOI2009] 迷路
矩阵乘法 + 优化建图
思考 5min,预期实现 10min,实际实现 20min。
拆点,然后板子矩阵乘法优化。
建矩阵的时候建反了,多调了一会。主要是没怎么写过矩阵乘法。
luogu - P2151 [SDOI2009] HH去散步
优化建图 + 矩阵乘法
思考时间 10min,看题解了,预期实现时间 15min,实际实现时间 15min。
完全忘记如何处理不能连续走同一条边,改如何处理,就看题解了。
trick: 点边互换。
还需要将边拆为两条有向边。
luogu - P6406 [COCI2014-2015#2] Norma
cdq 分治 + 分类讨论
思考时间 30min,预期实现时间 30min,实际实现时间 30min。
哥几个又来练分讨了。
一眼 CDQ 分治。考虑大力分讨。
把式子拆开是 \((r + 1) \times\)min\(\times\)max \(- l \times\)min\(\times\)max,然后分类 max 在左侧还是右侧、min 在左侧还是右侧,去讨论即可。
注意这题需要取模。
luogu - P10871 [COTS 2022] 皇后 Kraljice
构造
思考时间 20min,看题解了,预期实现时间 20min,实际实现时间 20min。
猜 \(n\) 为奇数时答案是 \(n^2\),然后完全不会了……
构造思路:如何不断使得 \(n\) 变小?
可以把边框填上皇后,内部所有格子也恰好被 \(8\) 个边框上的皇后攻击,不被影响,也就直接变为了 \(n-2\) 的子问题。
填边框需要分奇数偶数讨论(这个过程构造有些困难,也不知道有什么可以总结的,完全凭感觉?),具体构造方法看题解 https://www.luogu.com.cn/article/o5g02a2k 。
在减少到 \(n=3,4\) 的时候,就直接手推或暴搜。所以需要提前特判一下 \(n \le 2\)。
[ARC179E] Rectangle Concatenation
动态规划 + 扫描线
思考时间 20min,看题解了,预期实现时间 20min,实际实现时间 10min。
不会,就看题解了。
先要注意到面积无论如何操作都不变。
先确定 \(l\),然后 dp。得到了 \(O(n^2)\) 的做法。具体转移式看 https://www.luogu.com.cn/article/zutxkiet 里的。
从小到大枚举 \(r\),对 \(f_{i,0}\) 和 \(f_{i,1}\) 都维护所有可以的 \(l\)。发现从 \(r\) 到 \(r+1\),变动都是 \(O(1)\) 级别的,然后直接做就可以了。
[ARC084F] XorShift
线性基
思考时间 10min,看题解了,预期实现时间 30min,实际实现时间 20min。
讲评的题目。
比较显然:先把所有数乘 \(2^x\) 的结果写上,再相互异或。
\(x\) 太大并没有意义,发现 \(x\) 最多 \(4000\) 就足够了。
考虑线性基,发现需要插入 \(n \times 4000\) 个位数 \(8000\)(为了方便,就当作是 \(4000\) 吧) 的数,复杂度 \(O(n \times 4000 ^3)\)。即便 bitset 优化也过不了。
发现:插入一个数 \(S\),得到 \(T\),再来插入一个 \(S \times 2\) 等价于插入一个 \(T \times 2\)。
分析复杂度:一个数会不断最高位下滑一位,而每次乘二,只会最高位上升一位,所以插入一个数的复杂度是 \(O(4000^2)\) 的。
只有 \(n\) 个数需要插入,复杂度 \(O(n 4000^2)\)。可用 bitset 优化。
接下来就是一个板的数位 dp。
luogu - P5307 [COCI2018-2019#6] Mobitel
整除分块 + 动态规划
思考时间 40min,预期实现时间 20min,实际实现时间 20min。
不小心看到标签上有分块,一开始以为是把 \(n\) 分开,想了一些做法都不对,感觉不是普通的分块。
状态第三维无法避免。不如转化为至少还需要乘多大的数,积才可以大于等于 \(n\)。转移就是 \(k\) 转移到 \(\left\lceil\dfrac{k}{d}\right\rceil\)。
整除分块,总结。
引理1(向上取整也任然成立)说明所有可能的 \(k\) 都是 \(\left\lceil\dfrac{n}{x}\right\rceil\)。引理2 说明最多只有 \(O(\sqrt{n})\) 种 \(k\)。
最后复杂度 \(O(rc\sqrt{n})\)。
WA 了一发,因为没有注意到数量是 \(2 \sqrt{n}\),所以第三维需要开 \(2 \cdot 10^3\)。
[AGC008D] K-th K
贪心
思考时间 30min,预期实现时间 10min,实际实现时间 10min。
一个限制可以拆分为两个限制:
- \(i\) 必须在 \([1,x_i-1]\) 中出现 \(i-1\) 次。
- \(i\) 必须在 \([x_i+1,n^2]\) 种出现 \(n-i\) 次。
前扫一遍,后扫一遍,就没了。
CF645E - Intellectual Inquiry
动态规划 + 走路题
思考时间 1h,预期实现时间 20min,实际实现时间 20min。
走路题,第一步显然是想:如何统计不同子序列数量。
- 考虑 dp。设 \(f_{i}\) 表示前 \(i\) 个字符有多少不同子序列。如果直接 \(f_i = 2 \times f_{i-1}\),会算重复,考虑哪里会算重复?
- 当前字符是 \(c\),则前面所有以 \(c\) 结尾的的子序列都会重算一遍。
- 设 \(g_{c}\) 表示字符 \(c\) 结尾的不同子序列数量。设当前字符是 \(c\),则 \(g_c = \sum\limits_{i=0}^{k-1}{g_c}\)。
- 但是这个转移式子忽略了空串的情况,所以应该是添加 \(g_k\) 表示空串结尾的数量。
- \(g_k\) 初始值设为 \(1\),然后 \(g_c = \sum\limits_{i=0}^{k}{g_c}\)(\(c\) 不能等于 \(k\)) 推下去就可以了。
观察这个转移,如果可以选则 \(c\),则每次选最小的 \(g_c\) 去转移最优。
还发现每经过一次转移 \(g_c\) 又会变为最大值。
然后就可以直接做了。
考虑离散化,每次转移 \(g_c\),只需要把 \(g_c\) 的离散值设为当前离散值中最大的就可以了。
WA 了两发,都是因为数组开小了。
[AGC002E] Candy Piles
图论建模 + 博弈论
思考时间 1h,看题解了,预期实现时间 10min,实际实现时间 10min。
可以先把 \(a\) 排序,第一个操作就是删除最后面的值,第二个操作就是全局减一。然后不会了,就去看题解了。
trick:序列也可以画平面图。
得到这样一个图(横坐标是位置,纵坐标是值):
....#
...##
.####
#####
问题转化为:起点是右下角,一操作是向左移动,二操作是向上移动,走到界外或 . 的人输。
我手玩的时候出了个问题,白白卡了好久(感觉博弈论好烧脑):
- 所有边缘上的
#都不一定是后手必胜。我没注意到这个……
然后手玩一下发现所有在一条斜线上的状态相等。找到最大正方形,也就是把求正方形右下角的状态转为求正方形左上角的状态,而左上角是贴边的,可以直接求出。
luogu - P7595 「EZEC-8」猜树
根号分治
思考时间 30h,预期实现时间 20min,实际实现时间 20min。
想了各种奇奇怪怪的做法,然后尽然想出来了。
显然可以通过 \(n\) 个数得出每个点的深度。考虑相邻两层如何确定父子关系。
如果全部用 1 操作,花费 \(cnt_i \times cnt_{i+1}\) 个数。
如果全部用 2 操作,花费 \(\sum\limits_{x\in S_i}{sz_{x}}\) 个数。
考虑根号分治。对于 \(cnt \le \sqrt{n}\),就第一种做法,否则第二种做法。复杂度比较显然。
CF1237E - Balanced Binary Search Trees
构造
思考时间 30min,看题解了,预期实现时间 5min,实际实现时间 5min。
初步有一些简单的发现,我都想出来了,但是最后那个发现我没想出来。
一个很厉害的发现(可以归纳法证明):
- 需要证明深度为 \(i(i \ge 3)\) 的合法的数的大小值有且只有可能 \(f_i\) 或 \(f_i+1\)
写的 题解。
luogu - P2512 [HAOI2008] 糖果传递 & luogu - P2125 图书馆书架上的书
推式子 + 贪心
思考时间 30min,看题解了,预期实现时间 10min,实际实现时间 10min。
这题标贪心可以认为是纯诈骗。我一直在盲目思考贪心,但是这题实际是要设未知数然后去推。
设 \(X_i\) 表示 \(i\) 要向左传多少糖果(可以为负)。具体推式子去看 https://www.luogu.com.cn/article/g9wlldda 里的。
最后得到 \(X_i = X_1 - C_i\)。而问题是最小化 \(\sum\limits_{i=1}^{n}{|X_i|}\),也就是最小化 \(\sum\limits_{i=1}^{n}{|X_1 - C_i|}\)。
这是很标准的贪心问题,\(X_1\) 取中位数(注意不是平均数)即可。
luogu - P4198 楼房重建
兔队线段树
思考时间 10min,看题解了,预期实现时间 20min,实际实现时间 20min。
兔队线段树模板题。https://www.luogu.com/article/ka3ywxlj
CF895C - Square Subsets
线性基
思考时间 10min,看题解了,预期实现时间 10min,实际实现时间 10min。
一个数质因数分解后,可以每个质因数指数取模 \(2\),变为一个 01 串,一个子集乘积为完全平方数,也就是所有 01 串异或起来等于 \(0\)。
线性基如何解决此问题?数多少子集满足异或和为 \(0\)。
考虑一些元素会插入线性基,有一些不会。设插入线性基有 \(x\) 个,那么没插入的有 \(n-x\) 个。
在没插入的元素的集合中,选择一个子集 \(T\)。显然 \(T\) 中所有元素都可以被线性基唯一表示出来,那么异或和也可以被线性基唯一表示出来。
所以答案为 \(2^{n - x}\)。但是这题要求集合非空,答案 \(2^{n - x} - 1\)。
luogu - P7451 [THUSCH2017] 杜老师
分块 + 线性基
思考时间 10min,看题解了,预期实现时间 20min,实际实现时间 30min。
讲评的题目。
这就是 CF895C - Square Subsets 的加强版。
接下来考虑暴力优化复杂度:根号分治。
小于 \(\sqrt{R}\) 的质数最多 453 个,而大于 \(\sqrt{R}\) 的质数在每个数中最多出现一次。复杂度优化为 \(O(\frac{(R-L+1) \times 453^2}{w})\)。
玄学优化:若 \(R-L+1\) 很大(大概是 \(2\sqrt{R}\)),发现线性基一定被填满。注意我们只需要 \(x\) 的取值,那么只需要统计 \([L,R]\) 中的质因数个数。
第一发 MLE,因为我直接把 \([1,10^7]\) 的质因数全部存下来了。
第二法 WA,没注意到线性基某个位置有可能为空,不能直接 a[bit].none() 判,需要新建一个标记数组。
CF1097F - Alex and a TV Show
推式子 + bitset
思考时间 30min,看题解了,预期实现时间 20min,实际实现时间 。
如果没 3 操作就是 bitset 板子了,然后想了各种做法都和题解沾不上边。
看到 \(\gcd\) 就应该想到退式子或反演,这个坑已经在 [ARC185E] Adjacent GCD 踩过一次了。
为了反演,考虑改维护每个约数的出现次数。如果操作 2 就是两个集合 ^,如果操作 3 就是两个集合 &(因为就是每一位相乘,10=0,11=1,00=0)。
考虑反演。设原可重集为 \(A\),约数可重集为 \(B\)。答案为 \(\sum\limits_{x\in A}{[x=v]} = \sum\limits_{x\in A}{[\frac{x}{v}=1]} = \sum\limits_{x\in A}{\sum\limits_{p|\frac{x}{v}}{\mu(p)}} = \sum\limits_{d\in B, v | d}{\mu(\frac{d}{v})}\)。
luogu - P8392 [BalticOI 2022 Day1] Uplifting Excursion
CF1111E - Tree
动态规划
思考时间 30min,看题解了,预期实现时间 30min,实际实现时间 30min。
对每次询问,可以根据到根的距离来分层,然后考虑 dp。
我一直在思考自下而上的 dp,由于子树内分出的集合数量不一定,所以复杂度带一个 \(m^2\),做不了,感觉自己被骗了,就去看题解了。
转换一下思考,考虑自上而下 dp,设 \(v_i\) 表示 \(i\) 的祖先的个数,那么所有祖先一定是分为 \(v_i\) 个集合,容易得到转移式子 \(f_{i,j} = f_{i-1,j-1} + f_{i-1,j} \times (j - v_i)\)。
至于 \(v_i\) 需要 树链剖分 + 树状数组 求。
太久没写树链剖分了,有些细节没注意:
- 求 LCA 判断是
if(dep[top[x]] > dep[top[y]]) swap(x, y); - 求 LCA 的终止条件是
while(top[x] != top[y]){ - 达到
top[x] = top[y]时还需要统计x,y之间的贡献。
luogu - P2757 [国家集训队] 等差子序列
字符串哈希 + 树状数组
思考时间 30min,看题解了,预期实现时间 20min,实际实现时间 20min。
一直在盲目思考,脑子也没有及时去转换,一直在思考把 \(i\) 染色,但是实际上需要对值域染色。
考虑从左往右扫,扫到一个 \(a_i\),就把 \(a_i\) 位置染 \(1\)(初始全部为 \(0\))。
如果存在一个 \(j\) 满足 \(c_{a_i-j} \ne c_{a_i+j}\),就说明存在一个长度 \(3\) 的等差数列。
问题也就是判断是否为回文串,变为 [ABC331F] Palindrome Query。
其
求左边第二个小于自己的:
https://www.luogu.com.cn/article/ssfdnurm

luogu - P3899 [湖南集训] 更为厉害
做法很显然,但是如果直接 \(i\) 这个节点的 01-Trie 需要把所有儿子的 01-Trie 都合并,有点麻烦。
可以按照 dfn 来依次合并。
luogu - P6047 丝之割
用和 https://www.cnblogs.com/huangqixuan/p/18446558#luogu---p5896-ioi2016-aliens 一样的 trick
对于 \(u_1 \ge u_2\) 且 \(v_2 \ge v_1\) 则把 \(1\) 删除。
剩余的所有弦,满足 \(u\) 越大 \(v\) 越大。
把弦按照 \(u\) 从小到大。\(f_i\) 表示把前 \(i\) 个剪短的最小代价。有 \(f_i = \min(f_j + (\min\limits_{x=v_i+1}^{n}{b_x}) \times (\min\limits_{x=1}^{u_{j+1} - 1}{a_x}))\)
考虑斜率优化,对标 b = y - k * x。这里把 \((-\min\limits_{x=1}^{u_{j+1} - 1}{a_x},f_j)\) 看作 \((x,y)\),那么 \(k=\min\limits_{x=v_i+1}^{n}{b_x},b=f_i\)。
显然 \(k\) 递增,\(y\) 递增,\(x\) 递增。直接做就行了。
注意:求两点斜率时,需要特判 \(x_1=x_2\)。
CF1458D - Flip and Reverse
把 0 看作 \(-1\),1 看作 \(1\),得到前缀和数组。
一次操作就是找到一个 \(s_{l-1}=s_r\),然后对 \(s[l,r]\) 操作:
- 为了方便理解,把 \(s[l,r]\) 全部减 \(s_{l-1}\) 得到前缀数组 \(b[1,n]\)。
- 先全部取反就是 \(b_i = -b_i\)。
- 再翻转:有 \(b_n = s_r - s_{l-1} = 0\),所以 \(b_i = b_n - b_{n - i} = -b_{n-i}\)。
- 两个步骤合并实际就是 \(b_i = b_{n-i}\)。
- 所以一次操作就是把 \(s[l,r-1]\) 翻转。
最后要 01 串字典序最小,可以转为要 \(s\) 前缀和数组字典序最小。
可以每次 \(s_i\) 到 \(s_{i+1}\) 连接一条有向边(注意 \(s_0\) 到 \(s_1\) 也需要连)。没任何操作的话,会有一个固定的路径。
注意到可以随意调整走向儿子的顺序(回到 \(s\) 数组上,例如 x...x...x,可以先把 ...x... 翻转,再把两个 ... 翻转,等价于调整了走向儿子的顺序)。
现在问题变为:每次可以把一个环上所有边的方向反过来,求最后字典序最小的欧拉回路。
注意到对某个环的一次操作,不会改变有向边集合(因为这题的所有环都是类似 \(1 \to 2 \to 3 \to 2 \to 1\) 的,反向后显然没有改变边集)。
所以这个操作无论怎么操作都不会改变答案,直接忽略即可。
关于实现:如果你想装逼不写 dfs,想写循环,就需要注意判断存在 \(x \to (x-1)\) 还需要判断存在 \((x-1) \to x\)。
luogu - P4755 Beautiful Pair
(这题我是来练笛卡尔树的)
先建出大根笛卡尔树。众所周知区间最大值就是两个点 LCA 的值。
需要启发式合并。
[AT_cf17_final_j] Tree MST (太懒惰了,还没写)
参考题解:https://www.luogu.com.cn/article/k9dpcm1x
求完全图最小生成树,考虑 Boruvka。
问题是要找到不与 \(p\) 在同一联通块且距离 \(p\) 最近的距离。
如果每个联通块大小为一,容易树形 dp 求出。
可以额外记录次小值,满足次小值和最小值所在联通块不同。
参考题解:https://www.luogu.com.cn/article/qyeh1m07 (点分治做法)
对于一个边集求 MST,选择一个子集,对这个子集求 MST,没留下来的边可以从原边集中删除,不影响答案。
考虑点分治,求出跨越分治中心的边集的 MST,保留这些边,最后再一次 MST。
[ABC213G] Connectivity 2
可以求出每个子图的方案数,然后统计答案,比较简单。
困难的是求每个子图的方案数。
对于一个子图,考虑容斥。初始等于所有方案数,减去不合法的方案数。随意选择一个点,然后枚举不合法方案中那个子集包含了这个点,然后计算机算。
不太想讲了,不如看代码。实际这题没多难,主要是需要走写步骤,够自信才能做出来。
luogu - P5972 [PA2019] Desant
模拟赛考题。
\(O(2^n)\) 做法很显然,状态数太多了,mid in middle 也不行,考虑减少状态。
假设为对于 \(1,\cdots,i\) 的子集都已经计算完了,加下来转移,只需要保留 \([1,x_{i+1}),(x_{i+1},x_{i+2}),\cdots,(x_n,n]\) 这些区间中出现次数。
每个位置接下来的状态数是 \(\prod{L_i}\),每个位置最大状态是是平均分配,所以最大 \((\frac{n}{n-i+1})^{n-i}\)。那么总状态数是 \(\sum\limits_{i=1}^{n}{(\frac{n}{n-i+1})^{n-i}}\),\(n=40\) 时大概是 \(2 \cdot 10^7\) 大小。
复杂度 \(O(n\sum\limits_{i=1}^{n}{(\frac{n}{n-i+1})^{n-i}} \times 一些根据实现的东西)\)。可以使用哈希表,那复杂度 \(O(n^2 \sum\limits_{i=1}^{n}{(\frac{n}{n-i+1})^{n-i}})\)。
luogu - P7118 Galgame
简化题意可以去看:Link
先把 \(\sum\limits_{i=1}^{n-1}{Catalan(i)}\) 算了。
考虑 dfs,到达一个点会有系数,然后需要枚举这个点的左子树大小,可这是 \(O(n^2)\) 的。
可以使用启发式合并+容斥。
luogu - P2617 Dynamic Rankings
讲个笑话:主席树板子的带修加强板子可以不用主席树。
先离散化了。
考虑 \([1,n]\) 每个位置都建一棵值域线段树,记录 \([i - lowbit(i) + 1, i]\) 中所有元素的动态开点值域线段树。
处理查询时整体二分,到一个区间时会有多个点同时存在,有 \(O(\log n)\) 个点。
修改是简单的。
luogu - P3578 [POI2014] LAM-Solar lamps
计算几何显然是不能做的,需要变换坐标系。
看作题目给了两个向量,每个点可以被两个向量唯一表示,对应新坐标 \((a_i,b_i)\),有 \(a_i(x_1,y_1) + b_i(x_2,y_2) = (x_i,y_i)\)。
\(a x_1 + b x_2 = x_i\) 和 \(a y_1 + b y_2 = y_i\),解得 \(a = \frac{y_i x_2 - x_i y_2}{y_1 x_2 - x_1 y_2},b=\frac{x_i y_1 - y_i x_1}{y_1 x_2 - x_1y_2}\)。(\(x_1y_2 - y_1 x_2=0\) 就意味着斜率相同,但题目保证了夹角小于 \(180\) 所以不存在分母为 \(0\))
显然如果一个点在另外一个点的范围内,也就是 \(a_i \le a_j\) 且 \(b_i \le b_j\)。变为网格图上的问题。
考虑整体二分。\(S(l,r,S)\) 表示集合 \(S\) 内的点都满足答案在 \([l,r]\) 中。接下来需要解决的问题是得到 \(S\) 中哪些答案在 \([l,mid]\) 中。
时刻小于等于 \(mid\) 的先加入 \(T\)。对于其他的点做法类似二维数点。
CF1109F - Sasha and Algorithm of Silence's Sounds
判断是否是树,只需要判断无环且联通。
无环是有单调性的,对每个 \(i\) 求出最大 \(z_i\) 满足 \([i,z_i]\) 无环。
假设已知 \(z_i\),如何求 \([i,z_i]\) 中多少 \(j\) 满足 \([i,j]\) 联通?
- 既然已经无环了,判联通转为判是否 \(点数 - 边数 = 1\)。
- 从小到大枚举 \(i\)。维护一颗线段树,每个位置 \(j\) 的权值就是 \([i,j]\) 的 \(点数 - 边数\),每个节点维护最小值和最小值出现次数。
- 查询就是查询 \([i,z_i]\),问题是每次 \(i\) 加一如何修改线段树,这是简单的,不解释了。
如何求 \(z_i\)?
- 显然有单调性 \(z_i \le z_{i+1}\)。
- 如果双指针,发现很难支持删除,可以考虑撤销,不过这和线段树分治也没啥关系啊?考虑整体二分。
- \(S(l,r,L,R)\) 表示 \(z_L,z_{L+1},\cdots,z_R\) 都在 \([l,r]\) 内。
- 需要找到一个 \(pos\) 满足 \(z_L,z_{L+1},\cdots,z_{pos}\) 都在 \([l,mid]\) 内且 \(z_{pos+1},z_{pos+2},\cdots,z_{R}\) 都在 \([mid + 1,r]\) 内:
- 转为求最小的 \(p\) 满足 \([p,mid+1],[p+1,mid+1],\cdots,[R,mid+1]\) 这几个区间组成的图都无环。
- 把 \([R+1,mid+1]\) 并查集建出来,并判断是否有环。
- 然后从 \(p=R\) 开始不断减。
- 可是如何把 \([R+1,mid+1]\) 并查集建出来呢?需要在上一层递归下来的时候做一些处理。
- 递归下去。
- 把并查集撤销到 \([R+1,l-1]\) 的时候。
- 递归到 \(S(l,mid,L,pos)\),把并查集并到 \([pos+1,l-1]\),然后撤销
- 递归到 \(S(mid+1,r,pos+1,R)\),把并查集并到 \([R+1,mid]\),然后撤销
luogu - P11436 [Code+#8 决赛] 生成树
https://www.luogu.com.cn/paste/e322krt4 模拟赛的题。
接下来是模拟赛的做法。模拟赛的做法,在这题不能通过。
神笔构造。
看到可以有重边,如果对 \(k\) 质因数分解,建出一条链。这样做,显然会被 \(k\) 为大质数。
考虑二进制。考虑一个图:
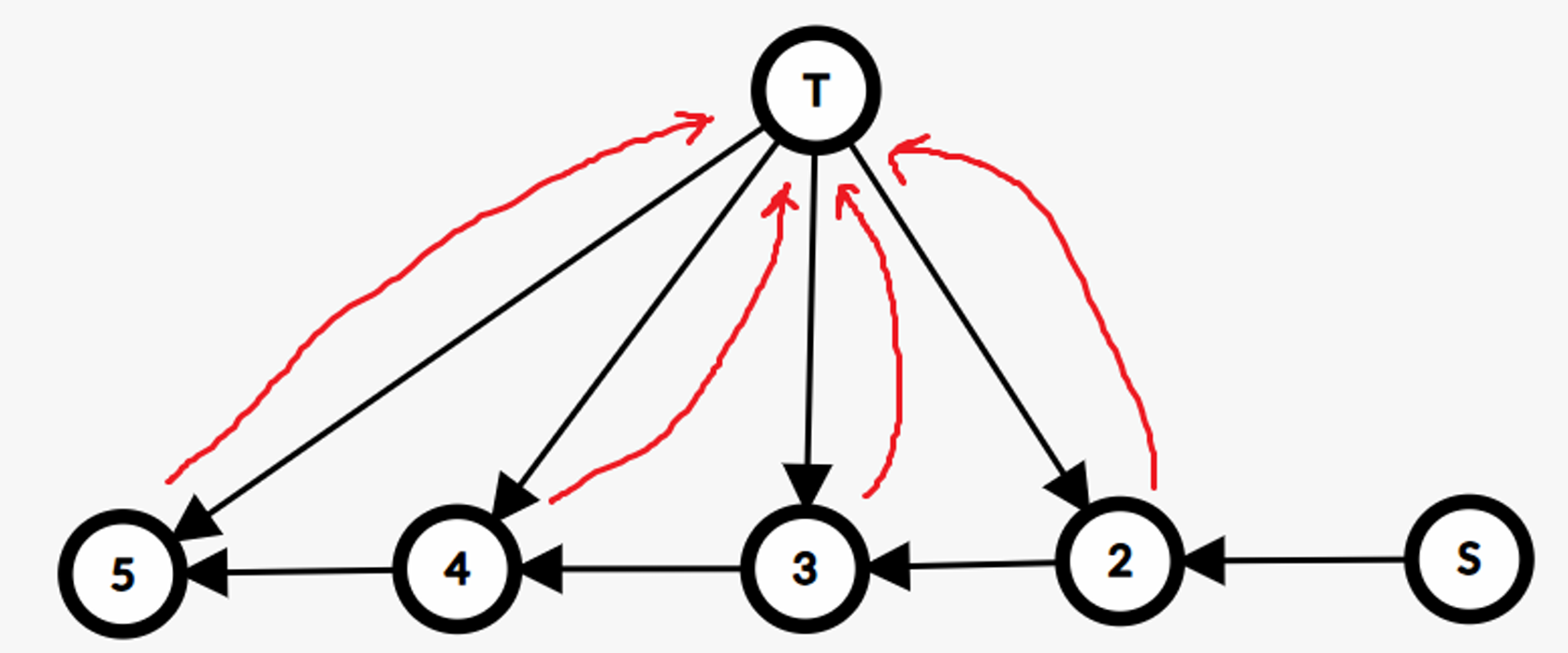
初始没有那些红边,添加从左到右第 \(k\) 条红边,可以使得答案加等于 \(2^{k-1}\),然后就做完了。
为什么?1.有向生成树不会包含两条红边,所以是相加。2.选择一个一条红色边,后面的每个店都有两条入边,所以是 \(2^{k-1}\)。
luogu - P10107 [GDKOI2023 提高组] 树
做法1:双 log 的,用到长链剖分。
- 显然要先拆位。
- 考虑第 \(d\) 位,显然每往下 \(2^(d+1)\) 层会有一个 \(1\)。
- 我们需要对每个点得到两个数组 \(f\),其中 \(f_i = v_i + f_{i + 2^{d+1}}\) 和 \(g_i = v_i + g_{i+1}\)(其中 \(i\) 是深度,这个式子不太严谨,不过能理解我意思吧?)
- 可长链剖分。
做法2:单 log 的,优美差分。
- 下次遇到这种求子树内距离不超过 \(k\) 的点,这种题都可以使用这种差分思想。
- 考虑这样的图:
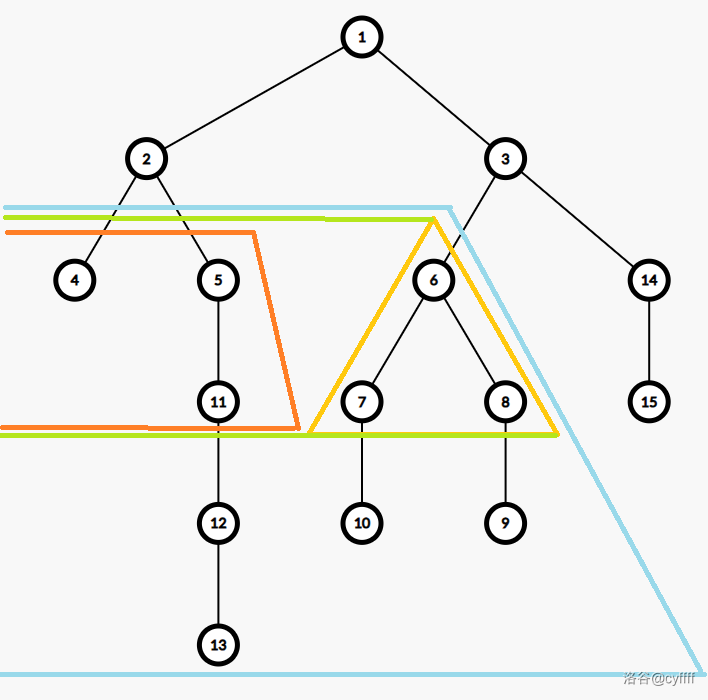
- 需要求黄色部分的答案。可以是绿色部分减去橙色部分。至于如何求这两部分,考虑如何求绿色部分,可以使蓝色部分,减去下面那空白的部分。
- 回到这一题。
- 考虑如何计算绿色部分答案。可以先预处理出所有 \((x,2^i)\) 的答案。从高位到低位向下,考虑变化。
HDU - 5458 Stability
显然先转为加边的形式。
注意到保证图任意时刻联通,那么最后也是联通的,随意建立一颗生成树。
两点之间的割边,一定出现在树上两点之间。
对于一条树边,判断树上左右两个集合,在原图上是否有另外一条边连接。设没有则边权为 \(1\),否则边权为 \(0\),那么每次询问就是求树上两点距离。
对于每次加边,也就是对一条路径上的边权 \(ckmax\)。
CF1260F - Colored Tree
参考题解:https://www.luogu.com.cn/article/6di3bksq
题解讲的很易懂了,去看题解即可。
其实自己思考的时候不用像题解一样式子从头推到尾,大部分可以感性理解。
树上最值路径
题面
树点编号1~n。统计有多少路径 u-->v
满足路径中点最大编号为u,最小编号为v。
构建一颗树:
- 从小到大枚举点,加入该点,把周围的一些集合合并。把并查集树建出来。
改为从大到小建立第二棵树。
问题变为,统计多少 \((v,u)\) 满足 \(v \le u\),且满足 \(u\) 在第一课树为 \(v\) 的祖先、\(v\) 在第二棵树为 \(u\) 的祖先。
这个问题是简单的。
TopCoder - 15434 EllysTournament
也是模拟赛的题 http://oj.daimayuan.top/contest/317/problem/2994
考虑得到一个二叉树,有多少种可能得比赛顺序会得到这样一颗树?设每个节点左右子树最底层节点个数为 \(x,y\),那么答案是所有节点的 \(\dbinom{x+y-2}{x-1}\) 乘积。
设 \(dp(x,l,r)\) 表示区间 \([l,r]\) 得到 \(x\) 为根的二叉树的概率(还要乘上上面说的那个答案)。第 \(i\) 个人的答案就是 \(\frac{dp(i,1,n)}{(n-1)!}\)。
转移容易的,但是发现需要 \(O(n^5)\)。
点击查看 $O(n^5)$ 代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const LL mod = 998244353;
const int MAXN = 503;
LL qpow(LL A, LL B){
LL ret = 1;
while(B > 0){
if(B & 1) ret = ret * A % mod;
A = A * A % mod, B >>= 1;
}
return ret;
}
inline void ADD(LL &x, LL y){ x = (x + y) % mod; }
int n;
LL fac[MAXN], ifac[MAXN];
LL a[MAXN], iw[MAXN][MAXN], pw[MAXN][MAXN], dp[MAXN][MAXN][MAXN];
LL C(int A, int B){
return fac[B] * ifac[A] % mod * ifac[B - A] % mod;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for(int i = 1; i <= n; i++){
cin >> a[i];
}
ifac[0] = fac[0] = 1;
for(int i = 1; i <= n; i++) fac[i] = fac[i - 1] * i % mod, ifac[i] = qpow(fac[i], mod - 2);
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++) iw[i][j] = qpow(a[i] + a[j], mod - 2);
}
for(int i = 0; i <= n; i++){
for(int j = 0; i + j <= n; j++) pw[i][j] = pw[j][i] = C(i, i + j);
}
for(int i = 1; i <= n; i++) dp[i][i][i] = 1;
for(int l = 2; l <= n; l++){
for(int i = 1; i <= n - l + 1; i++){
int j = i + l - 1;
for(int x = i; x <= j; x++){
for(int y = x + 1; y <= j; y++){
for(int h = x; h < y; h++){
ADD(dp[x][i][j], a[x] * iw[x][y] % mod * dp[x][i][h] % mod * dp[y][h + 1][j] % mod * pw[h - i][j - h - 1] % mod);
ADD(dp[y][i][j], a[y] * iw[x][y] % mod * dp[x][i][h] % mod * dp[y][h + 1][j] % mod * pw[h - i][j - h - 1] % mod);
}
}
}
}
}
for(int x = 1; x <= n; x++) cout << dp[x][1][n] * ifac[n - 1] % mod << "\n";
return 0;
}
注意到可以优化这个转移式子,得到:
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const LL mod = 998244353;
const int MAXN = 503;
LL qpow(LL A, LL B){
LL ret = 1;
while(B > 0){
if(B & 1) ret = ret * A % mod;
A = A * A % mod, B >>= 1;
}
return ret;
}
inline void ADD(LL &x, LL y){ x = (x + y) % mod; }
int n;
LL fac[MAXN], ifac[MAXN], ipw[MAXN];
LL a[MAXN], iw[MAXN][MAXN], dp[MAXN][MAXN][MAXN];
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for(int i = 1; i <= n; i++){
cin >> a[i];
}
ipw[0] = 1;
for(int i = 1; i <= n; i++) ipw[i] = qpow(i, mod - 2);
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++) iw[i][j] = qpow(a[i] + a[j], mod - 2);
}
for(int i = 1; i <= n; i++) dp[i][i][i] = 1;
for(int l = 2; l <= n; l++){
for(int i = 1; i <= n - l + 1; i++){
int j = i + l - 1;
for(int x = i; x <= j; x++){
for(int y = x + 1; y <= j; y++){
for(int h = x; h < y; h++){
ADD(dp[x][i][j], iw[x][y] * dp[x][i][h] % mod * dp[y][h + 1][j] % mod);
ADD(dp[y][i][j], iw[x][y] * dp[x][i][h] % mod * dp[y][h + 1][j] % mod);
}
}
}
for(int x = i; x <= j; x++) dp[x][i][j] = dp[x][i][j] * ipw[j - i] % mod * a[x] % mod;
}
}
for(int x = 1; x <= n; x++) cout << dp[x][1][n] << "\n";
return 0;
}
需要注意到 \(dp(x,l,r) = dp(x,l,x) \times dp(x,x,r)\),为什么?
- 可以看作是多个区间,依次与 \(x\) 合并。
- 也就是 \([l,r]\) 被分为多个区间。观察转移式子,我们不在乎区间之间的合并顺序,所以直接相乘即可。
接下来就只需要存所有 \(dp(x,l,x),dp(x,x,r)\),转移可以做到 \(O(n^3)\)。
luogu - P5314 [Ynoi2011] ODT
显然每个节点都存一个 Trie 显然空间没问题(只是指空间不会平方级别),但是修改操作就会超时。
考虑每个节点的 Trie 只存轻儿子。那么每次修改操作只会改变 \(O(\log n)\) 个 Trie。
至于每次询问需要多出几次插入、删除。
然后发现会 MLE,考虑如何卡常。感觉每次询问那里插入、删除很浪费。对于询问,只需要得到原 Trie 中的第 \(y-3,y-2,y-1,y,y+1,y+2,y+3\) 小,和那 \(3\) 个值共同存入一个 vector 中,问题就是求 vector 中的第 \(4\) 大。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号