matlab实现CL与GHM多小波
实现CL(Chui-Lian)和GHM(Geronimo-Hardin-Massopust)多小波分解的MATLAB程序,包含多种预滤波方法(重复行滤波、逼近阶滤波等)。程序支持多层分解
function [coeff] = multiwavelet_decomposition(x, type, prefilter, level)
% 多小波分解函数
% 输入:
% x: 输入信号 (行向量)
% type: 多小波类型 ('CL' 或 'GHM')
% prefilter: 预滤波方法 ('repeated' 或 'approximation')
% level: 分解层数
% 输出:
% coeff: 分解系数结构体
% .cA: 最后一层低频系数 (2×M矩阵)
% .cD: 各层高频系数 (元胞数组,每层为2×M矩阵)
% 参数检查
if nargin < 4
level = 1;
end
% 预滤波处理
if strcmpi(prefilter, 'repeated')
% 重复行预滤波
s0 = [x; x] * (1/sqrt(2));
elseif strcmpi(prefilter, 'approximation')
% 逼近阶预滤波
if mod(length(x), 2) ~= 0
x = x(1:end-1); % 确保长度偶数
warning('信号长度已截断为偶数');
end
if strcmpi(type, 'GHM')
P = [1/sqrt(2), 1/sqrt(2); 1/2, -1/2]; % GHM预滤波器
else % CL使用相同预滤波器
P = [1, 0.5; 0, 1]; % 示例预滤波器 (实际应用需调整)
end
x_even = x(1:2:end);
x_odd = x(2:2:end);
x_block = [x_even; x_odd];
s0 = P * x_block;
else
error('不支持的预滤波方法');
end
% 选择多小波滤波器
[H0, H1] = get_multiwavelet_filters(type);
% 多层分解
cA = s0;
cD = cell(1, level);
for j = 1:level
[cA, cD{j}] = decompose_one_level(cA, H0, H1);
end
% 返回系数
coeff.cA = cA;
coeff.cD = cD;
end
function [cA, cD] = decompose_one_level(s0, H0, H1)
% 单层多小波分解
% 输入:
% s0: 输入信号 (2×N矩阵)
% H0, H1: 低通和高通滤波器组 (元胞数组)
% 输出:
% cA, cD: 低频和高频系数 (2×M矩阵)
L = length(H0); % 滤波器长度
[r, N] = size(s0); % r=2 (通道数), N=信号长度
M = ceil(N/2); % 输出长度
% 补零处理边界
s0_padded = [zeros(r, L-1), s0, zeros(r, L-1)];
% 初始化输出
cA = zeros(r, M);
cD = zeros(r, M);
% 卷积和下采样
for k = 1:M
start_idx = (k-1)*2 + 1;
a_temp = zeros(r, 1);
d_temp = zeros(r, 1);
for n = 1:L
idx = start_idx + n - 1;
if idx <= size(s0_padded, 2)
a_temp = a_temp + H0{n} * s0_padded(:, idx);
d_temp = d_temp + H1{n} * s0_padded(:, idx);
end
end
cA(:, k) = a_temp;
cD(:, k) = d_temp;
end
end
function [H0, H1] = get_multiwavelet_filters(type)
% 获取多小波滤波器系数
if strcmpi(type, 'GHM')
% GHM滤波器系数
H0 = cell(1,4);
H0{1} = [3/(5*sqrt(2)), 4/5; -1/20, -3/(10*sqrt(2))];
H0{2} = [3/(5*sqrt(2)), 0; 9/20, 1/sqrt(2)];
H0{3} = [0, 0; 9/20, -3/sqrt(2)];
H0{4} = [0, 0; -1/20, 0];
H1 = cell(1,4);
H1{1} = [-1/20, -3/(10*sqrt(2)); 1/20, 3/(10*sqrt(2))];
H1{2} = [9/20, -1/sqrt(2); -9/20, 1/sqrt(2)];
H1{3} = [3/(5*sqrt(2)), 0; -3/(5*sqrt(2)), 0];
H1{4} = [0, 0; -1/20, 0];
elseif strcmpi(type, 'CL')
% CL多小波滤波器系数
H0 = cell(1,3);
H0{1} = [1/2, 1/2; -1/8, -1/8];
H0{2} = [1/2, -1/2; 1/8, -1/8];
H0{3} = [0,0; 1/4,0];
H1 = cell(1,3);
H1{1} = [0,0; -1/4,0];
H1{2} = [1/2, -1/2; -1/8, 1/8];
H1{3} = [-1/2, -1/2; 1/8, 1/8];
else
error('未知的多小波类型');
end
end
示例:
% 生成测试信号
t = linspace(0, 1, 1024);
x = sin(2*pi*10*t) + 0.5*cos(2*pi*50*t) + randn(1,1024)*0.2;
% CL多小波分解 (重复行预滤波,3层分解)
coeff_cl = multiwavelet_decomposition(x, 'CL', 'repeated', 3);
% GHM多小波分解 (逼近阶预滤波,2层分解)
coeff_ghm = multiwavelet_decomposition(x, 'GHM', 'approximation', 2);
% 可视化结果
figure;
subplot(3,1,1); plot(x); title('原始信号');
subplot(3,1,2);
plot(coeff_cl.cA(1,:)); hold on;
plot(coeff_cl.cA(2,:));
title('CL多小波第3层低频系数 (两个通道)');
legend('通道1','通道2');
subplot(3,1,3);
plot(coeff_ghm.cA(1,:)); hold on;
plot(coeff_ghm.cA(2,:));
title('GHM多小波第2层低频系数 (两个通道)');
legend('通道1','通道2');
参考代码 CL与GHM多小波matlab程序 www.youwenfan.com/contentcnl/64579.html
说明:
-
多小波类型:
'CL':Chui-Lian多小波(3阶滤波器)'GHM':Geronimo-Hardin-Massopust多小波(4阶滤波器)
-
预滤波方法:
-
'repeated':重复行滤波\(s_0 = \frac{1}{\sqrt{2}} \begin{bmatrix} x \\ x \end{bmatrix}\)
-
'approximation':逼近阶滤波![]()
-
-
多层分解:
- 支持任意层数分解
- 每层分解包含:
- 低频系数 (
cA): 2×M矩阵(两个通道) - 高频系数 (
cD): 各层高频系数存储在元胞数组中
- 低频系数 (
-
边界处理:
- 采用零填充方式处理边界
- 逼近阶滤波自动截断信号为偶数长度
-
输出结构:
coeff.cA:最后一层低频系数coeff.cD{i}:第i层高频系数

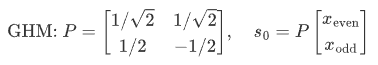

 浙公网安备 33010602011771号
浙公网安备 33010602011771号