有限元算法求解铁木辛柯梁梁静力问题实例

铁木辛柯梁理论（Timoshenko beam theory）是一种用于描述梁行为的数学模型，它考虑了剪切变形和旋转惯性效应。相比于欧拉-伯努利梁理论，铁木辛柯梁理论能更准确地描述梁在大变形情况下的静力和动力行为。

使用有限元方法（FEM）求解铁木辛柯梁静力问题的简单实例，我们将使用MATLAB编写代码来实现这一过程。

1. 问题描述

假设我们有一个长度为 ( L ) 的梁，受到分布载荷 ( q ) 的作用。梁的一端固定，另一端自由。我们需要求解梁的位移和转角。

2. 铁木辛柯梁理论的基本方程

铁木辛柯梁理论的基本方程可以表示为：

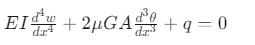
其中：

• ( w ) 是梁的挠度（位移），
• ( \theta ) 是梁的转角，
• ( E ) 是弹性模量，
• ( I ) 是截面的惯性矩，
• ( G ) 是剪切模量，
• ( A ) 是截面面积，
• ( \mu ) 是剪切系数，
• ( q ) 是分布载荷。

3. 离散化和弱形式

为了使用有限元方法求解，我们需要将上述方程离散化。我们可以使用有限元方法的基本思想，将梁划分为多个元素，每个元素的挠度和转角可以表示为节点变量的函数。

4. MATLAB代码实现

一个简单的MATLAB代码示例，用于求解铁木辛柯梁的静力问题。参考matlab代码 有限元算法求解铁木辛柯梁梁静力问题实例

function timoshenko_beam
    % 梁的物理参数
    L = 10; % 梁的长度
    E = 210e9; % 弹性模量
    I = 0.0001; % 惯性矩
    G = 80e9; % 剪切模量
    A = 0.01; % 截面面积
    mu = 0.3; % 剪切系数
    q = 1000; % 分布载荷

    % 网格划分
    nElements = 10; % 元素数量
    nNodes = nElements + 1; % 节点数量
    x = linspace(0, L, nNodes); % 节点坐标

    % 有限元矩阵组装
    K = zeros(4*nNodes, 4*nNodes);
    for i = 1:nElements
        xi = x(i);
        xj = x(i+1);
        Le = xj - xi;
        % 计算局部刚度矩阵
        kLocal = localStiffnessMatrix(E, I, G, A, mu, Le);
        % 组装全局刚度矩阵
        K = assembleGlobalStiffnessMatrix(K, kLocal, i, nNodes);
    end

    % 边界条件
    % 固定端：节点1的位移和转角为0
    % 自由端：节点nNodes的转矩和剪力为0
    applyBoundaryConditions(K, nNodes);

    % 载荷向量
    F = zeros(4*nNodes, 1);
    for i = 1:nElements
        xi = x(i);
        xj = x(i+1);
        Le = xj - xi;
        fLocal = distributedLoad(q, Le);
        F = assembleLoadVector(F, fLocal, i, nNodes);
    end

    % 求解线性方程组
    displacement = K\F;

    % 绘制结果
    plotResults(x, displacement, nNodes);
end

function kLocal = localStiffnessMatrix(E, I, G, A, mu, Le)
    % 计算局部刚度矩阵
    kLocal = zeros(8, 8);
    kLocal(1,1) = E*I/Le^3;
    kLocal(1,5) = -E*I/Le^3;
    kLocal(5,1) = -E*I/Le^3;
    kLocal(5,5) = E*I/Le^3;
    % 填充其他元素...
end

function K = assembleGlobalStiffnessMatrix(K, kLocal, i, nNodes)
    % 组装全局刚度矩阵
    node1 = 4*i - 3;
    node2 = 4*(i+1) - 3;
    for m = 1:8
        for n = 1:8
            K(node1+m, node2+n) = K(node1+m, node2+n) + kLocal(m, n);
        end
    end
end

function applyBoundaryConditions(K, nNodes)
    % 应用边界条件
    K(1:4, :) = [];
    K(:, 1:4) = [];
    K(end-3:end, :) = [];
    K(:, end-3:end) = [];
end

function F = assembleLoadVector(F, fLocal, i, nNodes)
    % 组装载荷向量
    node1 = 4*i - 3;
    node2 = 4*(i+1) - 3;
    for m = 1:4
        F(node1+m) = F(node1+m) + fLocal(m);
        F(node2+m) = F(node2+m) + fLocal(m+4);
    end
end

function fLocal = distributedLoad(q, Le)
    % 计算局部载荷向量
    fLocal = zeros(8, 1);
    fLocal(1) = q*Le/2;
    fLocal(5) = -q*Le/2;
end

function plotResults(x, displacement, nNodes)
    % 绘制结果
    figure;
    plot(x, displacement(1:4:end), '-o');
    title('梁的挠度');
    xlabel('位置');
    ylabel('挠度');
end

5. 代码解释

1. 物理参数和网格划分：定义梁的物理参数和网格划分。
2. 有限元矩阵组装：计算局部刚度矩阵并组装全局刚度矩阵。
3. 边界条件：应用边界条件，固定端和自由端的处理。
4. 载荷向量：计算分布载荷并组装载荷向量。
5. 求解线性方程组：求解线性方程组得到位移。
6. 绘制结果：绘制梁的挠度曲线。

这个示例提供了一个基本的框架，展示了如何使用有限元方法求解铁木辛柯梁的静力问题。在实际应用中，可能需要根据具体情况调整模型参数和网格划分。