树状数组学习笔记

树状数组概念

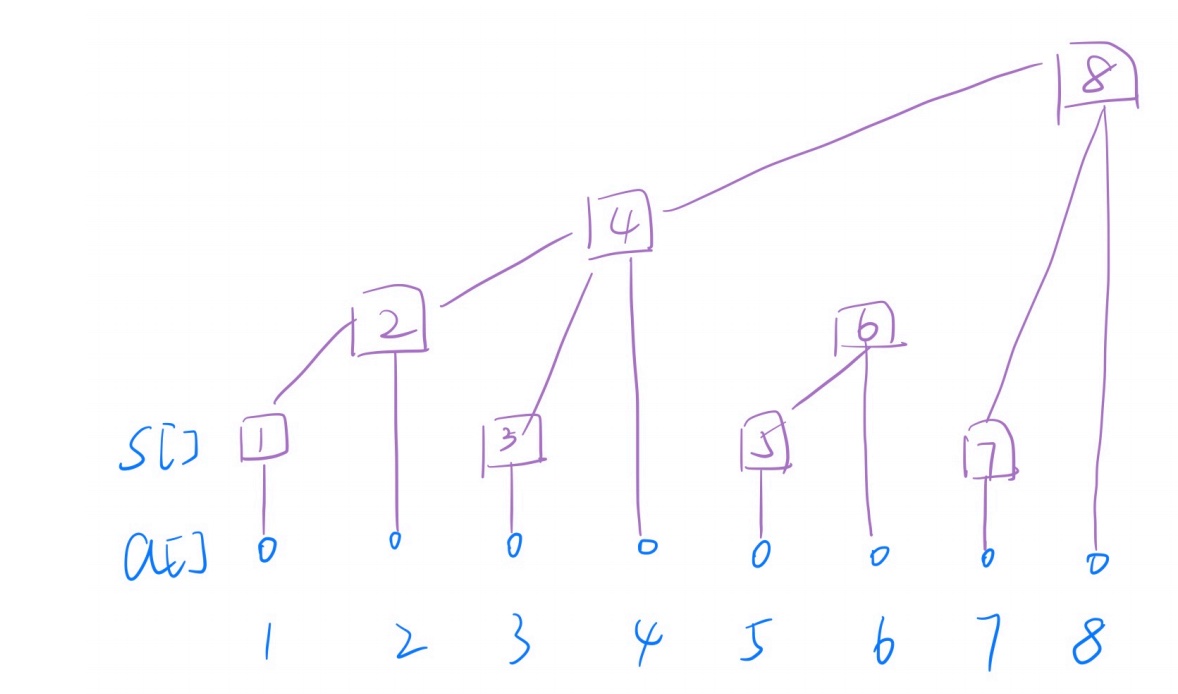
$a[i]$数组存储当前序列数据

$s[i]$ 用来存储区间和，其中下标i值代表的是一段区间，其区间长度取决于low_bit(i)

例如：

$s[4]$，4对应二进制100，因此low_bit(i) = 100，其长度为4，所以s[4]存储的为a[1]~a[4]的和。

$s[6]$，6对应二进制110，因此low_bit(i) = 10，其长度为2，所以s[6]存储的为a[5]~a[6]的和。

当需要修改a数组中某一个元素的值时，s数组对应也会发生值的变化。但树状数组支持动态维护，修改次数的时间复杂度为$log(n)$。

例：

当前n=7，如果修改$a[1]$的值，那么$s$数组对应需要发生改变的位置有：

1）第一次$x = 1$，$ s[1]$值更新

2）第二次$x = x + low_bit(x) = 2$ ,$ s[2]$更新

3）第三次$x = x + low_bit(x) = 4，$$s[4]$更新

4）第四次$x = x + low_bit(x) = 8$, 超出范围，因此s数组更新结束。

代码为：

void add(int x, int y){
		for(; x <= N; x += x & -x)		c[x] += y;
}

当需要求某一点$x$的前缀和的时候，可以利用树状数组进行求解。

其中$sum[x] = s[x] + sum[x-lowbit(x)]$，可用递推的方式求得最后结果。

例：
$sum[7]$

$= s[7] + sum[7-lowbit(7)] =s[7] + sum[6]$

$= s[7] + s[6] + sum[6-lowbit(6)] = s[7] + s[6] + sum[4]$

$= s[7] + s[6] + s[4]$

因此，求$sum[7]$只需要对三个数求和。

如果需要求解某一段区间的和，如求$l-r$之间的和，那么可用$sum[r] - sum[l-1]$。

根据数学推导可得，求解区间和时，利用树状数组可以将复杂度从$O(n)$缩小到$O(logn)$。

代码为

int ask(int x){
		int ans = 0;
		for(; x; x -= x & -x)		ans += c[x];
		return ans;
}

对于一个序列$a$，若$i<j$ 且$a[i]>a[j]$，则称$a[i]$与$a[j]$构成逆序对。

树状数组通常用来存储前缀和，给定任意一个集合$a$，当数组$t[val]$内存储的内容为$val$在集合$a$中出现的次数时，$t$数组的区间和$t[r] - t[l-1]$即表示在集合$a$中值区间为$[l,r]$的元素的个数和。因此可以利用树状数组来维护$t$的前缀和。