哈希表与字符串哈希

哈希表

哈希表：把相对复杂的数据\((0～10^9)\)集合映射到一个较小的数据集合中，通常映射到\((0～10^5)\)或\((0～10^6)\)，一般来说，有两种基础操作，添加和查找，实现的时间复杂度为\(O(1)\)

哈希函数所要考虑的

1）哈希函数的写法，如x mod 大质数

2）发生冲突时，应如何寻找值（开放寻址法、拉链法）

哈希表存储结构

1）开放寻址法

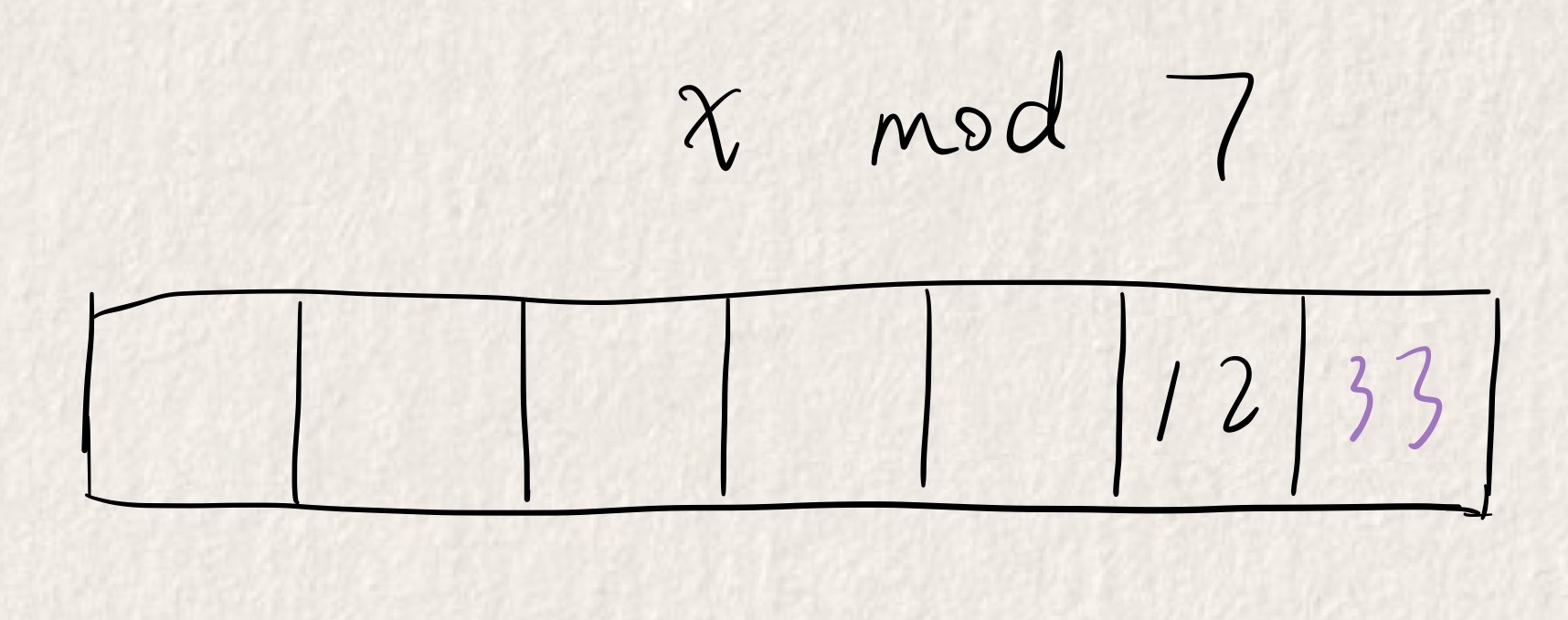
插入操作：从应放置的t位置开始判断，一旦有一个空的位置就将其插入。

查找操作：从从应放置的t位置开始搜索，如果遇到值则返回，若遇到第一个不为空的位置不等于查找的值，则查找不到该值。

注意事项：如果数据范围为\(10^5\),那么开放寻址法的数组大小要开到原范围的2～3倍， 即\(3*10^5\)。

const int N = 200003, null = 0x3f3f3f3f;
int h[N];
//如果x在哈希表中已经存在，那么返回的是所在位置下标，如果不存在则返回当前应该在哈希表中存储的位置。
int find(int x)
{
    int t = (x % N + N) % N;
    while (h[t] != null && h[t] != x)
    {
        t ++ ;
        if (t == N) t = 0;
    }
    return t;
}

2）拉链法

用一个一维数组来存储所有的哈希值，如果有值发生冲突，则在原本位置连接新值。

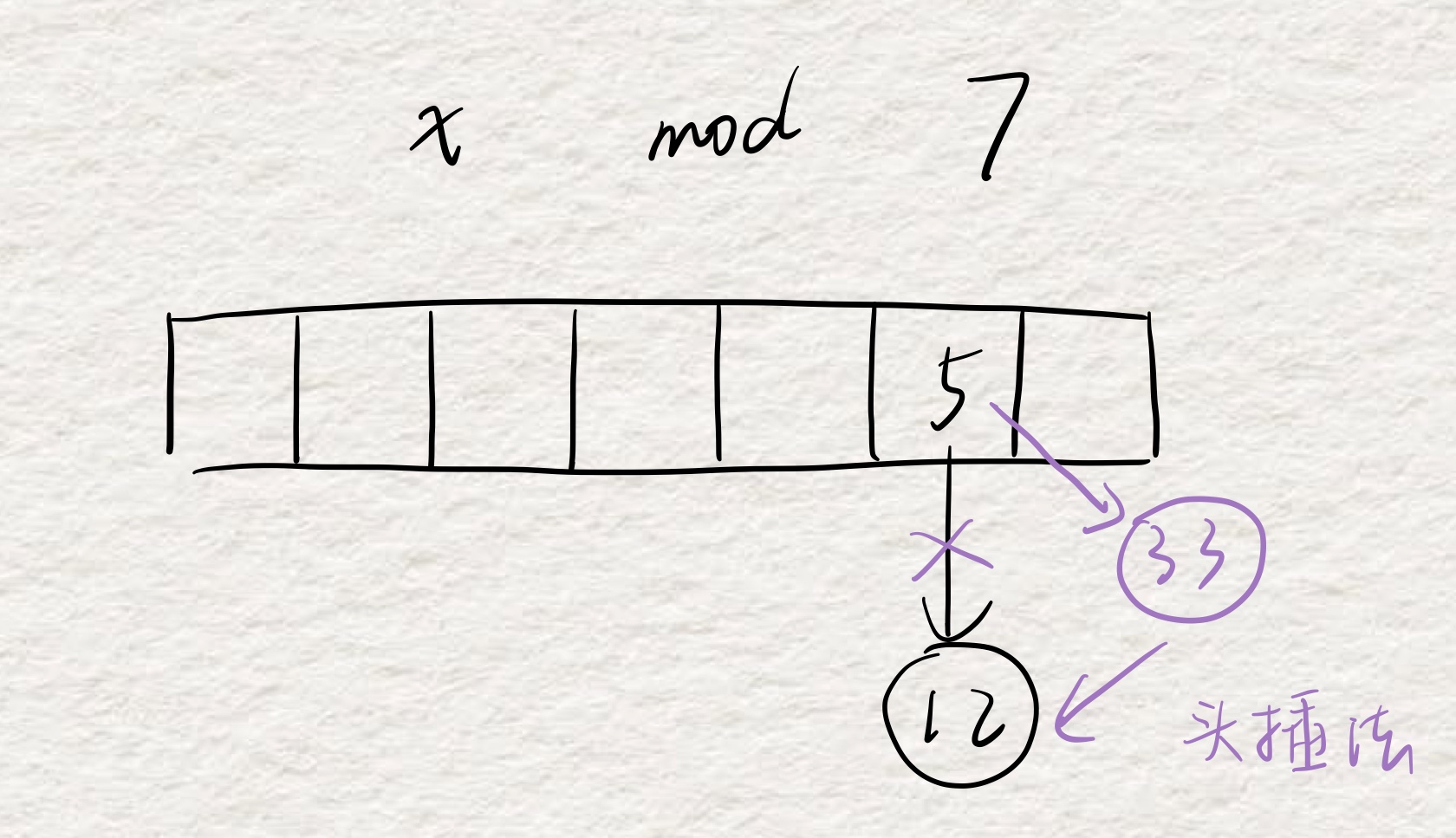
//向哈希表中添加元素
const int N = 100003;
//h数组表示
int h[N], e[N], ne[N], idx;
//链表头插法
void insert(int x){
	//重要写法，因为x可能为一个很小的负数。
	int k = (x % N + N) % N;
	e[idx] = x;
	ne[idx] = h[k];
	h[k] = idx ++;
}

//在哈希表中查找元素
bool find(int x){
	int k = (x % N + N) % N;
	for(int i = h[k]; i != -1; i = ne[i]){
		if(e[i] == x)	return true;
	}
	return false;
}

字符串哈希

定义

我们定义一个把字符串映射到整数的函数\(f\)，这个\(f\)称为是 Hash 函数。

我们希望这个函数\(f\)可以方便地帮我们判断两个字符串是否相等。

性质

具体来说，哈希函数最重要的性质可以概括为下面两条：

1. 在 Hash 函数值不一样的时候，两个字符串一定不一样；

2. 在 Hash 函数值一样的时候，两个字符串不一定一样（但有大概率一样，且我们当然希望它们总是一样的）。

   我们将 Hash 函数值一样但原字符串不一样的现象称为哈希碰撞。

构造方法

通常我们采用的是多项式 Hash 的方法，对于一个长度为\(l\)的字符串\(s\)来说，我们可以这样定义多项式 Hash 函数：

\(f(s)=\sum_{i=1}^ls[i]*p^{l-i}(mod \quad M)\)

例如，对于字符串\(xyz\)来说，其哈希函数的值为\(xp^2+yp+z\)

在选定\(p\)和\(M\)时，两者都最好选一个较大的质数，可以降低哈希的冲突率。

在这里推荐\(p\)的取值为\(131\)或 \(1331\)或 \(1313131\)

\(M\)一般取大质数，还可以将\(M\)的值设成\(2^{64}\)，并且将\(hash\)数组的值类型设置成\(ULL\)。利用\(ULL\)的取值范围正好在\([0,2^{64}-1]\)，用值的自然溢出代替取模。

字符串子串的哈希值获取

通过计算该字符串的所有前缀的哈希值，可以获得该字符串对应的所有子串的哈希值。

如对于字符串“ABCD”，要单独处理“A”、“AB”、“ABC”、“ABCD”四个前缀的哈希值。

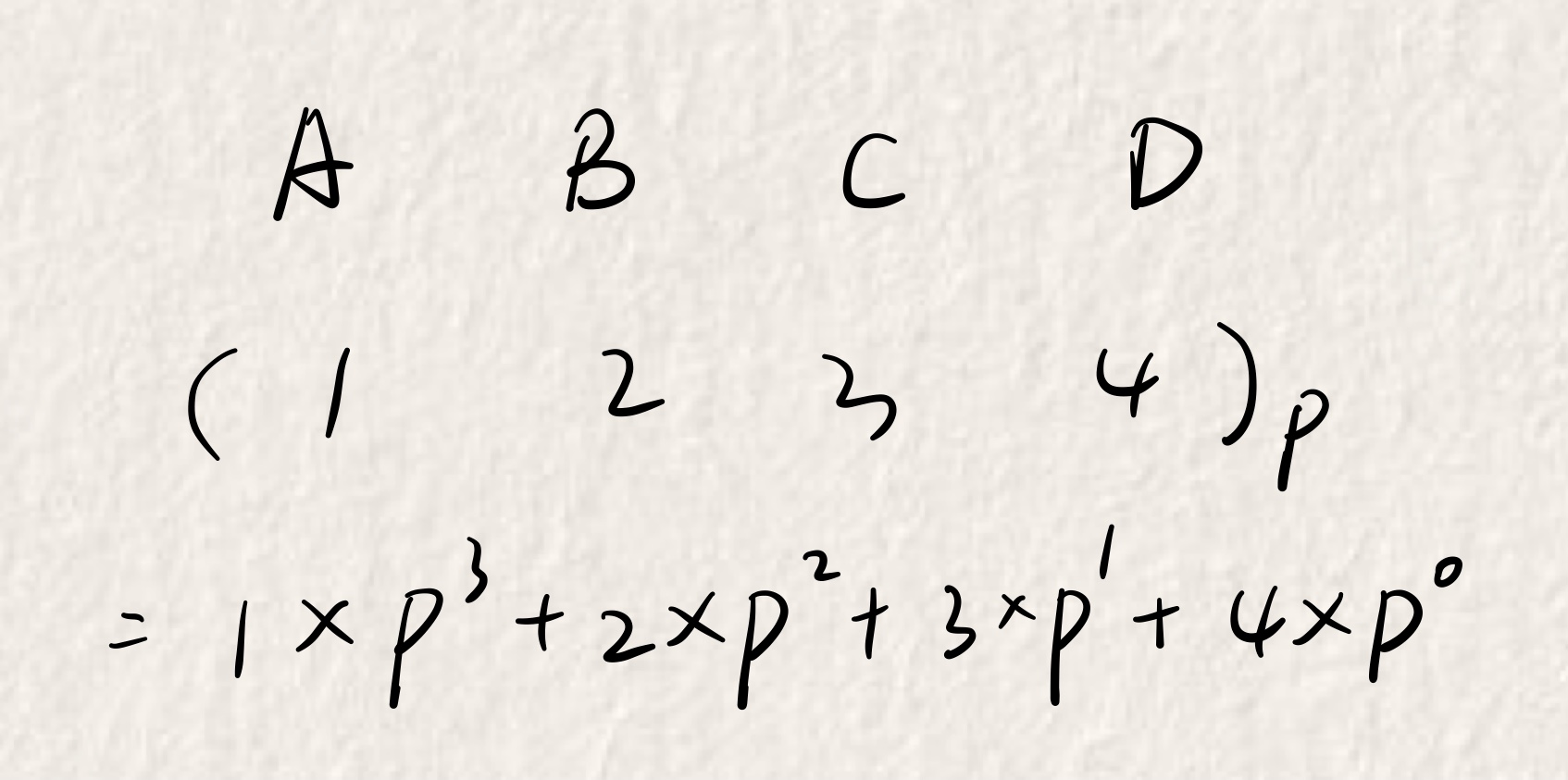
1）把该字符串看作是一个\(P\)进制的数

2）把该字符串所对应的\(P\)进制数转换为十进制数，再mod \(M\)

经过以上两步操作，可以将一个任意的字符串转换成\((0, M-1)\)区间的一个数。

注意：

1）不能将字母映射成0。

2）该情况假定不存在冲突

常用实现方式：双值哈希

用两个mod值来验证是否是同一个字符串，从而减小其哈希冲突的概率

#include<iostream>
#include<stdio.h>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;

struct mo{
    int mo1;
    int mo2;
}m[100005];

bool cmp(mo a, mo b){
    if(a.mo1 != b.mo1)      return a.mo1 < b.mo1;
    else return a.mo2 < b.mo2;
}

int main()
{
    int n, ans = 1;
    string s;
    ll hash_val[100005];
    cin >> n;
    for(int i = 1; i <= n; i++){
        cin >> s;
        for(int j = 0; j < s.length(); j++)		hash_val[i] = (hash_val[i] * 62) + s[j];
        //判断冲突
        m[i].mo1 = hash_val[i] % ll(1e9 + 7);
        m[i].mo2 = hash_val[i] % ll(1e9 + 9);
    }
    sort(m + 1, m + n + 1, cmp);
    for(int i = 1; i < n; i++){
        if(m[i].mo1 == m[i+1].mo1 && m[i].mo2 == m[i+1].mo2)    continue;
        ans ++;
    }
    cout << ans << endl;
    return 0;
}