KMP算法
KMP字符串匹配算法
大概步骤:
以在ababcabaa中查找ababa为例
- 第一步 : 对比较短的字符串计算前缀表
如 ababc的前缀有
a
ab
aba
abab
ababa
后缀有
c
bc
abc
babc
ababc
①计算出每个前缀中前后缀相等的长度(长度小于前缀本身的长度)
如abab这个前缀,长度为4,所以要找到长度小于4的前缀和后缀,使其
相等
如
abab长度为3的前缀为aba
abab长度为3的后缀为bab
不相等,长度减1
abab长度为2的前缀为ab
abab长度为2的后缀为ab
相等,则得到该前缀的前缀表值为2
由上得到
a --0
ab --0
aba --1
abab --2
ababa --3
因为前缀为ababa时说明已经找到了,所以没必要要最后一行,而是在第一行加-1
所以得到前缀表为
| a | b | a | b | c |
|---|---|---|---|---|
| -1 | 0 | 0 | 1 | 2 |
- 第二步进行遍历匹配
i用来遍历较长的字符串s,j用来遍历较短的字符串d- 当s[i] == d[j] 时,i++,j++。即两个都往后移一格
- 但s[i] != d[j]时,把 j 所对应的前缀表的值给j,即把d字符串的j位置与当前s字符串的i位置对齐
- 但j被赋值为-1时,i++;j++; 即 i 和 j 都向下移一格
- 被赋值为非-1时正常处理
下面进行演示
s为较长字符串,d为较短字符串,q为前缀表
初始状态

i=0,j=0时相同
执行i++;j++;
i = 1; j = 1;
i = 2; j = 2;时也都相同执行i++;j++;

直到i=3时,s[i] = A,d[j] = B;s[i] != d[j]
执行j = q[j] 变为

s[i] != d[j]
执行j = q[j] 变为

此时s[i] == d[j]

s[i] != d[j]
执行j = q[j] 变为

s[i] != d[j]
执行j = q[j] 变为

s[i] != d[j]
执行j = q[j] ;
但是这里q[0] = -1;而数组没有-1这个下标,所以就直接跳过这一对

i = 5,6,7,8,9。这些情况都是s[i] == d[j]
完成匹配

算法代码如下
//生成原始前缀表的函数
void prefix_table(string d,int prefix[],int n)
{
prefix[0] = 0;
int len = 0;
int i = 1;
while (i < n)
{
if (d[i] == d[len]) {
len++;
prefix[i] = len;
i++;
}
else
{
if (len > 0) {
len = prefix[len - 1];
}
else
{
prefix[i] = 0;
i++;
}
}
}
}
- 代码解释

①相同的情况
②不同的情况

是不是直接等于0呢?
我们来看一下最后一个
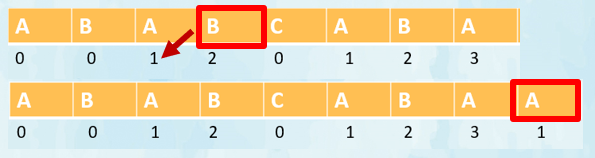
这里不相同但是也不等于零,而是等于了前一个元素公共前后缀的值
这里既然等于前一个的,那么等于0的前一个就是-1,所以,在前一个为-1时就可以直接赋值为0;
void move_prefix_table(int prefix[], int n) {//移位函数
int i;
for (i = n-1; i > 0; i--)
{
prefix[i] = prefix[i - 1];
}
prefix[0] = -1;
}
//把前缀表整体后移一位,第一位赋值为-1
void kmp_search(string s, string d)
{
int n = d.size();//需要查找的字符串(短)
int m = s.size();
int* prefix = new int[n];
prefix_table(d, prefix, n);
move_prefix_table(prefix, n);
int i, j;
i = 0; j = 0;
bool k = false;
while (i < m)
{
if (j == n - 1 && d[j] == s[i])//找到了完整的串
{
k = true;
cout << "FIND IN " << i - j << endl;
j = prefix[j];//继续寻找看看还有没有
if (j == -1)
{
i++;
j++;
}
}
if (s[i] == d[j])
{
i++;
j++;
}
else
{
j = prefix[j];
if (j == -1)
{
i++;
j++;
}
}
}
if(!k)//找不到
cout << "找不到" << endl;
delete []prefix;
}
样例测试
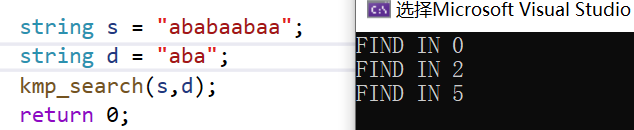
本文来自博客园,作者:墨镜一戴谁也不爱,转载请注明原文链接:https://www.cnblogs.com/hnuzmh/p/16196570.html




 浙公网安备 33010602011771号
浙公网安备 33010602011771号