SVM——针对线性可分（上）

看了好多大佬的文章，怕看完就忘，简单整理一下。

支持向量机原理(一) 线性支持向量机 - 刘建平Pinard - 博客园 (cnblogs.com)

机器学习之支持向量机（一）：支持向量机的公式推导 - 追寻的鹿 - 博客园 (cnblogs.com)

用人话讲明白支持向量机SVM（上） - 知乎 (zhihu.com)

码一下我看的几篇文章，以防看不懂可以翻一翻大佬写的。

一、认识支持向量机

1. 支持向量机是处理数据分类问题，一般是用于解决二分类问题，线性分类和非线性分类都支持；
2. 目的是学会一个二分类的函数模型，属于监督式学习的方法，被广泛应用于统计分类和回归分析；
3. 通过建立一个超平面对样本数据进行分类，超平面涉及到凸优化、拉格朗日乘数法、对偶问题的应用；
4. 本文以线性可分为例，来找最优的超平面。

二、线性可分和线性不可分

（1）线性可分

　　线性可分是指能使用线性组合组成的超平面将两类集合分开。

　　比如一维空间的点，二维空间的直线，三维空间的平面，高维空间叫超平面。

（2）线性不可分

　　线性不可分则没有能将两类集合分开的超平面。

　　主要通过松弛变量、核函数来实现。

　　例如：二维线性可分、二维线性不可分、三维线性可分、三维线性不可分

 

 

 

 

 

 

三、符号定义

（1）样本数据

　　n个样本；

　　每个样本有p个输入   ，1个输出；（p为维数）

　　则第i个样本的输入： ；

　　输出y：一般用1和-1作为两类样本的标签；

（2）样本训练集

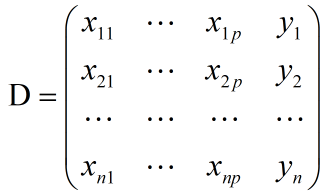
（3）训练目的

　　以训练样本作为研究对象；

　　找到一个超平面；其中；

　　将两类样本有效分开；

　　该公式的来源我们继续往下看。。。。。

四、线性分类器的含义

 　　为了方便理解，我们以二维为例，先了解一下线性分类器：

 

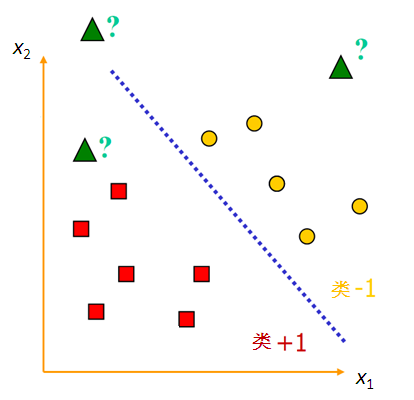
　　红色方形的标签为1，黄色圆点的标签为-1（自己定义的，后续会说定义为1的原因。。。）

　　蓝色直线为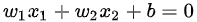

 　　  的区域是y=1类别的点（为什么>0的区域是1而不是-1呢，后续会解释。。。）

  　　 的区域是y=-1类别的点

 　　推论（由二维推到高维度）

　　 

　　 转换成矩阵的形式为： （其中W是一个列向量，即(w1,w2,……,wp)^T）

五、如何找线性分类器

　　最好分类器的定义：最大边界超平面，即距两个类别的边界观测点最远的超平面。

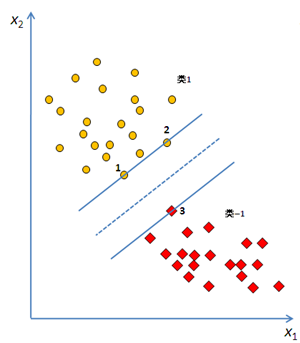
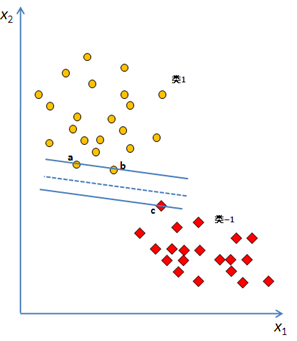
 　　图中1、2、3为支持向量（即边界观测点），中间的虚线为我们想要找到的超平面；

　　左右两图哪一个超平面更好呢？为此我们引入一个评判指标，叫做”分类间隔“；

　　通俗来说，找一个超平面，使得离该超平面最近的点可以最远（这样子可以使容错功能越强）；

六、求解最优超平面

（1）分类间隔

　　　a.函数间隔

　　这里来解释为什么为什么将 的区域的标签定义为1，

　　而将的区域的标签定义为-1（第i个样本标签用y_i表示）

　　上述定义的内容用公式表示即为 ：

　　   y=1

　　   y=-1

　　我们可以把上述两个式子合并为：（该值永远大于0，正好符合了距离的概念）

　　我们把样本点（Xi,y_i）的函数间隔定义为：（假设y=1时，原来的超平面是f(x)=0，若y=1,f(x)=1，相当于向右平移了一个单位，所以f(x)值越大的点到分类超平面的距离当然越远）

　　我们选取超平面与训练集中样本的函数间隔最小值，记为

 

　　我们只需要最大化即可（但存在一个问题，如果w和b变为2w和2b，此时超平面没有改变，但是函数间隔却变大了）

 

 　（注意到函数间隔实际上并不能表示点到超平面的距离，所以定义点到超平面的距离时，我们采用下面的几何间隔）

　　　b.几何间隔

　　由点到直线距离公式可知，样本点X_i到超平面的距离为：

 

 

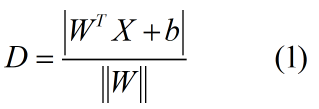
 　　其中，||W||表示向量的2-范数，我们把这个D叫做几何间隔，也就是最终我们要求支持向量到超平面的几何间隔最大值

（2）凸二次规划

 

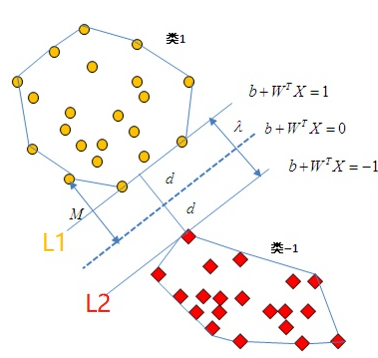
　　我们把中间的超平面用来表示

　　把L1定义为：，把L2定义为

 　（为什么方程是1和-1，其实也可以是任意非零常数C和-C，规定1和-1是为了方便）

　　于是可得：

 

 

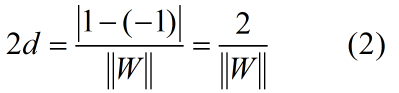
 　　我们需要最大化d:

 

 

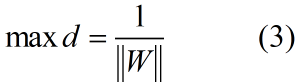
 　　(3)式可以等价为：

 

 

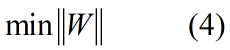
 　　我们通常会把（4）式转换为：

　　

 

 

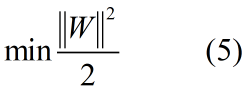
 　　除了距离以外，我们还有限制条件，超平面正确分类意味着点i到超平面的距离恒大于等于d：

　　

 

 

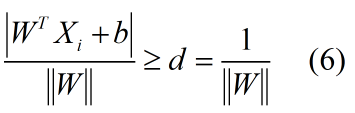
 　　我们可以把式（6）化简为：

　　

 

 

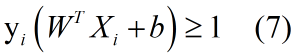
　　目标函数：

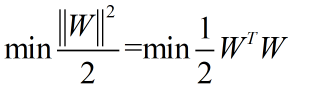
　　约束条件：

 

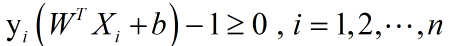
　　这种规划问题叫做凸二次规划。

（3）拉格朗日乘数法

　　那么如何求解这种不等式条件约束下的求多元函数极值的问题呢？

　　我们采用拉格朗日乘数法，通过引入新的未知标量（拉格朗日乘数  ），直接求多元函数条件极值

　　我们将目标函数和约束条件整合为：

 

 

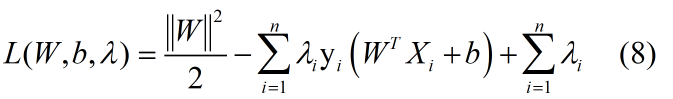
 　　其中

 

　　 引入了拉格朗日乘子，我们的优化目标变为：

 

 

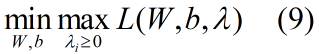
 　　如何化简式(9)呢，我们引入一个对偶的概念

（4）对偶问题

　　 我们把(9)式通过对偶转化为(10)式：

 

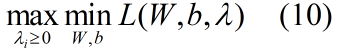
　　 通过上式我们可以先求优化函数对于W和b的极小值，接着再求拉格朗日乘子λ的极大值

　　 首先求定义：

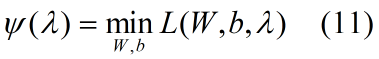
　　 接下来求偏导得到：

 

 

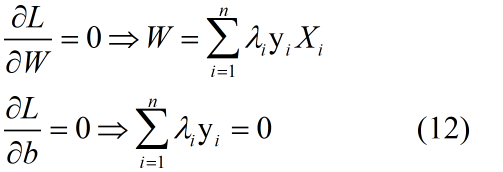
　　 我们将(12)式代入到(11)式可得：

 

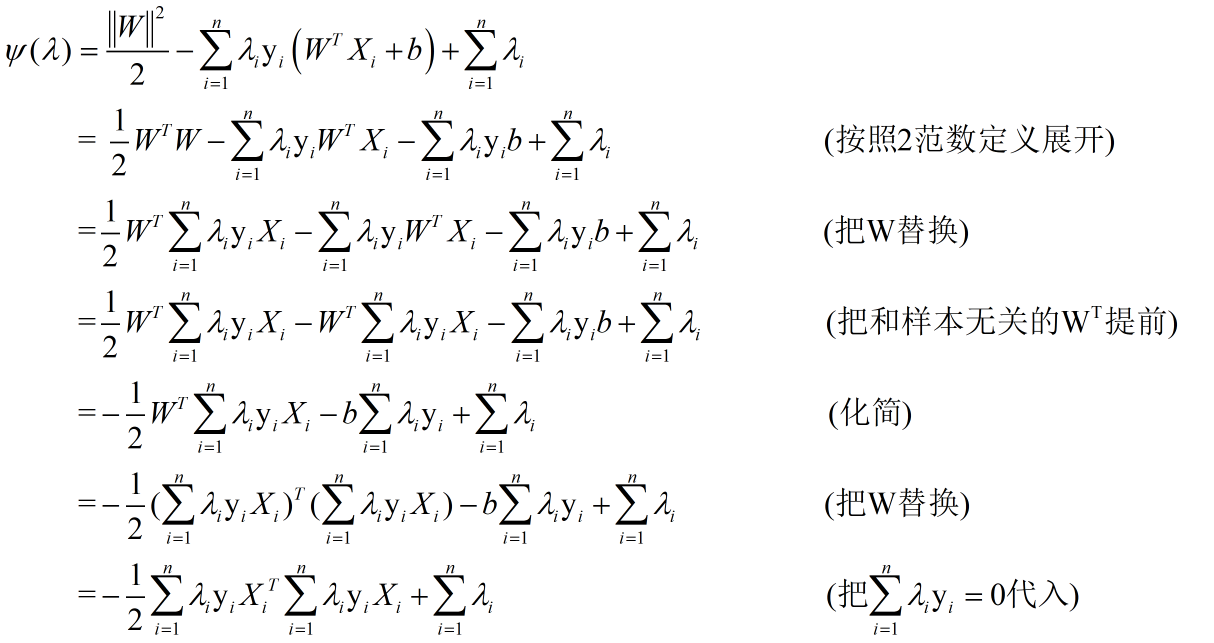
 　　 于是我们将整体目标函数化简为：

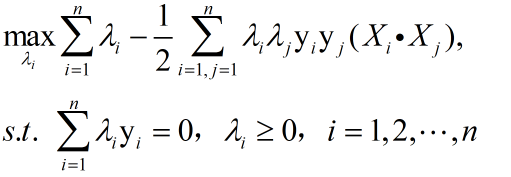
　　 将上述问题等价为极小化问题如下：

 

 

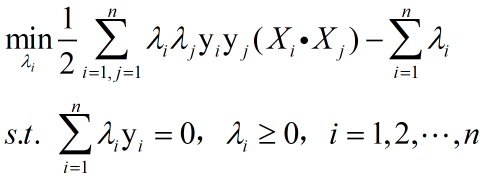
　　只要我们可以求出极小化时对应的λ向量就可以求出W和b了，那么怎么极小化上式得到对应的λ呢，一般要用到SMO算法。