图神经网络的表达能力与置换同变性

目录

• 图神经网络的表达能力与置换同变性
  • 表达能力与泛化性
  • 置换同变图神经网络

图神经网络的表达能力与置换同变性

图神经网络（Graph Neural Networks, GNN）接替网络嵌入（Network Embedding）成为图机器学习的主流，并渗透到计算机视觉和自然语言处理领域，取得了巨大的成功。现有的 GNN 大多可以纳入消息传递（Message Passing Neural Networks, MPNN）的框架下，在图数据结构上进行信息传播和聚合。换言之，GNN 是一套在图上定义计算的学习范式，它能够利用图结构，但是并不承诺保持图结构，而保持图结构恰恰是网络嵌入的宗旨。实际上，如果缺少有判别性的特征，GNN 将完败于网络嵌入（AM-GCN, KDD2020）。也就是说，现有的 GNN 并不是万能的，远非图机器学习的最终形态。那 GNN 的能力上限到底是什么呢？这个灵魂之问问的就是 GNN 的表达能力。

MIT 的博士生 Keyulu Xu 在 ICLR 2019上发表的论文 How Powerful are Graph Neural Networks? [1] 首次回答了这个问题，也开启了 GNN 表达能力这个研究方向，并启发研究者跳出消息传递机制的窠臼，开发具有更强的表达能力的图神经网络。很不幸，研究 GNN 表达能力的论文涉及的数学大多艰深难懂，笔者无力从数学原理上给出深入浅出的讲解。所幸的是，它们在研究思路上有相通之处，可以启发我们怎样思考 GNN 的能力和局限，并高屋建瓴地设计新的 GNN。笔者通过梳理近年的研究脉络，尝试总结 GNN 表达能力的研究思路，并介绍通往更强的 GNN 的重要线索置换同变性（Permutation Equivariance，亦译为置换等变性）及该方面的重要尝试。

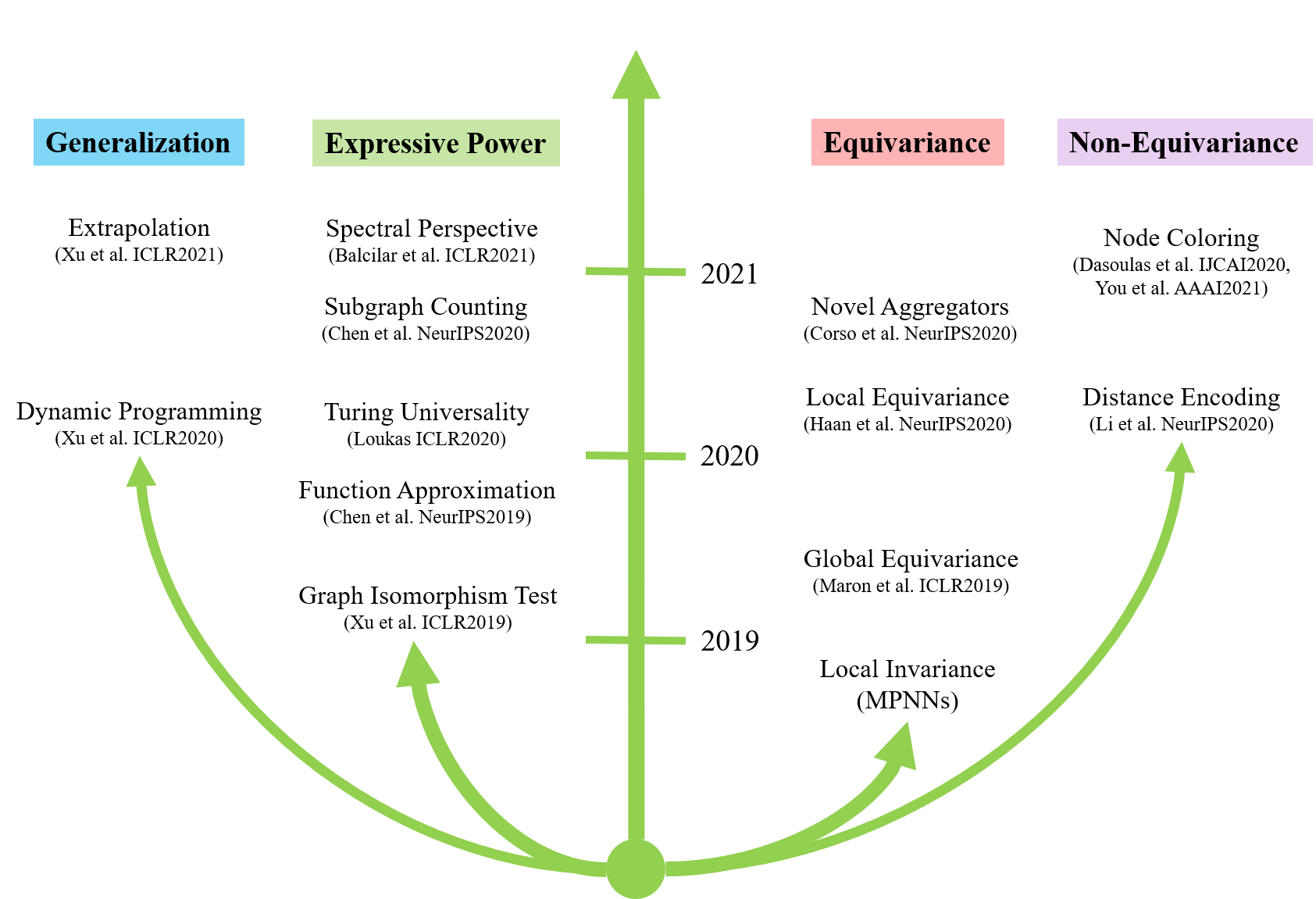
表达能力与泛化性

GNN 的表达能力（Expressive Power）研究 GNN 可以解决哪些问题，决定了 GNN 在训练集上能否过拟合，在此基础上衍生出了关于泛化性（Generalization）的研究，关心 GNN 在测试集上能否延续在训练集上的表现，下面将分别介绍。

首先我们要问，如何定义 GNN 的表达能力？一个经典的思路是函数逼近，即关心神经网络能够表达的函数的范围有多大，该方面最著名的结果是前馈神经网络的万能逼近定理（Universal Approximation Theorem）。但是 GNN 较简单的前馈神经网络增加了关于图的归纳偏置，因此该结果不能简单拓展到 GNN 上。尽管如此，我们还是可以借鉴其对表达能力的描述，即神经网络的表达能力可以描述为一个集合，这个集合代表了神经网络所有能做的事情。这一观点在计算复杂性理论里面也得到印证。该理论根据复杂度将问题分类，一类问题即复杂度一致的问题构成的集合，由此可以定义密码学中加密方案的安全性，即破解一个加密方案的难度相当于求解一个NP完全问题。据笔者观察，GNN 表达能力方面的研究正是借鉴计算复杂性的思想。比如 Xu 等人 [7] 将 GNN 的表达能力归结为图同构检验（Graph Isomporphism Test），Loukas [5] 从图灵机可计算性（Turing Universality）的角度探讨 GNN 的局限性，Chen 等人 [3] 构造子图计数（Subgraph Counting）问题来区分不同的 GNN 的能力，Chen 等人 [6] 也还回归经典，证明了 GNN 可以逼近图上任意具有置换不变性的函数。下面以图同构检验为例介绍 GNN 的表达能力。

用图同构检验来刻画 GNN 的表达能力已经有很多优秀的博客详细介绍，这里笔者不过多触及细节，注重思路的介绍。首先，这类理论分析有一个很重要的假设，即

假设：图为同质图（Homogeneous Graph），且不带节点、边、图等级别的额外的属性。

这是为了简化分析，也有其合理性。使用 GNN 是希望引入图结构来补充节点属性，如果节点属性本身已经有充分的判别性，那就没 GNN 什么事儿了。另一个角度而言，如果每个节点都有唯一标记，那每个图都有唯一的表示，图同构问题也就迎刃而解了。这一假设也符合实际，比如说不同的节点可以有相同的类标，节点属性是有混淆性的。不过也应该注意到，这个假设割裂了图结构和图属性，而两者可能是有互动的，因此笔者认为基于该假设的分析不一定能够完全解释 GNN 的表达能力。

假设做好了，可是我们为什么要关心图同构检验呢？有两方面的原因

1. 希望 GNN 有足够的特征抽取能力，能够在隐空间区分不同的图，即判断两个图是否重构
2. 形式上，GNN 的核心操作——聚合算子与图同构领域的有效算法 Weisfeiler-Lehman（WL test）的聚合操作惊人地相似

正如 GCN 可以用 \(H^l=\sigma(AH^{l-1}W)\) 概括，MPNN 也可以用以下公式概括（Pytorch Geometric）

\[\mathbf{h}^{l}_i = \gamma \left( \mathbf{h}^{l-1}_i, \underset{j \in \mathcal{N}(i)}{\square}\phi\left(\mathbf{h}^{l-1}_i, \mathbf{h}^{l-1}_j\right) \right),\tag{1} \]

其中，\(\phi,\gamma,\square\) 分别表示消息函数、更新函数和聚合函数，聚合函数满足置换不变性（Permutation Invariance），即把邻居节点的整体视为一个集合，相当于一个无序的序列，\(\square\) 的输出结果与输入节点顺序无关。常用的聚合算子有 sum，mean 和 max。

类似地，WL test 也可以用以下公式概括

\[\mathbf{c}^l_i = \text{Hash} \left( \mathbf{c}^{l-1}_i, \{\mathbf{c}^{l-1}_j\,|\,j \in \mathcal{N}(i)\} \right),\tag{2} \]

不过这里的聚合仅仅是把邻居节点的染色标记 \(\mathbf{c}^{l-1}_i\) 攒到一起而已。

可以看到，忽略消息函数 \(\phi\) 之后，通过把 MPNN 的更新函数 \(\gamma\) 和聚合函数 \(\square\) 跟 WL test 的 \(\text{Hash}\) 函数和标记收集函数分别对应起来，则建立了 MPNN 跟 WL test 的对应关系，因此 MPNN 的表达能力可以用 WL test 来刻画。自然，WL test 的局限性就对应为 MPNN 的局限性。从公式（2）可知，当每个节点的度数相等（k-regular graph，正规图）时，迭代过程中节点特征保持一致，无法通过计数的方法判断图同构。即 MPNN 无法区分正规图。可以参看 Sato 在其综述 [16] 所举的例子

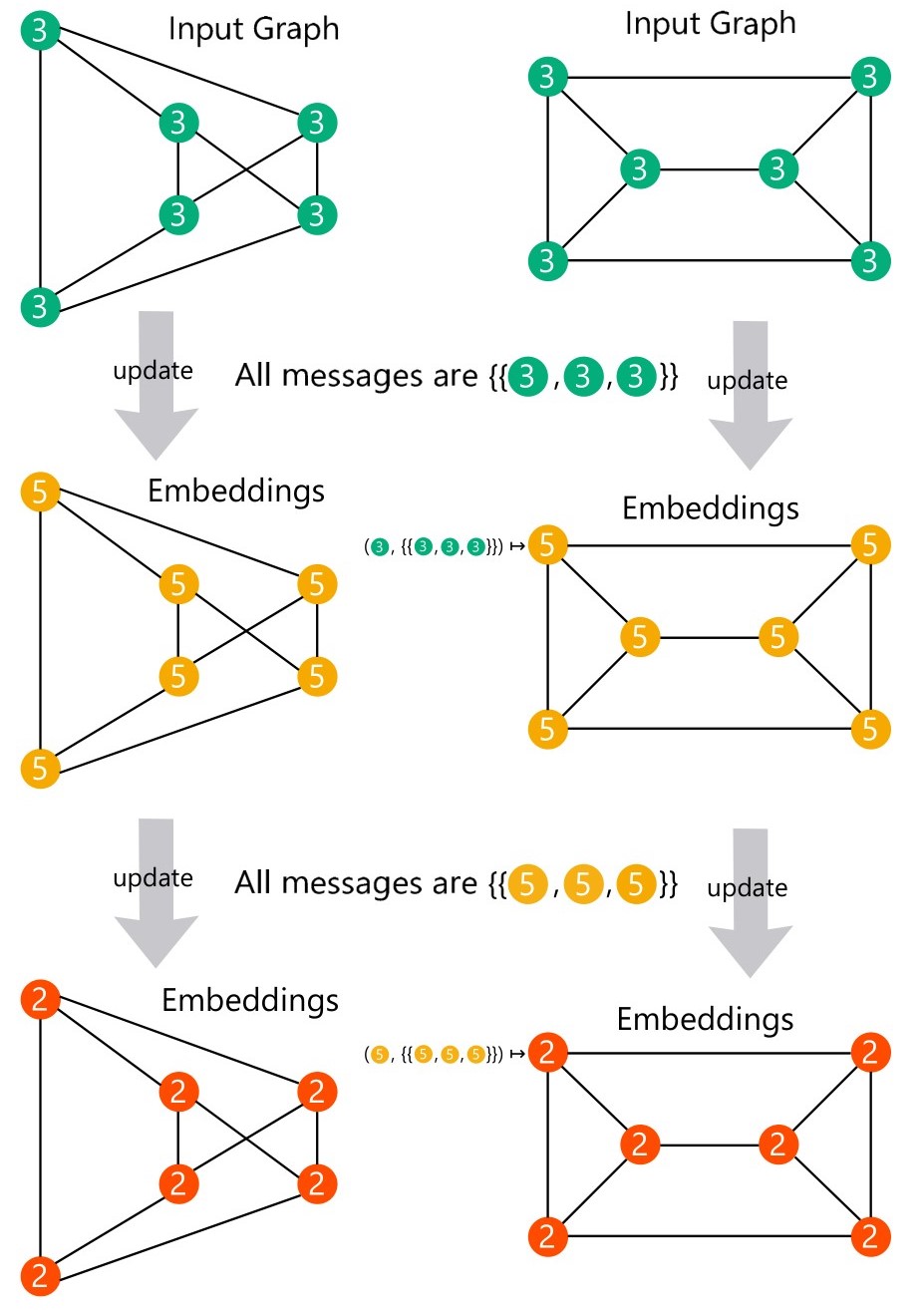
到这里似乎对 GNN 的表达能力有了比较自洽的回答，但是这个答案并不完全令人满意。其一，图同构问题已经被证明有拟多项式算法 [18]，即图同构问题并非NP完全问题，这给 GNN 表达能力上限做出了比较悲观的限制。其二，图同构问题衡量的是图级别的表达能力，但是我们常常关也心节点表示，该理论能否解释节点表达能力仍存疑。不过瑕不掩瑜，这个结果给出了 GNN 表达能力研究很好的示范，即

寻找 GNN 与经典图算法之间的对应关系，用经典算法的能力衡量 GNN 的能力，根据经典算法的局限启发新的 GNN 的设计。

泛化性方面主要是 Xu 等人 [1, 4] 在发力。跟表达能力方面的研究类似，Xu 等人找到了动态规划中的 Bellman-Ford 算法（最短路径算法）作为 MPNN 的对应

\[d^l_i = \underset{j\in\mathcal{N}_i}{\text{min}} \{d^{l-1}_j + w_{ji} \}.\tag{3} \]

至此，GNN 的泛化性可以归结为动态规划的泛化性。实际上，图同构检验和动态规划都是与数据无关的，都具有很好的泛化性，采用动态规划来描述泛化性可能是因为很多问题可以更直接地用动态规划求解吧。同样应该注意到，动态规划解决的是图级别的任务，可能无法完全回答节点级别的泛化问题。

置换同变图神经网络

从表达能力的分析可知，现有 GNN 的能力瓶颈恰恰在于其聚合算子的置换不变性。这是 GNN 设计的必要元素吗？不是，但它是设计一个置换同变的 GNN 的充分条件。什么叫置换同变性，与置换不变性有什么区别，为什么需要置换同变性？记 \(\pi\) 为节点的一个置换（乱序排列），\(f,g\) 为定义在节点特征 \(\mathbf{H}\) 的映射，称为 \(f\) 为置换不变的，如果

\[f\circ\pi (\mathbf{H}) = f(\mathbf{H}),\tag{4} \]

称 \(g\) 是置换同变的，如果

\[g\circ\pi (\mathbf{H}) = \pi\circ g(\mathbf{H}),\tag{5} \]

用人话来说，

置换不变性使得输出与输入顺序无关，而置换同变性使得输出顺序与输入顺序对应。

举个简单的例子，

\[\begin{aligned} f([\mathbf{h}_2,\mathbf{h}_1])&=f([\mathbf{h}_1,\mathbf{h}_2]),\\ g([\mathbf{h}_2,\mathbf{h}_1])&=[g(\mathbf{h})_2,g(\mathbf{h})_1].\\ \end{aligned}\tag{6} \]

显然置换同变函数后面接一个置换不变的函数，得到的函数还是置换不变的。

什么时候需要这两类函数？因为图天然具有无序性，当我们关心节点特征时，我们希望改变节点标号时，节点特征不变，或者说节点特征的排序要根据节点编号做出重排，这时候就需要置换同变性；当我们关心图特征时，希望改变节点标号不影响图特征，就需要置换不变性。显然公式（3）整体是满足置换同变性的。

Haan 等人 [10] 将 GNN 的置换同变性称为全局同变性（Global Equivariance），将聚合算子的置换不变性称为局部不变性（Local Invariance），显然

局部不变性诱导全局同变性。

通过前面的分析可知，以置换同变性为焦点，改 GNN 的路径有4条

1. 延续置换不变性，设计更强的聚合算子
2. 打破置换不变性约束，设计更强的聚合算子
3. 舍弃聚合算子，直接定义置换同变的 GNN
4. 舍弃置换同变性，设计更强的 GNN

当然，以上4条途径并非笔者原创，皆是来自文献总结。罗列如下

方法	文章	评注
更强的置换不变聚合算子	1. Principal Neighbourhood Aggregation for Graph Nets (NeurIPS2020) 2. DeeperGCN: All You Need to Train Deeper GCNs (CoRR2020)	1. 矩归一化聚合算子扩展mean 2. mean的连续延拓
更强的置换同变聚合算子	Natural Graph Networks (NeurIPS2020)	引入具有局部同变性的聚合算子保持子图结构，但实际效果并非SOTA
全局同变 GNN	1. Invariant and Equivariant Graph Networks (ICLR2019) 2. Provably Powerful Graph Networks (NeurIPS2020)	1. 直接对全图定义置换同变线性映射，仅适用于特定节点数量的图，仅有理论意义 2. 前述工作的延续，给出了可实际应用的、等价于 k 阶 WL test 的 GNN
非置换同变 GNN	1. Coloring Graph Neural Networks for Node Disambiguation (IJCAI2020) 2. Distance Encoding – Design Provably More Powerful GNNs for Structural Representation Learning (NeurIPS2020) 3. Identity-aware Graph Neural Networks (AAAI2021)	1. 对节点随机染色，根据染色不同区分聚合，结果不稳定 2. 定义每个节点到目标节点的距离衡量节点的 structural role，未在经典数据集测试 3. 区分ego-net的中心节点和其他节点，采用不同的消息函数，提升显著

Vignac 等人 [17] 指出，当前比较典型的置换同变 GNN 的复杂度如下

在众多工作中，笔者私心是比较喜欢 Haan 等人 [10] 的 Natural Graph Networks 的，其洞察深刻，兼具泛用性和简洁性。该方法的核心动机为

1. 聚合算子的置换不变性对于全局的置换同变性来说，是非必要的
2. 直接定义全部同变 GNN 仅有理论价值，无实际价值

那么有没有办法设计新的不满足不变性的聚合算子，使得 GNN 整体上仍具有同变性，但是具有更强的表达能力呢？答案是肯定的，只需引入局部同变性（Local Equivariance），即

局部同变性：相同邻域结构的节点具有相同的表示。

局部同变性能够保持邻域结构，而不是像局部不变性那样简单地记录全部邻居节点。在具体实现上，Haan 等人 [10] 把消息函数和聚合函数视为一个整体，引入了在边上定义的核（kernel）\(\phi^{\mathcal{G}}_{ij}\)，核的取值随着因图及节点而异，如下

\[\mathbf{h}^{l}_i = \gamma \left( \mathbf{h}^{l-1}_i, \underset{j \in \mathcal{N}(i)}{\square}\phi^{\mathcal{G}}_{ij}\left(\mathbf{h}^{l-1}_j, \mathbf{h}^{l-1}_{\mathcal{G}_j}\right) \right),\tag{7} \]

其中 \(\mathbf{h}^{l-1}_{\mathcal{G}_j}\) 为子图表示。可以看出，该方法通过保持子图结构增强了表达能力，但是也增大了计算量，也引入了新的问题，即子图抽取。遗憾的是，作者并未开源代码，论文汇报效果亦差强人意，后人不易跟进。

最后，将本文涉及 GNN 的核心算子及对应算子归纳如下

\[\begin{aligned} &\text{GCN}&\, H^l &= \sigma(AH^{l-1}W),\\ &\text{MPNN}&\,\mathbf{h}^{l}_i &= \gamma \left( \mathbf{h}^{l-1}_i, \underset{j \in \mathcal{N}(i)}{\square}\phi\left(\mathbf{h}^{l-1}_i, \mathbf{h}^{l-1}_j\right) \right),\\ &\text{WL Test}&\,\mathbf{c}^l_i &= \text{Hash} \left( \mathbf{c}^{l-1}_i, \{\mathbf{c}^{l-1}_j\,|\,j \in \mathcal{N}(i)\} \right),\\ &\text{Dynamic Programming}&\,d^l_i &= \underset{j\in\mathcal{N}_i}{\text{min}} \{d^{l-1}_j + w_{ji} \},\\ &\text{Graph Natural Networks}&\,\mathbf{h}^{l}_i &= \gamma \left( \mathbf{h}^{l-1}_i, \underset{j \in \mathcal{N}(i)}{\square}\phi^{\mathcal{G}}_{ij}\left(\mathbf{h}^{l-1}_j, \mathbf{h}^{l-1}_{\mathcal{G}_j}\right) \right) \end{aligned} \tag{8} \]

参考文献
[1] How Neural Networks Extrapolate: From Feedforward to Graph Neural Networks. Keyulu Xu et al. ICLR 2021.
[2] Analyzing the Expressive Power of Graph Neural Networks in a Spectral Perspective. Muhammet Balcilaret al. ICLR 2021.
[3] Can Graph Neural Networks Count Substructures? Zhengdao Chen et al. NeurIPS 2020
[4] What Can Neural Networks Reason About? Keyulu X et al. ICLR2020
[5] What Graph Neural Networks Cannot Learn: Depth versus Width. Andreas Loukas. ICLR 2020.
[6] On the Equivalence between Graph Isomorphism Testing and Function Approximation with GNNs. Zhengdao Chen et al. NeurIPS 2019.
[7] How Powerful are Graph Neural Networks? Keyulu Xu et al. ICLR2019.
[8] Principal Neighbourhood Aggregation for Graph Nets. et al. NeurIPS2020.
[9] DeeperGCN: All You Need to Train Deeper GCNs. Guohao Li et al. CoRR 2020.
[10] Natural Graph Networks. Pim de Haan et al. NeurIPS2020.
[11] Invariant and Equivariant Graph Networks. Haggai Maron et al. ICLR2019.
[12] Provably Powerful Graph Networks. Haggai Maron et al. NeurIPS2020.
[13] Coloring Graph Neural Networks for Node Disambiguation. George Dasoulas et al. IJCAI2020.
[14] Distance Encoding – Design Provably More Powerful GNNs for Structural Representation Learning. Pan Li et al. NeurIPS2020.)
[15] Identity-aware Graph Neural Networks. Jiaxuan You et al. AAAI2021.
[16] A Survey on The Expressive Power of Graph Neural Networks. Ryoma Sato et al. CoRR 2020.
[17] Building Powerful and Equivariant Graph Neural Networks with Structural Message-Passing. Clement Vignac et al. NeurIPS2020.
[18] Graph Isomorphism in Quasipolynomial Time. Laszlo Babai. STOC2016.