GAMES101作业4+反走样

声明：使用的是vs2022版，以下内容如有问题，感谢各位大佬指正！
作业要求：
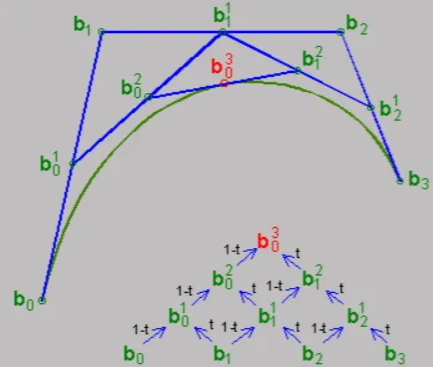
Bézier 曲线是一种用于计算机图形学的参数曲线。在本次作业中，你需要实现 de Casteljau 算法来绘制由 4 个控制点表示的 Bézier 曲线。

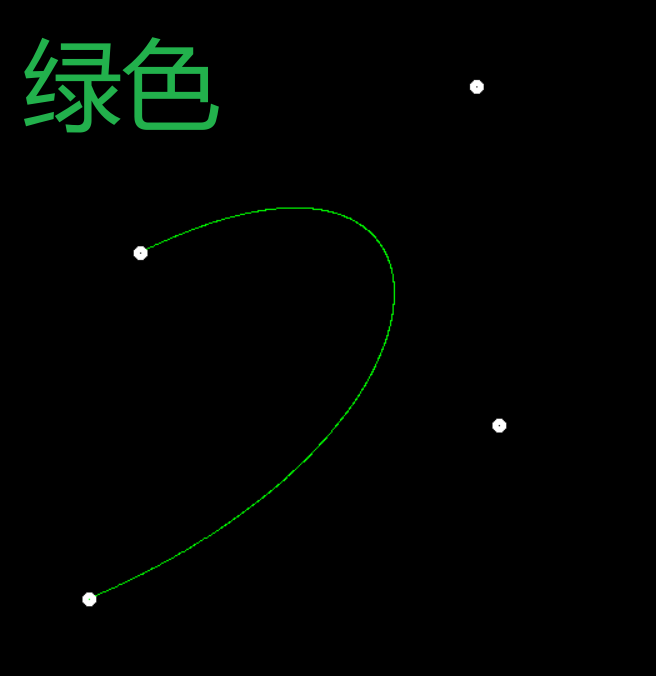
要求你的实现将 Bézier 曲线绘制为绿色。

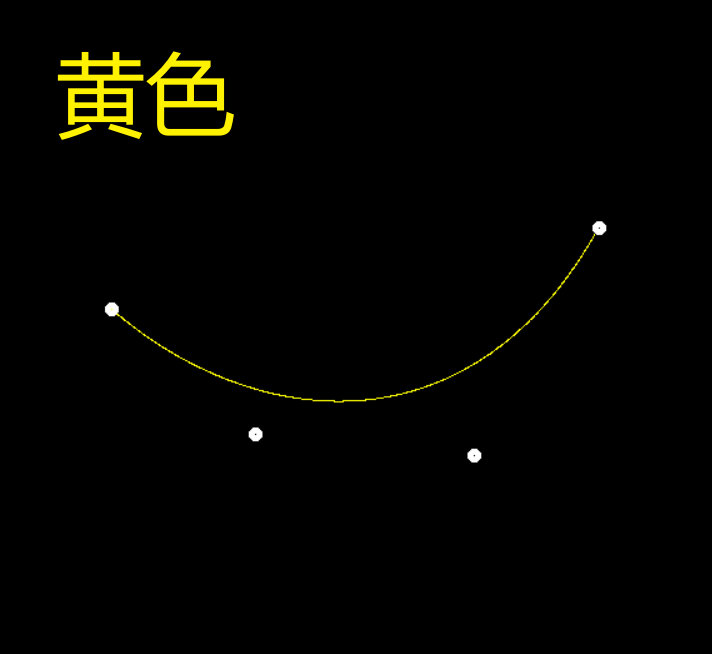
如果要确保实现正确，请同时调用 naive_bezier 和 bezier 函数，如果实现正确，则两者均应写入大致相同的像素，因此该曲线将表现为黄色。

作业效果：

💡我们需要做的：

在main.cpp中修改：

1. 函数bezier：实现绘制 Bézier 曲线的功能，使用一个控制点序列和一个OpenCV：：Mat 对象作为输入，没有返回值；使 t 在 0 到 1 的范围内进行迭代，并在每次迭代中使 t 增加一个微小值，对于需要计算的t，调用另一个函数recursive_bezier然后该函数将返回在 Bézier 曲线上 t处的点。最后，将返回的点绘制在 OpenCV ：：Mat 对象上。
2. 函数recursive_bezier：使用一个控制点序列和一个浮点数 t 作为输入，实现 de Casteljau 算法来返回 Bézier 曲线上对应点的坐标。

关键词：贝塞尔曲线；de Casteljau 算法；反走样；光栅化；加权区域采样算法

---

首先明确什么是贝塞尔曲线：
（详细推导过程可以看这篇文章：贝塞尔曲线原理、推导及Matlab实现 - zbyisgudi - 博客园）

贝塞尔曲线有如下特性：

• 通过n个控制点P1,P2,P3,...,Pn控制曲线形状。
• 曲线只经过起点P1和终点Pn.
• 对于多次贝塞尔曲线，需要引入更多的中间点

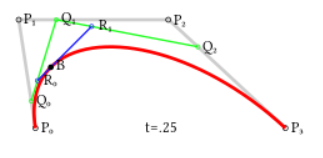
（关于贝塞尔曲线与de Casteljau 算法详细可看这篇文章：贝塞尔曲线与de Casteljau算法 - zbyisgudi - 博客园）

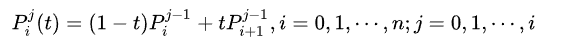
1.在main.cpp中修改bezier函数：

void bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window) 
{
    // 对 t 从 0 到 1 进行迭代，步长为 0.001
    for (double t = 0.0; t <= 1.0; t += 0.001)
    {
        // 调用 De Casteljau 递归算法计算 t 对应的曲线上的点
        cv::Point2f point = recursive_bezier(control_points, t);
        
        // 在 OpenCV 的 Mat 对象上绘制该点（绿色通道设为255，即显示为绿色）
        window.at<cv::Vec3b>(point.y, point.x)[1] = 255;
    }
}

2.在main.cpp中修改recursive_bezier函数：

cv::Point2f recursive_bezier(const std::vector<cv::Point2f> &control_points, float t) 
{
    // TODO: Implement de Casteljau's algorithm

    // 终止条件：当控制点序列只剩一个点时，直接返回该点
    if (control_points.size() == 1)
        return control_points[0];

    // 创建新的控制点序列，用于存储本轮递归生成的中间点
    std::vector<cv::Point2f> next_control_points = {};

    // 遍历当前控制点序列，按 t:(1-t) 比例生成新的中间点
    for (int i = 0; i < control_points.size() - 1; i++)
    {
        auto& a = control_points[i];      // 当前线段的起点
        auto& b = control_points[i + 1];  // 当前线段的终点

        // 按 t:(1-t) 比例计算分割点：p = a + t*(b-a) = (1-t)*a + t*b
        auto p = a + t * (b - a);

        // 将新生成的中间点添加到下一轮控制点序列中
        next_control_points.push_back(p);
    }

    // 递归调用，继续处理新生成的控制点序列
    return recursive_bezier(next_control_points, t);
}    

//在int main中的while循环中调用naive_bezier(control_points, window);
if (control_points.size() == 4) 
{
    //调用naive_bezier，结果是红色
    naive_bezier(control_points, window);
    //bezier(control_points, window);
    

    cv::imshow("Bezier Curve", window);
    cv::imwrite("my_bezier_curve.png", window);
    key = cv::waitKey(0);

    return 0;
}

//在int main中的while循环中调用bezier(control_points, window);
if (control_points.size() == 4) 
{
    //naive_bezier(control_points, window);
    bezier(control_points, window);
    //调用bezier，结果是绿色

    cv::imshow("Bezier Curve", window);
    cv::imwrite("my_bezier_curve.png", window);
    key = cv::waitKey(0);

    return 0;
}

//在int main中的while循环中调用bezier(control_points, window);
if (control_points.size() == 4) 
{
    naive_bezier(control_points, window);
    bezier(control_points, window);
    //如果同时调用naive_bezier和bezier，结果是黄色

    cv::imshow("Bezier Curve", window);
    cv::imwrite("my_bezier_curve.png", window);
    key = cv::waitKey(0);

    return 0;
}

---

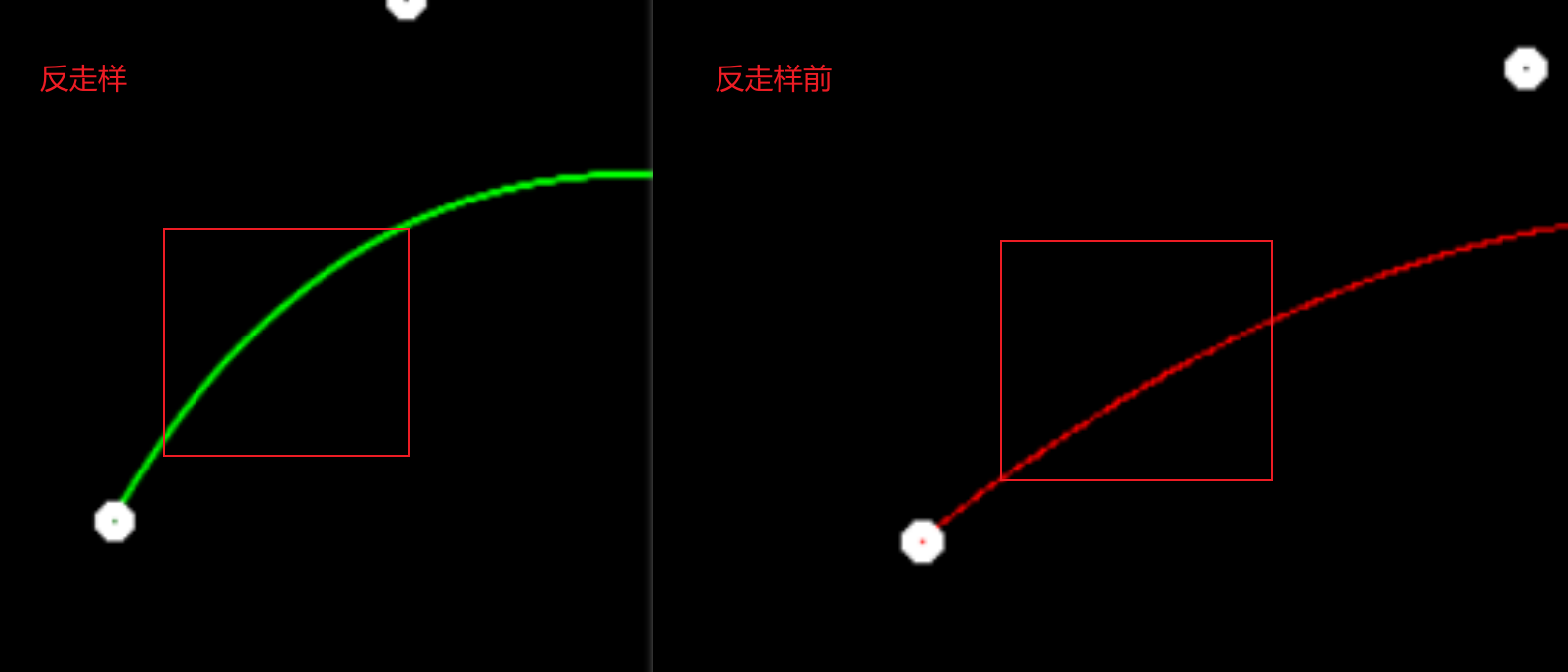
【提高项】：

反走样：加权区域采样方法，选取像素点四周的区域，根据相交区域与像素中心的距离来决定其对象亮度的贡献

void bezier(const std::vector<cv::Point2f>& control_points, cv::Mat& window)
{
    // TODO: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's 
    // recursive Bezier algorithm.

    // 遍历参数t从0到1，步长0.001
    for (double t = 0.0; t <= 1.0; t += 0.001)
    {
        // 1. 计算Bezier曲线上参数t对应的点（点计算）
        cv::Point2f p = recursive_bezier(control_points, t);

        // 2. 确定最接近p的整数坐标点p0（四舍五入）
        cv::Point2i p0(p.x - std::floor(p.x) < 0.5 ? std::floor(p.x) : std::ceil(p.x),
            p.y - std::floor(p.y) < 0.5 ? std::floor(p.y) : std::ceil(p.y));

        // 3. 离p最近的整数坐标点p0及其左、上、左上三个相邻点，形成2×2的像素网格
        std::vector<cv::Point2i> ps = { p0,
                                       cv::Point2i(p0.x - 1, p0.y),
                                       cv::Point2i(p0.x, p0.y - 1),
                                       cv::Point2i(p0.x - 1, p0.y - 1) };

        // 4. 计算p到各像素中心点的距离权重
        float sum_d = 0.f;                // 总权重
        float max_d = sqrt(2);            // 最大距离（对角线长度）
        std::vector<float> ds = {};       // 存储各点权重

        for (int i = 0; i < 4; i++) {
            // 计算像素中心点坐标（像素中心为x+0.5, y+0.5）
            cv::Point2f cp(ps[i].x + 0.5f, ps[i].y + 0.5f);

            // 距离越远，权重越小（max_d-实际距离）
            float d = max_d - std::sqrt(std::pow(p.x - cp.x, 2) + std::pow(p.y - cp.y, 2));
            ds.push_back(d);
            sum_d += d;
        }

        // 5. 基于距离权重，对四个像素进行颜色叠加（抗锯齿核心）
        for (int i = 0; i < 4; i++) {
            // 归一化权重（总和为1）
            float k = ds[i] / sum_d;

            // 获取像素原有绿色值（OpenCV中BGR顺序，1对应G通道）
            uchar& green = window.at<cv::Vec3b>(ps[i].y, ps[i].x)[1];

            // 叠加颜色：原绿色值 + 255×权重（上限255）
            green = std::min(255.f, green + 255.f * k);
        }
    }
}

//然后在int main中的while循环中调用bezier(control_points, window);
if (control_points.size() == 4) 
{
    //naive_bezier(control_points, window);
    bezier(control_points, window);
    //调用bezier，采用反走样

    cv::imshow("Bezier Curve", window);
    cv::imwrite("my_bezier_curve.png", window);
    key = cv::waitKey(0);

    return 0;
}