GAMES101作业1

声明：使用的是vs2022版，以下内容如有问题，感谢各位大佬指正！
作业要求：

作业目的：模拟一个基于 CPU 的光栅化渲染器的简化版本

我们需要做的：

💡在main.cpp中修改

1. Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,float zNear, float zFar)//给定参数创建一个模型变换矩阵（一个在3维中绕z轴旋转的变换矩阵）
2. Eigen::Matrix4f get_model_matrix(float rotation_angle)//(一个透视投影矩阵）

关键词：模型、视图、投影矩阵；旋转矩阵；透视投影矩阵；屏幕坐标

1.一个在3维中绕z轴旋转的变换矩阵

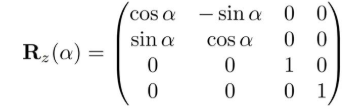
Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
    Eigen::Matrix4f model = Eigen::Matrix4f::Identity();

    // TODO: Implement this function
    // Create the model matrix for rotating the triangle around the Z axis.
    // Then return it.

    //旋转矩阵
    float a = rotation_angle / 180.0 * MY_PI;
    //传入的角度参数是使用角度制表示，而std三角函数接收弧度制，因此要做一个转换
    
    model << cos(a), -sin(a), 0, 0,
        sin(a), cos(a), 0, 0,
        0, 0, 1, 0,
        0, 0, 0, 1;

    return model;
}

2.一个透视投影矩阵

分两步：

1.透视转正交

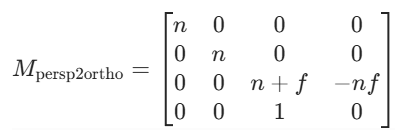
2.正交映射正则立方体中

Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,float zNear, float zFar)
{
    // Students will implement this function
    Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();
    // TODO: Implement this function
    // Create the projection matrix for the given parameters.
    // Then return it.

    //透视矩阵先要转换为正交，然后转到正则立方体
    // 1. 透视投影转为正交投影矩阵
    float n = zNear;
    float f = zFar;
    Eigen::Matrix4f M_persp2Ortho;
    M_persp2Ortho << n, 0, 0, 0,
        0, n, 0, 0,
        0, 0, n + f, -n * f,
        0, 0, 1, 0;

    //对应关系
    //由于采用的是右手坐标系，相机朝着 - z 方向，所以t是负数，这样可以保证渲染出的图像方向是正确的。
    float fov = eye_fov * MY_PI / 180.0;
    float t = -n * tan(fov / 2.);//解决原三角倒着的方法，将t换为-t，所以在等式右边加负号
    // 近平面上边缘的y坐标
    
    float b = -t;// 近平面下边缘的y坐标（与上边缘对称）
    float r = aspect_ratio * t;// 近平面右边缘的x坐标，aspect_ratio宽高比
    float l = -r;// 近平面左边缘的x坐标
    
    //转正则立方体
    Eigen::Matrix4f M_ortho, trans, scale;
    
    // 平移矩阵：将中心移至原点
    trans << 1, 0, 0, -(r + l) / 2,
        0, 1, 0, -(t + b) / 2,
        0, 0, 1, -(n + f) / 2,
        0, 0, 0, 1;
        
    // 缩放矩阵：将长方体缩放为正则立方体
    scale << 2 / (r - l), 0, 0, 0,
        0, 2 / (t - b), 0, 0,
        0, 0, 2 / (n - f), 0,
        0, 0, 0, 1;
        
    // 正交投影矩阵 = 缩放矩阵 × 平移矩阵
    M_ortho = scale * trans;
    
    //最终投影矩阵的合成
    //矩阵相乘的顺序是从右到左，也就是先进行透视到正交的转换，再进行正交规范化处理。
    projection = M_ortho * M_persp2Ortho;
    return projection;
}

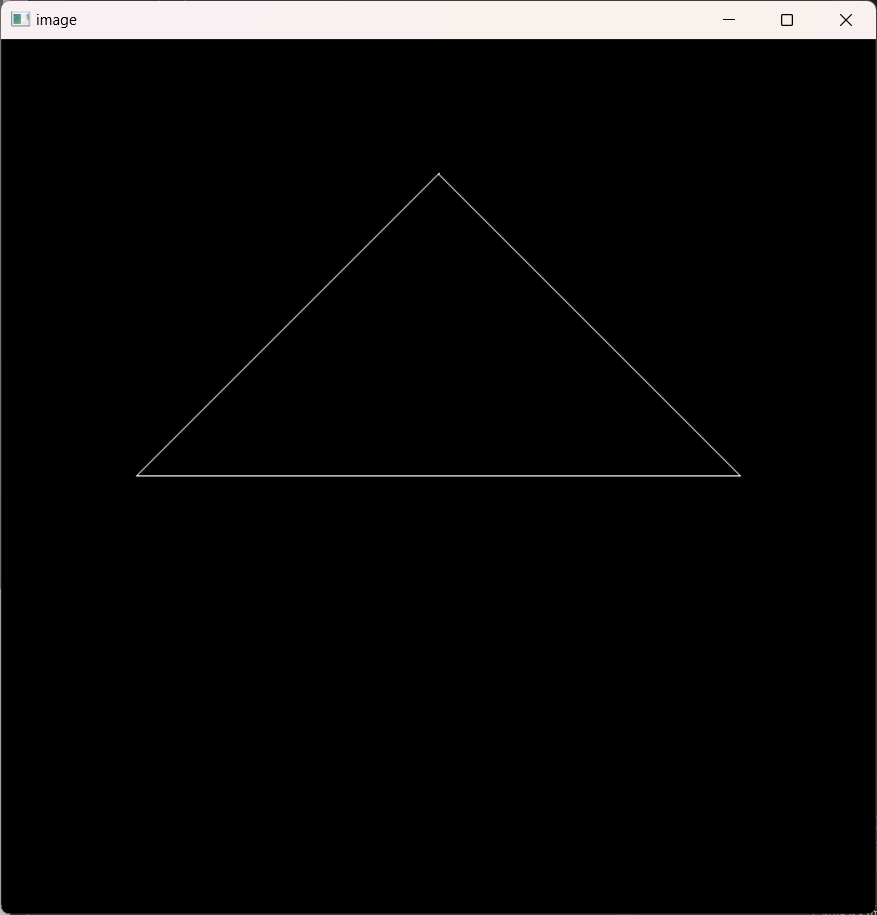
最后运行，得到这幅图，按AD可以左右旋转