pytorch深度学习实战:从线性模型到神经网络
本文将合集上一篇文章的代码继续盖章。在本文第一节，解释了神经元、神经网络、激活函数以及为什么线性模型+激活函数能够模拟任意函数。接着在第二节，通过torch.nn模块，改造代码，实现了线性模型。接着在第四节，加入激活函数，并构造了一个简单的全链接神经网络，并说明了如何查看神经网络的参数。最后一届，展示了本文的实验结果和完整代码。
一、神经网络
1.1 神经元和神经网络
一个神经元o = 线性变化 + 非线性函数。
从数学上讲，我们可以把它写成 o = f(wx + b)，其中 x 是输入，w 是权重或比例因子，b 是偏置或偏移量，f 是激活函数，设为双曲正切，这里是 tanh 函数。
通常，x 和 o 可以是简单的标量，或向量值（意思是保留许多标量值）。类似地，w 可以是单个标量或矩阵，而 b 是标量或向量（输入的维度和权重必须匹配）。在后一种情况下，前面的表达式被称为一层神经元，因为它通过多维权重和偏置来表示许多神经元。
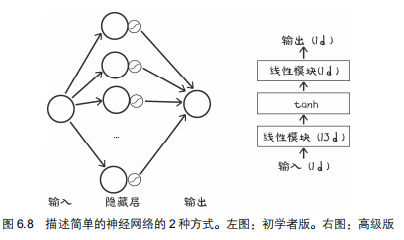
一个神经元：
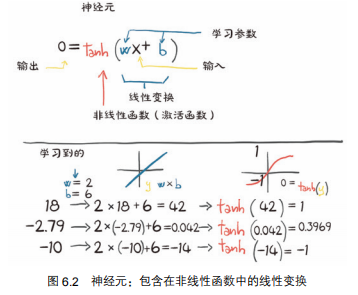
一层神经元：
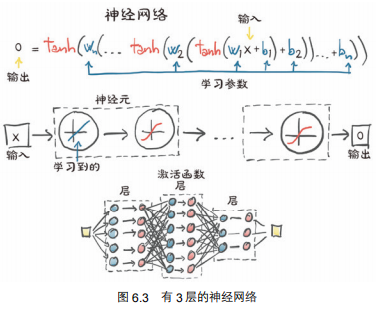
1.2 非线性的激活函数
激活函数的重要作用：
-
近似任意函数
-
将输出集中到给定的范围：
- 限制输出范围，压缩输出范围；
- 当在敏感范围时，输入的微小改变将导致结果的显著变化。如下图6.4
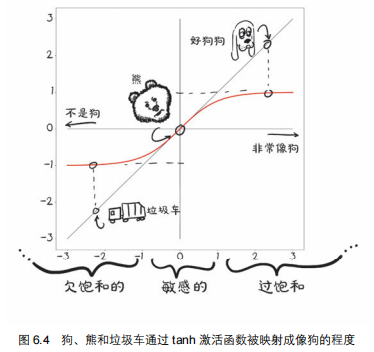
更多的激活函数
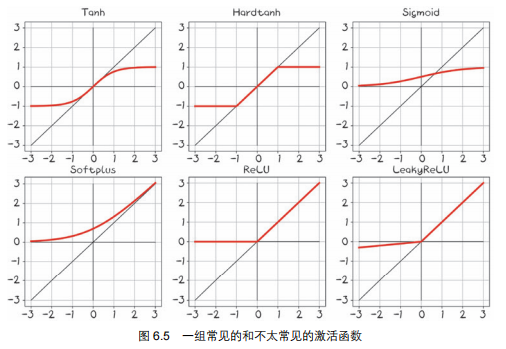
通过线性方程+激活函数得到各种各样函数
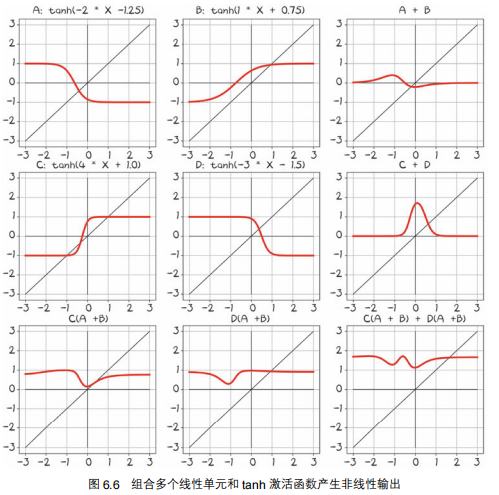
通过图6.6，我们得到这样的理解：
让我们进一步了解学习的机制：深度神经网络使我们能够在没有明确模型的情况下近似处理高度非线性的问题。相反，从一个通用的、未经训练的模型开始，我们通过为它提供一组输入和输出以及一个可以反向传播的损失函数，使它专门处理某项任务。使用样本将一个通用模型专门化为一个任务就是我们所说的学习。
随着多输入和多输出，输入输出关系变得复杂。物理学家或应用数学家的工作往往是从第一原理出发，对一种现象进行功能性描述，然后从测量中估计未知的参数，从而得到一个精确的、真实世界的模型。另一方面，深度神经网络是一组函数，能够近似出大范围的输入输出关系，而不需要我们对某一现象构建解释模型。在某种程度上，我们放弃解释，以换取解决日益复杂的问题的可能性。换句话说，我们有时缺乏能力、信息或计算资源来为我们所呈现的事物建立一个明确的模型，所以数据驱动是我们前进的唯一途径。
二、线性模型
我们继续在pytorch深度学习实战:线性模型上的学习的最终代码上应用nn.Module，做主要涉及模型和损失函数的修改。修改内容如下：
2.1 torch.nn的三个注意事项
-
块必须是顶级属性，而不是隐藏在列表或 dict 实例中则，优化器将无法定位子模块以及它们的参数。对于模型需要一列或一组子模块的情况，Torch 提供了 nn.ModuleList 和 nn.ModuleDict
-
使用__call__()，而不是forward()
使用一组参数调用 nn.Module 的实例，最后使用相同的参数调用名为 forward 的方法。forward()方法执行前向计算，call()方法在调用 forward()之前和之后执行其他重要的事情。因此，直接调用 forward()方法在技术上是可行的，它将与__call__()方法产生相同的输出，但不能在用户编码中这样做：
y = model(x) # 正确 y = model.forward(x) # 不能这么干！ -
nn模块的所有层都默认处理批量数据，即第0维是batch size，输入张量大小为 B x N_in。
其中，B为批次的大小，N_in为输入特征的数量。即行中有样本，列中有特征。样本1 [特征1_1，特征1_2，...,特征1_n] 样本2 [特征2_1，特征2_2，...,特征2_n] ... 样本n [特征n_1，特征n_2，...,特征n_n]
2.2 使用线性模型拟合数据(nn.Linear())
2.2.1 数据处理
重塑维度 B -> B x N_in
torch.Size([11]) -> torch.Size([11, 1])
t_c = torch.tensor(t_c).unsqueeze(1) # B x N_in, nn的第一维(行)必须是batch size; 即行中有样本，列中有特征
t_u = torch.tensor(t_u).unsqueeze(1)
2.2.2 更新模型
# 模型
linear_model = nn.Linear(1, 1) # 输入特征数为1，输出特征数为1
2.2.3 更新优化器
# 优化器
learning_rate = 1e-2
optimizer = optim.SGD(linear_model.parameters(), lr = learning_rate)
其中，我们使用parameters()方法来访问任何 nn.Module 或它的子模块拥有的参数列表
>>> linear_model = torch.nn.Linear(1, 1)
>>> list(linear_model.parameters())
[Parameter containing:
tensor([[-0.9341]], requires_grad=True), Parameter containing:
tensor([0.5041], requires_grad=True)]
2.2.4 更新训练代码
# 循环训练
def training_loop(n_epochs, optimizer, model, loss_fn, train_t_u, train_t_c, val_t_u, val_t_c):
for epoch in range(1, n_epochs + 1):
train_t_p = model(train_t_u)
train_loss = loss_fn(train_t_p, train_t_c)
with torch.no_grad():
val_t_p = model(val_t_u)
val_loss = loss_fn(val_t_p, val_t_c)
optimizer.zero_grad()
train_loss.backward()
optimizer.step()
if epoch <=3 or epoch % 500 == 0:
print('Epoch %d, Train Loss %f.4, Val Loss %f.4' % (epoch, float(train_loss), float(val_loss)))
# -----------------------------------------------------------------------
training_loop(
n_epochs = 4000,
optimizer = optimizer,
model = linear_model,
loss_fn = nn.MSELoss(), # 我们将不再使用自定义的损失函数
train_t_u = train_t_un,
train_t_c = train_t_c,
val_t_u = val_t_un,
val_t_c = val_t_c)
print()
print(linear_model.weight)
print(linear_model.bias)
2.3 完整代码
点击查看代码
'''
用传统方法训练华氏度和摄氏度的转换函数
线性模型
'''
import torch
import torch.optim as optim
import torch.nn as nn
# -----------------------------------------------------------------------
# 原始数据
t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
t_c = torch.tensor(t_c).unsqueeze(1) # B x N_in, nn的第一维(行)必须是batch size; 即行中有样本，列中有特征
t_u = torch.tensor(t_u).unsqueeze(1)
t_un = 0.1 * t_u # 归一化处理
# -----------------------------------------------------------------------
# 分割数据集
n_samples = t_u.shape[0]
n_val = int(0.2 * n_samples)
shuffled_indices = torch.randperm(n_samples)
train_indices = shuffled_indices[:-n_val]
val_indices = shuffled_indices[-n_val:]
train_t_u = t_u[train_indices]
train_t_c = t_c[train_indices]
val_t_u = t_u[val_indices]
val_t_c = t_c[val_indices]
train_t_un = 0.1 * train_t_u # 归一化
val_t_un = 0.1 * val_t_u
# -----------------------------------------------------------------------
# 模型
linear_model = nn.Linear(1, 1) # 输入特征数为1，输出特征数为1
# 优化器
learning_rate = 1e-2
optimizer = optim.SGD(linear_model.parameters(), lr = learning_rate)
# 循环训练
def training_loop(n_epochs, optimizer, model, loss_fn, train_t_u, train_t_c, val_t_u, val_t_c):
for epoch in range(1, n_epochs + 1):
train_t_p = model(train_t_u)
train_loss = loss_fn(train_t_p, train_t_c)
with torch.no_grad():
val_t_p = model(val_t_u)
val_loss = loss_fn(val_t_p, val_t_c)
optimizer.zero_grad()
train_loss.backward()
optimizer.step()
if epoch <=3 or epoch % 500 == 0:
print('Epoch %d, Train Loss %f.4, Val Loss %f.4' % (epoch, float(train_loss), float(val_loss)))
# -----------------------------------------------------------------------
training_loop(
n_epochs = 4000,
optimizer = optimizer,
model = linear_model,
loss_fn = nn.MSELoss(), # 我们将不再使用自定义的损失函数
train_t_u = train_t_un,
train_t_c = train_t_c,
val_t_u = val_t_un,
val_t_c = val_t_c)
print()
print(linear_model.weight)
print(linear_model.bias)
# -----------------------------------------------------------------------
# 可视化数据
import matplotlib.pyplot as plt
t_p = linear_model(t_un)
# fig = plt.figure(dpi = 600)
plt.plot(t_u.numpy(), t_p.detach().numpy())
plt.plot(t_u.numpy(), t_c.numpy(), 'o')
plt.xlabel('Temperature (°Fahrenheit)')
plt.ylabel('Temperature (°Celsius)')
plt.legend(['Prediction', 'Observation'])
plt.show()
三、完成神经网络
3.1 将线性模型变成简单的神经网络
# 模型
seq_model = nn.Sequential(
nn.Linear(1, 13), # 输入特征数为1，输出特征数为13
nn.Tanh(),
nn.Linear(13, 1) # 输入特征数为13，输出特征数为1
)
则，神经网络的形状如下：
>>> seq_model
Sequential(
(0): Linear(in_features=1, out_features=10, bias=True)
(1): Tanh()
(2): Linear(in_features=10, out_features=1, bias=True)
)
3.2 检查神经网络参数的方法
3.2.1 检查参数
parameters简单检查参数
list(seq_model.parameters())
输出
点击查看代码
[Parameter containing:
tensor([[ 0.4222],
[ 0.0990],
[ 0.6049],
[ 0.4690],
[-0.8505],
[-0.8519],
[-0.3656],
[ 0.9970],
[ 0.5956],
[-0.5648],
[ 0.2347],
[ 0.4646],
[ 0.8371]], requires_grad=True), Parameter containing:
tensor([ 0.8554, 0.0699, -0.3446, -0.3757, -0.4206, 0.4170, 0.1826, -0.7581,
0.7537, -0.2010, 0.0931, -0.6027, 0.7324], requires_grad=True), Parameter containing:
tensor([[ 0.0884, 0.2263, 0.0552, 0.0277, 0.0143, -0.0371, -0.1932, -0.2586,
-0.1834, -0.0583, 0.1592, -0.0412, -0.2679]], requires_grad=True), Parameter containing:
tensor([0.2411], requires_grad=True)]
检查参数形状
print([param.shape for param in seq_model.parameters()])
输出
[torch.Size([13, 1]), torch.Size([13]), torch.Size([1, 13]), torch.Size([1])]
torch.Size([13, 1])代表13个神经元，每个神经元1个特征
torch.Size([13])代表13个偏置
3.2.2 命名每个模块
自动命名
seq_model = nn.Sequential(
nn.Linear(1, 13), # 输入特征数为1，输出特征数为13
nn.Tanh(),
nn.Linear(13, 1) # 输入特征数为13，输出特征数为1
)
# 获得名称
for name, param in seq_model.named_parameters():
print(name, param.shape)
输出：
0.weight torch.Size([13, 1])
0.bias torch.Size([13])
2.weight torch.Size([1, 13])
2.bias torch.Size([1])
手动命名
from collections import OrderedDict
seq_model = nn.Sequential(OrderedDict([
('hidden_linear', nn.Linear(1, 13)),
('hidden_activation', nn.Tanh()),
('output_linear', nn.Linear(13, 1))
]))
获得解释性名称
for name, param in seq_model.named_parameters():
print(name, param.shape)
# 输出
# hidden_linear.weight torch.Size([13, 1])
# hidden_linear.bias torch.Size([13])
# output_linear.weight torch.Size([1, 13])
# output_linear.bias torch.Size([1])
将子模块作为属性来访问特定的参数，例：
print(seq_model.hidden_linear.bias)
print(seq_model.hidden_linear.weight.grad)
四、本文最终代码
点击查看代码
'''
用传统方法训练华氏度和摄氏度的转换函数
完成一个神经网络
'''
import torch
import torch.optim as optim
import torch.nn as nn
# -----------------------------------------------------------------------
# 原始数据
t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
t_c = torch.tensor(t_c).unsqueeze(1) # B x N_in, nn的第一维(行)必须是batch size; 即行中有样本，列中有特征
t_u = torch.tensor(t_u).unsqueeze(1)
# t_un = 0.1 * t_u # 归一化处理
# -----------------------------------------------------------------------
# 分割数据集
n_samples = t_u.shape[0]
n_val = int(0.2 * n_samples)
shuffled_indices = torch.randperm(n_samples)
train_indices = shuffled_indices[:-n_val]
val_indices = shuffled_indices[-n_val:]
train_t_u = t_u[train_indices]
train_t_c = t_c[train_indices]
val_t_u = t_u[val_indices]
val_t_c = t_c[val_indices]
train_t_un = 0.1 * train_t_u # 归一化
val_t_un = 0.1 * val_t_u
# -----------------------------------------------------------------------
# 模型
seq_model = nn.Sequential(
nn.Linear(1, 13), # 输入特征数为1，输出特征数为13
nn.Tanh(),
nn.Linear(13, 1) # 输入特征数为13，输出特征数为1
)
# 优化器
learning_rate = 1e-3
optimizer = optim.SGD(seq_model.parameters(), lr = learning_rate)
# 循环训练
def training_loop(n_epochs, optimizer, model, loss_fn, train_t_u, train_t_c, val_t_u, val_t_c):
for epoch in range(1, n_epochs + 1):
train_t_p = model(train_t_u)
train_loss = loss_fn(train_t_p, train_t_c)
with torch.no_grad():
val_t_p = model(val_t_u)
val_loss = loss_fn(val_t_p, val_t_c)
optimizer.zero_grad()
train_loss.backward()
optimizer.step()
if epoch <=3 or epoch % 500 == 0:
print('Epoch %d, Train Loss %f.4, Val Loss %f.4' % (epoch, float(train_loss), float(val_loss)))
# -----------------------------------------------------------------------
training_loop(
n_epochs = 5000,
optimizer = optimizer,
model = seq_model,
loss_fn = nn.MSELoss(), # 我们将不再使用自定义的损失函数
train_t_u = train_t_un,
train_t_c = train_t_c,
val_t_u = val_t_un,
val_t_c = val_t_c)
print('output', seq_model(val_t_un))
print('answer', val_t_c)
# -----------------------------------------------------------------------
# 可视化数据
import matplotlib.pyplot as plt
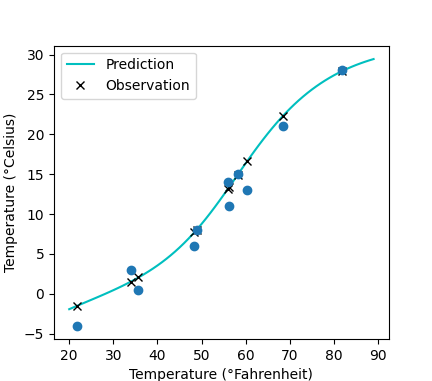
t_range = torch.arange(20., 90.).unsqueeze(1)
plt.plot(t_range.numpy(), seq_model(0.1 * t_range).detach().numpy(), 'c-')
plt.plot(t_u.numpy(), seq_model(0.1 * t_u).detach().numpy(), 'kx')
# plt.plot(t_u.numpy(), t_p.detach().numpy())
plt.plot(t_u.numpy(), t_c.numpy(), 'o')
plt.xlabel('Temperature (°Fahrenheit)')
plt.ylabel('Temperature (°Celsius)')
plt.legend(['Prediction', 'Observation'])
plt.show()
浙公网安备 33010602011771号