【高中数学/解析几何/椭圆】设椭圆C：x^2/a^2+y^2/b^2=1(a>b>0)的焦点为F1、F2，P是椭圆上的一点，且∠F1PF2=60°，若▲F1PF2的外接圆和内切圆的半径分别为R、r，当R=3r时，椭圆的离心率为多少？

【问题】

设椭圆C：x^2/a^2+y^2/b^2=1(a>b>0)的焦点为F1、F2，P是椭圆上的一点，且∠F1PF2=60°，若▲F1PF2的外接圆和内切圆的半径分别为R、r，当R=3r时，椭圆的离心率为多少？

A.1/2

B.3/5

C.4/5

D.三分之根号五

【答案】

B

【解答】

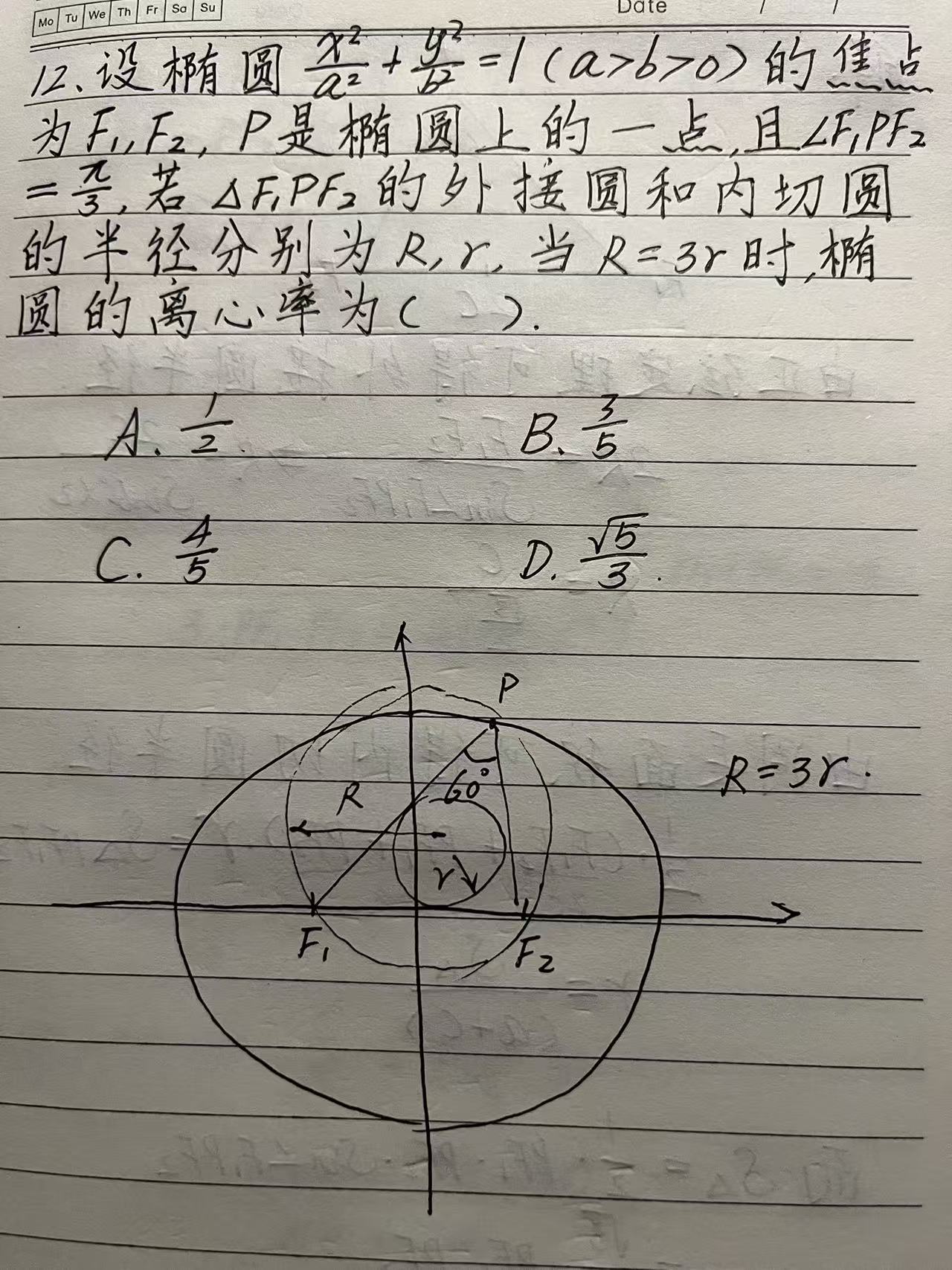
【点评】

一道题集中了椭圆的特性和三角形的正弦、余弦、周长、面积，知识点密集且需要洞察力，是道经典题。

END