【高中数学/椭圆】已知动圆C与圆C1：（x-1）^2+y^2=9内切，同时与圆C2：（x+1)^2+y^2=1外切，圆心C的轨迹为E，斜率为K的动直线与轨迹E相交于不同的两点A和B。 求（1）轨迹E的方程（2）若AB中点的横坐标为1，求S▲OAB最大值，并求此时K的值（3）若以AB为直径的圆经过P(1,1.5),求证L过定点，并求定点之坐标。

【问题】

19.已知动圆C与圆C1：（x-1）^2+y^2=9内切，同时与圆C2：（x+1)^2+y^2=1外切，圆心C的轨迹为E，斜率为K的动直线与轨迹E相交于不同的两点A和B。

求（1）轨迹E的方程（2）若AB中点的横坐标为1，求S▲OAB最大值，并求此时K的值（3）若以AB为直径的圆经过P(1,1.5),求证L过定点，并求定点之坐标。

【答案】

x^2/4+y^2/3=1;

S▲OAB最大值=根号三，k去±二分之根号三；

（略）

【出处】

2026年1月14日大连二十四中高二上数学期末卷 第19题 压轴题 17分

【解答】

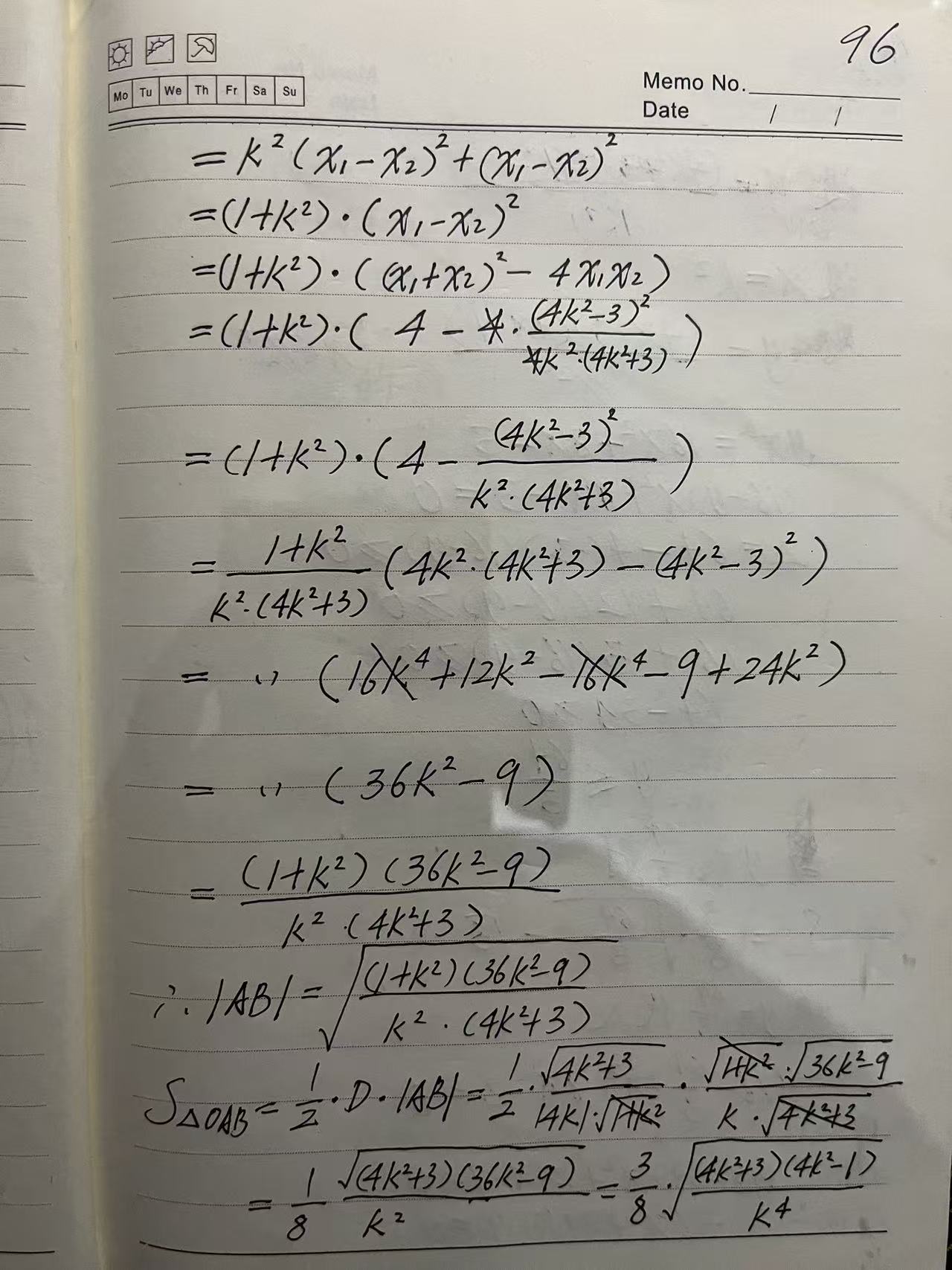
【点评】

第二三问计算量都不小，挺难为考场上的孩子们的。

END