【高中数学/立体几何/直线与面】空间直角坐标系中，平面Ω和方程┏：Ax+By+Cz+D=0(ABC不同时为零)之间具有如下关系： （1）平面Ω上的点的坐标都是┏的解； （2）以方程┏的解为坐标的点都在平面Ω上。 则称平面Ω为方程┏的平面，方程┏为Ω的方程，并且称n=（A,B,C)为平面Ω的一个法向量。 已知平面Ω1，Ω2方程分别为T1：2x-y+z-1=0和T2：x+y-2z=0,平...

【问题】

11.空间直角坐标系中，平面Ω和方程┏：Ax+By+Cz+D=0(ABC不同时为零)之间具有如下关系：

（1）平面Ω上的点的坐标都是┏的解；

（2）以方程┏的解为坐标的点都在平面Ω上。

则称平面Ω为方程┏的平面，方程┏为Ω的方程，并且称n=（A,B,C)为平面Ω的一个法向量。

已知平面Ω1，Ω2方程分别为T1：2x-y+z-1=0和T2：x+y-2z=0,平面Ω1，Ω1的交线为l，则（    ）

A.r若点A(1,m,n)在直线l上，则m=3，n=2.

B.平面Ω1，Ω1所成角的余弦值为-1/6

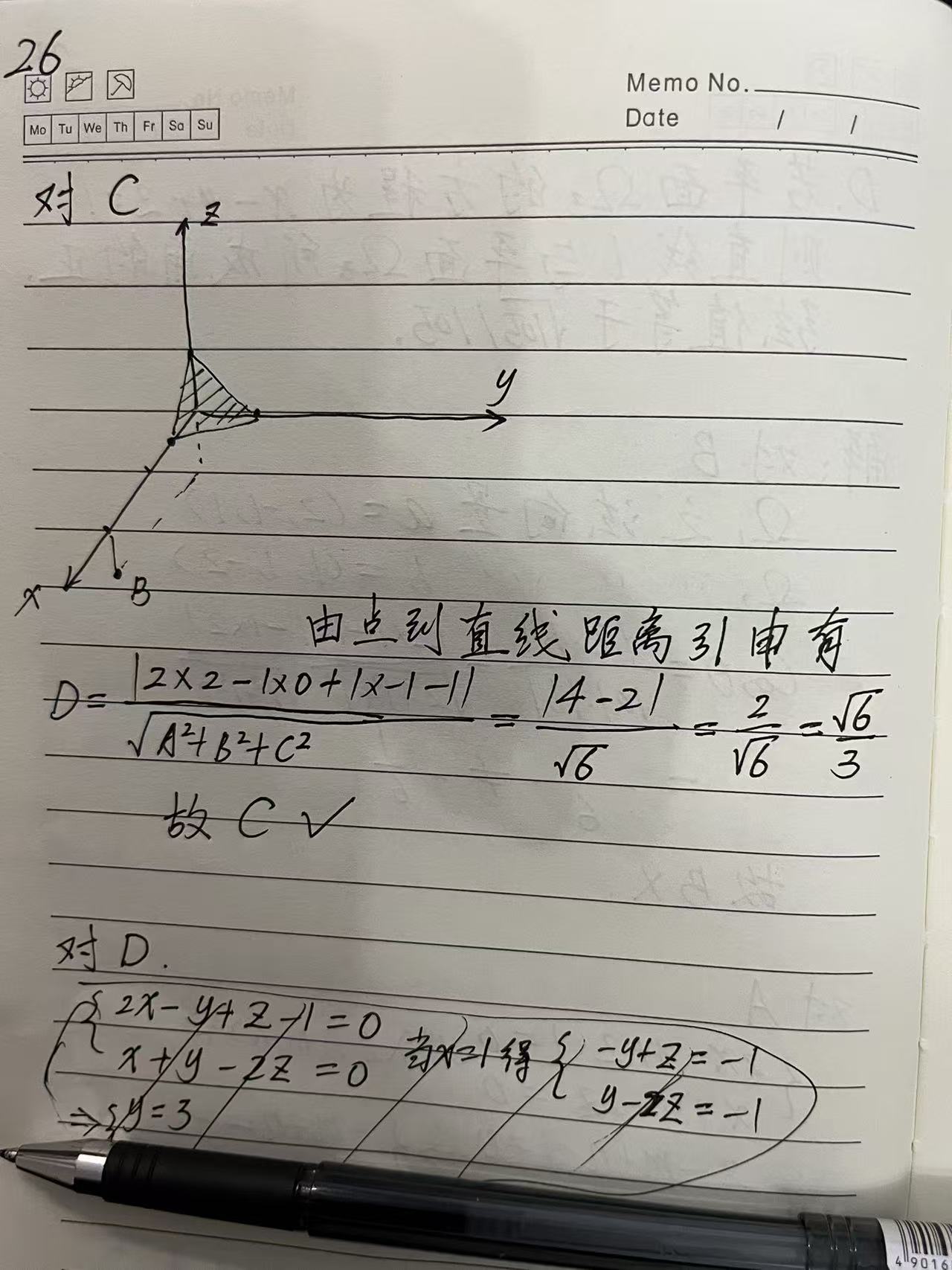
C.点（2，0，-1）到Ω1的距离为根号六/3

D.若平面Ω3的方程为x-y+z=1,则直线l与平面Ω3所成角的正弦值等于1/根号下105.

 

【答案】

ACD

【出处】

2026年1月14日大连二十四中高二上数学期末卷 第11题 多选题最后一道

【解答】

【点评】

概念题，就怕记不住，记住了是送分。

END