大学微积分 AB 第七单元：微分方程（微分方程简介、可分离方程简介、解决代数处理微分的问题）

微积分的关系

微积分的基本定理将微分与积分联系起来，表明在某种意义上，微分和积分是互为反操作的。具体而言：

• 若你首先对一个函数进行积分（求其原函数），然后对这个原函数进行微分，那么你会得到最初的函数。
• 反之亦然，若你对一个函数进行微分然后进行积分，你将得到相同的结果（加上常数项）。

因此，微积分不仅包括导数的求取，也涉及对函数的累积与总和，二者相辅相成。

 

 

微分方程简介

微分在数学中通常指的是求导。具体来说，微分是研究函数变化率的工具，导数表示函数在某一点的瞬时变化率。

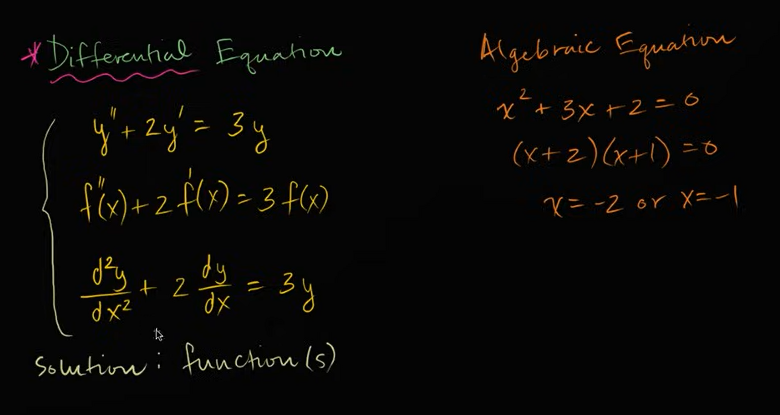
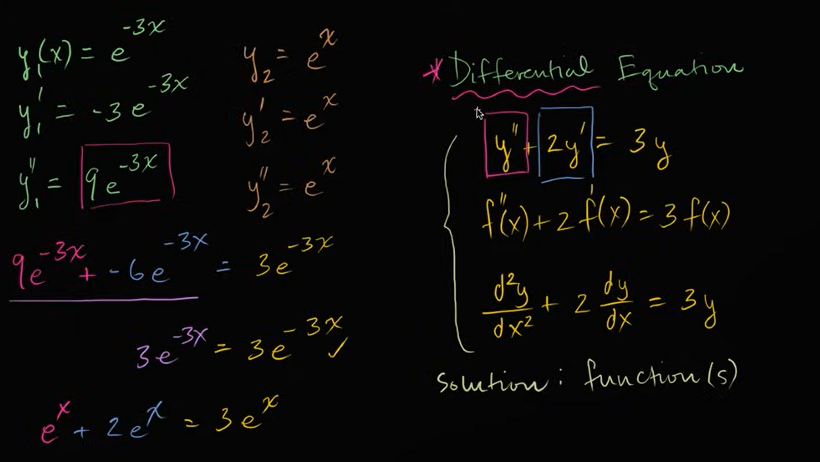
 例子：

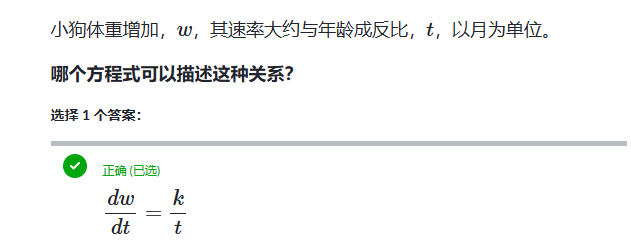
 例子：

 

验证微分方程的解

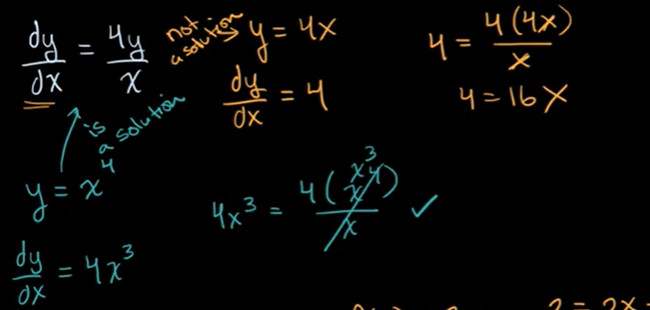
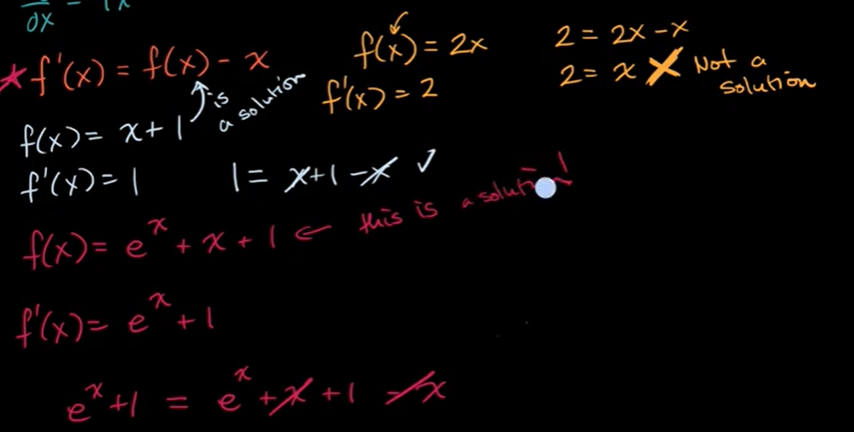
 例子：

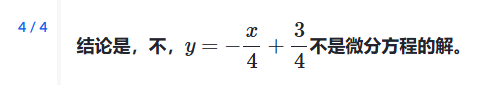
 例子：

 

 例子：

 

 

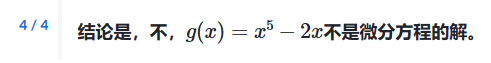
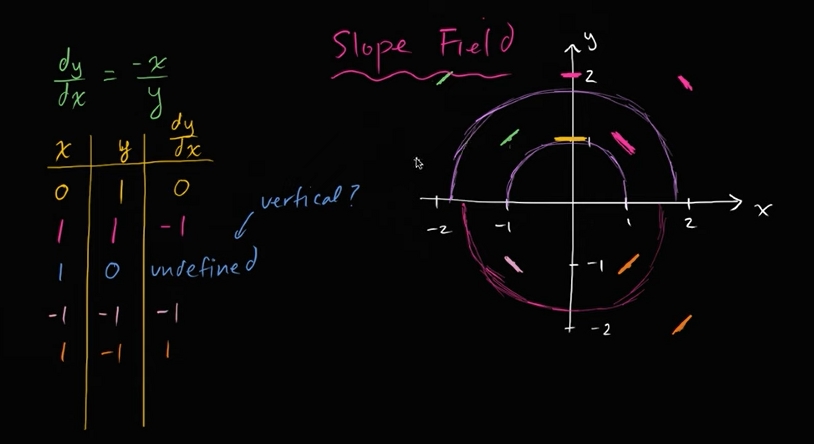
坡地介绍

 

可分离方程简介

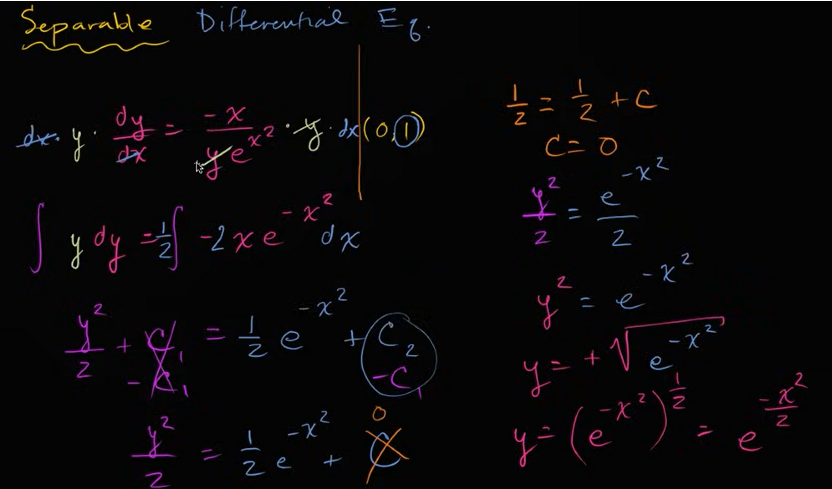
 例子：

 

 

 

 

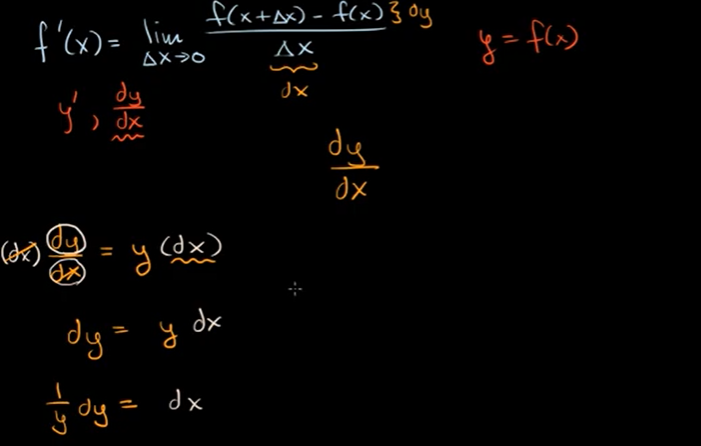
 例子：

 

 

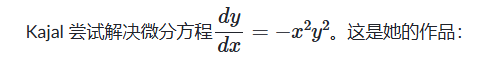
例子：可分离微分方程

 例子：

 

 例子：

 

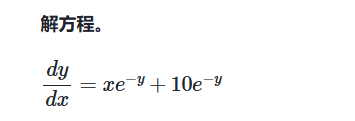
 例子：

 

 例子：

 

 

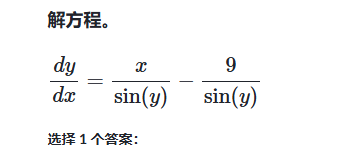
示例：识别可分离方程

 

 

识别可分离方程

 

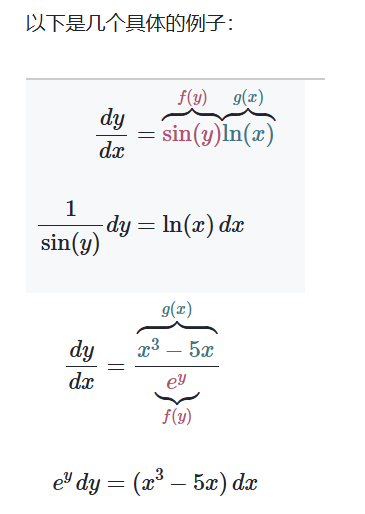
 例子：

 

微分方程的特殊解：有理函数

 

微分方程的特殊解：指数函数

 

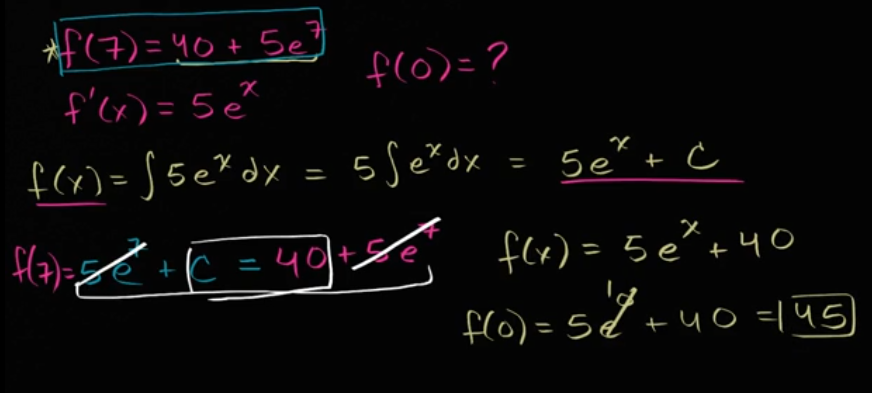
例子：

 例子：

 

示例：寻找可分离方程的具体解

 

例子：具有隐式解的可分离方程

 例子：

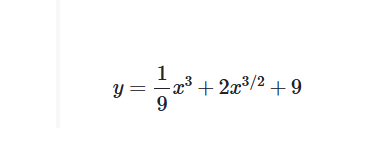
 例子：