大学微积分 AB 第 5 单元-1：应用导数分析函数 (中值定理、极值定理、寻找关键点、临界点、最小点和最大点简介、在闭区间内寻找绝对极值)（凹度介绍、拐点介绍、分析凹度（代数）、拐点（代数）、二阶导数检验）

 

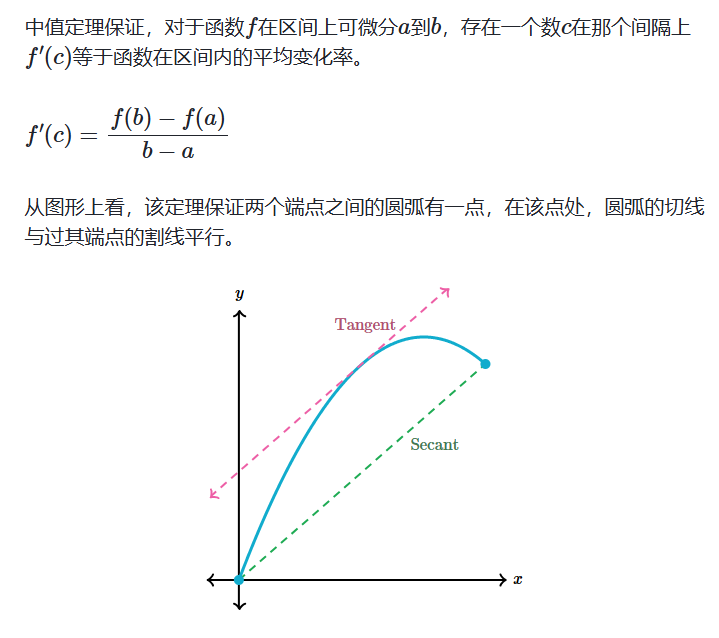
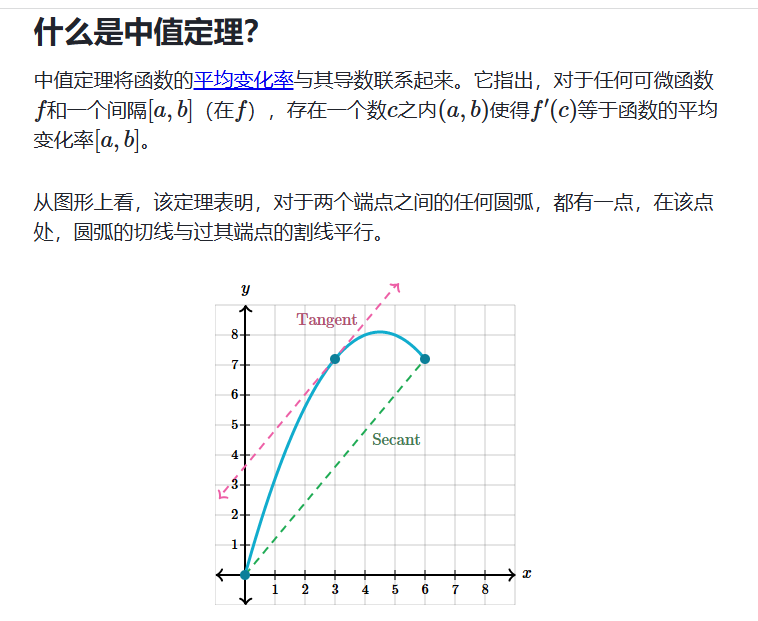
中值定理

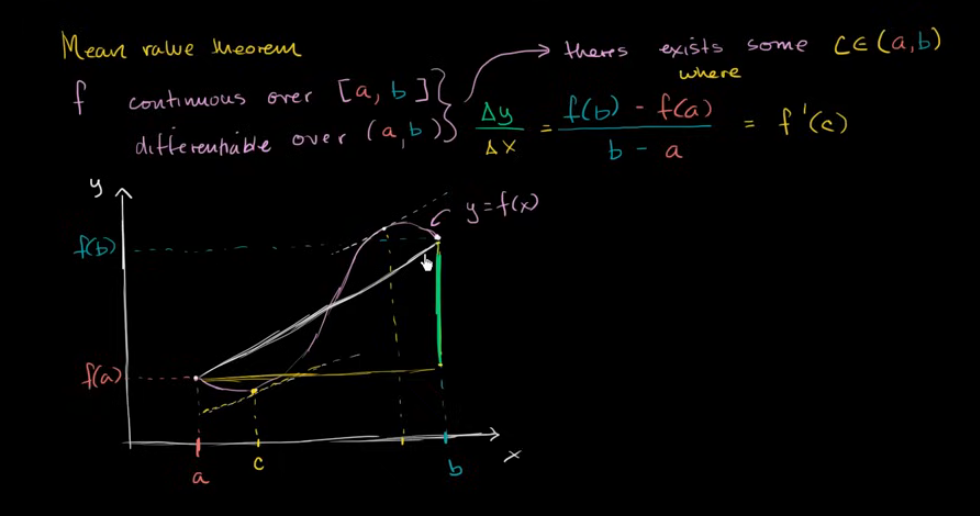
1. 闭区间要连续的

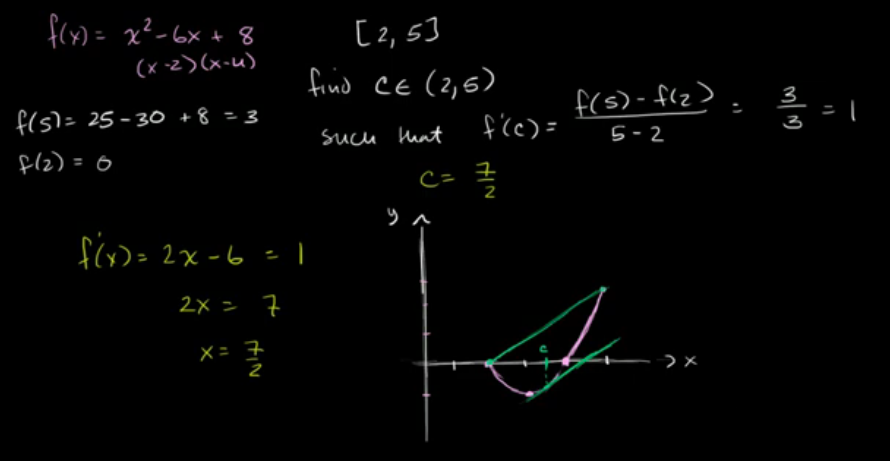
均值定理示例：多项式

c在7/2的时候是有一条线跟他的斜率是一样的

 

均值定理示例：平方根函数

 2/根号4c-3 ,把1.75代入是等1的

用中值定理证明：表格

 

用中值定理证明：方程

 

建立 MVT 的可区分性

 

 

 

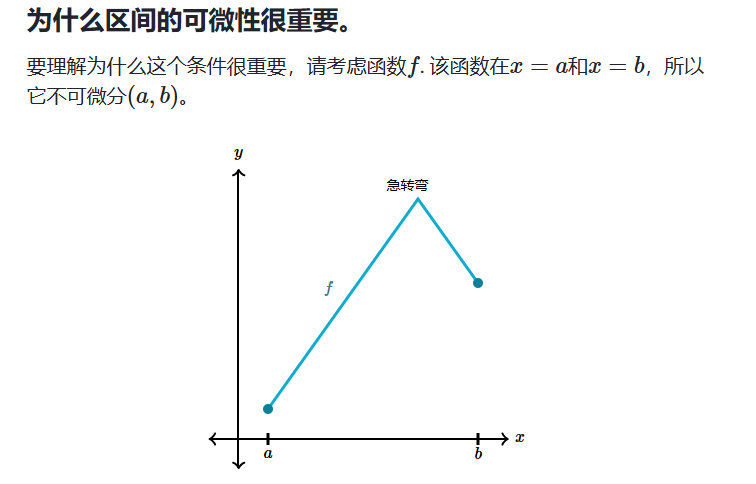
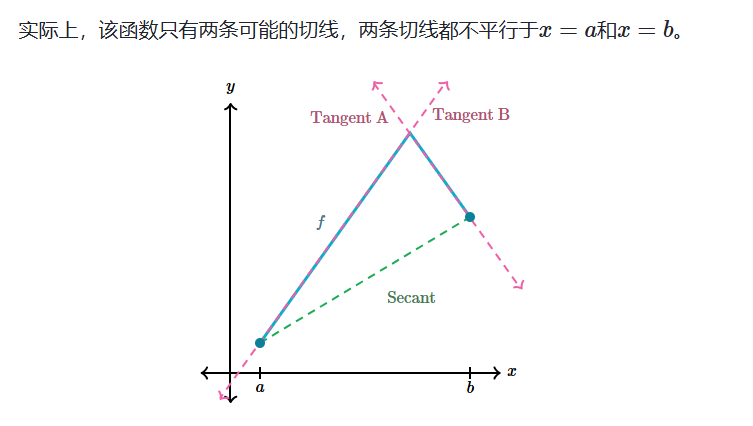
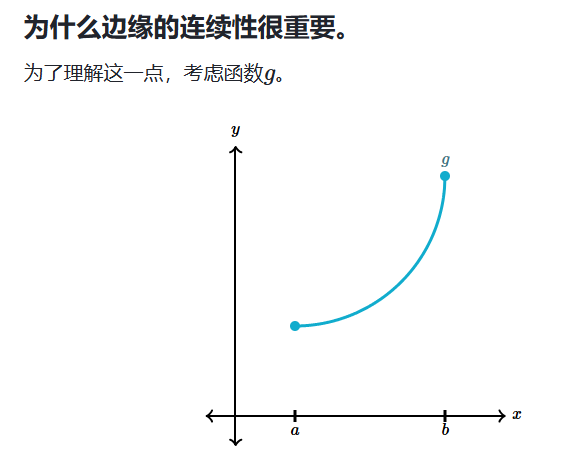
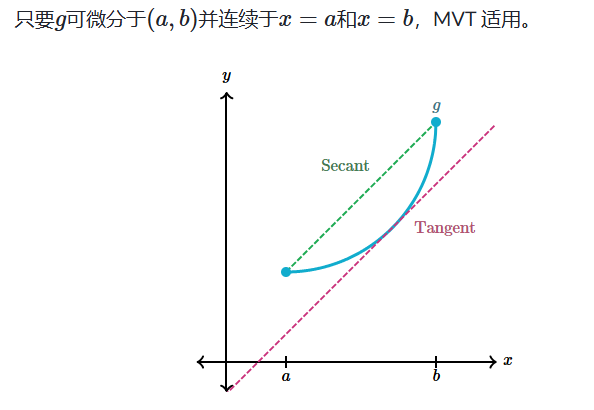
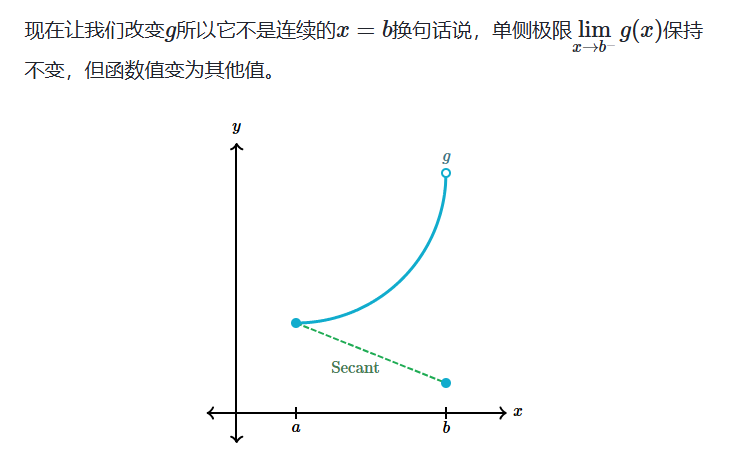
极值定理

如果在闭区间【a,b】是连续的，一定存在一个最大值和一个最小值

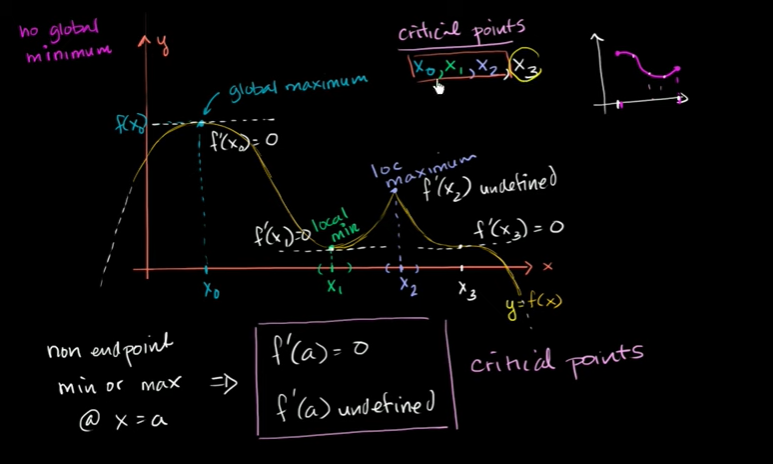
关键点介绍

局部最小值，局部最大值

临界点，不存在导数

 

寻找关键点

因为临界点不存在导数，所以导数是0的，只要导数是0，那么反过来求到零界点

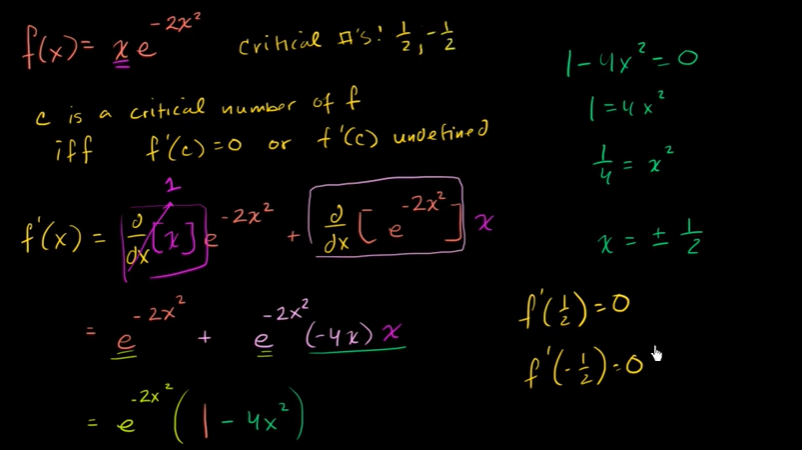
 例子：

 

 

给定函数寻找递减区间

 

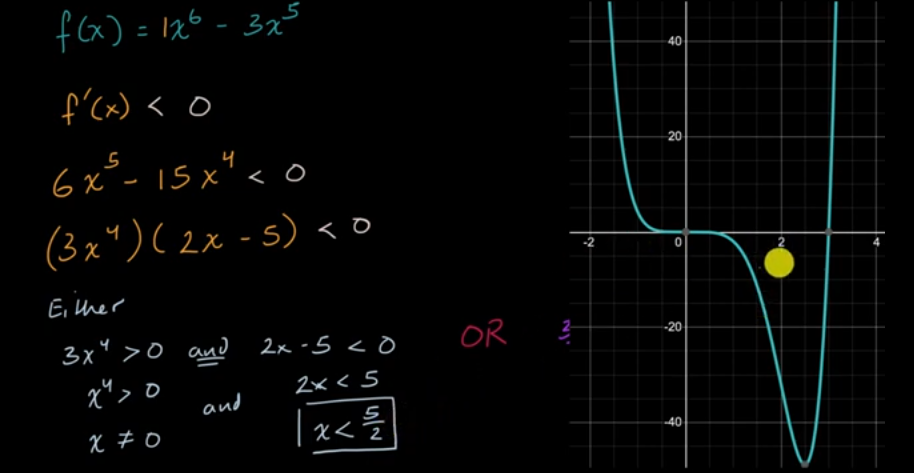
给定导数寻找增加区间

 例子：

 例子：

 

 

 

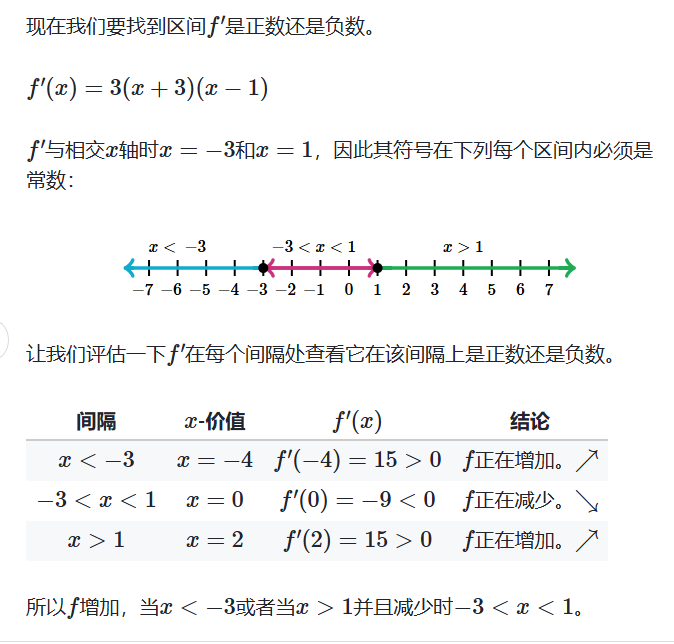
最小点和最大点简介

 

 

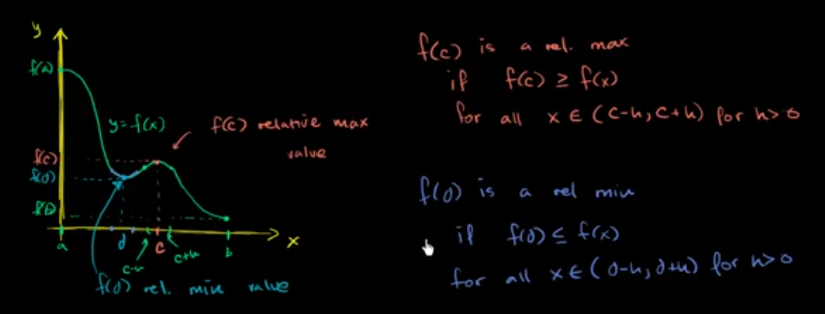
寻找相对极值（一阶导数检验）

左边上右边下才符合，x3不符合

 

示例：寻找相对极值

 

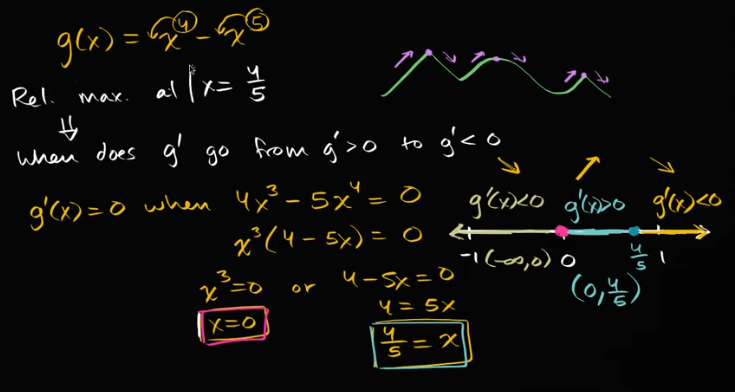
例子：

 

 

 

 

在闭区间内寻找绝对极值

 例子： e和ln

 

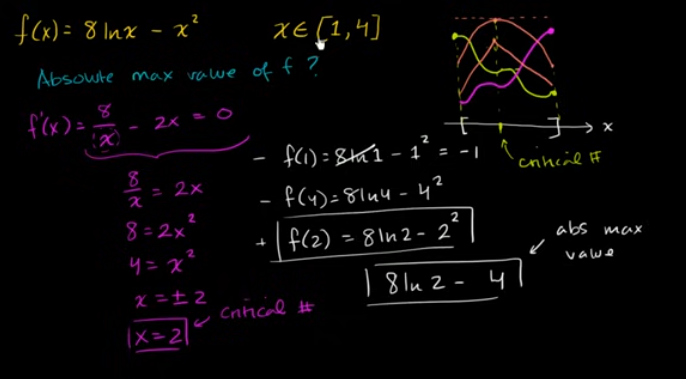
 例子：

 

 

例子：

 

绝对最小值和最大值（整个域）

 

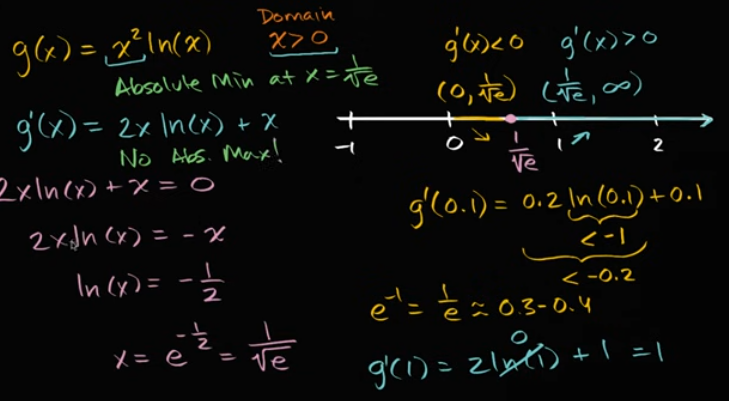
 练习：

 

 

 所以C也是成立的

 

 

 

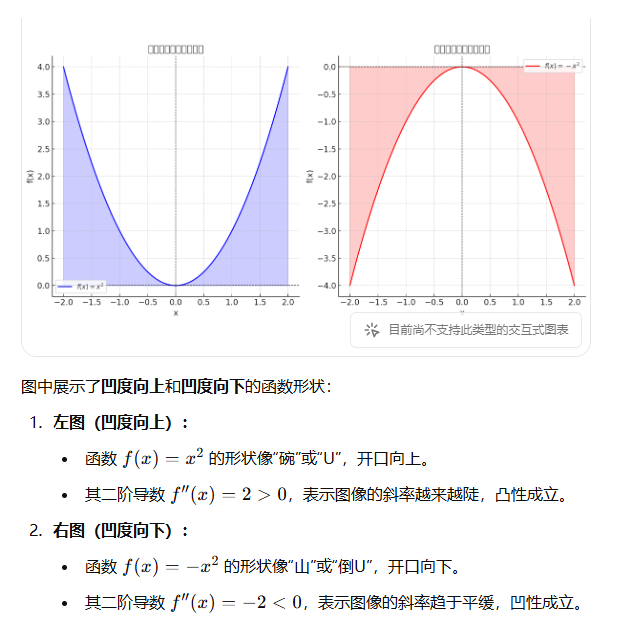
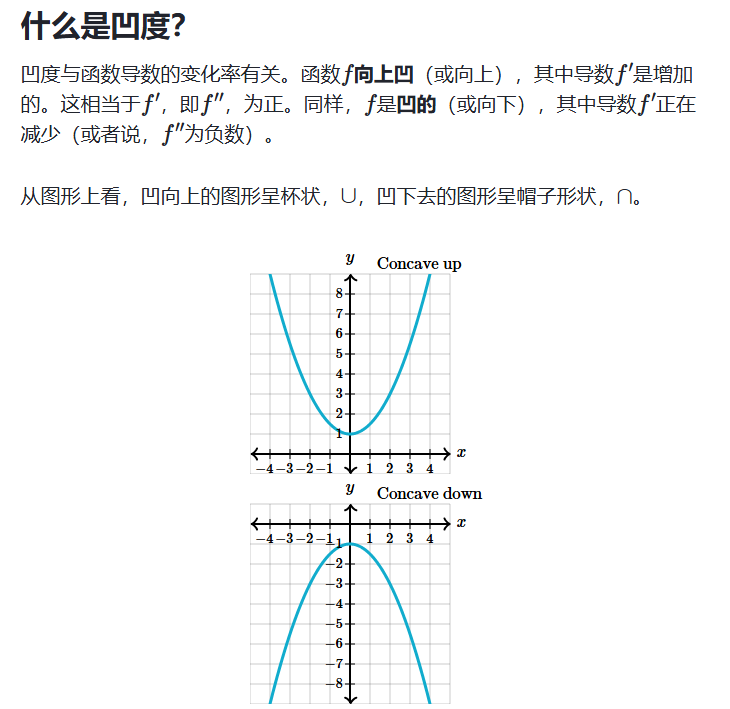
凹度介绍

例子：

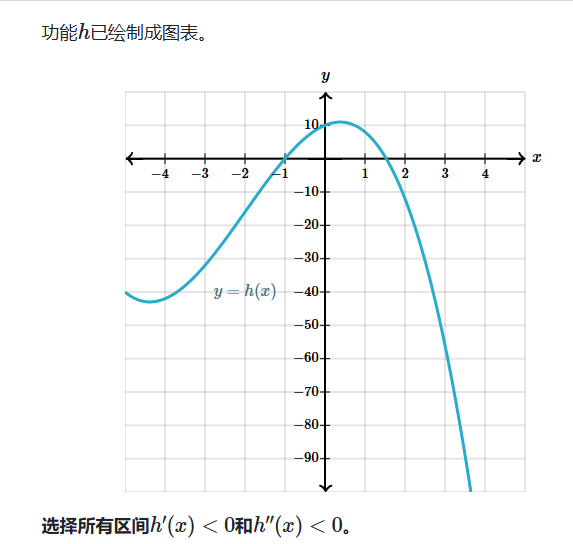
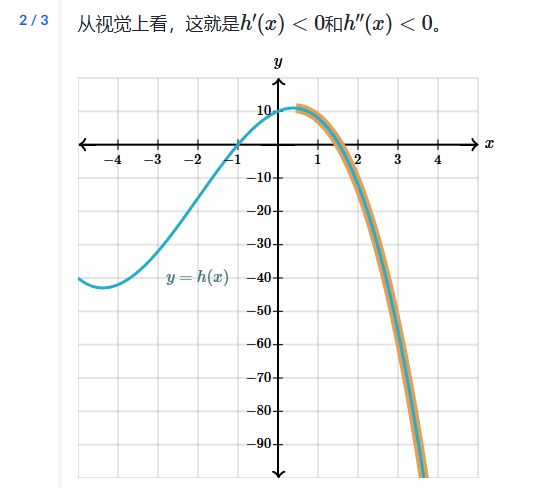
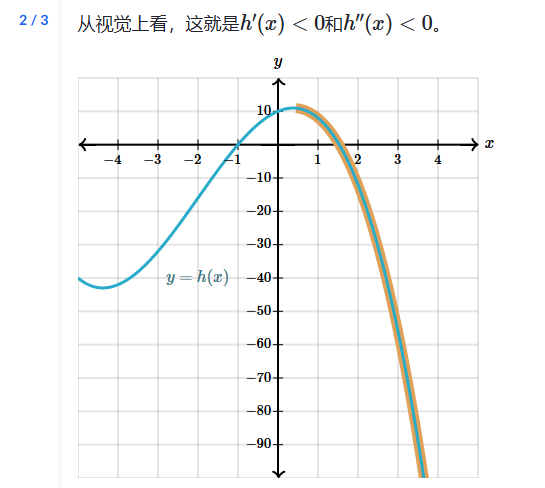
 例子：

 

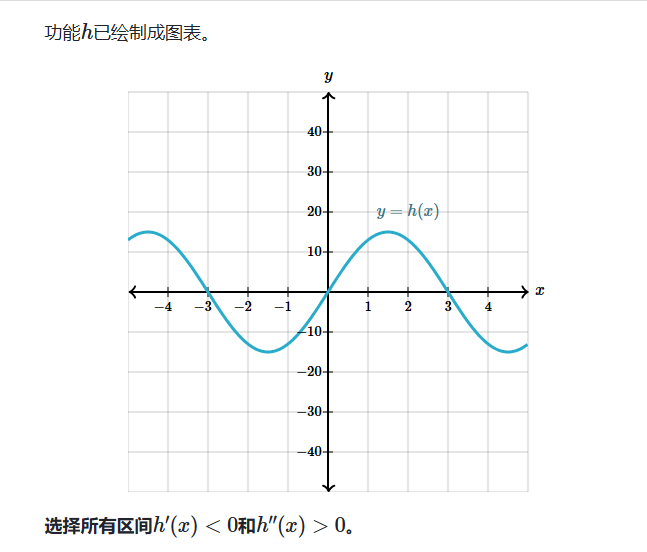
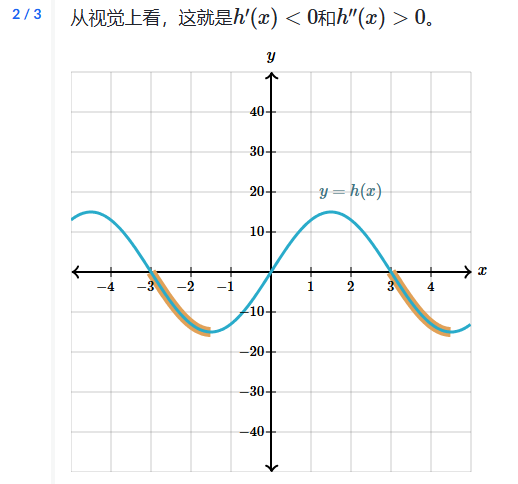
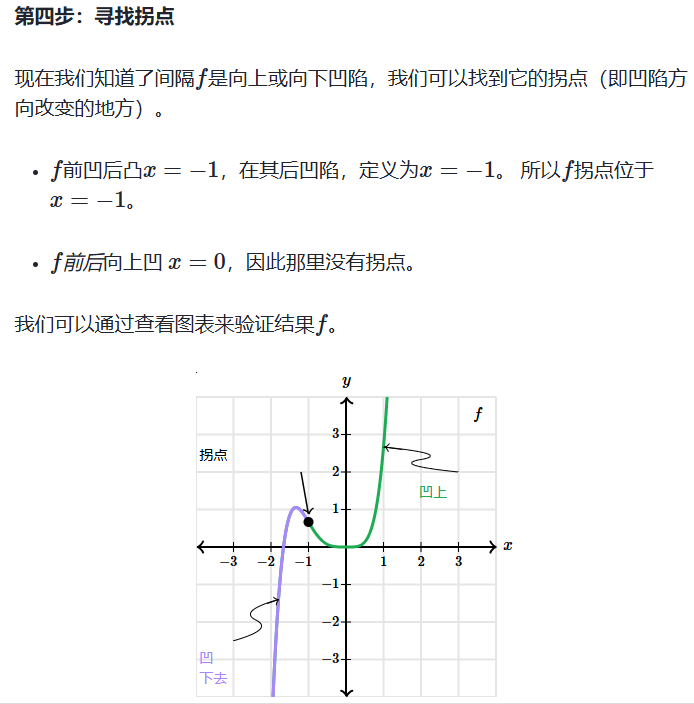
拐点介绍

二阶导数会变符号，正变成负，负变正

 

 

拐点（图形）

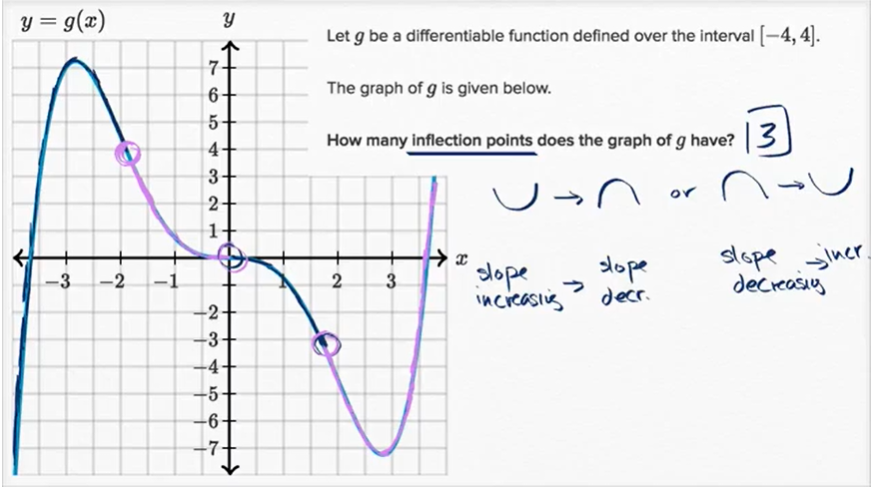
 例子：

 

 

 

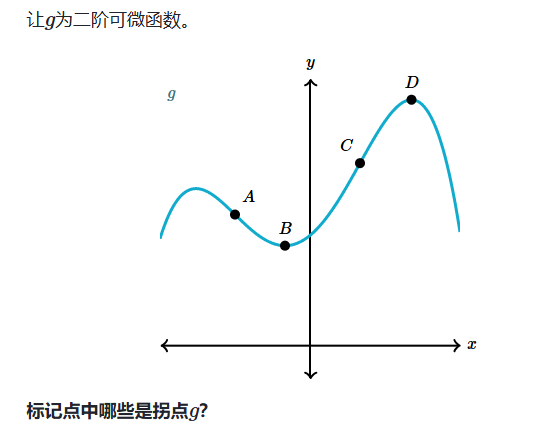
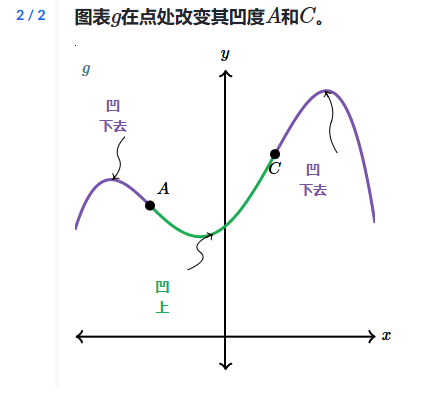
分析凹度（代数）

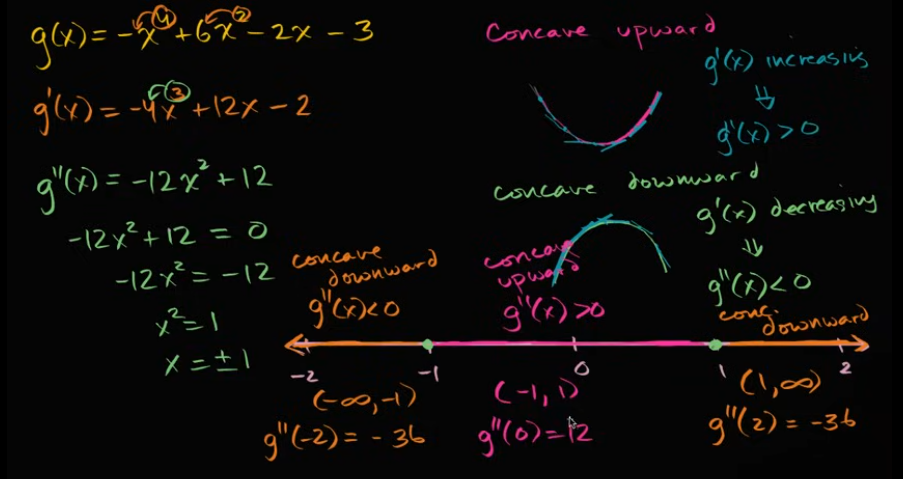
 例子：二次求导之后，看是上还是下

 

 

拐点（代数）

没有拐点

 

 

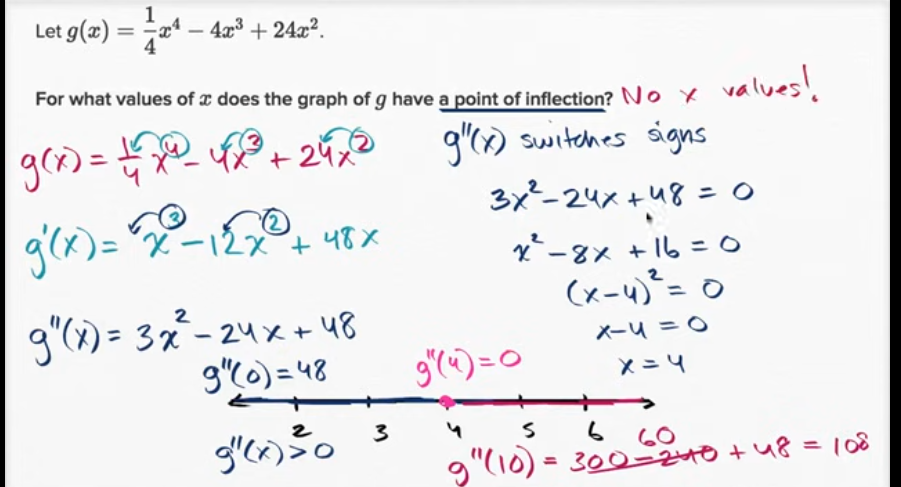
分析二阶导数寻找拐点

 

 

 

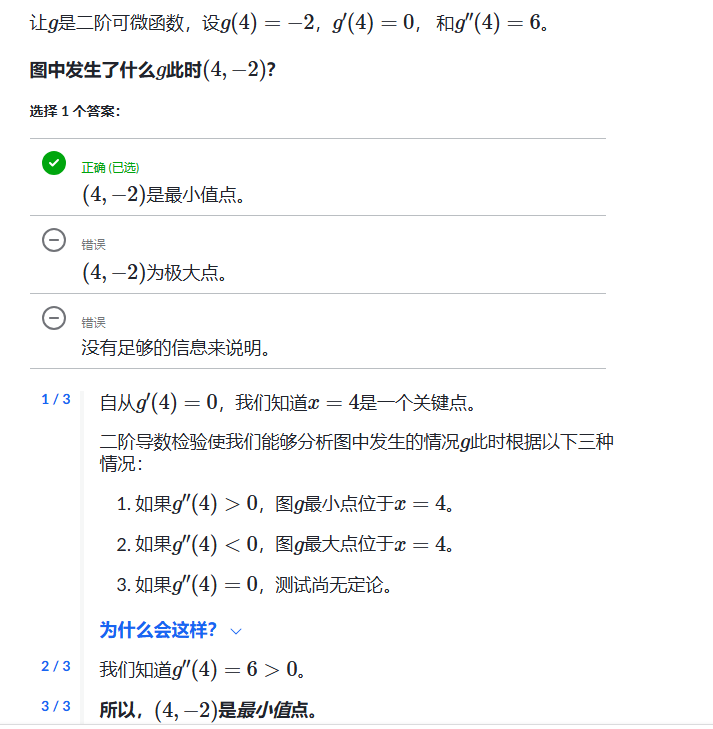
二阶导数检验

 例子：

 

 例子：

 

 

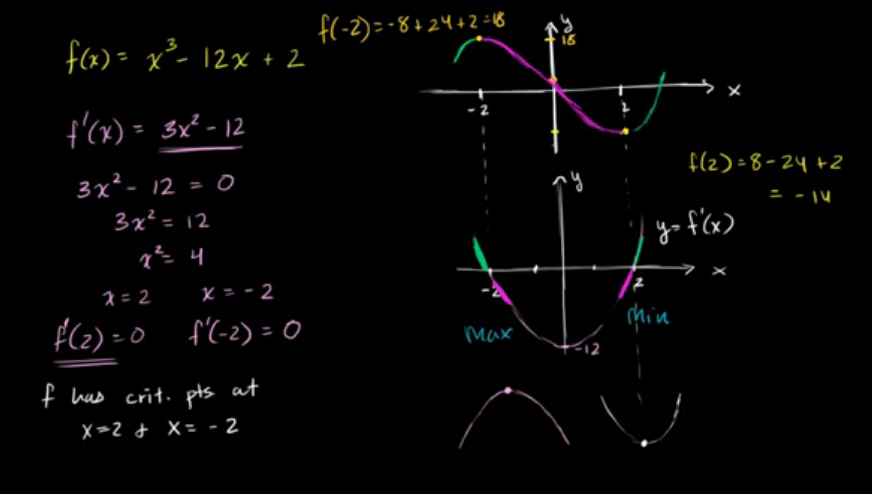
用微积分绘制曲线：多项式

 

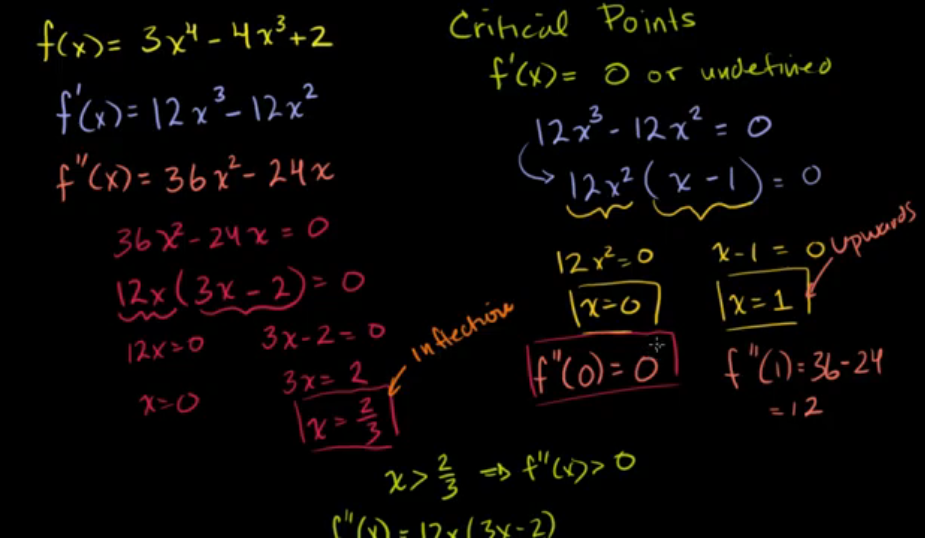
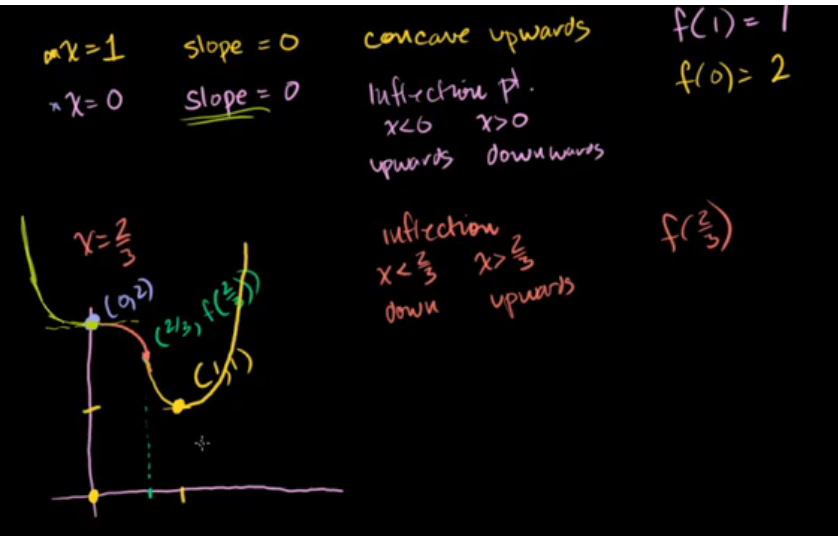
用微积分绘制曲线：对数

 

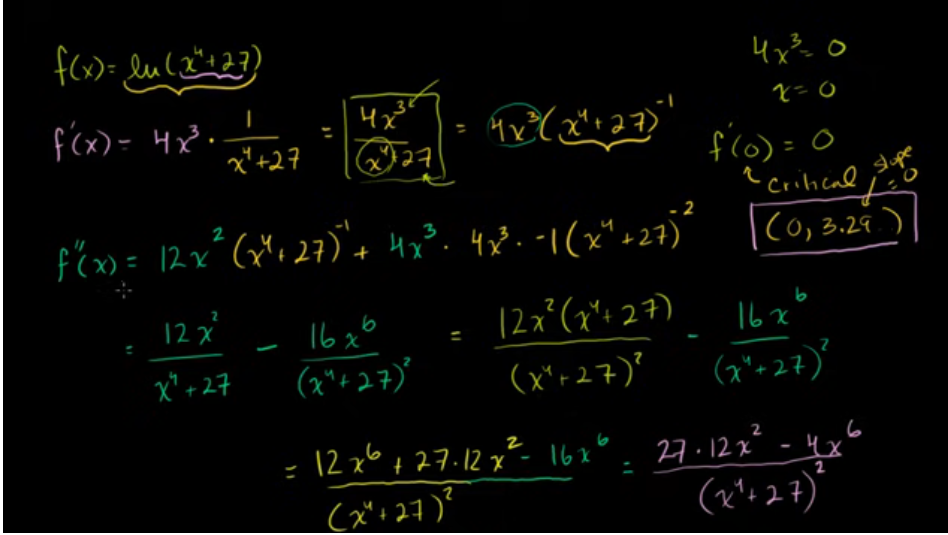
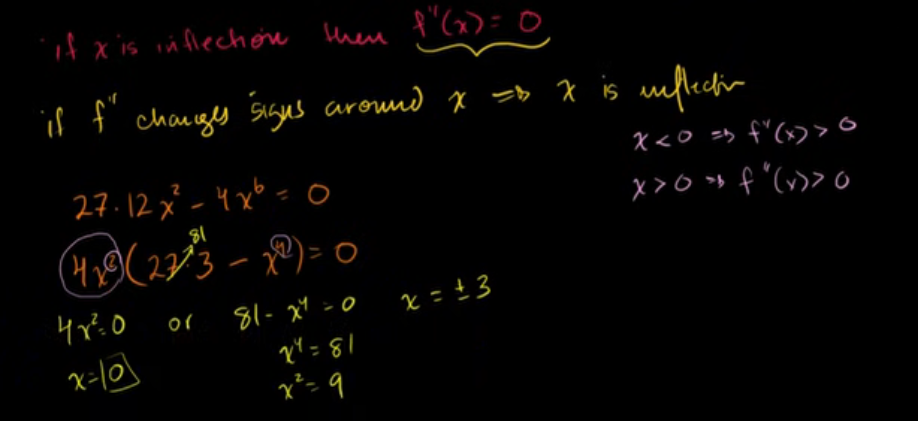
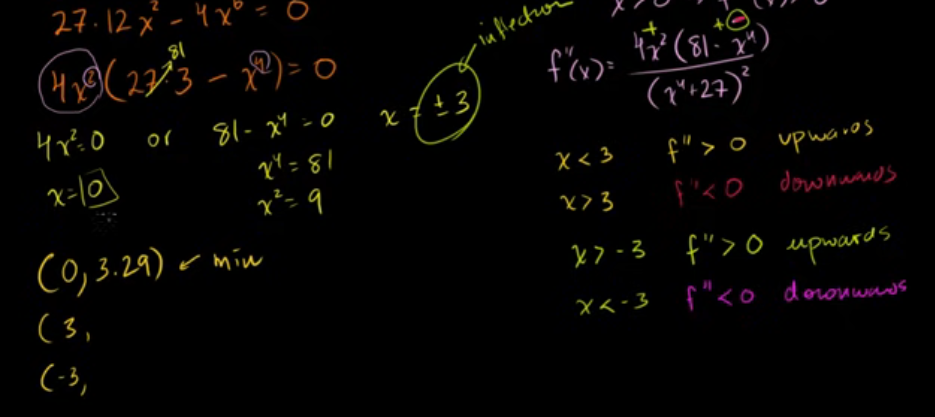
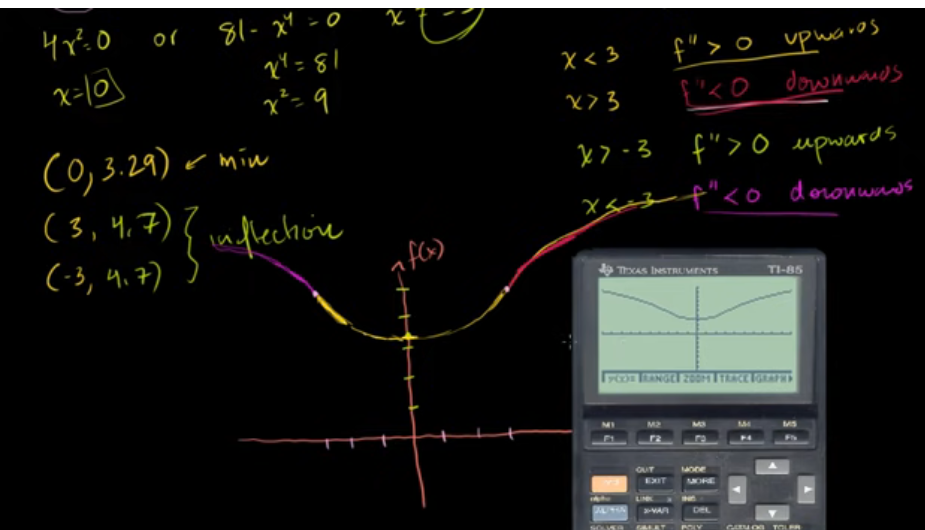
用导数分析函数