第 3 单元:微分:复合函数、隐函数和反函数 (链式法则、复合函数、aˣ 的导数、ln(√x) 的导数、cos³(x) 的导数、logₐx 的导数)(隐式微分、反函数的导数、反正弦的导数)(二阶导数)
链式法则
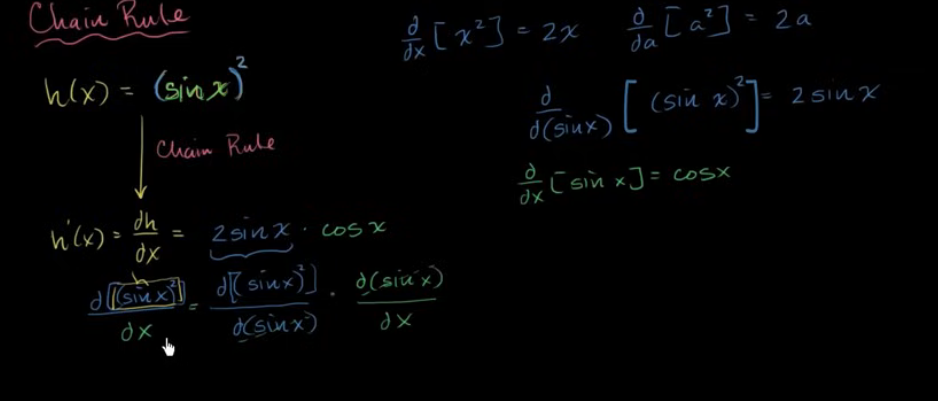
常见的链式法则误解



例子:


例子:



识别复合函数
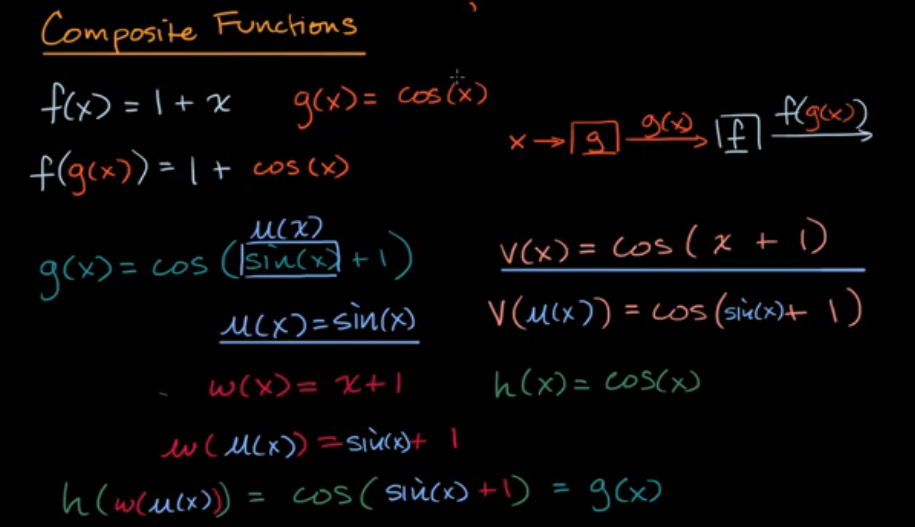
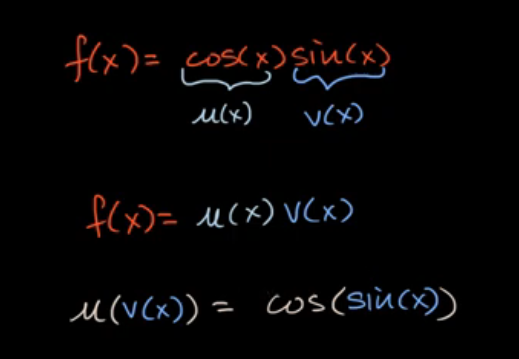
例子:

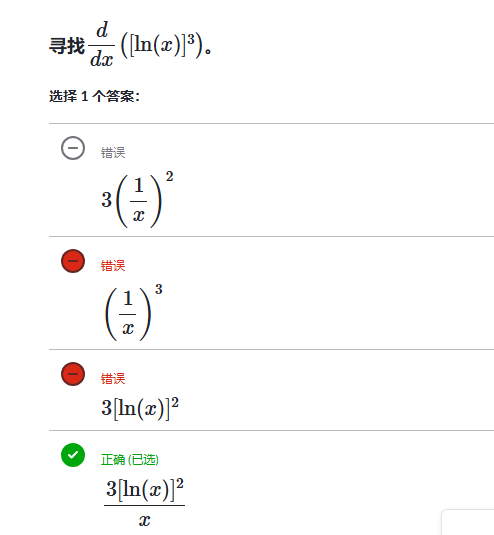
例子:利用链式法则求 cos³(x) 的导数
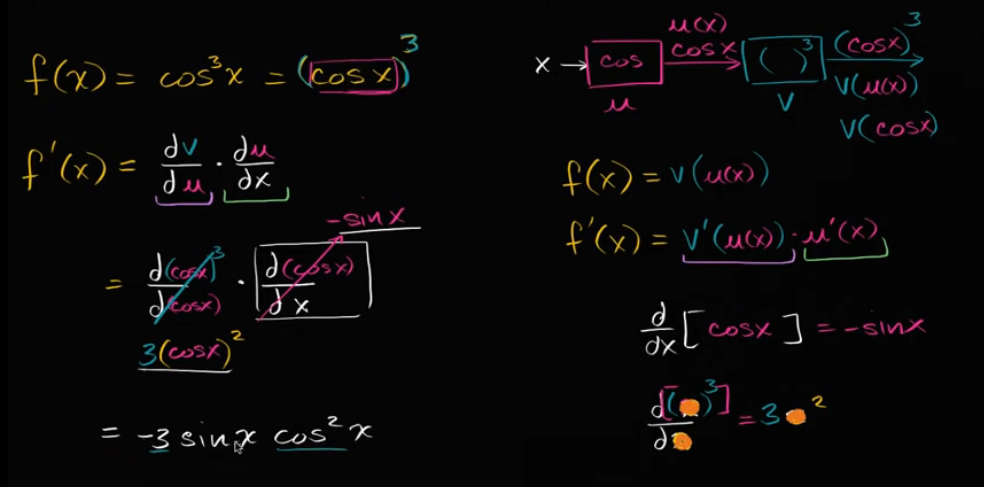
例子:利用链式法则求 √(3x²-x) 的导数
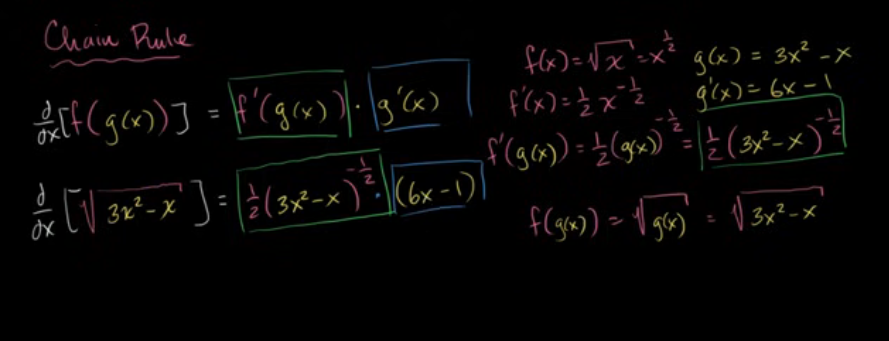
例子:利用链式法则求 ln(√x) 的导数
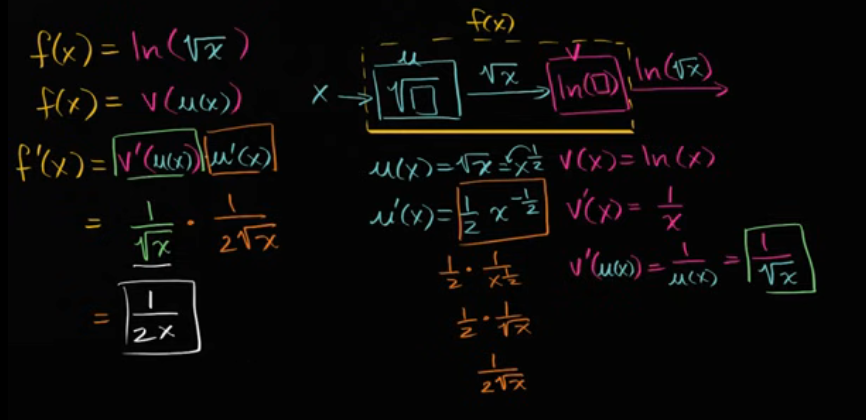
例子:


示例:带表格的链式法则

aˣ 的导数(对于任何正基数 a)



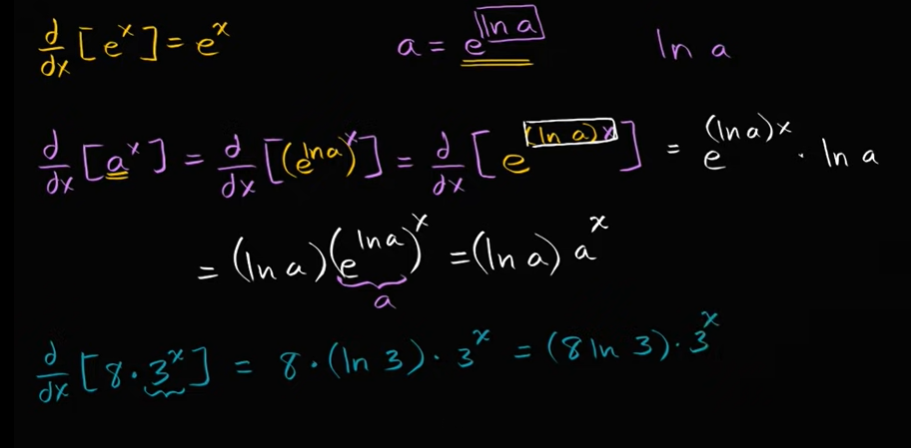

例子:


logₐx 的导数(对于任何正底 a≠1)
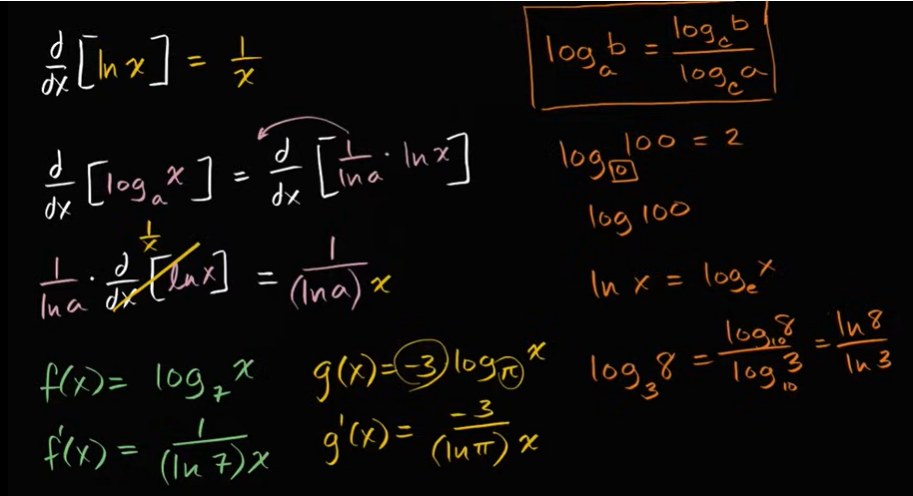

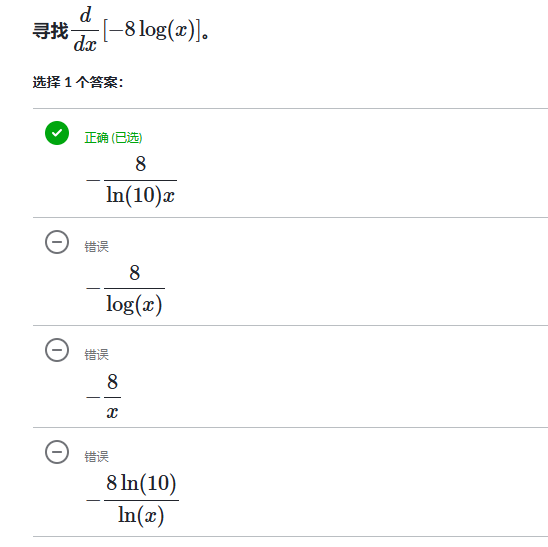
例子:
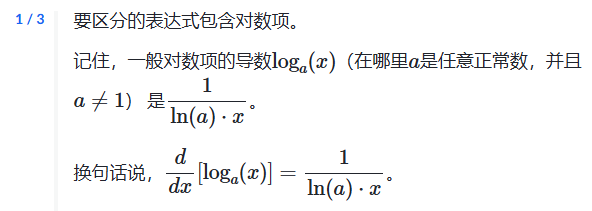


示例:利用链式法则求 7^(x²-x) 的导数
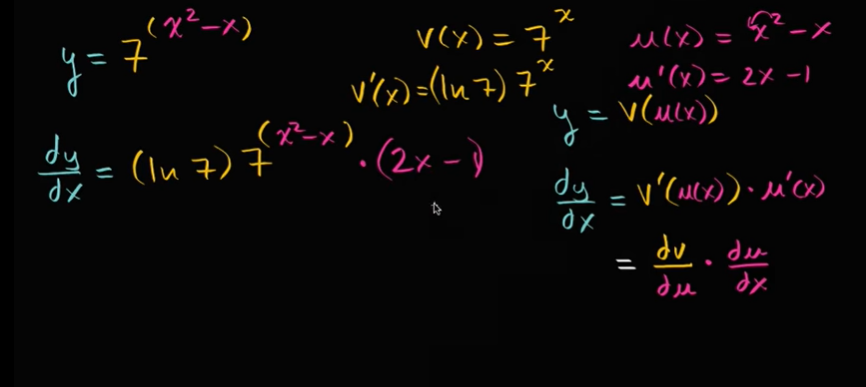
例子:利用链式法则求 log₄(x²+x) 的导数
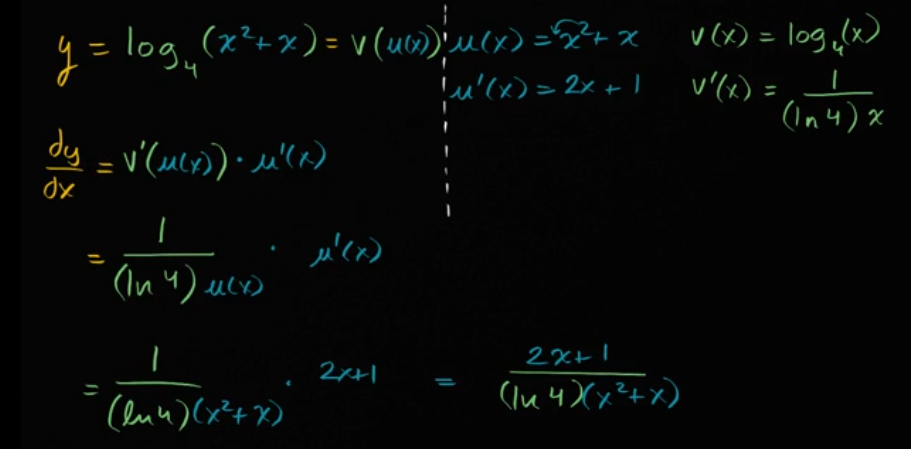

例子:利用链式法则求 sec(3π/2-x) 的导数

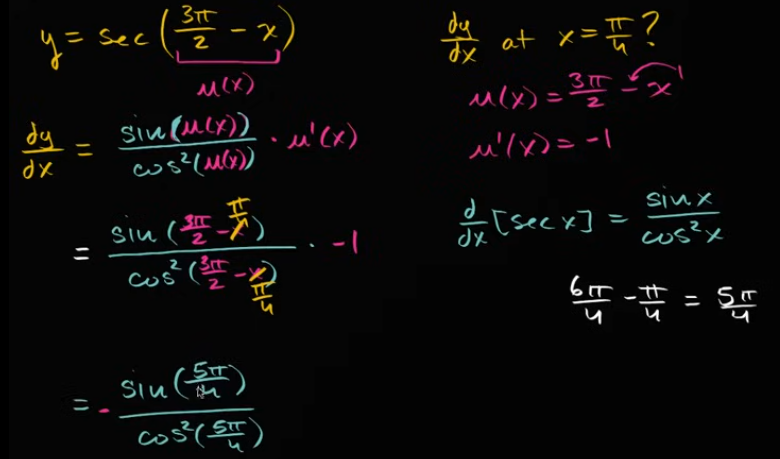


例子:利用链式法则求 ∜(x³+4x²+7) 的导数
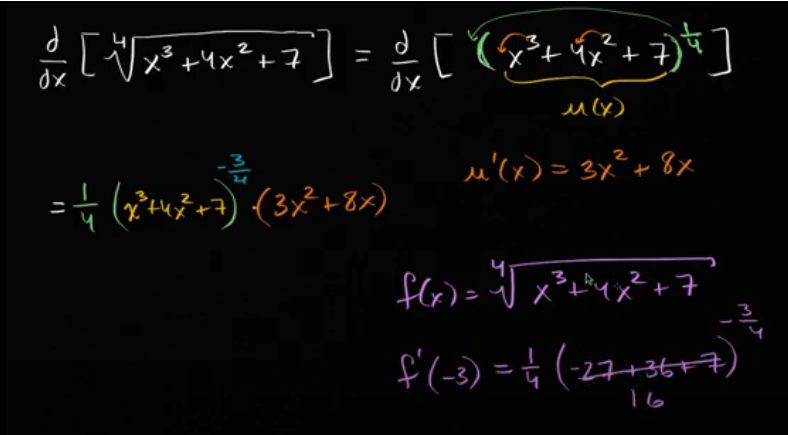
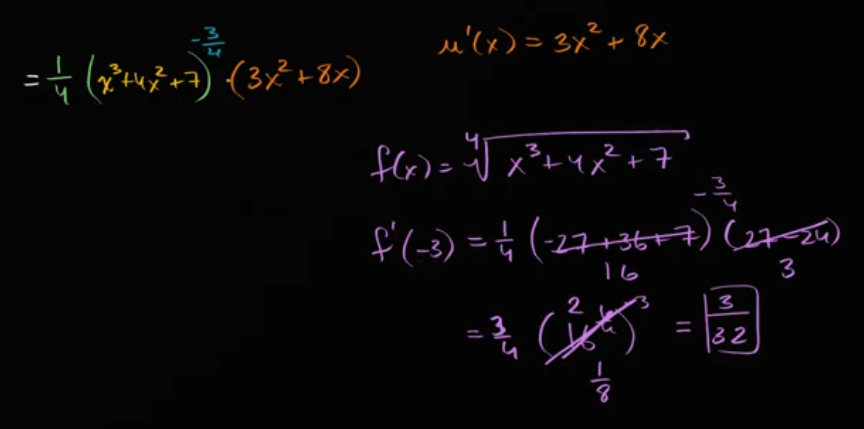
链式法则顶峰
例子:

证明链式法则


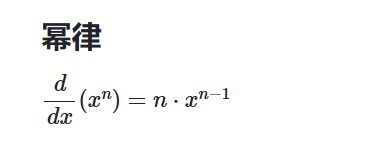
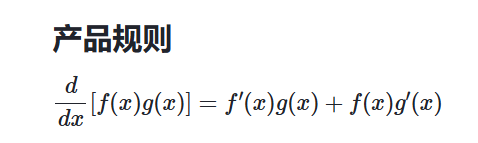
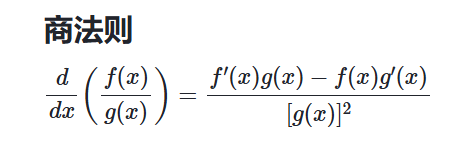
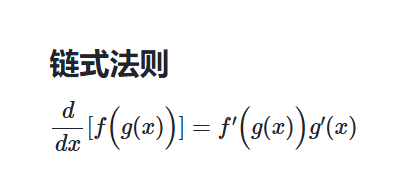
隐式微分
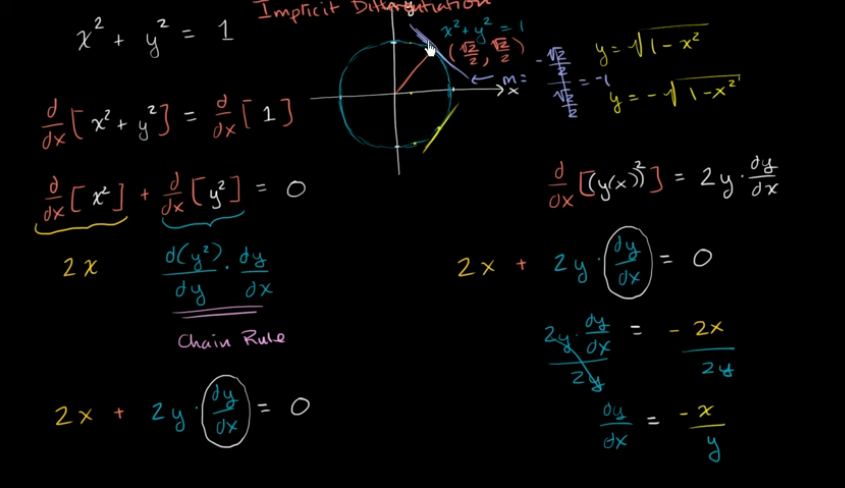
示例:隐式微分
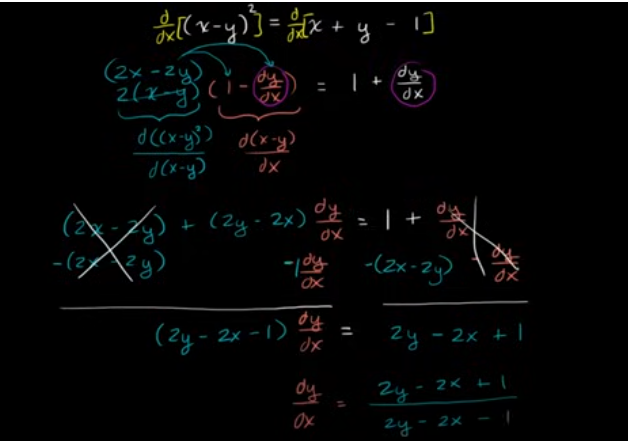
示例:利用隐式微分求导数
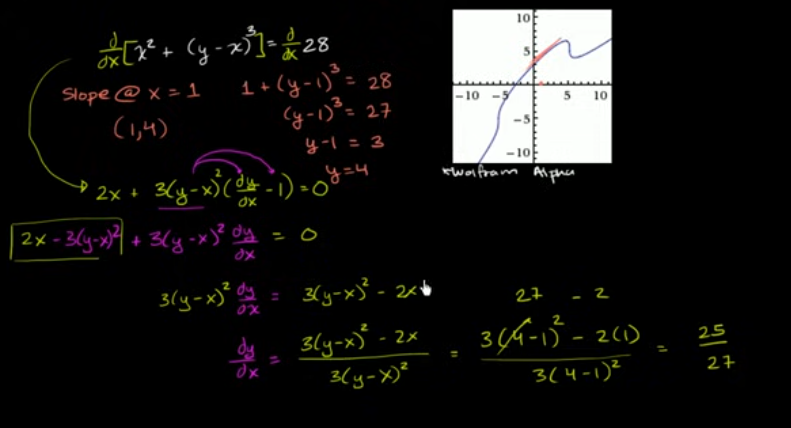
例子:



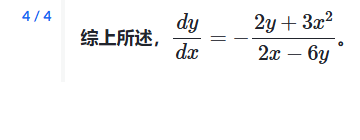
例子:



显示显式和隐式微分给出相同的结果
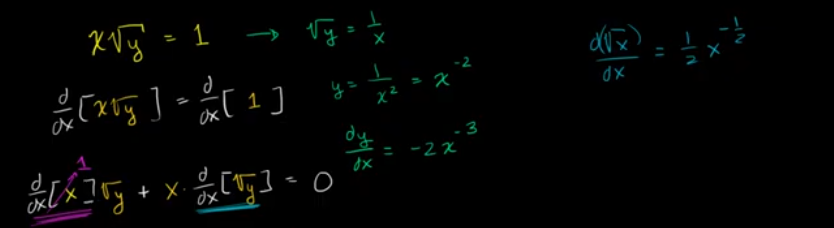
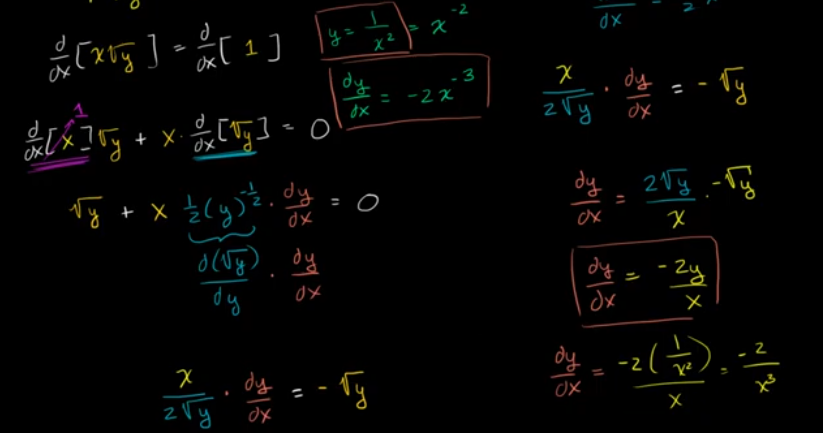



反函数的导数

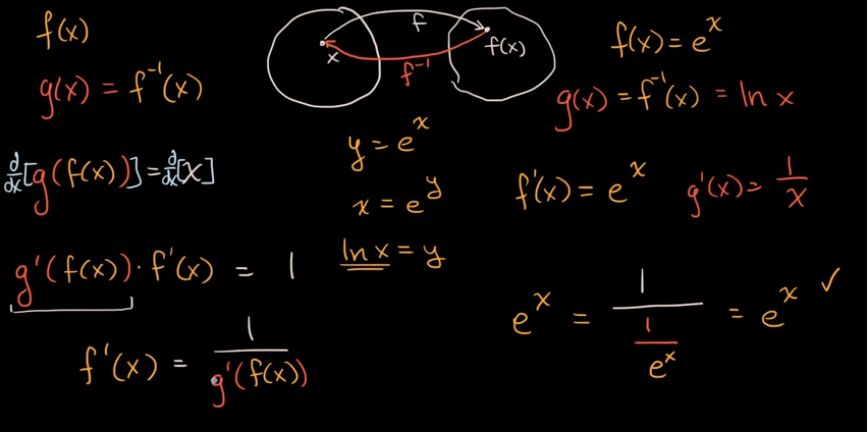
反函数的导数:根据方程
两边除h(x)

反函数的导数:来自表格

例子:



例子:




反正弦的导数
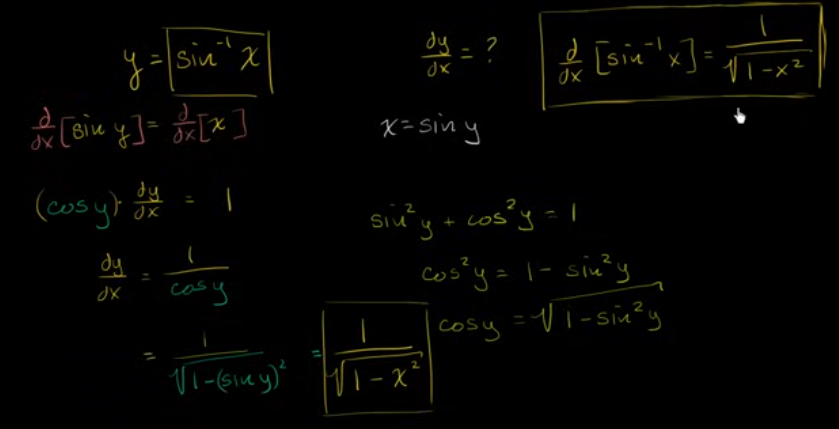


反余弦的导数
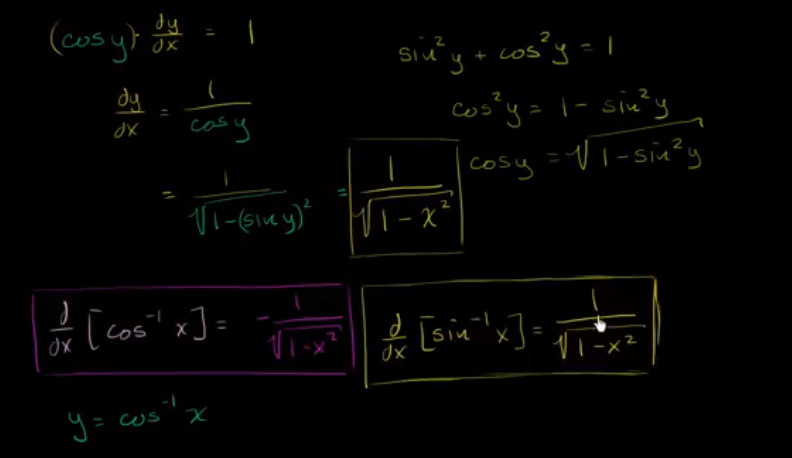
反正切的导数
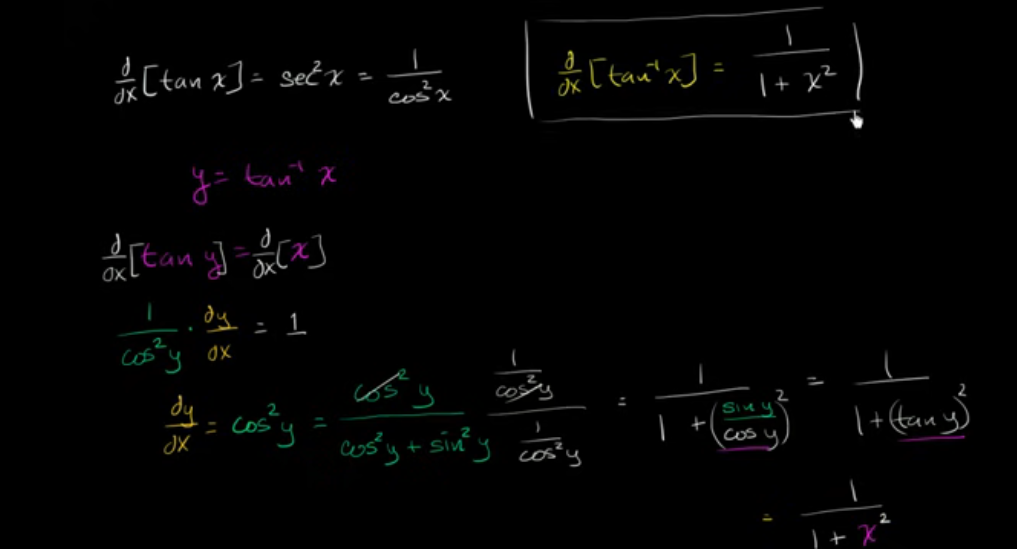

区分函数:查找错误

在微分之前操作函数(使用之前可以先简化,例如除的使用乘的公式)
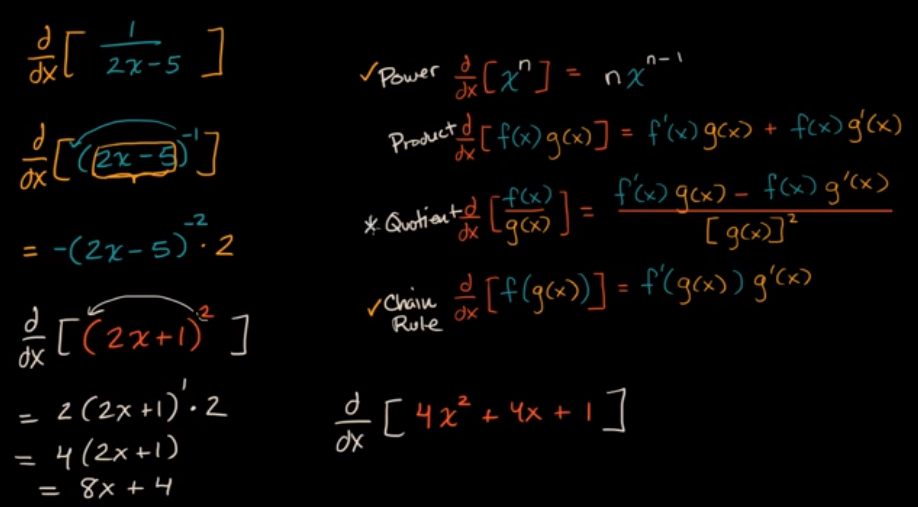


使用多种规则进行区分:策略
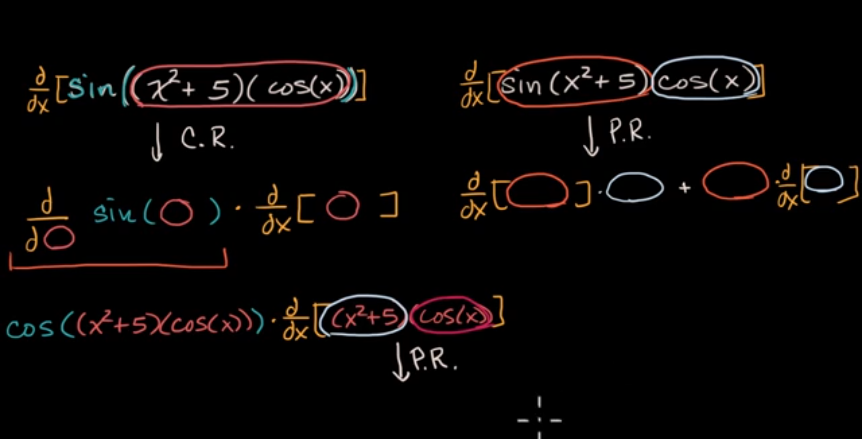
应用链式法则和乘积法则
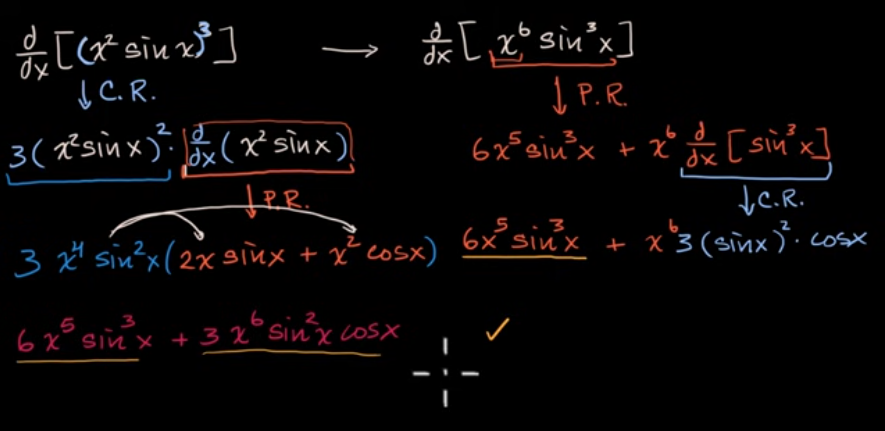
应用链式法则两次
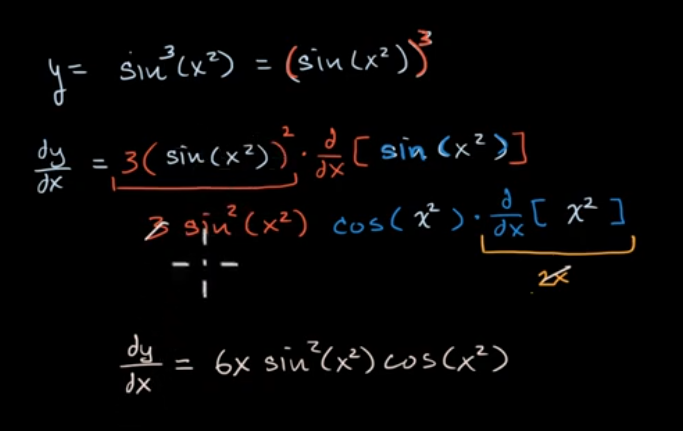
eᶜᵒˢˣ⋅cos(eˣ) 的导数
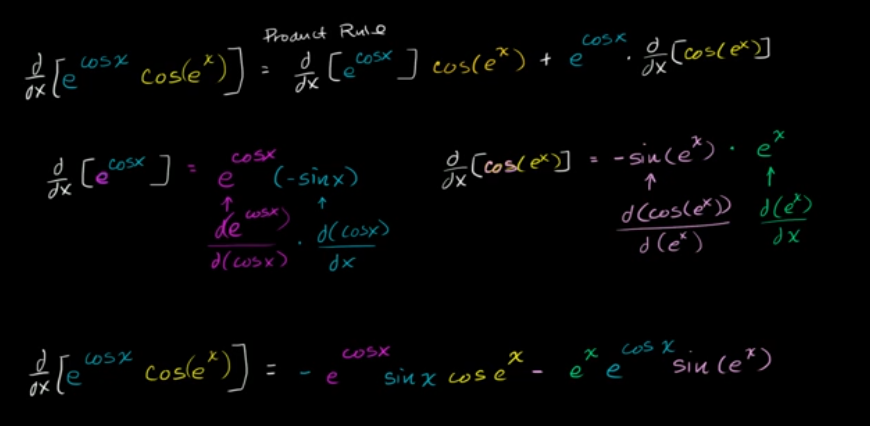
sin(ln(x²)) 的导数
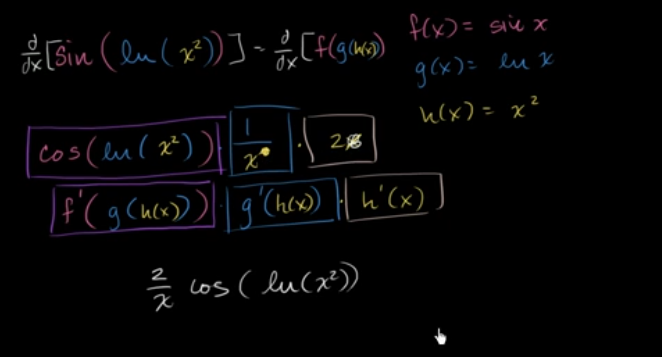
二阶导数
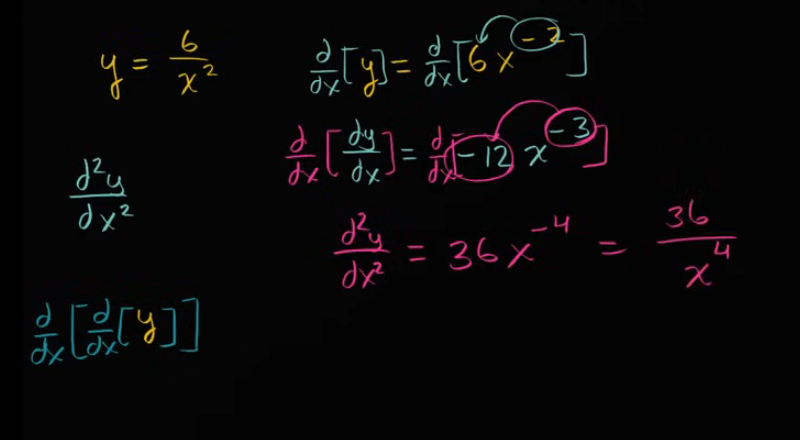

例子:



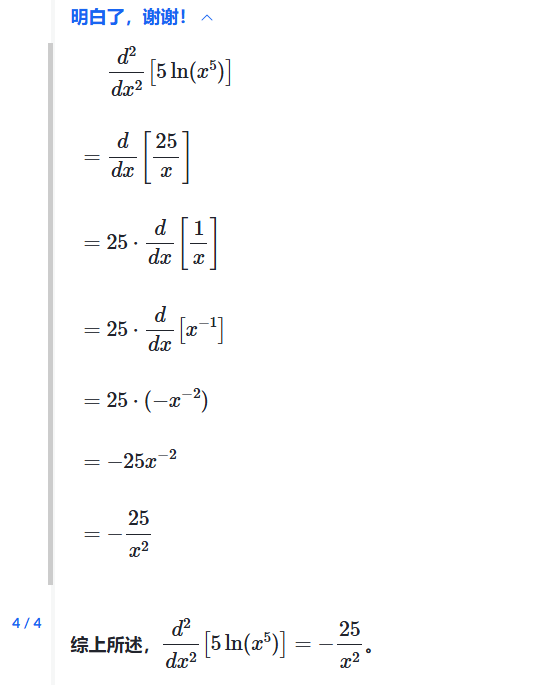
二阶导数(隐式方程):求表达式
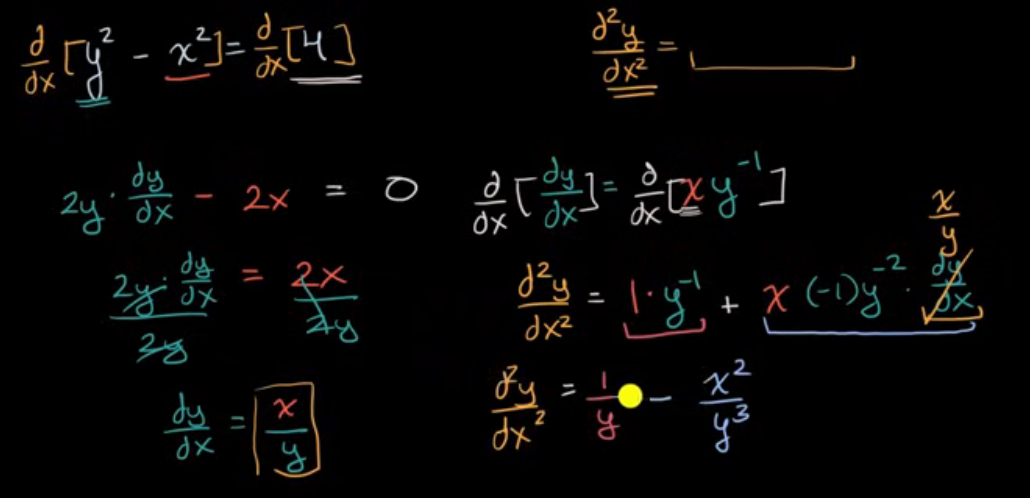
二阶导数(隐式方程):求导数

例子:



例子:注意y其实是1,就是dy/dx



例子:注意负号的符号要放最左边,其实就是-1

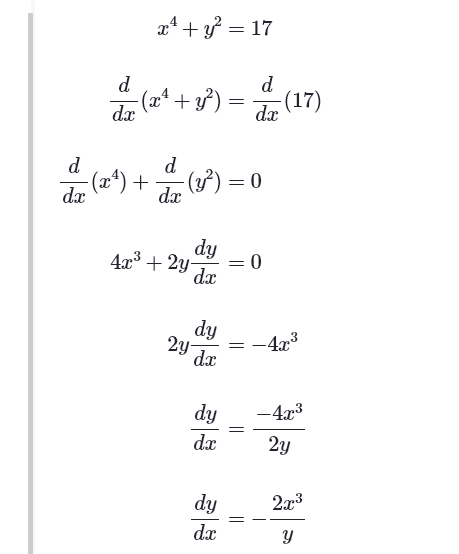
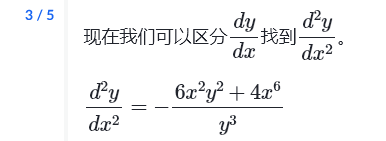


隐蔽衍生品

例题:
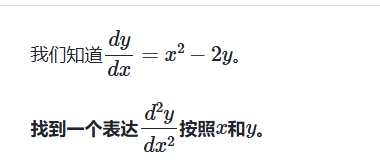





 浙公网安备 33010602011771号
浙公网安备 33010602011771号