大学微积分 AB （第二单元）微分：定义和基本导数规则 （导数和切线方程、可微分和连续、基本导数规则,sin(x) 和 cos(x) 的导数、ln(x) 的导数、𝑒ˣ 的导数）

 

直线方程

 

 

 

 

 

 

 

1. 牛顿、莱布尼茨和尤塞恩·博尔特

瞬间的速率。dy/dx  代表很小很小的变化量

 

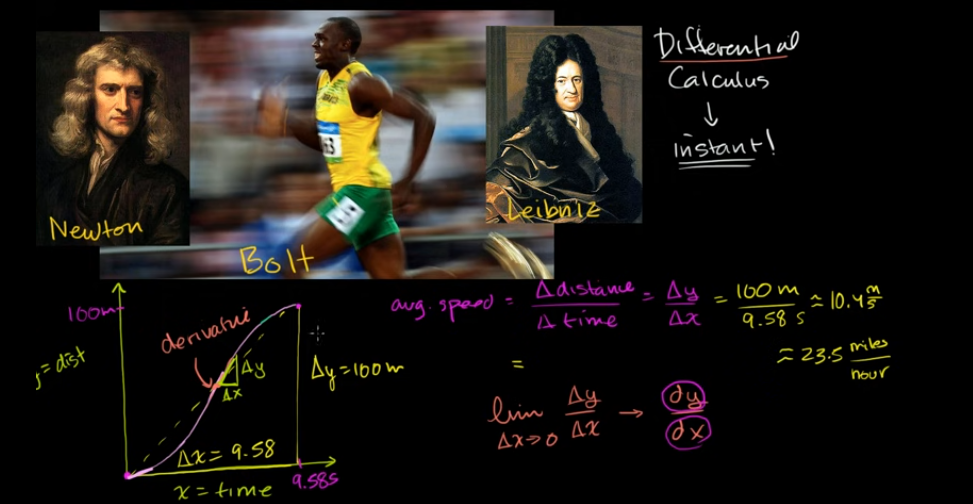
衍生品的概念

符号表示方式

 

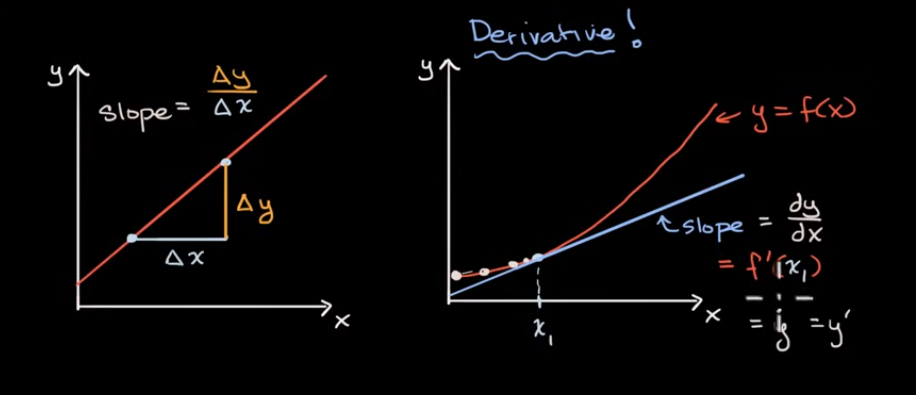
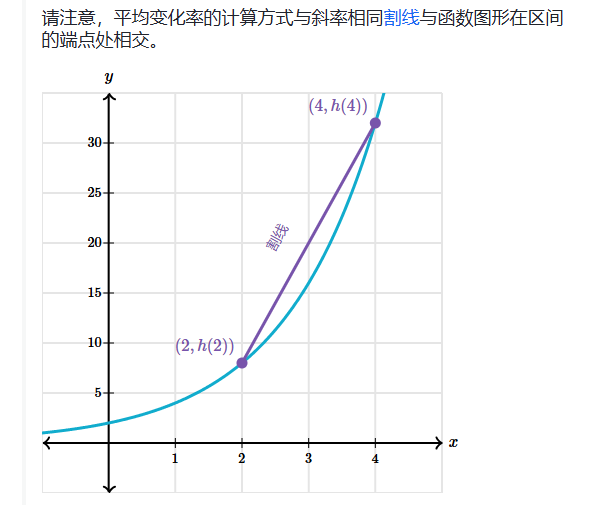
割线和平均变化率

 

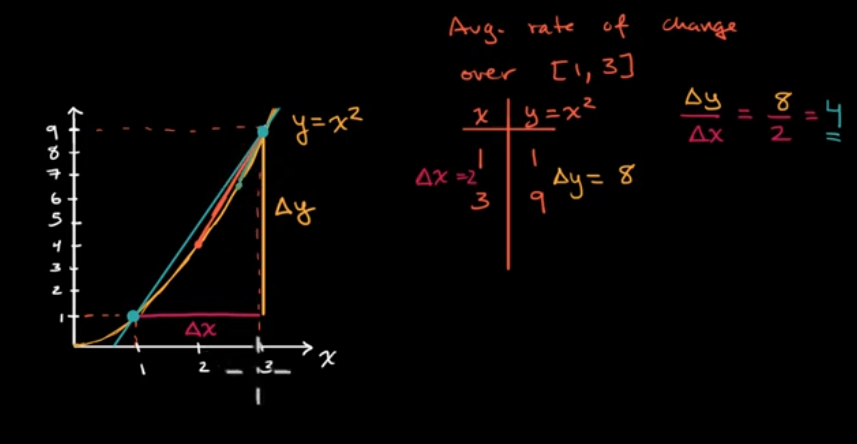
导数符号复习

 

 

导数作为曲线的斜率

 

 

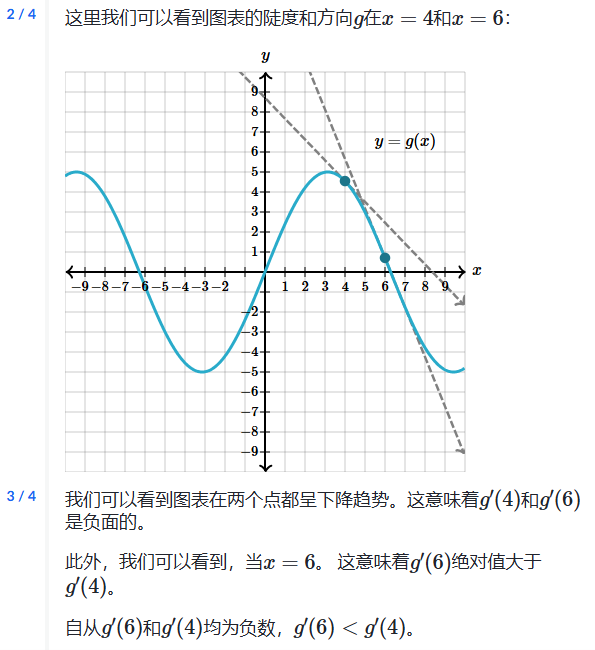
2.导数和切线方程

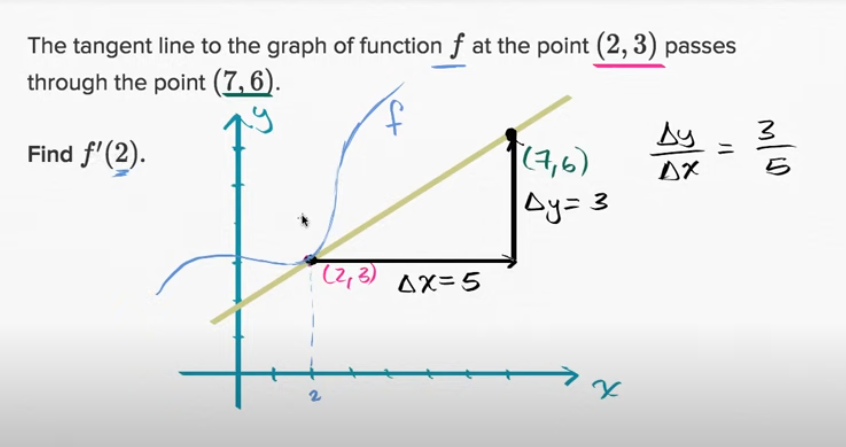
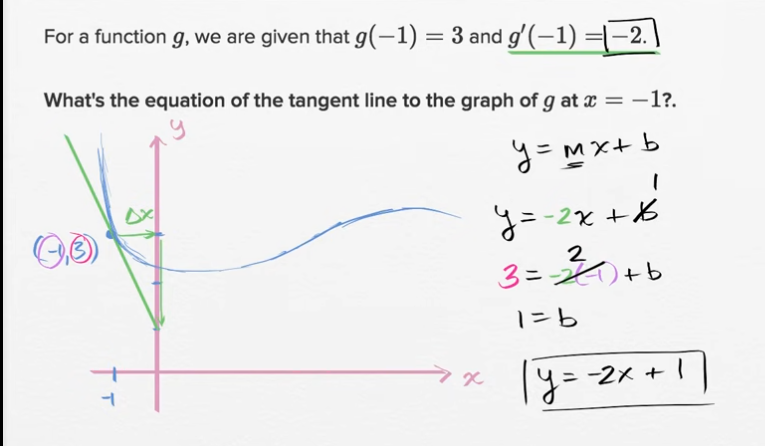
 例子：

 

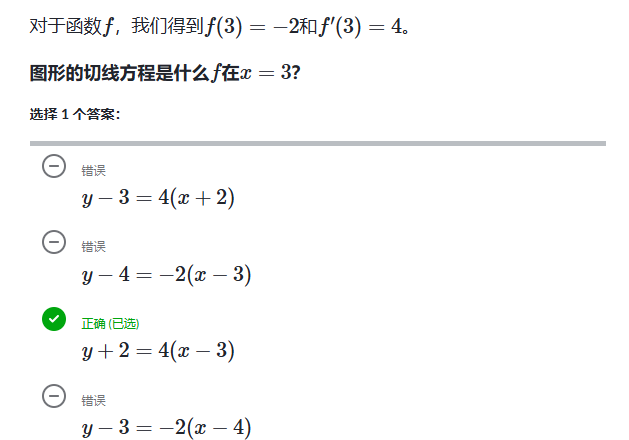
例子：

 

 

 

 

导数的正式定义是极限

 

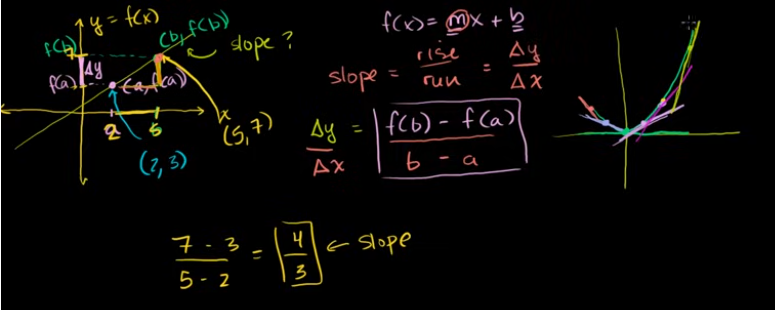
衍生品的正式形式和替代形式

 

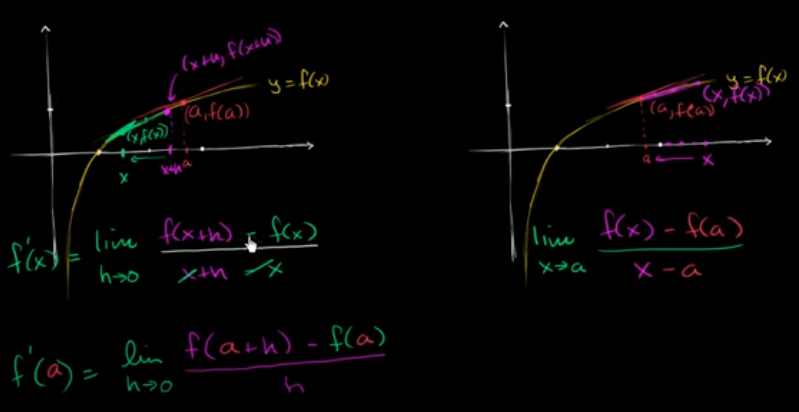
例子：导数作为极限

 

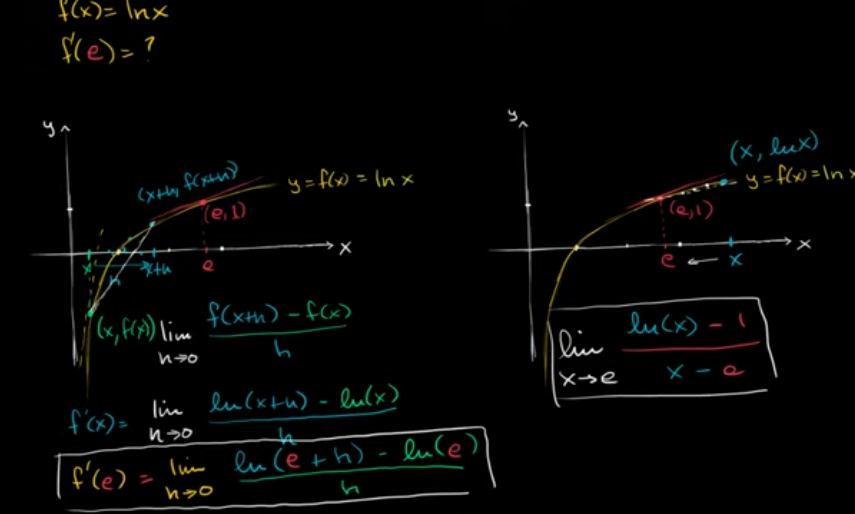
例子：从极限表达式求导

 

 

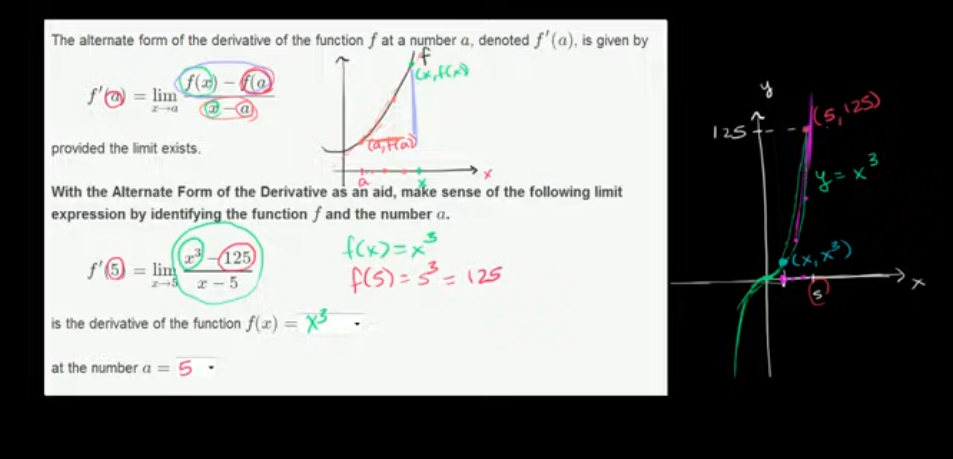
使用正式定义，求 x² 在 x=3 处的导数

 

 

使用正式定义求任意一点 x² 的导数

 

 

 

 

 

 

 

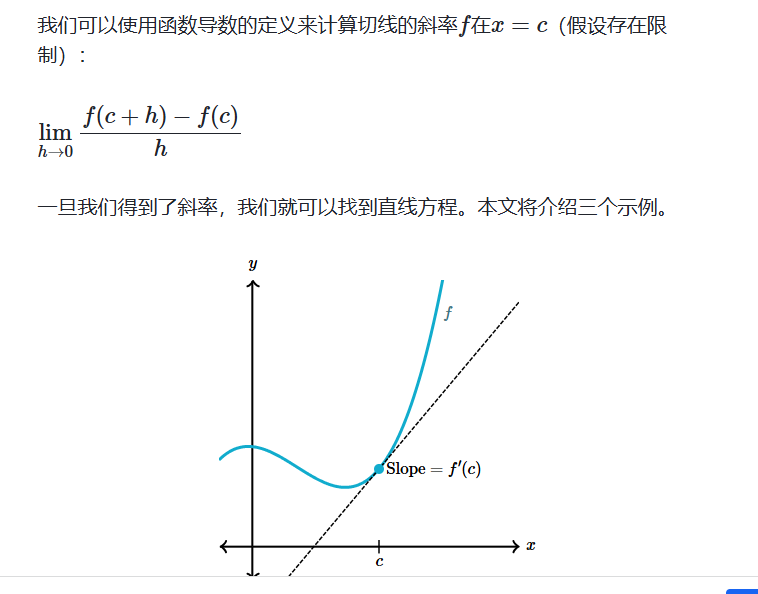
估算衍生品

 

 

 

 

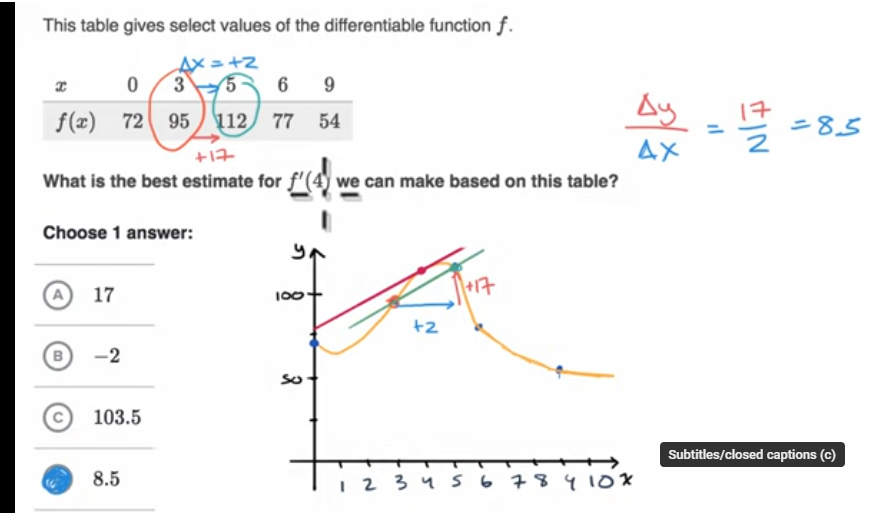
可微性和连续性

 

 

 

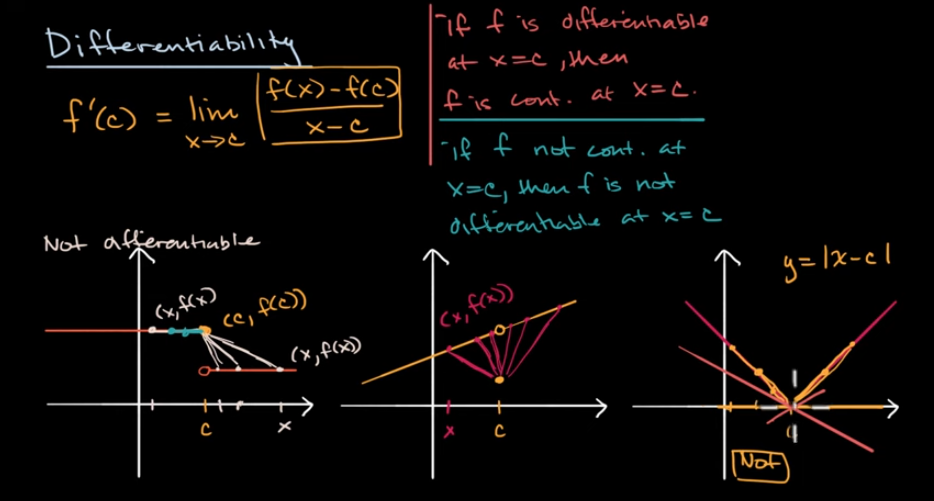
某一点的可微性：图形

例子：

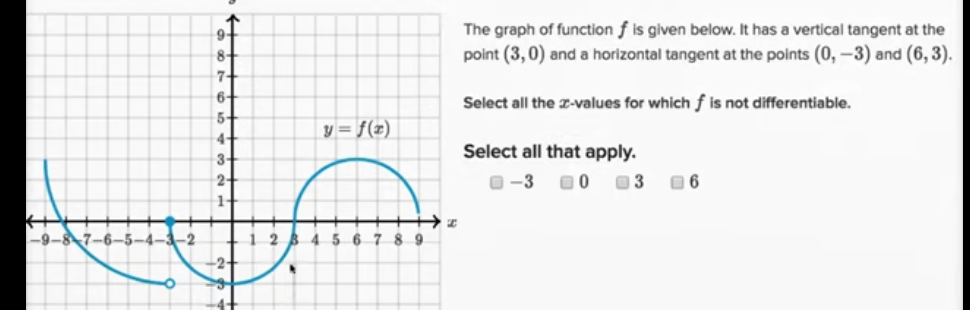
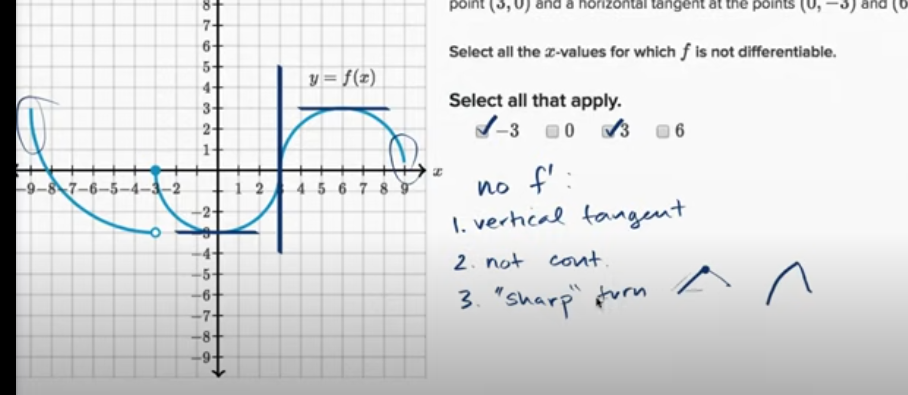
 例子：

 

 

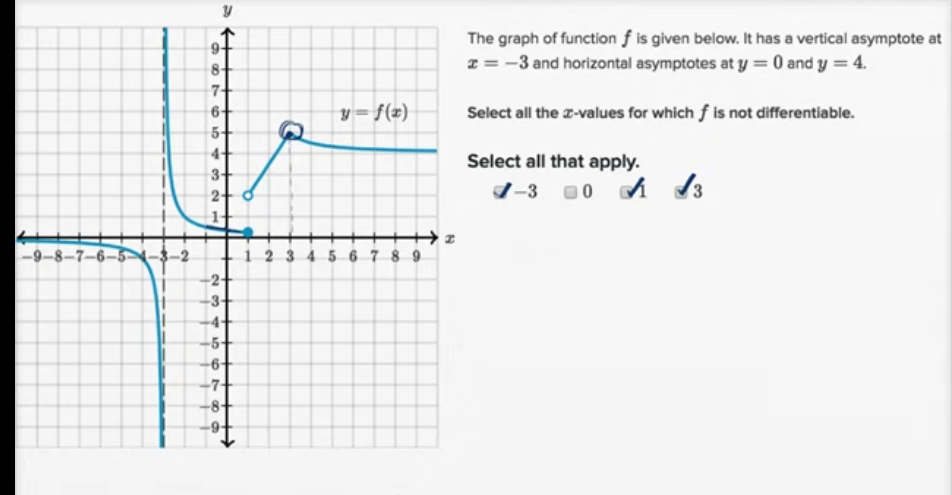
在某一点的可微性：代数的（函数可微）

 

例子：连续不可微

 

 

 

例子：

 

如果一个函数是可微的，那么它也是连续的。这个性质在处理函数时非常有用，因为如果我们知道一个函数是可微的，我们立刻就知道它也是连续的。

 

 

 

幂律

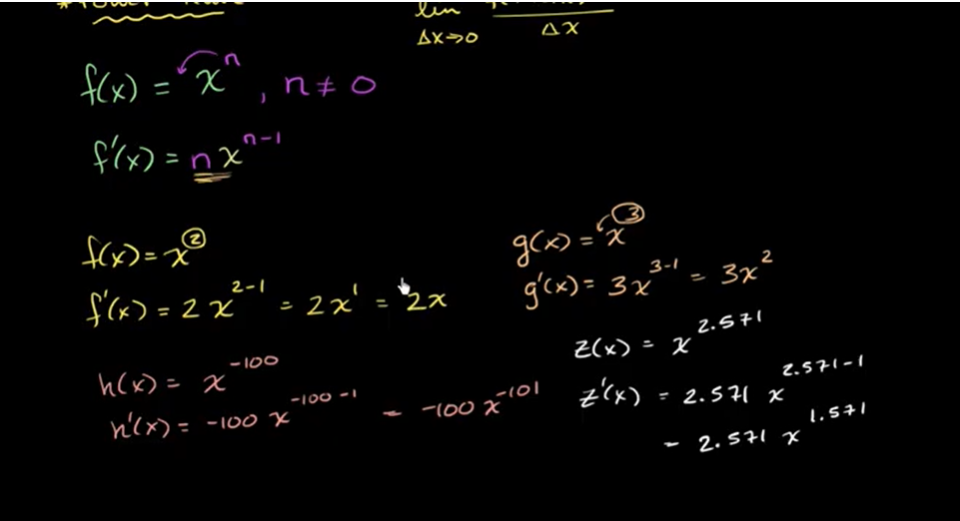
 例子：

 

幂律（负幂和分数幂）

 

 

幂律（重写表达式）

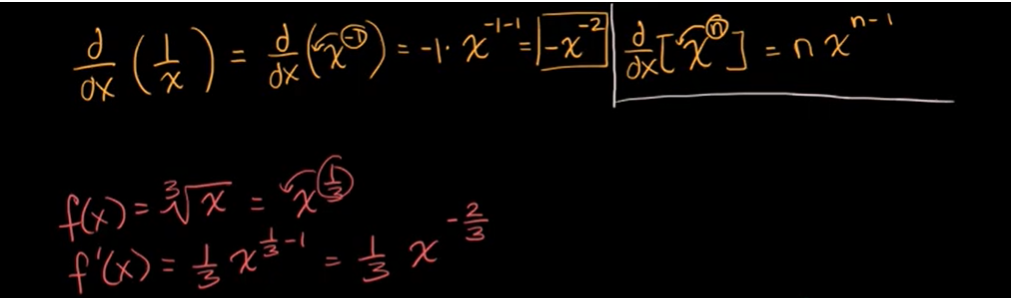
 例子：

 

 

 

 

 

 

 

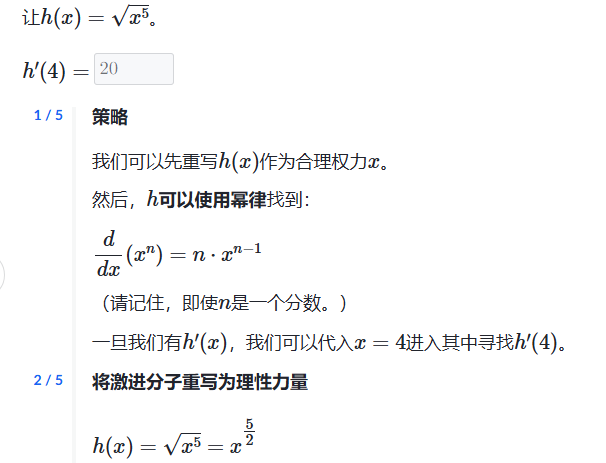
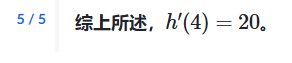
3.基本导数规则

n不可以为0，等于0他的斜率是直线。斜率就是0了

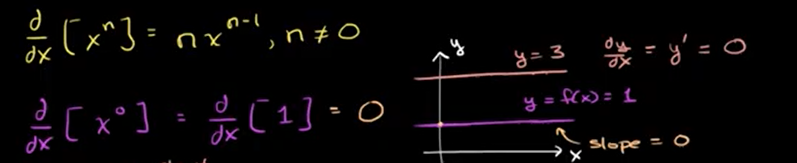
 方式

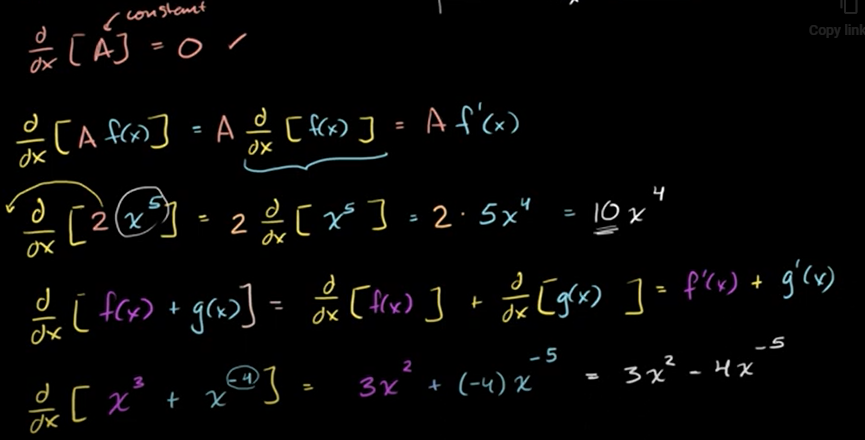
 常数的导数是0

 

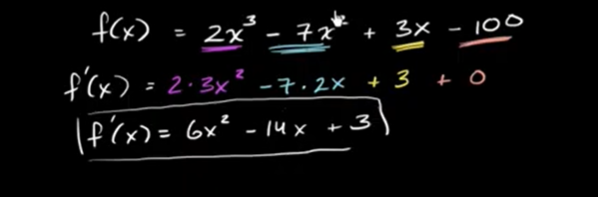
基本导数规则：求误差

基本导数规则：表格

 

 

 

 

区分多项式

 

 

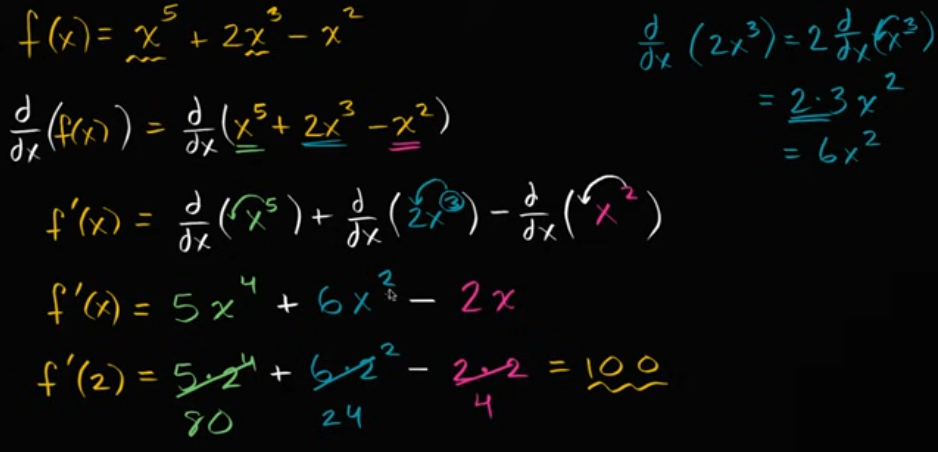
区分整数幂（正负混合）

 

多项式的正切

 

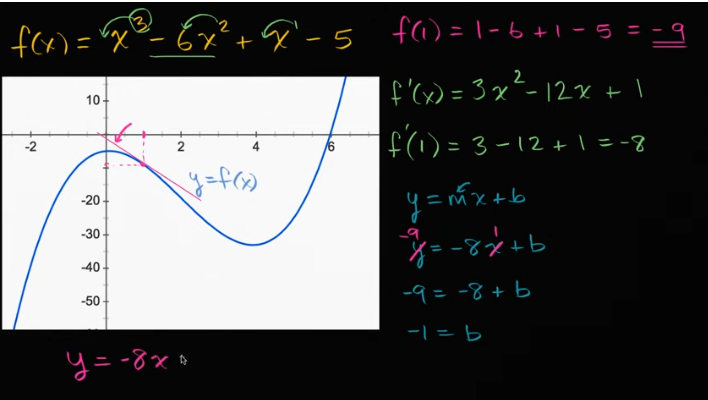
重要

 

 

例子：

 

 

 

例子：

 

 

 

 

 

sin(x) 和 cos(x) 的导数

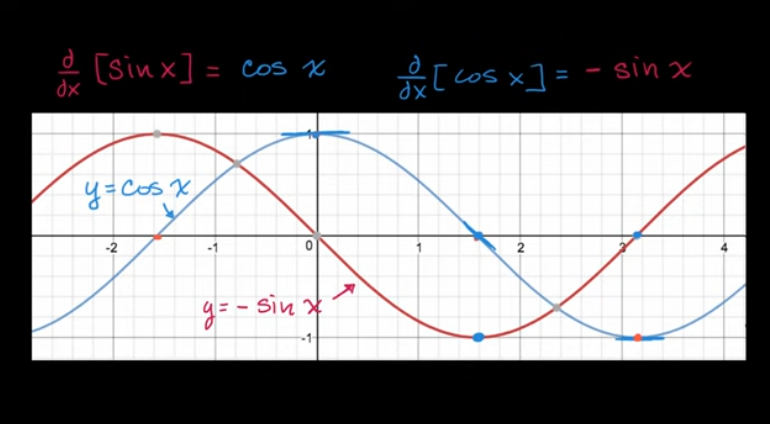
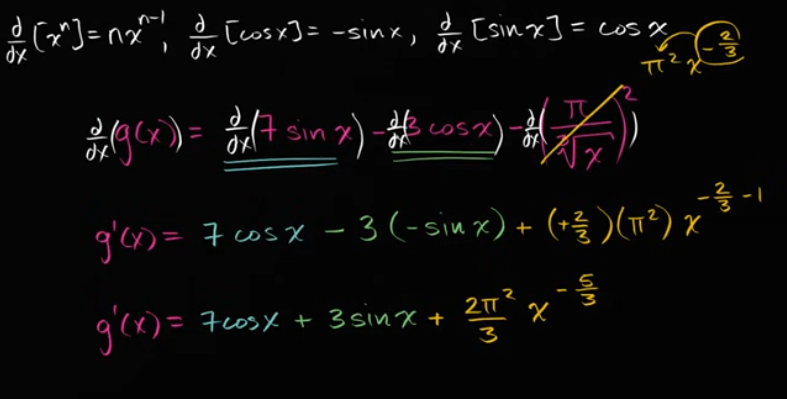
 例子“

 

 

 

公式

 

 

 

 

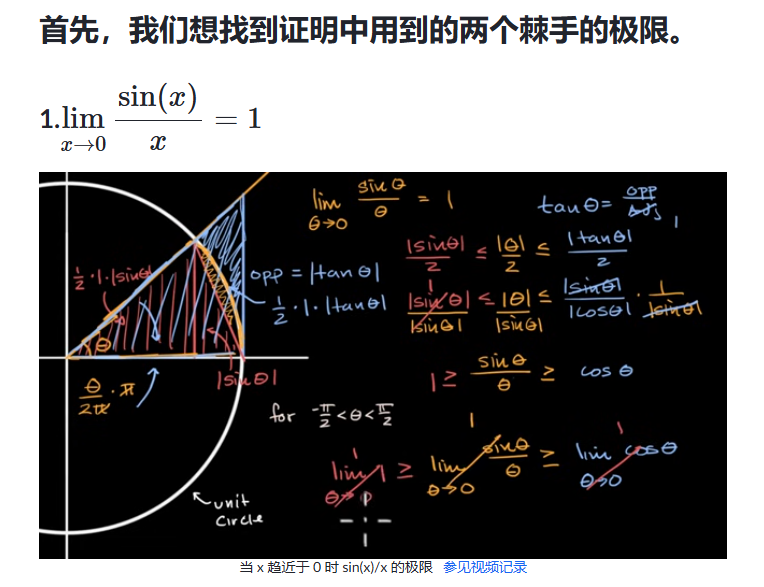
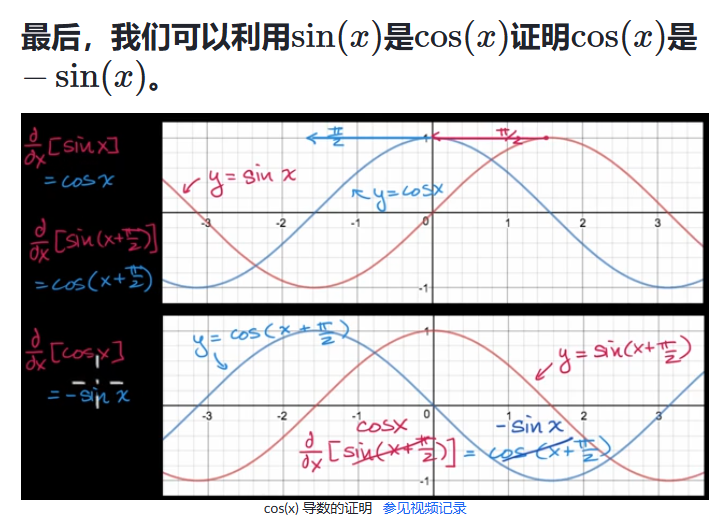
𝑒ˣ 的导数

 

 

 

ln(x) 的导数

 

例子：

 

 

产品规则（乘积法则）

 

 

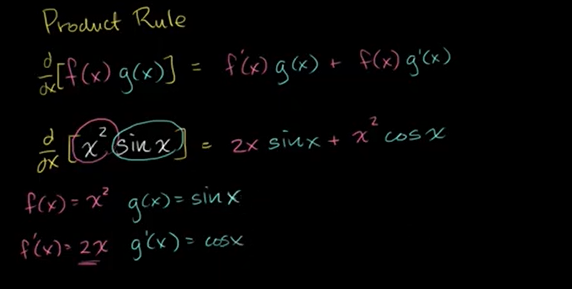
差异化产品

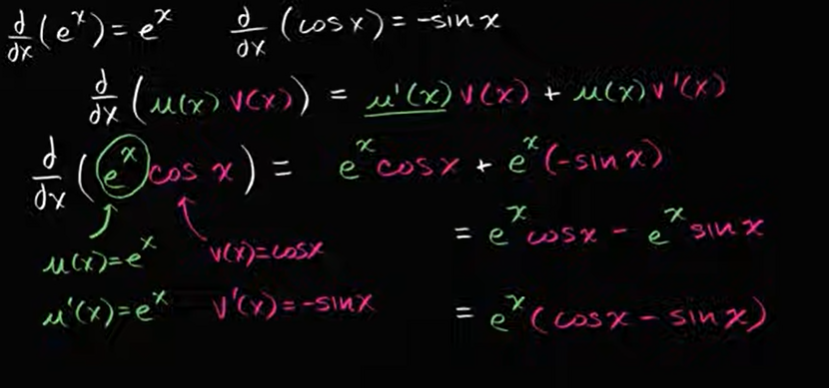
 例子：

 

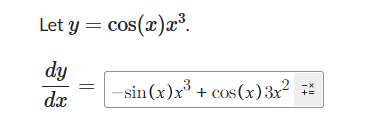
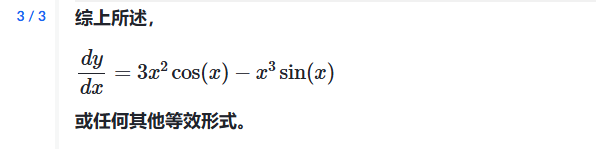
示例：带表的乘积规则

 

示例：混合隐式和显式的乘积规则

 

 

 

 

 

 

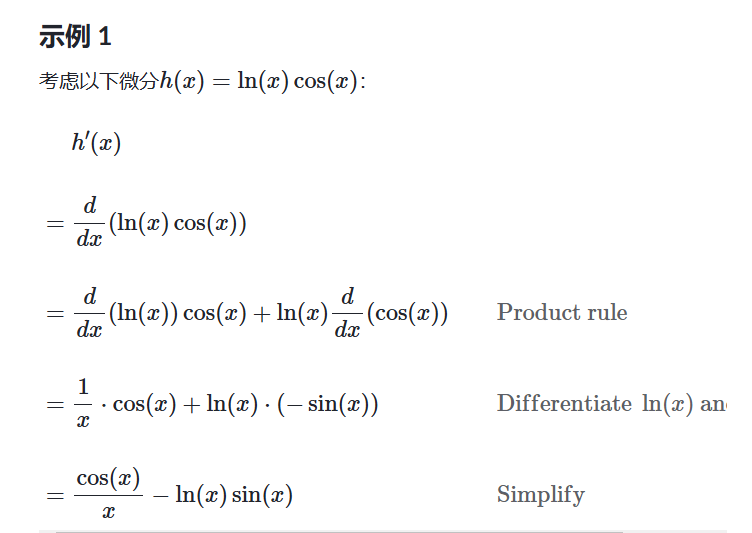
商法则

 

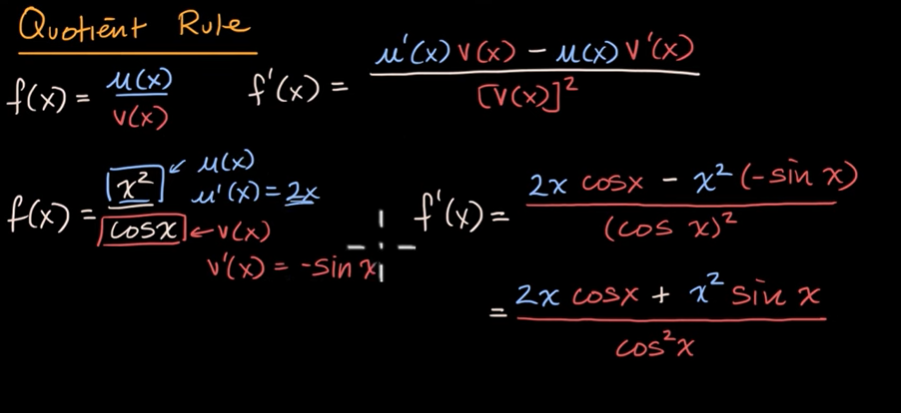
示例：带表格的商法则

 

有理函数的区分

 

 

 

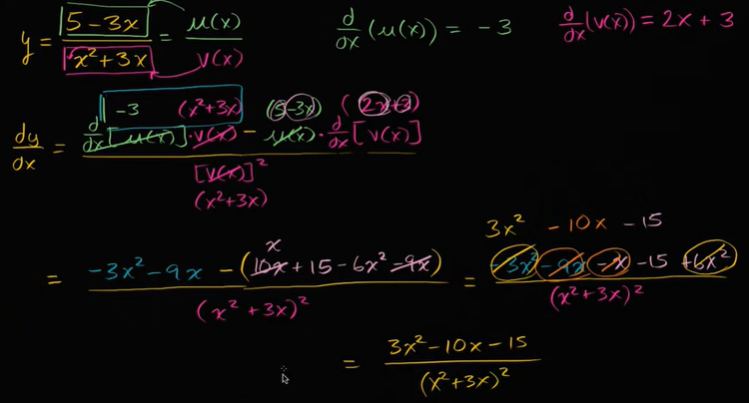
tan(x) 和 cot(x) 的导数

 

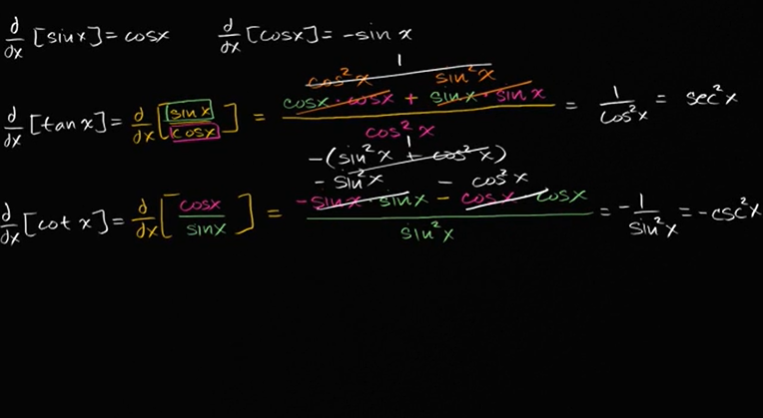
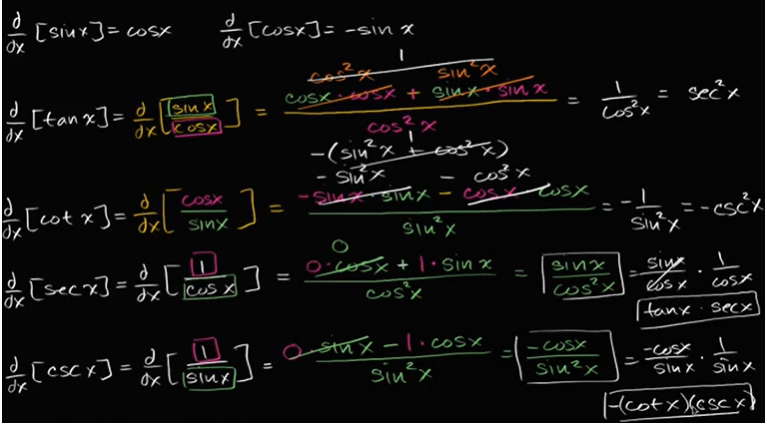
sec(x) 和 csc(x) 的导数