浅谈树链剖分

树链剖分

定理

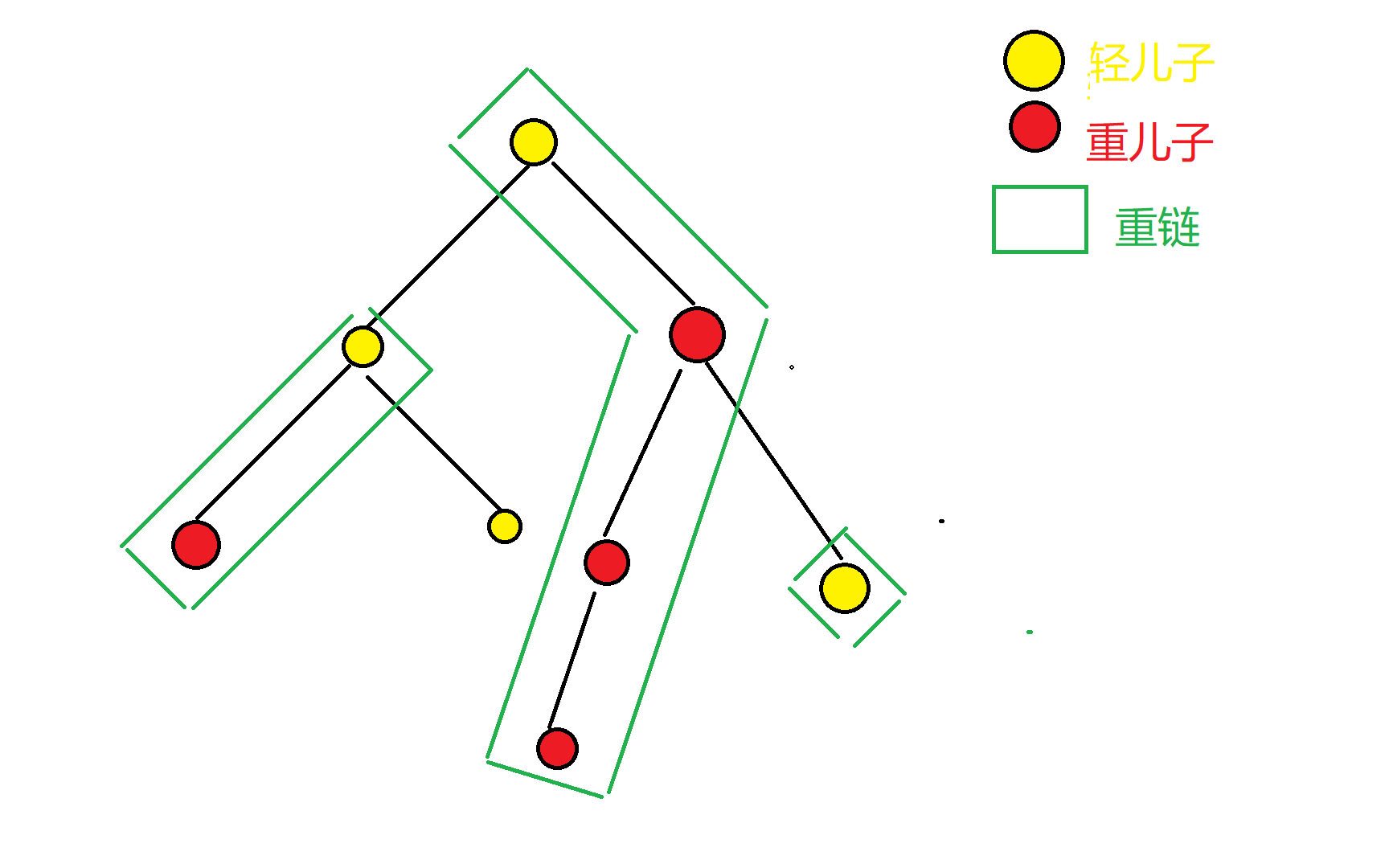
• 重儿子：一个节点所有儿子中，子树大小最大的儿子即为重儿子，如有多个，任取一个即可。
• 轻儿子：除了重儿子外的所有儿子。
• 重边：父节点 \(\to\) 重儿子的边。
• 重链：由重边构成的极大链。
  如以下图。
  

过程

\(dfs\) 序：优先遍历重儿子，这样就可以保证重链上所有点的编号连续。

如下图，蓝色数字即为求完 \(dfs\) 序后所有点的编号。

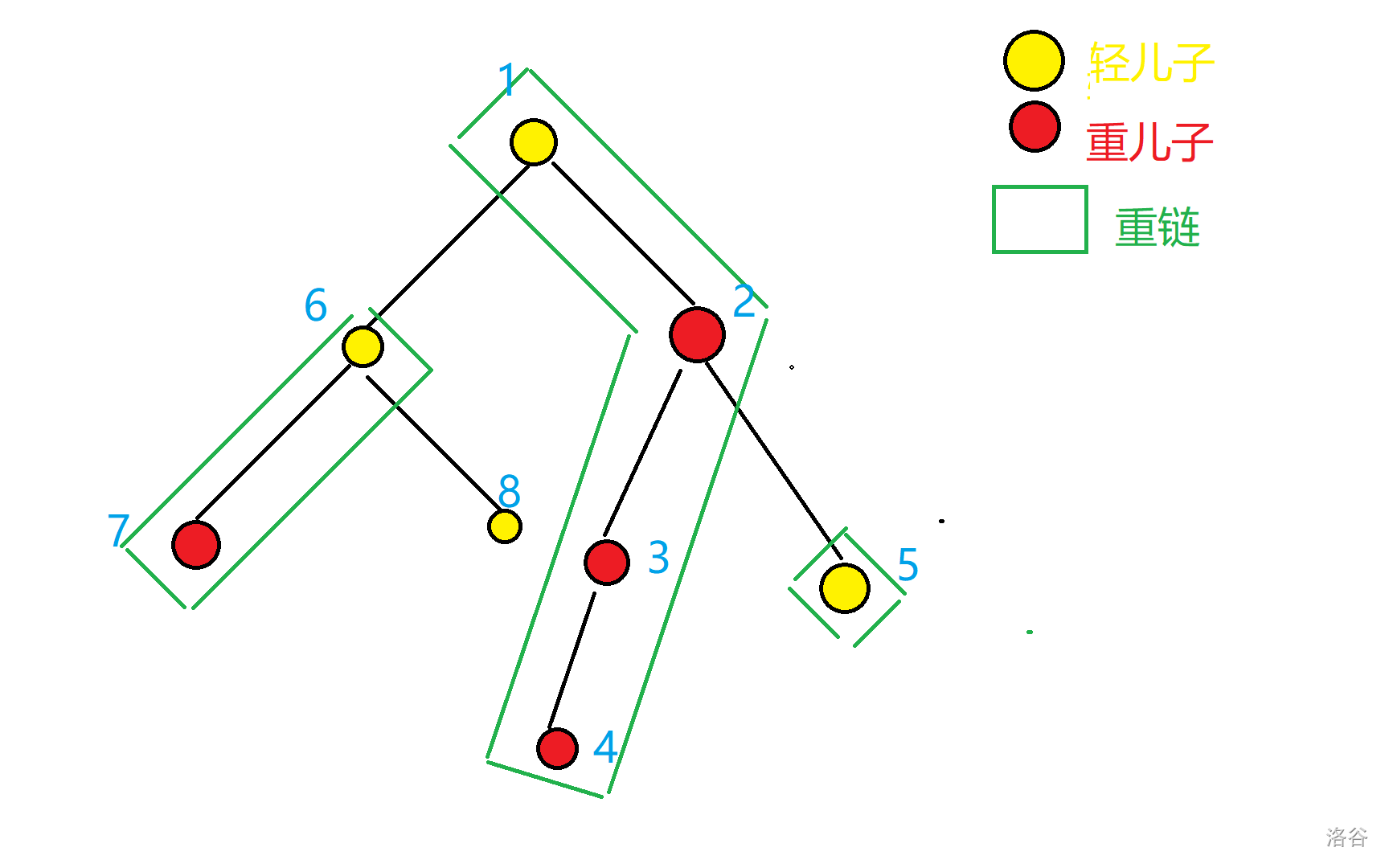
求完 \(dfs\) 序即将树转化成序列。

定理：树中任意一条路径均可拆分成小于等于 \(\log n\) 条重链，即可拆分成小于等于 \(\log n\) 连续区间。

将一条路径拆分成若干条条重链

这个过程类似于倍增求 \(lca\)。

假设求 \(x, y\) 的若干条重链。

如果 \(f_x > f_y\) 则先将 \(x\) 跳到该节点所在重链的顶部再走到他的父节点上。

如果 \(f_y > f_x\) 则先将 \(y\) 跳到该节点所在重链的顶部在走到他的父节点上。

其中 \(f_i\) 表示节点 \(i\) 所在重链顶端的深度，即该节点在树的第几层。

最后一定会走到同一条重链上。

以上操作可以用线段树/分块/Splay 来维护。

例题

\(\mathcal Preface\)

题目传送门

\(\mathcal Solution\)

• 操作 \(\mathit{1 \sim 2}\)：即用前述的树链剖分的思想。
• 操作 \(\mathit{3 \sim 4}\)：即把 \(dfs\) 序的一段连续区间求和或修改。

维护就与此题类似。

\(\mathcal Code\)

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>
#include <cmath>
#include <sstream>
#include <set>
#include <unordered_set>
#include <map>
#include <unordered_map>

#define x first
#define y second
#define IOS ios::sync_with_stdio(false)
#define cit cin.tie(0)
#define cot cout.tie(0)

using namespace std;

typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;

const int N = 100010, M = 200010, MOD = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const LL LLINF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-8;

int n, m, root, mod;
int w[N], h[N], e[M], ne[M], idx;
int id[N], nw[N], cnt;
int dep[N], sz[N], top[N], fa[N], son[N];
struct Node
{
	int l, r;
	LL add, sum;
}tr[N * 4];

void add(int a, int b)
{
	e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void dfs1(int u, int father, int depth)
{
	dep[u] = depth, fa[u] = father, sz[u] = 1;
	for (int i = h[u]; ~i; i = ne[i])
	{
		int j = e[i];
		if (j == father) continue;
		dfs1(j, u, depth + 1);
		sz[u] += sz[j];
		if (sz[son[u]] < sz[j]) son[u] = j;
	}
}

void dfs2(int u, int t)
{
	id[u] = ++ cnt, nw[cnt] = w[u], top[u] = t;
	if (!son[u]) return;
	dfs2(son[u], t);
	for (int i = h[u]; ~i; i = ne[i])
	{
		int j = e[i];
		if (j == fa[u] || j == son[u]) continue;
		dfs2(j, j);
	}
}

void pushup(int u)
{
	tr[u].sum = (tr[u << 1].sum + tr[u << 1 | 1].sum) % mod;
}

void pushdown(int u)
{
	auto &root = tr[u], &left = tr[u << 1], &right = tr[u << 1 | 1];
	left.add = (left.add + root.add) % mod, left.sum = (left.sum + (left.r - left.l + 1ll) * root.add) % mod;
	right.add = (right.add + root.add) % mod, right.sum = (right.sum + (right.r - right.l + 1ll) * root.add) % mod;
	root.add = 0;
}

void build(int u, int l, int r)
{
	if (l == r) tr[u] = {l, r, 0, nw[r]};
	else
	{
		tr[u] = {l, r};
		int mid = l + r >> 1;
		build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
		pushup(u);
	}
}

void modify(int u, int l, int r, int d)
{
	if (tr[u].l >= l && tr[u].r <= r)
	{
		tr[u].add = (tr[u].add + d) % mod;
		tr[u].sum = (tr[u].sum + (tr[u].r - tr[u].l + 1ll) * d) % mod;
	}
	else
	{
		pushdown(u);
		int mid = tr[u].l + tr[u].r >> 1;
		if (l <= mid) modify(u << 1, l, r, d);
		if (r > mid) modify(u << 1 | 1, l, r, d);
		pushup(u);
	}
}

LL query(int u, int l, int r)
{
	if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
	
	pushdown(u);
	int mid = tr[u].l + tr[u].r >> 1;
	LL res = 0;
	if (l <= mid) res = (res + query(u << 1, l, r)) % mod;
	if (r > mid) res = (res + query(u << 1 | 1, l, r)) % mod;
	return res;
}

void updata1(int u, int v, int k)
{
	while (top[u] != top[v])
	{
		if (dep[top[u]] < dep[top[v]]) swap(u, v);
		modify(1, id[top[u]], id[u], k);
		u = fa[top[u]];
	}
	if (dep[u] < dep[v]) swap(u, v);
	modify(1, id[v], id[u], k);
}

LL query1(int u, int v)
{
	LL res = 0;
	while (top[u] != top[v])
	{
		if (dep[top[u]] < dep[top[v]]) swap(u, v);
		res = (res + query(1, id[top[u]], id[u])) % mod;
		u = fa[top[u]];
	}
	if (dep[u] < dep[v]) swap(u, v);
	res = (res + query(1, id[v], id[u])) % mod;
	return res;
}

void updata2(int u, int k)
{
	modify(1, id[u], id[u] + sz[u] - 1, k);
}

LL query2(int u)
{
	return query(1, id[u], id[u] + sz[u] - 1);
}

void solve()
{
	cin >> n >> m >> root >> mod;
	for (int i = 1; i <= n; i ++ ) cin >> w[i];
	
	memset(h, -1, sizeof h);
	for (int i = 1; i < n; i ++ )
	{
		int a, b;
		cin >> a >> b;
		add(a, b), add(b, a);
	}
	
	dfs1(root, -1, 1);
	dfs2(root, root);
	build(1, 1, n);

	while (m -- )
	{
		int op, u, v, k;
		cin >> op >> u;
		if (op == 1)
		{
			cin >> v >> k;
			updata1(u, v, k);
		}
		else if (op == 2)
		{
			cin >> v;
			cout << query1(u, v) << endl;
		}
		else if (op == 3)
		{
			cin >> k;
			updata2(u, k);
		}
		else cout << query2(u) << endl;
	}
}

int main()
{
	IOS;
	cit, cot;
	int T = 1;
//	cin >> T;
	while (T -- ) solve();
	return 0;
}