笔记_第二章_02

随机变量：设随机试验的样本空间为S = {e}，X = X(e) 是定义在样本空间S上的实值单值函数，即称X = X(e)为随机变量（例如：抛n次硬币出现3次正面，记做{X=3}，对于样本有集合A={HHT,HTH,THH},这就是一个事件，即{X=2}时事件A的概率为P(A)=P(X=3)。）

　　　　离散型随机变量：取值有限多个或者可列无限多个（后者的意思：取值可充满某一区间。例如：某一昼夜，某一城市呼叫120的次数）

　　　　　　　　分布律：

　　　　　　常见的离散型随机变量：

　　　　　　　　　　　　　　　　　1、（0-1）两点分布     X~(1,p)

　　　　　　　　　　　　　　　　    2、伯努利试验得到的 二项分布   （n = 1时，即为（0-1）分布）X ~ (n,p)

　　　　　　　　　　　　　　　　　　　　　　　　二项分布：实验n次，m次成功

　　　　　　　　　　　　　　　　　　　　　　　　几何分布：实验n次，n-1次失败，第n次成功

　　　　　　　　　　　　　　　　　　　　　　　　超几何分布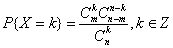：与二项分布不同，二项分布无放回抽取，几何分布有放回抽取。

　　　　　　　　　　　　　　　　　3、泊松分布：　　　X ~ P(入)    

　　　　　　　　　　　　　　　　　　　　　　　　这里有一篇很好的文章“如何理解泊松分布”

　　　　　　　　　　　　　　　　　　　　　　　　总之，我们可以通俗的认为它是二项分布的逼近，当二项分布中p很小时，分布曲线拟合性较高

　　随机变量的分布函数：（用来表示非离散型随机变量的概率）设X是一个随机变量，x是任意实数，函数 ，称为X的分布函数。

　　　　　　　　　　　　　　　　对于任意实数x1，x2，x1<x2，有P{x1<X<=x2}=P{X<=x2}-P{X<=x1}=F(x1)-F(x2) 

　　　　连续型随机变量：对于随机变量X的分布函数F（x），存在非负函数f（x），对于任意实数有：      （注意求导可以互相求出）

　　　　　　　　　　称X为连续型随机变量，f(x)称为X的概率密度函数（概率密度），F(x)为分布函数。

　　　　　　　　　　重要的连续型随机变量：

　　　　　　　　　　　　　　　　1、均匀分布 X在区间（a，b）上均匀分布，即区间内任意等长度的子区间内的可能性相同 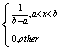 X~U(a，b)

　　　　　　　　　　　　　　　　2、指数分布 密度函数存在指数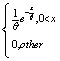 

　　　　　　　　　　　　　　　   3、正态分布（高斯分布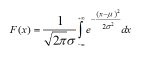） 6越大越矮胖，当时，称为标准正态分布 这里有一篇关于正态分布的文章，有兴趣可以看下：“传送门”

随机变量的函数分布：（可理解为求复合函数的概率密度）

2018-08-03