关于排序
排序
目录 Content
- 概述
- 计数排序(桶排)
- 冒泡排序
- 插入排序
- 选择排序
- 归并排序
- 快速排序
- 其他排序
- 总结
参考资料:OI-Wiki排序
Part 1 概述
排序是一种让若干无序的(不满足某种排序规则的)元素变得有序的方法。
排序算法种类很多,优点各自不同,但最基本的操作几乎一样——交换(swap)
排序算法的应用广泛,是许多算法中一个必须的步骤(比如在贪心中)。
对于排序算法,它的生命线首先就是时间复杂度与稳定性,其次是空间复杂度
Part 2 计数排序
这是最方便于理解的排序算法。它通过建立一个计数数组,统计每个元素出现次数。利用每个元素本身的大小关系进行排序。
过程如下:
- 建立数组
- 遍历每一个元素,统计出现次数
- 从小到大遍历数组,对于每一个非空的元素,输出对应个数。
动图:图源OI-wiki
时空复杂度
时间复杂度\(O(n+w)\),其中w是值域大小,这是输出的时间复杂度。
空间复杂度\(O(w)\)
优点
- 实现简单,易于理解
- 时间复杂度较好
缺点
- 值域大时空间复杂度高,浪费度高
问题 可不可以离散化呢?离散化本身就需要排序,显然为了排序而排序是肯定不划算的。
- 不适用于所有数据类型。适配其他类型可能需要哈希,反而浪费。
实现
const int W=10005;//值域
const int N=10005;//数量
int cnt[W],n,num[N];
void counting_sort(){
int maxn=0;
for(int i=1;i<=n;i++){
cnt[num[i]]++;
maxn=max(maxn,num[i]);
}
for(int i=1;i<=maxn;i++){
for(int j=1;j<=cnt[i];j++)cout<<i<<" ";
}
return;
}
Part 2 冒泡排序
冒泡排序(英语:Bubble sort)是一种简单的排序算法。由于在算法的执行过程中,较小的元素像是气泡般慢慢「浮」到数列的顶端,故叫做冒泡排序。
过程
它的工作原理是每次检查相邻两个元素,如果前面的元素与后面的元素满足给定的排序条件,就将相邻两个元素交换。当没有相邻的元素需要交换时,排序就完成了。
时空复杂度
平均时间复杂度\(O(n^2)\)空间复杂度\(O(n)\)
这个算法是稳定的。
在慢慢将较大数放到后面,较小数放到前面的过程中,可以想像,在最坏情况下:
- 第一次排序一定会把最大的数放到最后,因为没有数比他更大
- 第二次一定会把第二大的放在第二位...
如此循环,每一次遍历至少都会复位一个元素,故最坏时间复杂度为\(O(n^2)\)
优点
- 实现简单,易于理解
缺点
- 慢
实现
// OI-Wiki Version
// 假设数组的大小是n+1,冒泡排序从数组下标1开始
void bubble_sort(int *a, int n) {
bool flag = true;
while (flag) {
flag = false;
for (int i = 1; i < n; ++i) {
if (a[i] > a[i + 1]) {
flag = true;
int t = a[i];
a[i] = a[i + 1];
a[i + 1] = t;
}
}
}
}
Part 3 插入排序
插入排序(英语:Insertion sort)是一种简单直观的排序算法。它的工作原理为将待排列元素划分为「已排序」和「未排序」两部分,每次从「未排序的」元素中选择一个插入到「已排序的」元素中的正确位置。
一个与插入排序相同的操作是打扑克牌时,从牌桌上抓一张牌,按牌面大小插到手牌后,再抓下一张牌。 OI-wiki
过程如下:
- 建立"已排序"集合,最初这个集合里没有数。
- 遍历每一个"未排序"的数。
- 对于每一个未排序的数,找到“已排序“集合里比他大的第一个数并把这个未排序的元素插入在这个数之前。
- 循环往复,直到没有未排序的数。
时空复杂度
平均时间复杂度\(O(n^2)\)空间复杂度\(O(n)\)
这个算法是稳定的。
动图:图源OI-wiki
为什么不用二分找到位置?这样可不可以把一个n化成log?
答:想得美。确实可以二分找到应该插入的位置,可是你要如何插入呢?插入操作使得其必须遍历以腾出空间。即使是STl Vector的insert方法也不是\(O(1)\)的
优点
- 实现简单,易于理解
缺点
- 慢
实现
void InsertSort(int a[], int n)
{
for(int i= 1; i<n; i++){
if(a[i] < a[i-1]){//若第 i 个元素大于 i-1 元素则直接插入;反之,需要找到适当的插入位置后在插入。
int j= i-1;
int x = a[i];
while(j>-1 && x < a[j]){ //采用顺序查找方式找到插入的位置,在查找的同时,将数组中的元素进行后移操作,给插入元素腾出空间
a[j+1] = a[j];
j--;
}
a[j+1] = x; //插入到正确位置
}
}
}
Part 4 选择排序
选择排序是一种简单直观的排序算法。它的工作原理是每次找出第i小的元素(也就是还没有排序数组中最小的元素),然后将这个元素与数组第i个位置上的元素交换。
时空复杂度
平均时间复杂度\(O(n^2)\)空间复杂度\(O(n)\)
这个算法是稳定的。
动图:图源OI-wiki
优点
- 实现简单,易于理解
缺点
- 慢
实现
// OI-Wiki Version
void selection_sort(int* a, int n) {
for (int i = 1; i < n; ++i) {
int ith = i;
for (int j = i + 1; j <= n; ++j) {
if (a[j] < a[ith]) {
ith = j;
}
}
std::swap(a[i], a[ith]);
}
}
Part 5 归并排序
归并排序是一种高效的排序算法。
过程:
- 将原数组分成左右两个部分
- 递归地再次向下对左右两个部分进行排序
- 将原数组合并起来(每一次将两边最小的一个复制过去)并复制到一个辅助数组中
- 将辅助数组复制回原序列
该算法的核心是如何合并左右两个已经排序的数组。
基本过程是:
- 设i,j,k分别为前段的头、后段的头、当前位于辅助数组中的位置
即i=k=l,j=mid
- 若当前后段为空或者前段非空且前段的最小值小于后段的最小值,那么就把前段的当前位置复制到复制辅助数组中当前k的位置,并把前一段的头指针后移一位。
- 否则就把后段的当前位置复制到辅助数组中当前k的位置,并把后一段的头指针后移一位。
- 将辅助数组的指针k后移一位。
时空复杂度
平均时间复杂度\(O(n log n)\)空间复杂度\(O(n)\)
这个算法是稳定的。
优点
- 快
- 实现简单
缺点
- 不易理解
实现
// OI-wiki version
void merge(int l, int r) {
if (r - l <= 1) return;
int mid = l + ((r - l) >> 1);
merge(l, mid), merge(mid, r);
for (int i = l, j = mid, k = l; k < r; ++k) {
if (j == r || (i < mid && a[i] <= a[j]))
tmp[k] = a[i++];
else
tmp[k] = a[j++];
}
for (int i = l; i < r; ++i) a[i] = tmp[i];
}
逆序对
逆序对是形如\((i,j)\)且其中\(i<j,a_i>a_j\)的有序数对。
只需要把ans+=mid-i+1添加在a[j++]后面即可
Tips:
mid-i+1代表着什么?
就是从i到中间的一段里面的元素数量。
为什么是这一段呢?因为前、后段都已经排序,若a[i]>a[j]意味着,i及其以后直到mid的元素都大于a[j]因此将会有mid-i+1个关于a[j]的逆序对形成。然而这次判断之后a[j]就被直接跳过了,所以必须现在加上mid-i+1。
Part 6 快速排序
快速排序是一种快速的排序方法。但他是不稳定的。
快速排序有多种实现方法。但是基本思想是:
- 随机取一个基准元素,将序列划分为几个部分
- 进行调整,看看元素是否放对了位置
- 递归到两边继续排序
可见,快速排序是分治思想的一个应用。
由于快速排序的不稳定性,朴素的快速排序可能会被特殊数据卡到\(O(n^2)\)
我们在这里只讲一种优化版本,三路快速排序。
其实,三路快速排序也有许多实现方式,这里选了比较容易理解的一种
其基本实现过程:
- 随机选定一个基准
- 设置指针
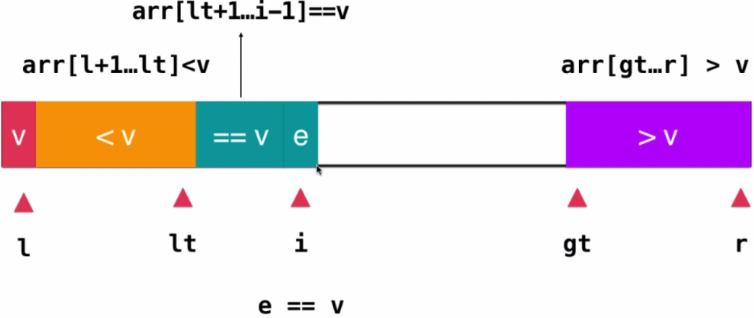
\(lt=\)最后一个小于基准的元素,\(rt=\)第一个大于基准的元素,\(i=\)当前操作数
\(l=\)左边界,\(r=\)右边界
- 对于每一个k指向的元素,考虑如下情况:
注意:原图来自@涛少&。在此基础上进行了编辑。图中gt=rt
- 这个元素等于基准:
那么只需要移动到下一个元素即可,不需要交换。如图所示:
- 这个元素小于基准:
那么将lt+1与k交换,之后把lt++,i++。如图所示:
- 这个元素大于基准:
那么将rt-1和k交换,之后把rt--。如图所示:
- 直到rt和i重合时结束。但是此时l的位置上还有基准元素没有归位,所以只要交换l和lt就好
- 最后递归到两边继续快排
时空复杂度
平均时间复杂度\(O(n log n)\)
最坏时间复杂度\(O(n^2)\)
空间复杂度\(O(n)\)
由于其可能交换两个相同的元素,所以是不稳定的。
优点
- 快
缺点
- 不易理解
- 不稳定
实现
//@涛少&的代码
template<typename T>
void __quickSort3Ways (T arr[], int left, int right)
{
if(right <= left) return;//edit
std::swap(arr[left], arr[std::rand() % (right - left + 1) + left]); // 随机化找到一个元素作为"基准"元素
T v = arr[left];
int lt = left; // 将<v的分界线的索引值lt初始化为第一个元素的位置(也就是<v部分的最后一个元素所在位置)
int gt = right + 1; // 将>v的分界线的索引值gt初始化为最后一个元素right的后一个元素所在位置(也就是>v部分的第一个元素所在位置)
int i = left + 1; // 将遍历序列的索引值i初始化为 left+1
while (i < gt) { // 循环继续的条件
if (arr[i] < v) {
std::swap(arr[i], arr[lt + 1]); // 如果当前位置元素<v,则将当前位置元素与=v部分的第一个元素交换位置
i++; // i++ 考虑下一个元素
lt++; // lt++ 表示<v部分多了一个元素
}
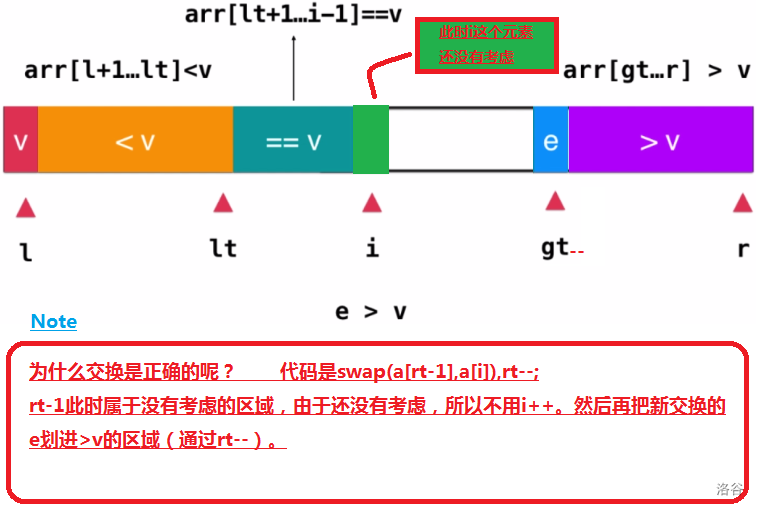
else if (arr[i] > v) { // 如果当前位置元素>v,则将当前位置元素与>v部分的第一个元素的前一个元素交换位置
std::swap(arr[i], arr[gt - 1]); // 此时i不用动,因为交换过来的元素还没有考虑他的大小
gt--; // gt-- 表示>v部分多了一个元素
}
else { // 如果当前位置元素=v 则只需要将i++即可,表示=v部分多了一个元素
i++;
}
}
std::swap(arr[left], arr[lt]); // 上面的遍历完成之后,将整个序列的第一个元素(也就是"基准"元素)放置到合适的位置
// 也就是将它放置在=v部分即可
__quickSort3Ways<T>(arr, left, lt - 1); // 对<v部分递归调用__quickSort3Ways函数进行三路排序
__quickSort3Ways<T>(arr, gt, right); // 对>v部分递归调用__quickSort3Ways函数进行三路排序
}
template<typename T>
void quickSort3Ways (T arr[], int count)
{
std::srand(std::time(NULL)); /* 种下随机种子 */
__quickSort3Ways<T>(arr, 0, count-1); /* 调用__quickSort3Ways函数进行三路快速排序 */
}
Part 7 其他排序
正常的:
- 锦标赛排序 稳定\(O(n log n)\)
- 希尔排序 不稳定最优\(O(n)\)
- 堆排序 稳定\(O(n log n)\)
其中有两个排序既稳定,复杂度也低(况且堆排序还实现简单priority_queue)
为什么不常用呢?
首先,锦标赛排序实现复杂思想不易理解,不适合用于OI等场景。
其次,实际上他们的实际速度在计算机上会比快速排序慢。
资料:C++ 性能榨汁机之局部性原理 - I'm Root lee !
乱搞的:
- 无限猴子排序 最好O(n)最坏O(∞)
Part 8 总结
在数据值域小时建议桶排,其他请用归并或快速。
EOF
感谢观看。\(\huge QwQ\)
本文来自博客园,作者:haozexu,转载请注明原文链接:https://www.cnblogs.com/haozexu/p/17488406.html






 浙公网安备 33010602011771号
浙公网安备 33010602011771号