从马尔科夫链到马尔科夫决策过程：概率控制的数理基石

在信息爆炸与不确定性日益增强的现代社会，如何在随机环境下做出理性决策成为诸多领域的核心问题。从天气预测、股市分析、机器人路径规划，到医疗诊断、语言模型的自然生成，背后都有一个共同的数学支柱：马尔科夫理论。从最初描述随机状态转移的马尔科夫链，到考虑行动选择与收益优化的马尔科夫决策过程（MDP），这一理论架构已经成为人工智能、运筹优化、控制论与金融工程等学科的共通语言。它不仅揭示了“当前状态决定未来”的简洁哲理，更让人们在不确定中找到了“概率中的秩序”。

“The future is independent of the past, given the present.”
—— Andrey A. Markov

“只要知道现在，我们就可以忘记过去而预测未来。”这不仅是马尔科夫性质的本质表达，也成为许多智能系统决策机制的思想支点。

目录

一、引言：为什么我们关心马尔科夫过程？

无论是自然界中的天气系统、金融市场的涨跌、机器人运动路径的规划，还是人工智能中的策略学习，状态的转移与决策的不确定性都无处不在。为了在这些复杂系统中进行有效建模与推理，人们引入了“马尔科夫性”这一强大假设。

所谓马尔科夫性，是指系统的未来状态只依赖当前状态，而与过去历史无关。这种“无记忆”性质极大地简化了动态系统的建模难度，使我们能够用概率矩阵精确刻画状态之间的跃迁规律。早期，这一思想最初应用于语言学与统计物理，很快又扩展到生物学、运筹学、金融工程、通信编码等领域，成为分析复杂系统的数理基石。

在现代人工智能中，强化学习（Reinforcement Learning）正是建立在马尔科夫决策过程（MDP）之上。智能体如何在不确定环境中逐步学习最优策略？如何在面对未来结果尚未可知的情况下制定最优决策？这正是马尔科夫过程大显身手之处。本文将从最基础的马尔科夫链入手，逐步引出转移概率矩阵、极限行为与稳态分布的概念，进而深入到马尔科夫决策过程的结构要素，并结合前沿应用展示它如何支撑从理论建模到实际智能控制的一整套体系。

二、马尔科夫的生平与学术贡献

安德烈·安德烈耶维奇·马尔科夫（Andrey Andreyevich Markov），1856年出生于俄罗斯图拉省，是19世纪末至20世纪初俄罗斯最杰出的数学家之一。他的研究兴趣涵盖概率论、数论、函数论等多个数学领域，尤其以开创马尔科夫链理论而被誉为现代随机过程理论的奠基人。

马尔科夫早年在圣彼得堡大学学习数学，师从契比雪夫（Pafnuty Chebyshev）与柳比谢夫等人。在学术上，马尔科夫推崇逻辑严谨与形式完备，反对将数学工具用于缺乏理性支持的哲学论证。他终其一生致力于概率论基础的严格化。
1906年，马尔科夫在研究俄文诗歌中元音与辅音交替出现的规律时，首次构造了**“状态转移只依赖当前状态，不依赖历史”的随机过程模型**，即今日所称“马尔科夫链”。这一开创性构想打破了传统独立事件假设的束缚，为后续随机过程理论的发展奠定基础。
马尔科夫的思想影响深远：其学生如安德雷·柯尔莫哥洛夫（Kolmogorov）将其理论进一步推广至连续时间与连续状态空间，发展成完整的概率论公理体系。尽管身处动荡的沙皇俄国和苏联早期，马尔科夫始终坚持学术自由与思想独立，拒绝党派干预学术。

今天，“马尔科夫性”已成为数学、物理、计算机科学、控制工程乃至社会科学的基本假设之一。每当我们在机器学习中谈论马尔科夫决策过程、强化学习或隐马尔科夫模型时，都离不开这位数学家的深远影响。

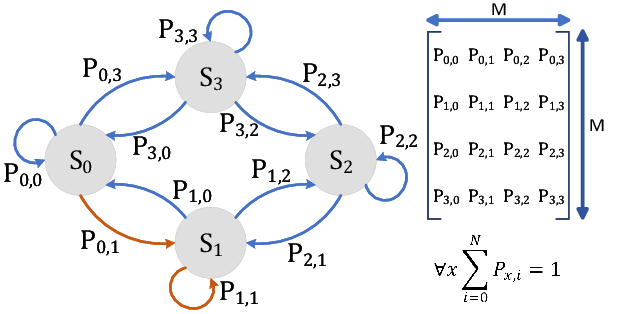
三、马尔科夫链：从状态转移看世界

3.1 定义与基本性质

马尔科夫链是一类离散时间、离散状态的随机过程，满足“无后效性”或“马尔科夫性”：

\[P(X_{n+1} = x | X_n = x_n, X_{n-1} = x_{n-1}, ..., X_0 = x_0) = P(X_{n+1} = x | X_n = x_n) \]

简言之，未来的状态只依赖于当前状态，与过去无关。

3.2 概率转移矩阵

马尔科夫链用一个概率转移矩阵 \(P\) 表示状态之间的跳转概率：

\[P = \begin{bmatrix} P_{11} & P_{12} & \cdots & P_{1n} \\ P_{21} & P_{22} & \cdots & P_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ P_{n1} & P_{n2} & \cdots & P_{nn} \end{bmatrix} \]

其中 \(P_{ij} = P(X_{t+1}=j \mid X_t=i)\)。\(P\) 的每一行之和为 1。

3.3 n步转移概率与极限状态

通过矩阵幂计算 \(P^n\)，可以得到系统经过 n 步后的状态分布。若存在极限矩阵：

\[\lim_{n\to\infty} P^n = \Pi \]

则 \(\pi\) 是稳态分布，满足 \(\pi = \pi P\)。

四、马尔科夫性质的实际应用

马尔科夫性质——即系统的未来状态仅取决于当前状态而非过去的历史——使得复杂动态系统的分析变得高度可 tractable。这一思想被广泛应用于各类实际场景中，为建模、预测和最优控制提供了理论基础。

4.1 金融风险建模

在金融系统中，马尔可夫链被广泛用于建模信用评级转移与市场状态变化。例如，一个企业的信用评级（如AAA、AA、A、BBB 等）可以看作状态空间，在不同时间段可能由于经济形势、财务表现而发生跳转。基于历史评级变动数据，可以构建状态转移概率矩阵，从而估计未来违约概率和期望收益。这种建模为风险管理、资产定价和监管合规提供了量化支撑。

4.2 语音识别与自然语言处理

自然语言中词语的出现具有上下文依赖性，但在建模时常简化为“一阶马尔科夫模型”——即当前词只与前一个词有关。这种简化结构下的语言模型（如 bigram、trigram 模型）广泛应用于语音识别、拼写校正和机器翻译等任务。此外，**隐马尔科夫模型（HMM）**更进一步扩展了马尔科夫性质，广泛用于语音信号状态的分段与识别，是早期语音识别系统的核心。

4.3 交通与排队建模

在交通工程和运营研究中，马尔科夫链广泛用于分析交通状态转移和服务系统的排队行为。比如，在服务窗口系统中（如银行、医院、快餐店），顾客的到达和离开状态满足泊松过程，队列长度的变化可用马尔科夫链分析其稳态分布，从而计算平均等待时间、服务水平等指标。类似地，城市道路网络的拥堵状态变化也常通过马尔科夫链进行建模与预测，有助于动态信号控制与路径推荐。

4.4 图像处理与机器人路径规划

在图像分割与增强中，像素的颜色或纹理特征常被视为状态，其空间关联性可用马尔科夫随机场（MRF）建模，用于生成更平滑、合理的图像区域划分。而在机器人路径规划中，马尔科夫过程用于描述智能体在网格环境中各点的移动概率，从而在面对不确定的地形、障碍和传感误差时，仍能通过策略优化找到最优路径。**部分可观测马尔科夫决策过程（POMDP）**更进一步允许状态不可完全观测，常用于自主驾驶与任务计划系统。

五、马尔科夫决策过程（MDP）：引入决策的链式控制

5.1 定义

马尔科夫决策过程 MDP 是一个四元组：

\[(S, A, P, R) \]

  • \(S\)：状态空间
  • \(A\)：动作空间
  • \(P(s' | s, a)\)：状态转移概率
  • \(R(s, a)\)：即时奖励

5.2 策略与价值函数

  • 策略 \(\pi(a|s)\)：在状态 \(s\) 下采取动作 \(a\) 的概率
  • 状态价值函数：

\[V^{\pi}(s) = \mathbb{E}_\pi\left[ \sum_{t=0}^{\infty} \gamma^t R(s_t, a_t) \right] \]

  • 行为价值函数：

\[Q^{\pi}(s,a) = \mathbb{E}_\pi\left[ \sum_{t=0}^{\infty} \gamma^t R(s_t, a_t) \mid s_0=s, a_0=a \right] \]

5.3 贝尔曼方程与最优性

  • 贝尔曼方程：

\[V^{\pi}(s) = \sum_a \pi(a|s) \left[ R(s,a) + \gamma \sum_{s'} P(s'|s,a) V^{\pi}(s') \right] \]

  • 最优值函数满足：

\[V^*(s) = \max_a \left[ R(s,a) + \gamma \sum_{s'} P(s'|s,a) V^*(s') \right] \]

六、从MDP到现实控制：强化学习与最优策略

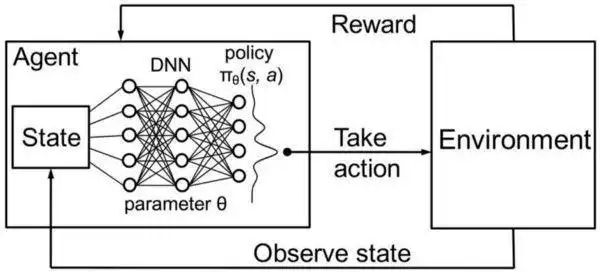
马尔科夫决策过程（MDP）不仅是理论建模工具，更是现实世界中“学习—决策—反馈—优化”循环的基础。在机器人控制、自动驾驶、智能推荐等领域，如何从复杂环境中逐步摸索出最优策略，成为强化学习（Reinforcement Learning）研究的核心问题。

6.1 策略迭代与值迭代

在 MDP 的经典设定中，我们假定状态转移概率 \(P \left(\right. s^{'} \mid s , a \left.\right)\) 与奖励函数 \(R \left(\right. s , a \left.\right)\) 已知。在这种“模型已知”的情境下，最优策略可通过两类迭代算法求解：

  • 值迭代（Value Iteration）：基于贝尔曼最优方程（Bellman Optimality Equation），通过对状态值函数 \(V \left(\right. s \left.\right)\)V(s) 的更新收敛，进而导出最优策略。

\[V_{k + 1} \left(\right. s \left.\right) = \underset{a}{max ⁡} \underset{s^{'}}{\sum} P \left(\right. s^{'} \mid s , a \left.\right) \left[\right. R \left(\right. s , a \left.\right) + \gamma V_{k} \left(\right. s^{'} \left.\right) \left]\right. \]

  • 策略迭代（Policy Iteration）：在当前策略下估计值函数（策略评估），再基于当前值函数改进策略（策略改进），不断交替，直到策略不再变化。

两者的目标都是求出长期累计奖励（期望回报）最大的策略 \(\pi^{*}\)，即在每个状态下选择最优动作。

6.2 强化学习的对偶性

然而，在许多真实环境中，如游戏对战、机器人实验、金融交易中，转移概率 \(P\)P 和奖励函数 \(R\)R 都是不可知的黑箱，此时便进入了强化学习的范畴。强化学习摆脱了对模型的依赖，而是通过与环境交互不断试错、累计经验，最终学得最优策略。

常见方法包括：

  • Q-learning：通过估计状态-动作值函数 \(Q \left(\right. s , a \left.\right)\) 并不断更新，逼近最优策略。

\[Q \left(\right. s , a \left.\right) \leftarrow Q \left(\right. s , a \left.\right) + \alpha \left[\right. r + \gamma \underset{a^{'}}{max ⁡} Q \left(\right. s^{'} , a^{'} \left.\right) - Q \left(\right. s , a \left.\right) \left]\right. \]

  • SARSA：类似于 Q-learning，但更新使用当前策略生成的 \(a^{'}\)，更加保守。
  • DQN（Deep Q-Network）：使用神经网络近似 \(Q \left(\right. s , a \left.\right)\)，让强化学习具备“感知能力”，广泛用于图像处理、Atari 游戏等。

强化学习将传统 MDP 的结构与现代数据驱动方法相结合，使得“最优控制”从数学模型走向了现实世界的智能控制系统。

七、结语：马尔科夫思想的未来演化

从状态的概率跳转，到决策路径的全局优化，马尔科夫理论已不再是纸上模型，而是智能控制的神经中枢。

马尔科夫过程的核心思想——当前状态足以描述未来演化的可能性——正越来越多地体现在实际系统中。从自动驾驶车辆的路径预测，到智能对话系统的意图建模，再到动态金融策略的实时优化，马尔科夫模型正在逐步拓展至更复杂、更高维的应用场景。
未来，随着模型预测控制（MPC）与多智能体系统（MAS）的融合发展，马尔科夫过程将成为系统行为建模与学习的重要桥梁；在脑机接口（BCI）和认知神经科学中，马尔科夫决策过程也可用于建构个体的行为推断和注意力迁移模型，进而实现更加自然的人机协同。
在泛智能时代，马尔科夫思想的演化不仅意味着建模层次的提升，更代表了我们对于不确定性、动态性和最优性这三者关系理解的深化。

参考文献和扩展阅读

为了更深入理解马尔可夫过程与马尔可夫决策过程（MDP）的理论与实践，推荐以下文献与资料：

  1. Puterman, M. L. (2005). Markov Decision Processes: Discrete Stochastic Dynamic Programming.
    被誉为MDP研究的经典之作，系统阐述了策略评估、最优性、迭代方法等核心内容。
  2. Sutton, R. S., & Barto, A. G. (2018). Reinforcement Learning: An Introduction (2nd ed.).
    强化学习领域的权威教材，深入讲解了从动态规划到深度强化学习的演化。
  3. Russell, S., & Norvig, P. (2020). Artificial Intelligence: A Modern Approach (4th ed.).
    本书从AI角度出发，介绍了MDP与不确定性推理在智能体中的重要作用。
  4. David Silver’s Reinforcement Learning Course (UCL, DeepMind).
    https://www.davidsilver.uk/teaching/
    包含强化学习中MDP的精彩讲解与实践算法，适合中高级读者进阶学习。

这些资料将帮助读者从基础理论到实际应用，全面掌握马尔科夫过程的建模、分析与优化策略。

马尔科夫模型已从理论工具演化为智能系统的内核。未来，它将在认知建模、智能控制与人机协同中持续扩展边界，成为连接不确定环境与最优决策的核心桥梁。

posted @ 2025-07-23 06:00  郝hai  阅读(234)  评论(0)    收藏  举报