从哥尼斯堡七桥到图论开端：欧拉的开创性贡献

在浩瀚的数学星河中，有一位横跨分析、数论、拓扑、物理、力学等众多领域的巨擘——莱昂哈德·欧拉（Leonhard Euler）。他不仅以惊人的论文数量和符号规范重塑数学语言，更以逻辑之光照亮科学进程。从哥尼斯堡的一座桥开始，他首次将“结构”而非“度量”作为问题核心，开创了图论与拓扑的先河。在那个尚未有现代数学术语的时代，他用一篇简短论文，将城市游览的趣题转化为一门严谨的学科。这不仅是一次桥梁问题的解答，更是一种全新思维方式的起点。

“欧拉不只是解开了七桥之谜，更架起了从现实走向抽象的第一道桥梁。他用笔触连起了点与线，也连通了数学与世界。”
—— 数学史家克莱因（Felix Klein）

目录

一、引言：通向数学世界的钥匙

在数学的殿堂里，有一位智者的名字被一代又一代科学家敬仰。他用符号重塑思维的逻辑，用公式勾勒宇宙的规律，用抽象的结构化语言为后来的科学发展奠定坚实基础。他，就是被誉为“数学之王”的莱昂哈德·欧拉（Leonhard Euler）。
欧拉不仅是数学史上最伟大的创造者之一，更是将数学推向系统化、现代化的关键人物。他的研究几乎涵盖当时所有主要的数学与物理领域，包括数论、解析几何、微积分、拓扑、图论、复变函数、力学、光学、天文学、流体力学等，留下超过800部著作和论文。这使他成为史上发表论文最多的数学家，至今仍是多个数学分支的命名者与奠基人。
然而，他的贡献不仅在于“数量”，更在于“语言”。函数符号 \(f \left(\right. x \left.\right)\)、欧拉公式 \(e^{i x} = cos ⁡ x + i sin ⁡ x\)、常数 \(e\) 的命名、复数的表达方式……无不出自他之手。他构建了现代数学通用的记号系统，促进了交流，统一了数学语言。
值得玩味的是，这位几乎无所不精的巨匠，其一项具有划时代意义的突破，起源却是一道来自日常生活的趣味谜题——哥尼斯堡七桥问题。一座城市、七座桥、一次日常的散步，催生了图论与拓扑的开端，也揭开了数学研究走向“结构思维”的序幕。正是这扇“桥”，带领我们走进欧拉的世界。

二、生平简述：从巴塞尔走向世界

2.1 少年成才：瑞士巴塞尔的神童

莱昂哈德·欧拉（Leonhard Euler）于1707年4月15日出生在瑞士巴塞尔，家中排行长子。父亲保罗·欧拉是一位路德宗牧师，年轻时曾是数学家雅各布·伯努利的学生，对数学颇有造诣。欧拉从小在家庭熏陶下展现出卓越的逻辑思维与算术才能。虽然最初按照父亲意愿学习神学，但欧拉更倾心于数学与自然哲学。13岁那年，他被送入巴塞尔大学，成为当时最年轻的大学生之一。
在巴塞尔大学，欧拉结识了约翰·伯努利——当时欧洲最杰出的数学家之一。在伯努利的指导下，欧拉每周六前往其家中聆听“私人授课”。伯努利敏锐地意识到这位少年拥有非凡的天赋，不久便放手让欧拉独立探索深奥问题，仅在关键处点拨一二。
17岁时，欧拉完成硕士论文《论声音的传播》，并于20岁凭借另一篇关于航海中使用桅杆的力学论文，成功赢得俄国圣彼得堡科学院的关注。这一举动也正式开启了他波澜壮阔的科学生涯。

2.2 圣彼得堡与柏林：两个学术高峰

1727年，欧拉应伯努利之子丹尼尔·伯努利邀请，前往俄国圣彼得堡科学院担任职员。起初他负责医学工作，但不久即转入数学与物理部门。圣彼得堡科学院当时聚集了大量西欧顶尖学者，为欧拉提供了自由研究与合作的理想环境。
在圣彼得堡期间，欧拉迅速在微积分、流体力学、天文学等领域展现才华。他还受命参与多项军事与工程任务，如舰船建模、炮弹轨道计算、地图制作等，表现出数学在实践中的巨大潜力。1735年，年仅28岁的欧拉便被任命为数学教授。
1741年，欧拉接受普鲁士国王腓特烈大帝的邀请，迁至柏林，出任柏林科学院数学部主任。在柏林的25年中，欧拉不仅成为学院学术核心，还撰写了大量基础性著作，如《无穷小分析导引》《解析函数引论》《力学教程》等，为后人奠定分析与理论力学基础。
此外，他还致力于科普写作，为少年学生编写《给德国王后儿子的信》，以浅显文字讲解力学与天文，被誉为“最通俗的科学读本”。

2.3 晚年与辞世

1766年，欧拉重返圣彼得堡，继续从事数学与物理研究。令人震惊的是，此时他已近全盲，仅凭惊人的记忆力和逻辑推理能力，通过口述方式，每天依旧高产不辍。他的助手根据其指令记录、整理和计算，甚至不需草稿。
在完全失明的17年中，欧拉完成了超过400篇论文和多部重要著作，效率远超常人。1783年9月18日，欧拉在与家人愉快交谈时突发脑溢血，安详辞世，享年76岁。几小时之前，他仍在计算火星轨道。
法国数学家拉格朗日悼念道：“他死了，但他仿佛还活着；他的作品将延续他的思想，跨越世纪。”欧拉的一生，是天才、勤奋与科学精神的完美结合。他不仅塑造了18世纪的数学版图，更为后世留下无可替代的思想遗产。

三、主要贡献纵览：奠定数学帝国

欧拉的成果极为广泛，下表总结其对数学语言、结构与理论的关键贡献：

领域 代表成果 影响
数学语言 使用 \(f(x)\)，推广 \(e\)，定义 \(\pi\)，引入 \(\Sigma\) 奠定现代数学书写与记号系统
分析学 欧拉级数、欧拉恒等式、三角函数展开 推动无穷级数与微积分的发展
数论 欧拉函数 \(\phi(n)\)，欧拉乘积公式 开创解析数论，连接级数与素数
图论/拓扑 七桥问题，欧拉图定义，提出欧拉通路 图论与拓扑学的起点
微分方程 欧拉法、常微分解法、欧拉–拉格朗日方程 数值分析和经典物理模型基础
力学/刚体运动 欧拉角、欧拉方程、欧拉梁理论 工程与刚体动力学基石
组合数学 欧拉数、斯特灵数、拉丁方阵、分割数 丰富现代组合数学与统计建模
天文学/应用数学 轨道计算、潮汐研究、光学解析 奠定应用数学与天体力学体系

欧拉的成就不仅数量惊人，更在于他建立了数学的结构性思维模式，影响持续至今。

四、哥尼斯堡七桥问题：图论的起点

4.1 背景：七桥之谜

18世纪初的普鲁士城市哥尼斯堡（今俄罗斯加里宁格勒），有一道名为普雷戈尔河的河流将城市分为四块陆地。当地修建了七座桥梁连接这四个区域，成为市民休闲散步的一大特色。

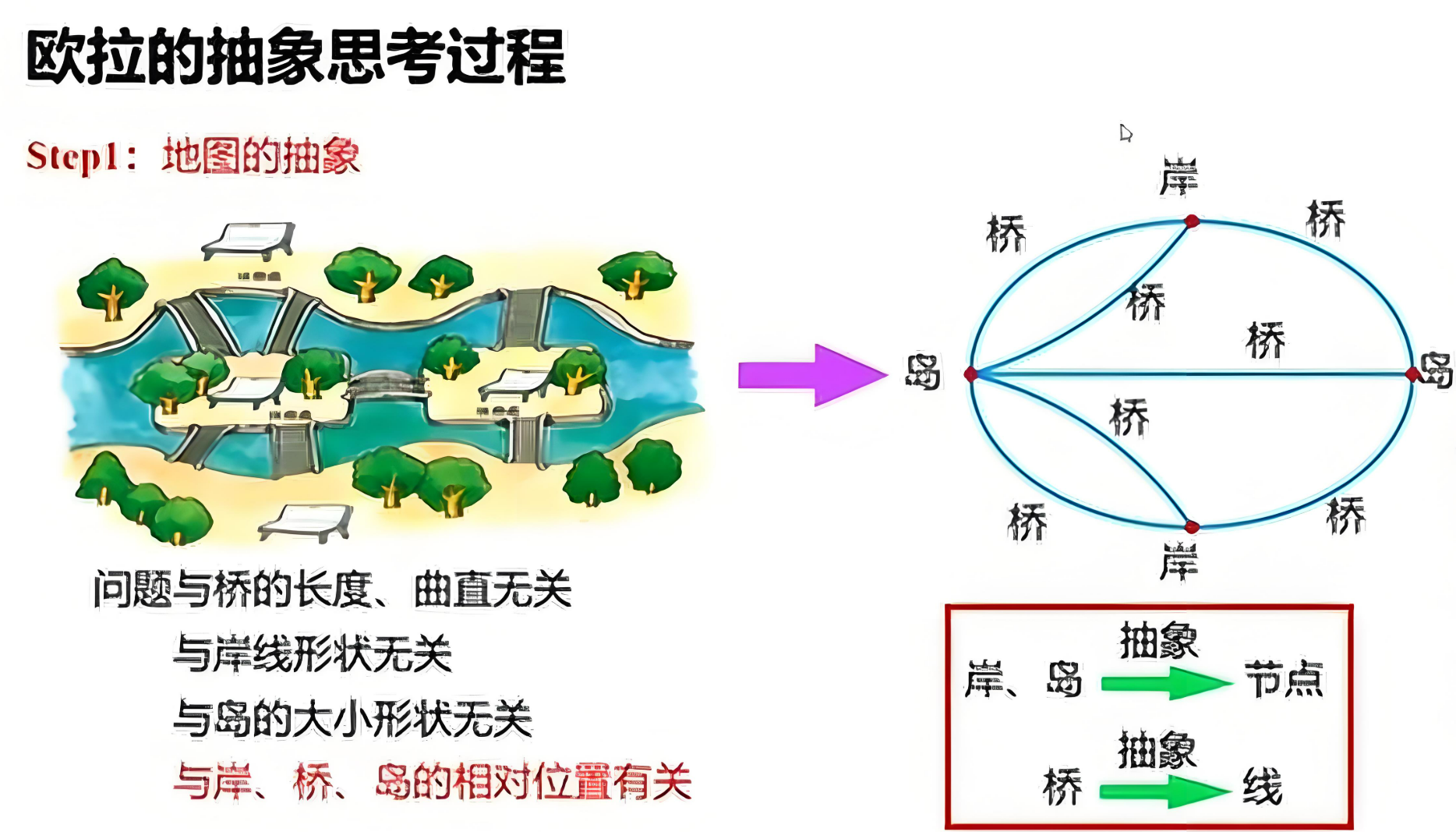
人们在日常谈话中产生了一个看似简单却耐人寻味的问题：

是否可能不重复地走过每一座桥，且只走一遍？

这个问题迅速风靡整个城市，成为当时知识分子、绅士和学生茶余饭后的智力挑战，但始终没有人能够给出确定的答案或反驳。直到这一天，一位年轻的瑞士数学家——欧拉，接到科学院的请求，希望他能给出这个问题的“数学解答”。

4.2 欧拉的突破

欧拉真正的贡献，并不仅仅是“解决”了这个问题，而是改变了解决问题的方式。他将原本“空间中的路径问题”抽象为一个纯粹的数学结构模型：图（Graph）。

  • 将四块陆地（A、B、C、D）看作四个节点（点），
  • 将七座桥看作连接这些节点的边（线）。

由此构建出我们今天熟知的“哥尼斯堡图”——历史上第一个数学意义上的图结构模型。

接着，他做出了一项前所未有的理论判断：

  • 如果一个图中有两个点的边数为奇数，则存在“欧拉通路”（一次性走完所有边）；
  • 如果图中有四个或更多奇点，则这种路径不可能存在。

哥尼斯堡图恰好有四个奇点（每块陆地都连接奇数座桥），因此欧拉断定：此路不通！

这一看似“简单”的判断，其实是一次划时代的抽象与归纳。欧拉在1736年发表了论文《论哥尼斯堡城中桥梁问题的解法》（拉丁文标题为 Solutio problematis ad geometriam situs pertinentis），这篇短短几页的文章，标志着图论的诞生，也奠定了后来的拓扑学雏形。

4.3 启示与意义

欧拉七桥问题的突破之处，在于他首次摆脱了“度量”和“几何形状”的依赖，转而关注对象之间的连接关系。这种转变在数学史中极为关键：

维度 意义说明
数学意义 创立图论，为后来的拓扑、离散数学、组合数学打下基础
思维方式 强调“结构”胜于“形状”，几何不在形，而在连接——拓扑学核心思想
方法论 提出“从问题 → 抽象建模 → 理论推导 → 结构判断”的系统化解题路径
应用前景 图论广泛用于交通优化、通信网络、社交网络分析、基因序列重构等领域

七桥问题不仅是城市趣题的解答，更是人类对“结构性思维”的第一次系统化实践。数学的伟大，不在于它解了多少难题，而在于它如何解题，以及它带来的全新思维工具。

五、欧拉公式与恒等式：数学之美的巅峰

5.1 欧拉公式：复分析的奠基之作

欧拉公式是数学史上的璀璨明珠，其内容为：

\[e^{ix} = \cos x + i\sin x \]

其中，\(x\) 为实数，\(i\) 是虚数单位，\(e\) 是自然对数的底。这个公式首次揭示了指数函数与三角函数之间的深层联系，标志着复变函数理论的诞生。
从分析学的角度看，\(e^{ix}\) 可以通过幂级数展开方式定义，而 \(\cos x\) 和 \(\sin x\) 也分别具有相似的幂级数展开形式。欧拉通过代入虚数 \(ix\)，实现了这三种函数的统一。这种统一性不仅在数学分析中具有理论价值，也在电路分析、量子力学、信号处理等领域具有重要应用意义。
在几何意义上，欧拉公式说明了复平面上的单位圆可以用指数函数来表示，\(e^{ix}\) 对应于复平面上以原点为中心、模为 1、辐角为 \(x\) 的点。它为“旋转”这一概念提供了优雅的表达方式，被誉为复平面上的罗塞塔石碑。

5.2 欧拉恒等式：美的极致表达

当 \(x = \pi\)，欧拉公式转化为：

\[e^{i\pi} + 1 = 0 \]

这就是著名的欧拉恒等式（Euler’s Identity）。

它被称为数学中最美的公式之一，因为它将五个最基本的数学常数——

  • \(e\)：自然对数的底，分析学的核心；
  • \(i\)：虚数单位，复数的基础；
  • \(\pi\)：圆周率，几何的灵魂；
  • \(1\)：乘法恒等元；
  • \(0\)：加法恒等元；

这五个看似毫不相关的常数，竟然通过一个极其简洁优雅的公式完美结合在一起。
欧拉恒等式不仅是一种数学的联通性奇迹，也象征着宇宙深层结构中的某种和谐。在美学、哲学甚至宗教思考中，它都常被引用为“数学之美的巅峰”。

这一公式也因此成为数学界美学与逻辑完美统一的象征，被视为欧拉对人类文明的最大馈赠之一。

六、拓扑与结构思维的播种者

欧拉在数学史上的一项深远贡献，是他将传统几何学中对“度量”（如长度、角度）的关注，转移到了对结构、关系和连通性的思考。这种转变的起点之一，便是著名的柯尼斯堡七桥问题。面对一个看似与几何无关的城市交通问题，欧拉用“点”和“边”的概念，构造出图论的雏形。他首次抽象出“桥”为边、“陆地”为点，由此确立了判断是否能一次走完所有桥的欧拉通路思想。此后，“欧拉图”成为图论的基石。

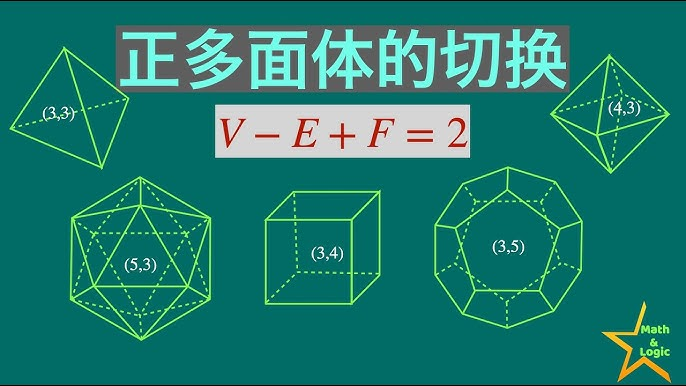
更具哲学意味的，是他在1758年提出的欧拉多面体公式：

\[V - E + F = 2 \]

其中 \(V\)、\(E\)、\(F\) 分别表示凸多面体的顶点数、棱数和面数。这一恒等式揭示了一个深层的拓扑结构特性，为19世纪拓扑学的建立（如庞加莱对“欧拉示性数”的推广）奠定基础。
欧拉的“点-边-面”抽象，已成为现代科学的共通语言。无论是社交网络、神经网络中的图神经结构，还是分子建模与生物网络分析，欧拉的结构思维正在人工智能、数据科学与复杂系统建模中持续发挥影响。

七、后世影响：从拉格朗日到神经网络

欧拉的数学思想并未止步于18世纪，而是深深影响了此后几个世纪的科学发展。他不仅留下大量原始公式、定理和方法，更重要的是，他引领了一种全新的结构化数学思维模式。这一思想内核，被后世众多大师继承、发展，演化为今日多个核心学科的基础：

继承者 传承与发展成果
拉格朗日 在欧拉力学基础上发展变分法，建立拉格朗日力学体系，成为经典力学支柱之一
傅里叶 继承欧拉的三角级数思想，发展为傅里叶级数和傅里叶分析，开创信号处理先河
高斯 在数论中拓展欧拉的乘积公式，建立模理论与二次互反律，深化解析数论体系
库尔特·雷维 受到欧拉多面体公式启发，开创现代拓扑学，强调不变量与空间结构之间的关系
现代人工智能 **图神经网络（GNN）**架构建立在欧拉的图论思维之上，应用于社交、推荐、知识图谱等领域

欧拉留下的不仅是理论基础，更是工具与语言。他的众多公式与方法至今仍活跃在科学研究与工程实践中：

  • 欧拉法：求解微分方程的经典数值方法，适用于数值模拟与工程仿真；
  • 欧拉–伯努利梁理论：结构工程中分析材料弯曲、应力的重要模型；
  • 欧拉图与欧拉路径：在电路设计、路径优化中广泛应用；
  • 图模型：用于生物信息学中的蛋白质对接、基因关系建模等；
  • 网络拓扑结构分析：成为计算机科学与通信网络架构的基础框架。

可以说，欧拉的思想从纯数学延展至应用数学，再渗透进现代科技的底层架构。他不仅属于18世纪，更属于今天的人工智能与信息网络时代。他的思维，早已超越了时代，仍在无声地指引着科学的前路。

八、欧拉其人：理性、信仰与情感

莱昂哈德·欧拉不仅是数学史上无可争议的巨人，更是一位深具人格魅力的温厚学者。他的一生不仅奉献给科学，更体现出强烈的理性精神与虔诚信仰的和谐统一。欧拉的人格面貌和他辉煌的学术成就同样令人敬仰。

欧拉在晚年几乎完全失明，视力的丧失并未削弱他的创造力和工作热情。他凭借惊人的记忆力和坚韧的意志，通过口述完成了大量论文与著作。据统计，失明后他仍保持每天完成一篇论文的高产状态，这种毅力和专注令人叹为观止。欧拉的这种勤奋体现了他对数学无尽热爱的精神内核。
作为一个虔诚的基督徒，欧拉认为科学和信仰并不冲突，而是可以相辅相成的。他曾多次用数学的严谨思维来解释圣经的深奥含义，试图为宗教信仰搭建理性与感性的桥梁。欧拉的这一尝试不仅显示了他的思想宽容，也为后世科学家树立了理性与信仰和谐共存的榜样。
在教育理念上，欧拉同样体现出开明与进步。他积极参与女性教育，编写了适合女学生的数学教材，反对将科学教育作为男性特权。他相信科学知识应该普及到所有人，反对因性别或社会地位限制学习的观点，这在当时是非常先进的思想。
欧拉一生低调谦逊，不喜争权夺利，也极少与人发生激烈争论。他更喜欢潜心钻研，在数学的浩瀚海洋中自由徜徉。他的同事和学生都称他为和蔼可亲、乐于助人的导师，这种人格魅力为他赢得了广泛尊敬。

欧拉不仅是理性与智慧的化身，更是虔诚与谦逊的典范。他用数学书写辉煌，也用人格传递光辉，成为科学与人文完美融合的典范。

九、结语：数学世界的永恒灯塔

欧拉是数学史上少有的“全才”，他的足迹几乎遍布18世纪所有重要数学与物理分支。他不仅提出数以百计的重要定理、公式与方法，更通过统一数学语言和符号，建立起沟通不同领域的桥梁。而在哥尼斯堡七桥问题中，他率先将现实结构抽象成图，开创了图论和拓扑学的先河，从此“连接性”成为数学研究的新方向。他用严谨、系统而富有创造力的方式，推动数学从“计算”走向“结构”，从“局部”走向“整体”。今天我们所使用的函数符号、三角函数记法、复数表示等，无不渗透着他的影响。欧拉不只是数学的塑造者，更是科学思想的先导者。他用一生证明，数学不是冰冷的符号堆砌，而是通向自然本质的语言与艺术。

欧拉之后，再无欧拉。

在数学的世界中，他是铺路者、搭桥人、灯塔。他让抽象不再冰冷，让逻辑拥有节奏，让计算背后有思想。他是一位数学之王，也是一位讲故事的人。

今天我们说：

  • 想解微分方程，查“欧拉法”；
  • 想写三角函数，记得“sin, cos”；
  • 想研究图结构，必读“欧拉图”；
  • 想表达宇宙美，念出 \(e^{i\pi} + 1 = 0\)。

他活在我们每一个公式中。

参考文献

  1. Euler Archive: https://eulerarchive.maa.org/
  2. Dunham, W. Euler: The Master of Us All
  3. 吴大任. 《欧拉的数学世界》. 高教出版社
  4. Boyer, C.B. 《数学发展简史》
  5. Wikipedia - Leonhard Euler
  6. CNKI 数学史资源库

“在欧拉的世界中，每一个公式都是一首诗，每一个图形都是一扇窗。他不是在解题，而是在揭示宇宙的秩序。”
—— 数学家恩斯特·贝尔（Ernst Bell）

posted @ 2025-07-26 06:48  郝hai  阅读(585)  评论(0)    收藏  举报