博弈论：约翰·纳什的美丽心灵

20世纪的科学舞台上，博弈论悄然登场，从经济学的边缘工具跃升为解决社会互动、战略选择与理性冲突的核心理论。而在这场变革的中心，站着一位被誉为“理性建模的缔造者”的人物——约翰·福布斯·纳什（John Forbes Nash）。他以仅用28页的博士论文，揭示了一个改变经济学与数学世界的概念——纳什均衡。该理论深刻解答了一个看似简单却本质复杂的问题：当多个理性个体相互博弈时，如何预测他们的策略选择？他的理论被广泛应用于商战、国际政治、网络对抗、生态演化等各类领域，并成为现代博弈论的基石。

“我不相信上帝扔骰子。博弈论也不是关于赌博，而是关于理性的较量。纳什的均衡，不只是一个数学点，它是人类在复杂社会中学会共存的标志。”
—— 经济学家 罗杰·迈尔森（Roger Myerson）

目录

📌 导语：从一位数学家说起

约翰·纳什，这位20世纪最具传奇色彩的数学家之一，他的名字如今已不仅仅属于数学的范畴，更深入地影响了经济学、政治学、社会科学，甚至人工智能的发展。他在年仅21岁时发表的一篇短文，提出了“纳什均衡”的概念，这一理论为非合作博弈提供了普遍均衡解的存在性证明，彻底改写了人们对“理性”与“战略”的理解。
从冷战时期的核军备竞赛，到现代的互联网平台算法定价、市场竞争、气候协议谈判，乃至人工智能之间的多智能体协同控制，纳什均衡都作为一套基本分析框架，揭示了个体在他人行为既定下做出最优选择的本质逻辑。这不仅是一种数学工具，更是一种解释社会互动中“稳定性”与“均衡点”的方法。
纳什的思想告诉我们：即便在缺乏沟通、目标冲突的环境中，个体行为之间依旧存在某种可预期、可分析的秩序。这种理性行为模式的稳定状态，正是博弈论试图捕捉的核心。而纳什均衡，正是理解这种秩序的钥匙。

一、传奇人生：约翰·纳什的轨迹

1.1 童年与教育：天才的觉醒

1928年，约翰·纳什出生于美国西弗吉尼亚州的一个普通家庭。幼年时期的他性格内向、寡言少语，却展现出惊人的逻辑思维能力。他痴迷于数字和谜题，常以自学方式超前掌握数学知识。17岁，他进入卡耐基理工学院（今卡耐基梅隆大学）主修化工，但很快意识到自己对数学的热爱远远超过工程。导师们注意到他在抽象思维上的天赋，并鼓励他转向纯数学方向。
不久后，纳什获得普林斯顿大学的全额奖学金。在申请材料中，数学家理查德·杜宾（Richard Duffin）只写下了简短的一句话：“This man is a genius.” 这封推荐信堪称史上最有力的“简历”。
年仅21岁，纳什完成了只有27页的博士论文《非合作博弈》。他首次提出并证明了“纳什均衡”的存在性，这一理论为博弈论开辟了新的天地。尽管这篇论文在当时并未引起广泛注意，却在后来的几十年中成为经济学、政治学乃至人工智能等多个学科的基石。

1.2 病魔与光辉：美丽心灵的低谷

然而，纳什的人生并非一帆风顺。在事业初期快速崛起后，他在30岁前后突然患上了精神分裂症，产生妄想、幻觉和严重的认知障碍。这场疾病几乎摧毁了他的正常生活与学术生涯，他被迫离开研究岗位，甚至在长期内成为普林斯顿校园中“沉默徘徊的幽灵”。
尽管如此，纳什的理性与精神顽强地存活着。他的妻子艾丽西亚始终陪伴左右，成为他复归之路的支柱。20世纪80年代后期，纳什逐渐恢复了认知能力，并在1990年代重新被学术界接纳。
1994年，纳什与约翰·海萨尼、赖因哈德·泽尔滕共同获得诺贝尔经济学奖，以表彰他们在博弈论中的开创性贡献。2015年，他又因非线性偏微分方程研究获颁数学界最高荣誉“阿贝尔奖”。然而不久之后，他与妻子在一场车祸中不幸去世，结束了这段跌宕起伏、充满光辉与痛苦交织的传奇人生。

二、纳什革命：非合作博弈的出现

2.1 博弈论的起点：冯·诺伊曼与摩根斯特恩

在博弈论成为独立学科之前，它仅仅是数学与经济交叉地带的一种分析方式。直到 1944 年，冯·诺伊曼与经济学家摩根斯特恩合著的《博弈论与经济行为》（Theory of Games and Economic Behavior）才标志着博弈论的正式诞生。该书提出合作博弈模型，以“最大最小策略”为核心，主要研究两个以上参与者在可以签订约束性合约的情况下如何进行分配和协作。虽然构建了一套逻辑自洽的分析框架，但它存在两大核心限制：

  • 合约依赖：分析必须假定玩家间可以缔结可信约束协议；
  • 适用范围窄：不适用于现代经济社会中大量的“匿名决策”与“信任缺失博弈”。

因此，这一理论难以解释更广泛的“竞争—冲突”结构，如市场竞争、国际政治博弈或平台经济。

2.2 纳什的关键突破

约翰·纳什的伟大之处，在于跳脱合作假设，提出了非合作环境下参与者的理性行为模式，即后人所称的“纳什均衡（Nash Equilibrium）”。
纳什的核心洞察是：在无需强约束、不可签订合约的情境中，只要每位博弈参与者都做出了最优回应（best response），那么这种策略组合就是一种自洽的稳定状态。其含义是：

一旦各方达到该均衡点，任何一方单独偏离都不会带来更好的结果。

这在理论上完成了从“理想契约合作”到“现实竞争应对”的飞跃，极大拓展了博弈论的应用边界。与同时代顶级科学家相比，纳什将抽象思维引入社会互动逻辑，是一次范式转变。以下用表格方式对比三位代表人物：

学者 核心贡献 方法特征 对博弈论的影响
冯·诺伊曼 创立零和博弈、提出最大最小原理 数学严格、线性代数方法 奠定合作博弈理论基础
库尔特·戈德尔 不完全性定理、逻辑系统的极限探讨 元数学、形式逻辑推演 启发纳什思考系统内部一致性
约翰·纳什 提出非合作博弈与纳什均衡理论 稳定性分析、反应函数法 重塑博弈论内核，使之具备普适应用能力

从上表可以看出，冯·诺伊曼建立的是博弈论的数学大厦，而纳什在其中注入了社会行为的“内在逻辑”。特别是他提出的均衡不仅适用于“经济人假设”，也广泛适用于生态系统、政治制度设计、甚至人工智能中的强化学习模型。

2.3 纳什均衡的三重意义

  • 理论意义：为非合作博弈提供了数学解的存在性证明，使博弈论模型具有完整性与普适性。
  • 应用意义：被广泛应用于价格竞争、竞标拍卖、政治联盟、网络流量控制等现实问题中。
  • 哲学意义：提出了一种“稳定性”范式，即个体理性如何自发形成系统性秩序，为理性选择理论奠定基础。

纳什的贡献不仅解决了冯·诺伊曼模型的缺陷，更预示着一种思考世界的新方式。正如数学家 Hal Varian 所言：

“纳什均衡是一种社会现象的抽象公式，它解释了为何看似混乱的互动背后可能隐藏着一种稳定秩序。”

三、理论核心：纳什均衡的精义

3.1 均衡定义与数学结构

在博弈论中，一个博弈 $ G $ 通常由以下三要素构成：

  • 参与者（Players）：理性决策者集合，记为 $ N = {1, 2, \dots, n} $；
  • 策略空间（Strategy Sets）：每个参与者可选择的策略集合，记为 $ S_i $；
  • 效用函数（Payoff Functions）：每个参与者的效用或收益函数，表示为 $ u_i : S_1 \times S_2 \times \cdots \times S_n \to \mathbb{R} $，反映策略组合下的偏好程度。

纳什均衡的纯策略定义是：
一个策略组合 $ s^* = (s_1^, s_2^, \dots, s_n^*) \in S_1 \times S_2 \times \cdots \times S_n $，满足对于所有玩家 $ i $ 和其所有可能的替代策略 $ s_i \in S_i $，均有

\[u_i(s_i^*, s_{-i}^*) \geq u_i(s_i, s_{-i}^*) \]

其中，$ s_{-i}^* $ 表示除玩家 $ i $ 以外其他玩家的策略组合。换言之，在其他玩家策略不变的情况下，没有玩家能通过改变自己的策略获得更高的收益。

然而，现实中并非所有博弈都有纯策略纳什均衡。为此，纳什引入了混合策略——即玩家以一定概率分布选择策略。基于这一点，他借助拓扑学中的Kakutani不动点定理，证明了每个有限博弈至少存在一个混合策略纳什均衡。这一存在性证明极大丰富了博弈论的理论基础，使其具备数学严谨性和普适性。

3.2 经典博弈案例演绎

囚徒困境

两个嫌疑犯被捕，若均保持沉默则各判轻罪（奖励较高）；若一人背叛一人沉默，背叛者无罪，沉默者重判；若均背叛，则判中等罪。

沉默 背叛
沉默 (-1, -1) (-10, 0)
背叛 (0, -10) (-5, -5)

唯一纳什均衡是（背叛，背叛），尽管非最优，但因单方无利可图偏离，策略稳定。

猎鹿博弈

两人合作猎杀一只鹿，合作成功分享猎物；一方独自猎杀则只能捕获兔子，收益较低。合作为最优，但缺乏信任，导致均衡可能是非合作。

石头剪刀布

经典循环策略博弈，无纯策略纳什均衡，唯一混合策略均衡是三策略均等概率选择（1/3，1/3，1/3），保证长期无被预测。

Cournot二寡头模型

两家企业同时决定产量，市场价格由总产量决定。通过反应函数交叉点，找到均衡产量，反映企业在竞争环境中策略的稳定点。

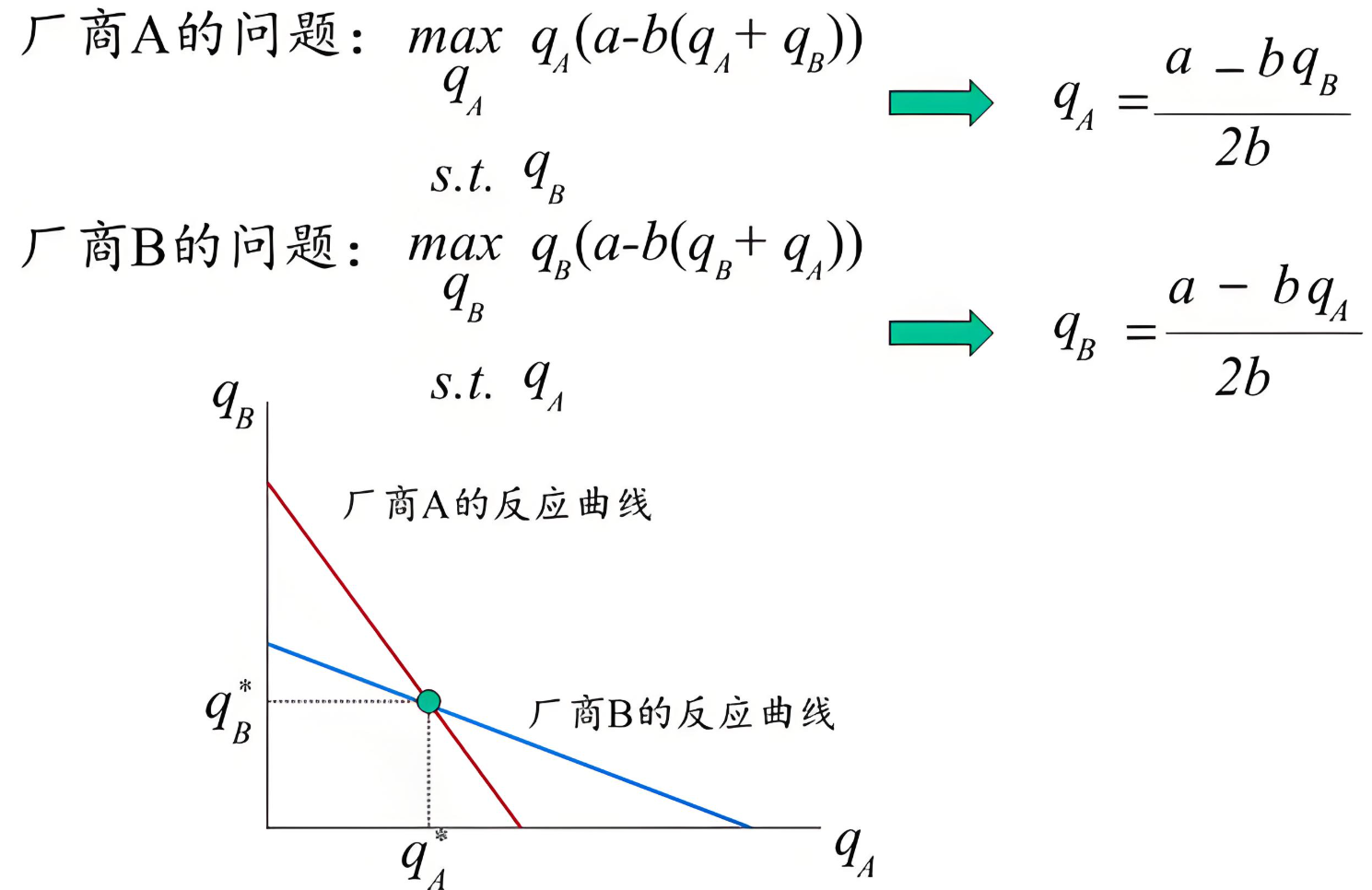
纳什均衡的“稳定”与“非最优”特性

纳什均衡的核心是“稳定性”：没有玩家愿意单方面偏离。但这并不保证整体效用最大化。囚徒困境即体现了这一悖论：个体理性导致集体非理性结果。纳什均衡不仅为博弈论提供了理论基石，也为理解现实中的战略互动提供了有效工具。通过纯策略和混合策略的统一框架，它揭示了理性决策者在复杂互动中的稳定行为模式。

四、纳什均衡的类型与推导方法

4.1 静态博弈 vs 动态博弈

  • 静态博弈指所有参与者同时或在不知其他人策略的情况下选择策略。典型特征是参与者策略一次性决定，均衡点通过解方程组或最优响应函数找到。
  • 动态博弈则考虑参与者按顺序选择策略，每个阶段的选择可能依赖于之前的行为，信息逐步揭示。分析方法多用逆向归纳法（Backward Induction），通过从最后阶段向前推断最优策略。
  • 博弈树（Game Tree）是动态博弈的重要表现形式，描述各节点的决策和可能结果。
  • 例如，Stackelberg模型描述领导者-跟随者的产量选择博弈，领导者先决策，跟随者观测后响应，纳什均衡通过逆推归纳确定。

4.2 完全信息博弈 vs 不完全信息博弈

  • 完全信息博弈指所有参与者知道博弈结构、策略集及其他玩家的效用函数，参与者之间信息对称。
  • 不完全信息博弈则信息不对称，玩家对其他玩家的类型、偏好或策略存在不确定性。为解决该类博弈，哈萨尼（Harsanyi）提出类型空间（Type Space）模型，用概率分布描述对方可能的类型。
  • 贝叶斯纳什均衡（Bayesian Nash Equilibrium）是对不完全信息博弈的均衡推广，要求策略在给定信念和其他参与者策略时均为最优反应。
  • 贝叶斯均衡广泛应用于拍卖设计、投标竞标、信号传递博弈等实际场景，帮助解释信息不对称下的策略选择。

4.3 重复博弈与“合作的可能性”

  • 重复博弈指相同博弈在多个时期重复进行，参与者可以基于历史行为调整策略。
  • 在无限期重复博弈中，合作成为可能，这通过Folk Theorem（民谣定理）体现：只要参与者足够耐心，几乎所有可行且个体理性约束满足的结果都可作为均衡实现。
  • 经典合作策略如“以牙还牙”（Tit-for-Tat）：参与者初期合作，若对方背叛则回以背叛，促进长期合作。
  • 这拓展了纳什均衡的稳定性概念，使得博弈不仅限于单阶段策略均衡，也涵盖动态调整与惩罚激励机制。

纳什均衡类型多样，涵盖静态与动态、完全与不完全信息，以及单次与重复博弈。不同情境下均衡的定义与推导方法各异，丰富了博弈论的应用深度与广度。

五、均衡之外：纳什思想的影响与争议

5.1 均衡的现实启示

纳什均衡为理解理性人在复杂战略环境中的行为提供了强有力的工具。基于理性人假设和信息完备的前提，纳什均衡描绘出参与者之间策略稳定的“平衡状态”，为经济学、政治学、社会学等多个领域构建了理论模型基础。它帮助决策者预测竞争对手或合作伙伴的行为，为市场竞价、国际谈判、环境治理等实际问题提供策略参考。

5.2 纳什均衡的局限与批评

尽管纳什均衡理论成就卓著，但其局限性同样明显。首先，许多博弈存在多重纳什均衡，如何从中选择合理均衡成为难题，这催生了均衡精炼理论的发展。其次，现实世界中信息往往不完全或不对称，纳什均衡的理想假设难以完全满足。更为关键的是，实际决策者常常表现出有限理性、情绪波动、社会偏好等非理性因素，纳什模型难以解释这些行为，推动了行为博弈论的兴起。

5.3 精炼路径与博弈拓展

为克服多重均衡问题，经济学家如Selten提出了子博弈完美均衡，通过对子博弈的均衡进行逐层筛选，剔除不合理均衡，使模型更具解释力。此外，演化稳定策略（ESS）引入动态视角，强调策略在群体演化中的稳定性，为生物学和社会科学提供了新的分析框架。

纳什均衡也成为机制设计理论的基石，机制设计从“设计规则”出发，确保在纳什均衡下实现期望目标，两者相辅相成，推动了拍卖理论、市场设计等领域的突破。纳什均衡既是博弈论的核心，也是理论和现实的桥梁。其影响深远但并非万能，围绕均衡的批评与改进不断推动博弈论的丰富与发展。

六、跨学科影响：纳什均衡的广泛应用

6.1 经济与政策领域

纳什均衡为现代经济学提供了坚实的理论基础，特别是在拍卖理论中发挥了重要作用。Vickrey拍卖（第二价格密封拍卖）和美国联邦通信委员会（FCC）频谱竞拍中，纳什均衡帮助设计出激励兼容的竞标机制，确保参与者在真实出价时实现策略稳定。此外，纳什均衡在平台经济定价与寡头竞争模型中，用于分析企业如何在竞争与合作之间寻找均衡策略，从而优化利润和市场份额。

6.2 社会科学与政治博弈

在国际关系领域，纳什均衡被用来解释国家间在安全、贸易、环境协议等方面的战略互动。它揭示了诸如核威慑、联盟形成等复杂博弈中策略的稳定性。选举中的多方联盟策略和政策制定过程也普遍应用纳什均衡分析，帮助政治学家理解权力分配和策略投票行为，为政策优化和选举策略设计提供理论支撑。

6.3 人工智能与多智能体博弈

随着人工智能的发展，纳什均衡在多智能体系统中扮演关键角色。强化学习算法如Q-learning和Nash-Q利用均衡概念逼近复杂环境中的最优策略组合。在自动驾驶车辆的协调决策中，纳什均衡帮助实现安全且高效的交通流控制。此外，像AlphaGo这样的AI博弈机器人，其内部策略设计和对手预测均基于博弈论原理，确保在复杂对抗中实现稳定优势。

纳什均衡作为理性行为的数学刻画，已经超越理论范畴，成为经济学、政治学及人工智能等多个领域不可或缺的分析工具，推动了学科交叉融合和技术创新。

七、数学之外：美丽心灵的启示

约翰·纳什的故事不仅是数学与经济学的传奇，更是一段关于人性、坚韧与希望的动人篇章。他以天才般的智慧开创了博弈论的新纪元，但人生的道路并非一路坦途。纳什在事业巅峰时遭遇精神分裂症的严重困扰，现实与幻觉交织，理性一度崩溃。他被迫离开学术舞台，生活陷入黑暗。
然而，这位“美丽心灵”的主人公没有被命运击倒。通过自身的努力和妻子的陪伴，纳什逐渐恢复理智，重新获得学术界的认可。他的复出不仅是个人的胜利，也象征着理性力量的坚韧与复兴。这段人生经历让人们看到，理性并非与生俱来，而是在挫折中磨砺和成长的品质。
纳什均衡的意义超越了纯粹的数学定义。它象征着即便在竞争与冲突的复杂社会环境中，人类行为依然可以通过理性加以理解和预测。这种信念为社会科学注入了希望：尽管人类不完美，理性选择和稳定均衡依旧是可追求的目标。
正如纳什本人所言：“理性让我们看到世界的秩序与和谐，哪怕现实充满了不确定和挑战。”他的故事激励着无数学者和普通人，在面对困境时保持对理性的信仰与追求。

纳什不仅用数学改变了科学，更用人生诠释了理性的力量。他的“美丽心灵”启示我们，在科学与生活的博弈中，坚持理性与信念，终将迎来属于自己的均衡与光明。

📚 延伸阅读与参考资料

为了更深入理解约翰·纳什及其对博弈论的贡献，以下文献与资料值得推荐：

  • 冯·诺伊曼 & 摩根斯特恩，《博弈论与经济行为》（Theory of Games and Economic Behavior），1944年：博弈论奠基之作，首次系统提出零和博弈与策略空间概念。
  • John F. Nash，《Equilibrium Points in N-Person Games》，Proceedings of the National Academy of Sciences, 1950：纳什均衡理论的开创性论文，仅两页却影响深远。
  • Osborne, M. & Rubinstein, A.，《博弈论导论》（A Course in Game Theory），MIT Press，1994：现代博弈论入门与中高级学习的权威教材。
  • Harold W. Kuhn（编），《The Essential John Nash》，Princeton University Press, 2002：收录纳什主要论文与生平资料，含多篇原始手稿及回顾性文章。
  • Sylvia Nasar，《A Beautiful Mind》：传记文学作品，真实还原纳什的传奇人生，2001年被改编为奥斯卡获奖电影《美丽心灵》。

posted @ 2025-07-26 06:29  郝hai  阅读(168)  评论(0)    收藏  举报