供应链选址篇:战略落点的“第一锚”
在供应链管理中,选址往往是被低估却最具战略意义的一步。无论是建设仓库、工厂,还是设立配送中心,地点的选择都深刻影响着企业的物流成本、服务效率与市场响应速度。一次恰当的选址可以构建强大的供应网络基础,而错误的选址则可能让企业在成本与效率之间长期挣扎。随着全球化、城市化和个性化需求的不断演变,供应链选址不再仅是地理位置的比选,更是一项融合数据分析、政策考量与智能优化的系统性工程。
选址是一场没有硝烟的战争,一旦落子,牵一发动全身。它是供应链布局的起点,是成本、服务、竞争力的根基。选址正确,事半功倍;选址失误,代价高昂。本文将从选址的重要性、主流方法、典型案例等方面进行系统阐述,并以亚马逊全球仓储网络为例,剖析其背后的选址逻辑与实践智慧。
一、选址为什么如此关键?
1.1 选址是供应链的原点决策
在整个供应链体系中,选址决策通常发生在系统设计的最前端。无论是新建一个仓库、制造基地,还是设立区域配送中心,其地理位置的选择不仅影响局部节点的效率,更会对整个网络的资源配置和协同能力产生连锁效应。一个优选的地点能够显著优化运输路径、缩短响应时间、降低整体运营成本,并提升服务客户的广度与深度。
具体而言,选址决定了以下几个关键方面:
- 物流效率与配送成本:位置越接近客户集聚区或交通枢纽,运输距离越短,配送时效越高,物流成本越低。
- 客户服务半径与响应速度:合理布局能够在客户周边建立快速响应机制,实现“当日达”“次日达”等高时效目标。
- 库存周转与供应稳定性:靠近供应商或上游工厂可加快物料流动,减少在途时间和安全库存占用。
- 供应商协同与原料获取:与产业集群协同布局可以形成“共生共建”的资源共享优势。
- 税收政策、土地成本与劳动力可得性:不同区域在用地政策、租金水平和劳动力结构方面差异显著,直接影响固定成本和运营弹性。
1.2 错误选址的代价极高
选址一旦确定,便具有高度的“路径依赖性”,后续的运营模式、组织结构乃至客户关系都围绕该位置展开。因此,选址错误带来的影响往往是结构性、系统性的。一项供应链研究显示,因选址失误导致的运营成本上升幅度可高达30%-50%,企业往往需要数年时间和大量资源才能缓解或纠正。
具体的代价包括:
- 高昂的迁移成本:设备搬迁、人员重组、重新装修等直接支出。
- 原有投资的沉没损失:包括土地使用权、固定资产投入、初期宣传与建设成本。
- 客户服务的短期波动:搬迁过程中可能导致交付延误、订单取消,客户满意度下降。
- 内部资源的重新配置:系统设置、人力安排、供应商合同都需调整,带来管理复杂性和协同成本上升。
因此,从战略的角度看,选址不是一次性的静态决策,而是涉及长期运营绩效和企业可持续竞争力的动态系统工程。只有基于科学方法、前瞻眼光和系统思维,才能做出真正高质量的选址决策。
二、供应链选址的核心目标与挑战
2.1 核心目标
供应链选址不仅是一个空间上的决策问题,更是企业战略、运营、成本控制与服务能力协同的综合考量。一个理想的选址方案,应在以下几个关键目标之间实现平衡:
| 目标维度 | 说明 |
|---|---|
| 成本最小 | 指在满足需求的前提下,使总成本最小化。主要包括运输成本、仓储运营成本、建设费用、人工薪资、土地租金和税费等。选址靠近高消费区虽然配送便捷,但也可能意味着更高的人力和土地成本,需权衡利弊。 |
| 响应最优 | 指企业能够以最快的速度满足客户需求,实现服务承诺。选址决定了响应时间、服务半径、库存分布等,直接关系到客户满意度和订单履约能力。 |
| 风险可控 | 包括地缘政治风险、自然灾害风险、供应中断风险等。例如,洪水高发区或地震带区域可能带来运营中断的可能性,需在初期进行充分评估。 |
| 弹性布局 | 一个优秀的供应链布局应具有前瞻性和灵活性,能够适应未来业务的扩张、收缩、市场变化等,避免“锁死式投资”。弹性选址通常意味着可以通过模块化建设、租赁选项或可拓展设施实现动态调整。 |
2.2 常见挑战
在实际操作中,实现上述目标并不容易,企业往往会遇到多方面的困难与挑战:
- 多目标冲突:供应链选址是一个多目标优化问题,经常面临“成本最小化”与“服务最优化”的冲突。例如,若仅追求低成本,可能会远离客户群体,导致响应延迟;反之,如果极度贴近客户,则建设和运营成本大幅上升。因此,如何平衡这两者,是核心挑战之一。
- 数据不确定性:选址需要基于对未来市场需求、运输费率、土地成本、政策走向等变量的预测,但这些数据往往存在不确定性和波动性。尤其是在宏观经济环境剧烈变化或地缘政治影响加剧的背景下,过去的数据可能并不能准确反映未来趋势。
- 约束条件复杂:实际选址不仅仅是技术优化问题,还需满足多种外部与内部约束。例如,土地使用审批程序繁复,环保法规限制施工进度,当地政府的招商政策也可能出现临时调整,甚至还涉及居民关系协调、上下游企业配套等非技术性条件。
- 技术与计算要求高:随着供应链网络越来越复杂,选址问题演变为典型的 NP-hard 组合优化问题。在考虑多仓库、多客户、多商品、多时间周期的综合情境下,模型求解的计算复杂性急剧上升。为此,往往需要借助专业的运筹优化算法、地理信息系统(GIS)与启发式方法(如模拟退火、遗传算法等)来辅助决策。
供应链选址不是简单的点选过程,而是战略性、系统性、技术性的重大工程,要求企业在不确定的未来中做出“最优中的稳妥”选择。
三、供应链选址的主流方法体系
在现实应用中,供应链选址既是一项依赖战略眼光的宏观布局任务,也是一项依托模型求解的技术问题。因此,选址方法大致可以分为定性方法与定量方法两大类,二者并非对立,而是相辅相成,往往组合使用。
3.1 定性方法:战略与经验导向
定性方法强调管理者的战略判断与经验积累,适用于信息不完全或指标难以量化的情境。常用方法包括:
| 方法 | 核心特点 | 适用场景 |
|---|---|---|
| SWOT分析 | 从优势、劣势、机会、威胁四个维度综合分析内外部环境 | 战略级选址、宏观区域初筛 |
| 打分法 | 依据多个维度(如交通、租金、劳动力)设权重并评分 | 候选点优劣排序、定性快速评估 |
| 专家评估法 | 借助领域专家的主观判断与经验进行判断 | 样本小、定量信息缺乏时的辅助决策 |
定性方法具有灵活、简便、低成本等优势,但也存在主观性强、难以复现、易受偏见影响等局限性。
3.2 定量方法:模型与数据驱动
定量方法则侧重构建数学模型,基于数据求解最优方案,适合结构明确、变量可量化的问题,常见模型包括:
(1)重心法(Gravity Model)
- 假设运输成本与客户之间的距离成正比。
- 利用需求点的权重与地理坐标求加权平均位置,得到“物流中心点”。
- 常用于初步仓库或配送中心选址。
公式如下:
(2)0-1整数规划模型
- 用决策变量 \(x_{j} \in \{ 0 , 1 \}\) 表示是否在位置 \(j\) 建站。
- 目标通常是最小化建设成本+运输成本之和,约束包括客户需求、站点容量、服务范围等。
- 常用于网络整体规划,尤其是工厂-仓库-客户三层结构中。
(3)覆盖模型(Covering Models)
- 最大覆盖模型:在给定预算下,选出有限个站点,最大程度覆盖客户。
- 最小覆盖模型:在覆盖所有客户的前提下,选出最少的站点数。
- 适用于应急物流、医疗救援、公共服务网络布局。
(4)模拟退火、遗传算法等启发式算法
- 面对大规模组合问题或非凸解空间,传统精确算法求解困难。
- 启发式方法可通过模拟自然选择、退火过程等机制,逼近最优解。
- 通常与GIS(地理信息系统)结合,集成多源数据(地形、交通、成本、需求分布)进行动态分析。
定性方法适合“战略方向”判断,定量方法适合“最优位置”测算。在实际项目中,两者常融合使用:先定性筛选区域,再定量建模求解,从而实现科学与经验的双轮驱动。
3.3 供应链仓库选址
问题描述
某公司拥有9家商店,现需要建造工厂为商店提供商品。已知有ABCD四种工厂类型,每种工厂最多建造一个,建造不同的工厂的成本各不相同,A需要500,B需要600,C需要700,D需要800.不同的工厂拥有不同的库存容量,A为40,B为55,C为73,D为90。对于9家商店而言,其对商品的需求量各不相同,具体如下表所示:
| 商店编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 商品需求 | 10 | 14 | 17 | 8 | 9 | 12 | 11 | 15 | 16 |
并且,不同的工厂将货物运送到不同商店的代价也不相同,如下表所示:
| 商店1 | 商店2 | 商店3 | 商店4 | 商店5 | 商店6 | 商店7 | 商店8 | 商店9 | |
|---|---|---|---|---|---|---|---|---|---|
| A | 55 | 4 | 17 | 33 | 47 | 98 | 19 | 10 | 6 |
| B | 42 | 12 | 4 | 23 | 16 | 78 | 47 | 9 | 82 |
| C | 17 | 34 | 65 | 25 | 7 | 67 | 45 | 13 | 54 |
| D | 60 | 8 | 79 | 24 | 28 | 19 | 62 | 18 | 45 |
为了简化问题,假设每家商店仅能由一家工厂供货。 请问该建造哪些工厂,以及决定这些工厂向哪些商店供货,才能使得总成本最低?
问题概述
某公司需为9家商店供应商品。公司可以建造4种类型的工厂:A、B、C、D,每种工厂最多建一个。不同工厂有不同的建造成本、产能,以及不同的运输成本到每家商店。每家商店必须由一家建成的工厂供货,目标是选择建哪些工厂、每家商店由谁供货,使得建造成本和运输成本之和最小。
符号与集合定义
- 工厂集合:\[P =\{ A , B , C , D \} \]
- 商店集合:\[S = \{ 1 , 2 , \ldots , 9 \} \]
参数定义
| 参数符号 | 含义 | 数据来源 |
|---|---|---|
| \(b_{p}\) | 建造工厂 \(p\) 的固定成本 | \(b_{A} = 500; b_{B} = 600 ; b_{C} = 700 ; b_{D} = 800\) |
| \(c_{p}\) | 工厂 \(p\) 的最大供货能力 | \(c_{A} = 40; c_{B} = 55; c_{C} = 73 ; c_{D} = 90\) |
| \(d_{s}\) | 商店 \(s\) 的商品需求量 | \(d = \left[\right. 10 , 14 , 17 , 8 , 9 , 12 , 11 , 15 , 16 \left]\right.\) |
| \(t_{p s}\) | 将商品从工厂 \(p\) 运输到商店 \(s\) 的单位运费 | 从题中表格给定 |
决策变量定义
- \(z_{p} \in \{\ 0 , 1 \}\):
若 \(z_{p} = 1\),表示工厂 \(p\) 被建造;否则 \(z_{p} = 0\)。 - \(x_{p s} \in \{ 0 , 1 \}\):
若 \(x_{p s} = 1\),表示工厂 \(p\) 向商店 \(s\) 供货;否则为 0。
数学模型
🎯 目标函数
最小化建厂成本 + 运输成本:
📌 约束条件
(1)每家商店仅由一家工厂供货:
即每家商店只能由一个工厂供应。
(2)仅当工厂建成时才能供货:
这确保如果工厂没建成(\(z_{p} = 0\)),就不能给任何商店供货。
(3)工厂供货总量不能超过其库存能力:
含义:如果工厂未建,则右边为0,不能供货;如果建成,其最大供货量不能超过自身库存。
✅ 变量类型约束
模型结构总结
| 部分 | 数学表示 | 含义 |
|---|---|---|
| 决策变量 | \(z_{p} , x_{p s}\) | 建厂与供货决策 |
| 目标函数 | \(\sum b_{p} z_{p} + \sum t_{p s} x_{p s}\) | 总成本最小 |
| 商店服务 | \(\sum_{p} x_{p s} = 1\) | 每商店仅由一厂供货 |
| 建厂才供货 | \(x_{p s} \leq z_{p}\) | 未建厂不可供货 |
| 工厂产能 | \(\sum_{s} d_{s} x_{p s} \leq c_{p} z_{p}\) | 总供货 ≤ 产能 |
| 变量类型 | \(\{ 0 , 1 \}\) | 二进制变量 |
模型python求解
import pulp
# 工厂与商店集合
factories = ['A', 'B', 'C', 'D']
stores = list(range(9))
# 参数
demand = [10, 14, 17, 8, 9, 12, 11, 15, 16]
build_cost = {'A': 500, 'B': 600, 'C': 700, 'D': 800}
capacity = {'A': 40, 'B': 55, 'C': 73, 'D': 90}
# 单位运输成本(已符合 t_ps)
trans_cost = {
'A': [55, 4, 17, 33, 47, 98, 19, 10, 6],
'B': [42, 12, 4, 23, 16, 78, 47, 9, 82],
'C': [17, 34, 65, 25, 7, 67, 45, 13, 54],
'D': [60, 8, 79, 24, 28, 19, 62, 18, 45]
}
# 模型初始化
model = pulp.LpProblem("Factory_Selection_and_Assignment", pulp.LpMinimize)
# 决策变量
z = pulp.LpVariable.dicts("z", factories, cat='Binary') # 是否建造工厂
x = pulp.LpVariable.dicts("x", [(p, s) for p in factories for s in stores], cat='Binary') # 是否由p给s供货
# 目标函数(运费项不乘以需求)
model += (
pulp.lpSum([build_cost[p] * z[p] for p in factories]) +
pulp.lpSum([trans_cost[p][s] * x[(p, s)] for p in factories for s in stores])
)
# 约束1:每个商店仅由一个工厂供货
for s in stores:
model += pulp.lpSum([x[(p, s)] for p in factories]) == 1
# 约束2:未建工厂不能供货
for p in factories:
for s in stores:
model += x[(p, s)] <= z[p]
# 约束3:工厂产能不能超过为其分配的需求
for p in factories:
model += pulp.lpSum([demand[s] * x[(p, s)] for s in stores]) <= capacity[p] * z[p]
# 求解模型
model.solve(pulp.PULP_CBC_CMD(msg=False))
# 输出结果
# 输出结果(符合你给出的样式)
print("建造的工厂:")
for p in factories:
if pulp.value(z[p]) > 0.5:
print(f" 工厂 {p} 被建造")
print("\n商店分配情况:")
for s in stores:
for p in factories:
if pulp.value(x[(p, s)]) > 0.5:
print(f" 商店 {s + 1} 由工厂 {p} 供货")
print(f"\n总成本为:{pulp.value(model.objective)}")
建造的工厂:
工厂 A 被建造
工厂 C 被建造
商店分配情况:
商店 1 由工厂 C 供货
商店 2 由工厂 A 供货
商店 3 由工厂 A 供货
商店 4 由工厂 A 供货
商店 5 由工厂 C 供货
商店 6 由工厂 C 供货
商店 7 由工厂 C 供货
商店 8 由工厂 C 供货
商店 9 由工厂 C 供货
总成本为:1457.0
四、选址因素系统解析:从宏观到微观
在工厂或配送中心选址过程中,需从战略高度出发,综合考虑宏观与微观层面的多种影响因素。宏观层面影响区域发展与战略匹配,微观层面则直接决定运营效率与成本控制。下表系统展示两大层级的主要考量内容:
4.1 宏观层面因素
| 维度 | 关键要素 | 说明 |
|---|---|---|
| 政策 | 地方政府招商政策、土地使用权、财政补贴 | 是否享有税收减免、工业用地优惠、开办企业便利程度等政策支持 |
| 法规 | 环保约束、贸易协议、关税政策 | 地区环保法严格程度、是否属于自由贸易区、进出口政策及关税壁垒情况 |
| 地理 | 地震带、水资源、气候条件 | 是否存在自然灾害风险、水源是否充足、气候是否适宜生产与存储 |
| 市场 | 接近消费市场、未来增长潜力 | 区域内市场容量、需求增长趋势及是否为企业战略布局重点区域 |
4.2 微观层面因素
| 维度 | 关键要素 | 说明 |
|---|---|---|
| 成本 | 地价、房租、人工、税负 | 地区运营成本是否具备竞争力,包括用地成本、人力资源支出和本地税率等 |
| 交通 | 高速公路、铁路、港口、机场 | 区位交通通达性如何,是否利于原材料进厂和产品配送出厂,降低物流成本 |
| 供应商 | 配套企业群是否齐全 | 是否临近主要原材料或组件供应商,可否形成集聚效应,提升供应链反应速度 |
| 劳动力 | 技术工人可得性、劳动力成本 | 当地是否有足够合格劳动力,培训成本是否可控,是否利于生产效率提升 |
| 基础设施 | 电力、水气网、网络通信等 | 生产所需资源保障是否充足、通讯设施是否完备,能否保障生产连续性及数据协同 |
五、典型案例:亚马逊的全球仓储选址策略
5.1 案例背景
亚马逊成立于1994年,经过近三十年的高速发展,已成为全球电商巨头。其仓储物流体系作为核心竞争力之一,经历了从单一仓库到全球复杂网络的演变。截至2024年,亚马逊在全球拥有超过1100个运营中心,覆盖北美、欧洲、亚洲等主要市场。这些仓库不仅承担存储功能,更通过自动化分拣、智能调度,实现高效的订单履约,支持“当日达”“次日达”甚至“小时达”的物流服务。
5.2 选址策略概览
亚马逊的选址策略具有多层级、全方位的特点,涵盖国家/区域、城市和具体场址三个层面,形成高度协同的仓储网络。
| 战略层级 | 布局目标 |
|---|---|
| 国家/区域级 | 靠近消费大市场、主要港口及贸易节点,以降低跨境及长途运输成本 |
| 城市级 | 综合考虑客户密度、交通基础设施状况、劳动力成本和政策环境,确保配送效率和成本优势 |
| 场址级 | 选取具备土地可扩展性、交通便利、配套完善的工业园区或经济开发区,以满足未来扩张需求 |
在国家层面,亚马逊优先选址在经济发达、人口密集且消费潜力巨大的地区。例如,在美国,其仓储网络重点覆盖加州、纽约、德州等主要消费市场,且靠近海港和机场,便于商品的快速进出。在城市层面,亚马逊会详细评估城市内部的交通拥堵状况、公路网络连通性,以及人力资源市场,确保仓库的选址能够最大化提高配送时效和降低运营成本。在具体场址选择上,亚马逊倾向于选择土地供应充足、具备良好基础设施的工业园区,方便后续扩建和技术升级,同时获得政府优惠政策支持。
5.3 多维度分析
交通可达性
亚马逊极度重视仓库的交通可达性,优选靠近高速公路出口、铁路中转站和主要机场的地点,以确保货物可以快速进出和转运。例如,芝加哥的仓库选址临近I-55州际公路,这不仅方便原材料供应,也保证了配送速度。此外,港口周边仓库能有效缩短进口货物到达时间,提升供应链响应速度。
服务半径与订单响应
亚马逊设计了多层次仓储结构:包括大型配送中心(Fulfillment Center)、中型分拣中心(Sortation Center)和小型城市前置仓(Delivery Station)。这种结构让订单能够在最短时间内从最近的仓库发出,实现“当日达”“次日达”目标,提升客户满意度。例如,城市内的Delivery Station可以更快响应消费者需求,减少最后一公里配送时间。
地区劳动力
亚马逊在选址时,详细分析当地的劳动力市场情况,包括失业率、工资水平、劳工法规和技术工人供给情况。合理的劳动力市场不仅保障了用工的稳定性,也有助于降低人力成本。例如,一些仓库设立在劳动力资源充足且薪酬合理的地区,同时注重劳动环境与安全,以减少人员流失和培训成本。
政策激励
亚马逊的仓储布局常伴随地方政府的积极招商引资政策支持,如税收减免、财政补贴和免费土地等。多个美国州政府通过制定专项优惠政策吸引亚马逊入驻,推动本地经济发展。这些政策不仅降低了亚马逊的建厂及运营成本,也增强了其供应链的灵活性和扩展能力。
5.4 地理信息辅助系统(GIS)的运用
亚马逊利用GIS技术,将交通流数据、人口密度热力图、自然地理障碍等信息进行空间分析,实现更加精准和科学的选址决策。GIS技术能够帮助企业识别潜在区域的优势与风险,例如避开自然灾害高发区、选择交通网络便捷区域。借助大数据和地理信息系统,亚马逊能够快速模拟不同选址方案的配送效果和成本结构,为决策提供科学依据。
5.5 案例总结:战略+算法的融合
亚马逊的选址策略体现了数据驱动和战略协同的深度融合:
- 数据与模型支撑
通过收集多源数据(包括经济指标、物流成本、人口数据等),结合运筹优化模型,实现科学定量评估。 - 分层级网络设计
从国家到城市再到具体仓库,实现网络的层次化布局,兼顾规模经济和响应速度。 - 动态迭代优化
亚马逊持续追踪选址后的运营表现,根据市场和技术变化动态调整布局,保持仓储网络的弹性和竞争力。
这种“战略引导 + 算法驱动”的选址方法,极大提升了亚马逊供应链的效率和客户体验,也成为现代企业仓储选址的典范。
六、选址与企业战略协同的路径建议
选址不仅是一个地理决策,更是战略导向下资源配置的结果。不同类型企业在不同发展阶段、不同经营战略下,对选址因素的关注点也存在显著差异。因此,选址工作应与企业战略目标深度协同,体现企业的核心能力布局与长期增长规划。
6.1 不同行业的选址侧重点
| 行业类型 | 选址重点 |
|---|---|
| 零售业 | 靠近消费终端、快速响应消费者需求、强调人流与便利性 |
| 制造业 | 靠近原材料、上下游配套供应商、注重土地、交通和劳动力成本 |
| 医药物流 | 靠近主要医疗机构,强调冷链温控设施与配送时效 |
| 电商平台 | 重点覆盖高密度城市群,要求高频次快速分拨与库存调度能力 |
每个行业在选址时都应根据其“价值创造链”中最关键的环节来制定权重侧重。例如,电商需快速履约服务,因此更倾向于选择靠近城市消费中心的仓配中心;制造业则更倾向原材料集聚区以降低采购成本。
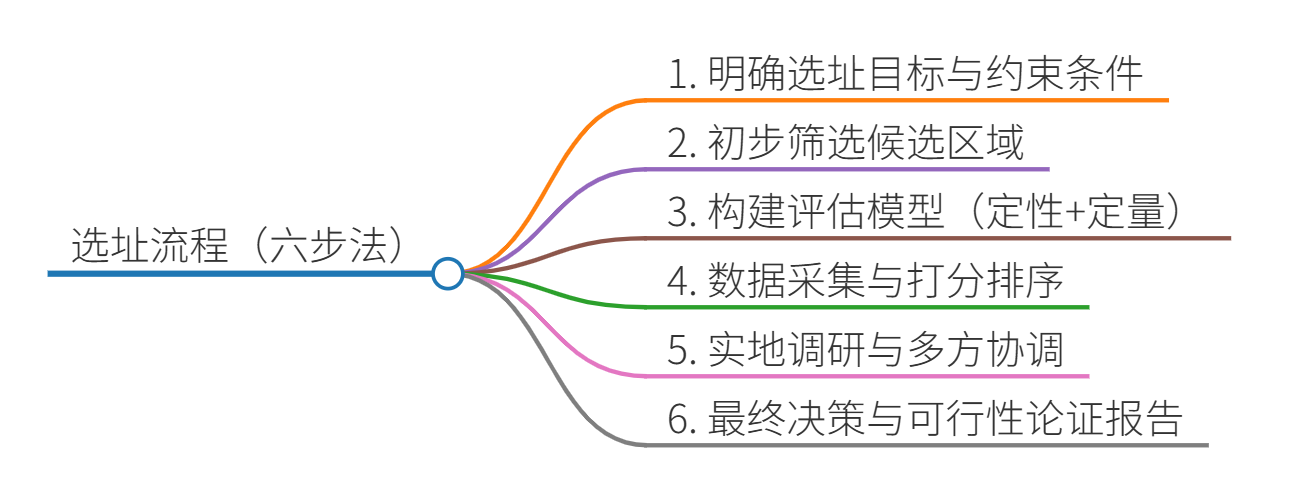
6.2 选址流程建议(六步法)
企业可参考以下“选址六步法”,在系统分析与实证调研的基础上,构建可操作的选址决策路径:
- 明确选址目标与约束条件
明确企业当前战略定位,如成本领先、市场扩张或响应速度优化,并识别基本约束如预算、工期、环境政策等。 - 初步筛选候选区域
根据宏观经济、区域发展政策及行业聚集度等条件,初步圈定具备潜力的城市或地块。 - 构建评估模型(定性+定量)
综合运用AHP、评分卡、成本-效益分析等方法,将主观评价转化为量化决策依据,确保模型客观可靠。 - 数据采集与打分排序
对候选地进行指标量化,涵盖交通、成本、基础设施、政策支持、市场潜力等维度,打分后进行排序比较。 - 实地调研与多方协调
组织考察小组进行实地走访,验证数据真实性,同时对接政府、业主、合作方,考察实际可行性。 - 最终决策与可行性论证报告
综合所有信息与战略匹配程度,编制可行性报告并提交决策层审批,形成正式的选址决策结果。
七、未来趋势:智能选址的时代来临
随着人工智能(AI)、大数据和可持续发展理念的深度融入,选址决策正从传统的“经验驱动”走向“数据智能驱动”。未来企业在进行选址布局时,将更依赖实时信息采集、算法建模以及环境合规评估等系统工具,全面提升选址科学性与战略适应性。
7.1 AI与大数据选址
智能选址的核心在于数据获取、模型预测与算法优化三大能力的融合。通过API接口与爬虫技术,企业可以实时获取目标区域的关键变量数据,如房租水平、交通运价、劳动力价格、竞争门店密度、通勤效率等,并结合卫星图像、人口迁移趋势等外部数据源进行补充。
在数据驱动层面,机器学习可用于分析历史销售数据、消费频率与人口行为特征,预测区域需求密度、增长趋势甚至未来潜在热点区域。此外,强化学习算法能够对选址后的网络运营结构进行动态模拟,评估不同选址组合下的成本—服务最优解,辅助企业在多目标权衡中作出高质量决策。例如,电商平台可训练模型在满足时效的同时优化配送半径,从而最小化整体物流成本。
7.2 ESG与绿色选址
在“双碳”目标与ESG审计机制推进下,绿色可持续成为企业选址不可回避的战略议题。未来选址决策需重点关注碳足迹影响、交通拥堵程度及环境敏感性等维度。系统模型中应纳入单位运输碳排、能耗结构(是否具备清洁能源接入)、绿建认证等级等指标,量化评估选址节点的绿色水平。
例如,在配送中心选址中,企业不再仅关注交通便利性和租金成本,而会倾向选择配备太阳能发电、智能照明系统、雨水回收装置的绿色仓储园区,以提升可持续运营能力并满足ESG披露要求。未来,符合ESG合规与碳中和要求的选址项目将在投资、政策与市场形象上获得更多红利。
八、结语:一次选址,改变全局
选址不仅是一项运筹优化任务,更是企业战略落地的第一锚点。它是供应链系统设计的起点,也往往决定了物流效率、运营成本与客户满意度的上限。在AI与全球化加速变动的时代,我们更应理解——“选址”不是选一个点,而是构建一个适应未来的系统弹性与协同潜力。

📌 致远而谋:让每一次选址都具备系统眼光
在全球竞争与区域变化日趋复杂的背景下,选址已从“选择一个点”演变为“构建一个系统”。真正优秀的选址决策,应体现企业对未来趋势的洞察、对价值链的系统性把控,以及对长期战略协同的深度考量。一次科学的选址,可能决定整个企业的运营格局和未来走向。
参考文献与延伸阅读
- Daskin, M. S. (2013). Network and Discrete Location: Models, Algorithms, and Applications. Wiley.
- Chopra, S., & Meindl, P. (2018). Supply Chain Management: Strategy, Planning, and Operation. Pearson.
- Christopher, M. (2016). Logistics & Supply Chain Management. FT Press.
- Amazon Logistics White Papers.
- 《运筹学与供应链优化》——清华大学出版社。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号