系统论(十五)——复杂系统的计算视角：从细胞自动机到计算宇宙

在自然界与人类社会中，复杂系统无处不在：天气、经济、生态系统、交通流、社会网络……这些系统由大量简单个体相互作用而形成，却展现出远超个体行为的复杂涌现现象。长期以来，科学家试图用方程和模型来描述它们，但始终难以捕捉复杂性的全貌。斯蒂芬·沃尔夫勒姆提出了一个颠覆性观点：复杂性或许源于简单规则的计算过程。他通过研究细胞自动机，发现即使最简单的规则也能演化出高度复杂的结构与动态行为。这一计算视角不仅为复杂系统研究提供了新思路，也挑战了我们对自然法则与宇宙本质的认知。

---

一、引言

在自然界与人类社会中，复杂系统无处不在，它们展现出令人惊叹的组织结构、演化模式与涌现现象：

• 蜂群、蚁群、鸟群的集体协同行为；
• 金融市场的周期性波动与突发金融危机；
• 气候系统中不断形成的涡流、厄尔尼诺现象与极端天气；
• 甚至包括宇宙尺度下的星系形成、物质聚集与时空演化。

这些系统往往包含成千上万、甚至无数个基本个体，每个个体行为看似简单，但通过局部相互作用，整体却演化出高度复杂、不可预知且具有适应性的宏观行为。传统的微分方程、统计模型、概率系统在某些场景下虽然有效，但面对很多复杂系统的动态演化仍显捉襟见肘。
20世纪末至21世纪初，斯蒂芬·沃尔夫勒姆（Stephen Wolfram）提出了一个极具颠覆性的观点。他在其代表作《A New Kind of Science》（2002）中系统阐述：宇宙本身或许是一台遵循极为简单计算规则的巨大自动计算机器。在他看来，复杂性并非源自复杂规则，而恰恰可能源于极简的底层算法在长期迭代后的自然演化结果。
在本文中，我们将尝试站在计算的视角，探索复杂系统背后的计算逻辑，对复杂系统的核心思想进行系统性梳理，融合典型案例、数学模型与可视化模拟，力图揭开复杂系统背后潜藏的本质逻辑与统一框架，逐步走向“计算宇宙”这一前沿思想。

---

二、复杂系统的基本特征

在讨论复杂系统之前，我们首先需要理解：复杂性并非意味着混乱或无序，而是指多层次、多尺度、多变量之间复杂而有组织的动态关联。复杂系统往往展现出一些高度普遍性的核心特征：

2.1 涉及多主体的相互作用

复杂系统几乎都包含大量的基本单元或主体，这些个体彼此之间通过各种机制进行相互作用。这些作用通常具有非线性特征，意味着微小的变化可能被放大成系统性的效应，或者多个小变化可以叠加出意想不到的结果。个体之间的互动方式可以是合作、竞争、信息交换或局部适应性行为。

自然界中的鸟群、鱼群、蚁群便是典型代表。成千上万只鸟通过简单的邻域规则飞行，却能整体保持队形协调；蚂蚁通过信息素标记形成复杂的觅食路径；鱼群则通过位置调整避免捕食者攻击。这些生物个体虽然认知简单，但整体却表现出极高的协同性与适应性。

2.2 局部简单规则，整体复杂涌现

复杂系统的一个令人着迷的特征是：整体复杂行为可以由非常简单的局部规则生成。这种现象称为涌现（Emergence）。局部简单规则在大规模个体迭代与相互作用下，逐步累积出宏观层面的全新模式与结构。

康威生命游戏（Conway's Game of Life）提供了一个极为经典的例子。它仅有四条简单的元胞自动机规则，却可以在二维网格上演化出稳定结构、振荡图案甚至“滑翔机”与“滑翔枪”等复杂运动图形。生命游戏被誉为复杂系统研究的启蒙模型，展示了“简单规则-复杂现象”的迷人逻辑。

2.3 自组织现象

复杂系统常常具备**自组织（Self-Organization）**能力，即在没有中央控制或全局规划的情况下，系统通过内部机制自动形成高度有序的结构。这种现象背后往往存在反馈机制、局部适应、协同演化等机制驱动。

雪花结晶的六角对称性、贝壳表面的精美花纹、斑马身上的条纹图案，都是自组织现象的直观展现。这些结构并非由“设计师”规划，而是由分子尺度的物理与化学规则自动形成。

2.4 动态演化与非平衡状态

绝大多数复杂系统处于远离平衡的非平衡态。它们通过与环境持续进行能量、物质、信息的交换，在动态演化过程中不断产生新状态与新结构。复杂系统的演化轨迹往往表现出路径依赖性、敏感性与历史性。

气候系统在不断接收太阳能、释放红外辐射的动态平衡中产生风暴、飓风等复杂现象；金融市场则在无数交易者信息博弈与资金流动中形成价格波动、市场泡沫与突发危机。这些现象不仅复杂，而且常常无法被传统平衡理论充分解释。

---

三、沃尔夫勒姆的计算宇宙观

3.1 基本观点

斯蒂芬·沃尔夫勒姆（Stephen Wolfram）在其里程碑式著作《A New Kind of Science》（2002）中提出了计算宇宙观（Computational Universe Hypothesis），为理解复杂系统提供了全新的视角。他认为：

• 自然界的基本规律本质上可以用算法和计算过程来描述。
  物理法则、化学反应、生物进化等宏观现象，其本质可以视为在特定规则下执行的计算程序。
• 简单规则能够演化出极其复杂的现象。
  不需要复杂起点，只要拥有合适的简单规则，在不断迭代中便可能涌现出高度复杂的图案与动态行为。这与传统科学追求复杂方程组的做法截然不同。
• 元胞自动机是描述自然复杂性的有力工具。
  通过元胞自动机，可以用极为简洁的模型揭示复杂现象的生成机制。例如，在一维元胞自动机中，像“规则30”这样的简单更新规则，就能在演化中展现出极其丰富、不可预测的复杂图样。

沃尔夫勒姆指出，这些简单模型不仅能够模拟自然现象，甚至可能揭示自然界底层的运行机制。他提出：整个宇宙可能本身就是一台在执行简单规则的大型计算机。

3.2 元胞自动机简介

元胞自动机（Cellular Automata, CA）是沃尔夫勒姆计算宇宙观的重要建模工具，其基本构成包括：

• 离散空间格点：通常以一维或二维网格表示，每个格点称为“元胞”；
• 有限状态：每个元胞在每一时刻只能处于若干个有限状态之一（如0或1）；
• 局部规则更新：每个元胞的新状态只依赖于其当前状态与邻域内其它元胞状态；
• 同步迭代：所有元胞在每一轮迭代中同时更新，形成演化图景。

正是这种简单而统一的规则框架，使得元胞自动机成为研究复杂系统、模式形成、混沌现象乃至生命本源的重要理论平台。

典型模型：一维元胞自动机 Rule 30

import numpy as np
import matplotlib.pyplot as plt

rule_number = 30
rule_bin = np.array([int(x) for x in np.binary_repr(rule_number, 8)])

def rule(left, center, right):
    index = 7 - (left*4 + center*2 + right)
    return rule_bin[index]

N = 101
steps = 50
array = np.zeros((steps, N), dtype=int)
array[0, N//2] = 1

for t in range(1, steps):
    for i in range(1, N-1):
        array[t, i] = rule(array[t-1,i-1], array[t-1,i], array[t-1,i+1])

plt.imshow(array, cmap='binary')
plt.title("Rule 30")
plt.show()

---

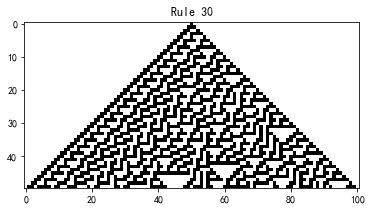
四、经典复杂系统案例解析

4.1 鸟群集群模型 (Boids 模型)

年轻时的帕里西教授曾在罗马火车站观察鸟群。通过统计物理，他总结出三条基本规则：

• 邻近：靠近视野中的邻居；
• 对齐：与邻居保持一致方向；
• 分离：避免碰撞。

Boids模型模拟 (简化版)

import numpy as np
import matplotlib.pyplot as plt

# 增加两行：支持中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']  # 设置中文字体为黑体
plt.rcParams['axes.unicode_minus'] = False    # 解决负号显示问题

N = 30
pos = np.random.rand(N,2) * 100
vel = (np.random.rand(N,2) - 0.5) * 10

for t in range(50):
    for i in range(N):
        neighbors = pos[np.linalg.norm(pos - pos[i], axis=1) < 15]
        if len(neighbors) > 1:
            vel[i] += 0.01 * (np.mean(neighbors, axis=0) - pos[i])
    pos += vel
plt.scatter(pos[:,0], pos[:,1])
plt.title("Boids群体行为模拟")
plt.show()

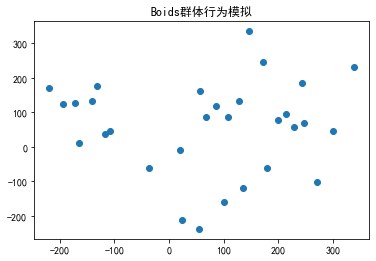
4.2 鱼群捕食模型

在自然界中，鱼群在面临捕食者威胁时会展现出极具视觉冲击力的集体规避行为。当捕食者逼近时，个体鱼根据周围邻居的位置和速度快速调整方向，形成高速旋转、扩散、收缩等复杂动态结构。看似无序的逃逸背后，其实遵循着简单的局部互动法则：保持适当距离、协调移动方向、避免碰撞。在这种局部规则作用下，鱼群整体自组织出复杂队形，不仅提升了逃生概率，也使捕食者难以锁定单一目标。研究表明，模拟这一过程的Boids模型或追逐-逃逸模型，在计算实验中能成功复现类似场景。

4.3 蚁群觅食路径

蚂蚁个体认知与计算能力有限，但它们借助信息素实现了高效觅食。每只蚂蚁在移动过程中释放微量信息素，若在某条路径上频繁成功找到食物返回，信息素浓度将持续增强。其他蚂蚁更倾向于沿高浓度信息素路径移动，进一步强化该路径，最终形成全体蚂蚁共享的最优食物通道。这种正反馈机制展现了典型的自组织优化过程。蚁群觅食也成为现代优化算法如**蚁群算法（Ant Colony Optimization, ACO）**的重要灵感来源，被广泛应用于物流、网络路由与组合优化领域。

4.4 滑坡与森林火灾模型（临界状态）

在滑坡、雪崩、森林火灾等自然现象中，系统通常长期积累应力或易燃物质，短时间内看似稳定。然而，一旦局部扰动触发，整个系统可能迅速演化为灾难性大规模事件。此类现象被称为自组织临界性（Self-Organized Criticality, SOC），其特征是：小事件频繁发生，而大事件则服从幂律分布。沙堆模型与森林火灾模型是研究这一现象的重要简化模型，有助于理解自然界与社会系统中的突发性灾变机制。

---

五、生命游戏：涌现复杂性的教科书模型

5.1 规则简介

康威生命游戏（Conway's Game of Life）由英国数学家约翰·康威（John Conway）于1970年提出，是细胞自动机研究中最具代表性的模型之一。生命游戏的世界是一个无限二维网格，每个格子（细胞）有两种状态：生（1）或死（0）。每轮迭代，根据邻近八个格子的状态决定下轮更新，规则极其简单：

• 繁殖：若某个死细胞恰好有 3 个邻居存活，则该细胞在下一代复活；
• 生存：若某个活细胞有 2 或 3 个邻居存活，则它继续存活；
• 死亡：若邻居数小于 2（孤独）或大于 3（过度拥挤），则该细胞死亡。

滑翔机	康威生命游戏中的较复杂演化模式	脉冲星

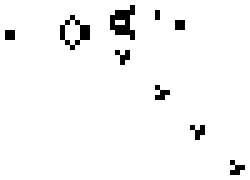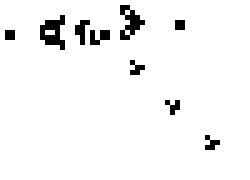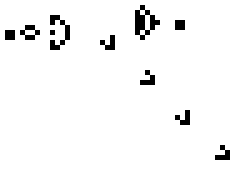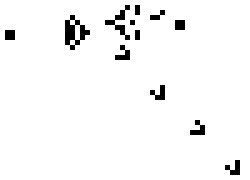5.2 经典结构

尽管规则简单，却能演化出丰富多彩的模式：

• 稳定体：如 block（方块）、beehive（蜂巢）、loaf（面包）等，在演化中保持不变；
• 振荡器：如 blinker（闪烁器，周期 2）、toad（蟾蜍，周期 2）、beacon（灯塔，周期 2）等，周期性变化；
• 滑翔机 (glider)：一个小型自移动结构，沿着对角线方向缓慢移动；
• Gosper’s glider gun：由比尔·高斯珀在1970年发现的第一个“滑翔机枪”，可以持续不断地产生滑翔机，被视为生命游戏中的重要突破。

生命游戏不仅是一种数学娱乐，更成为涌现（emergence）现象的经典教材。研究者利用它探讨复杂性、计算理论、人工生命与自然界秩序的起源等重大课题。它也间接印证了沃尔夫勒姆等学者的观点：复杂行为可以源于极为简单的底层规则。

5.3 Python模拟

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

N = 100
grid = np.random.choice([0,1], size=(N,N))

def update(data):
    global grid
    newGrid = grid.copy()
    for i in range(N):
        for j in range(N):
            total = int((grid[i, (j-1)%N] + grid[i, (j+1)%N] +
                         grid[(i-1)%N, j] + grid[(i+1)%N, j] +
                         grid[(i-1)%N, (j-1)%N] + grid[(i-1)%N, (j+1)%N] +
                         grid[(i+1)%N, (j-1)%N] + grid[(i+1)%N, (j+1)%N]))
            if grid[i,j] == 1:
                if (total < 2) or (total > 3):
                    newGrid[i,j] = 0
            else:
                if total == 3:
                    newGrid[i,j] = 1
    mat.set_data(newGrid)
    grid = newGrid
    return [mat]

fig, ax = plt.subplots()
mat = ax.matshow(grid)
ani = animation.FuncAnimation(fig, update, interval=50, save_count=50)
plt.show()

---

六、复杂系统的计算性哲学

6.1 沃尔夫勒姆的主要断言

在《A New Kind of Science》中，斯蒂芬·沃尔夫勒姆提出了极具突破性的哲学观点，即自然界本身就是一个庞大的计算过程。传统科学总是试图寻找描述自然现象的方程、模型与连续函数，而沃尔夫勒姆则提出：

• 自然界的本质是计算：无论是星系的形成、天气系统的演化，还是生物体内的分子反应，本质上都是某种形式的计算过程在起作用。
• 计算等价性原则（Principle of Computational Equivalence）：绝大多数非平凡系统，其计算能力在本质上是等价的。即：当系统复杂到一定程度时，无论规则多么简单，其行为与图灵机（可计算性极限）相当，都可以模拟任何其他复杂计算过程。
• 简单规则可生成复杂现象：自然界无需极其复杂的底层定律，通过简单的局部规则反复迭代，就可自然演化出极其复杂的全球性行为。这与常识中的“复杂系统需要复杂规则”完全不同。

这一观点颠覆了人们对自然规律的传统理解，把重点从方程与连续模型转向离散计算与算法模型。

6.2 与传统物理学的区别

沃尔夫勒姆的计算性哲学与传统物理学在多个层面存在本质区别：

传统物理学	沃尔夫勒姆计算观
以微分方程为核心，依赖连续变量与极限过程	以离散计算系统为核心，强调状态有限性
模型依赖整体控制、全局描述	局部规则控制，系统分布式自组织演化
偏好平衡态与可解性	关注非平衡、非可解但可模拟的复杂演化
追求解析解与可预测性	强调模拟、演化与涌现现象

沃尔夫勒姆认为，自然界许多看似复杂的规律背后并不存在难以穷尽的公式，而是类似于计算机程序那样的简单规则通过大量迭代自然涌现复杂性。因此，模拟、实验和计算成为理解自然复杂系统的重要方法。

6.3 元胞自动机 vs 复杂系统

元胞自动机（Cellular Automata）是沃尔夫勒姆提出计算宇宙观的重要工具与模型。其基本特征：

• 系统由有限状态的格子组成；
• 按照局部邻域规则更新；
• 全局行为源于局部规则的反复迭代。

元胞自动机展示了**“简单规则 → 无限复杂性”**的核心理念。例如：

• 一维元胞自动机 Rule 110：这是最经典的元胞自动机之一。其规则极为简单，仅对当前单元与相邻单元状态的组合做出决策。令人惊讶的是，1994 年被证明具有图灵完备性，即可以模拟任意复杂的计算任务；
• 二维康威生命游戏：通过简单的生存、死亡、繁殖规则，演化出众多复杂、动态甚至具备计算功能的结构。

这些模型向我们展示了复杂系统研究的一种全新可能性：我们无需穷尽式描述所有细节，而是可通过简单规则复现系统的全局复杂行为。这种方法不仅应用于自然科学，也已广泛影响人工智能、金融建模、生态模拟等领域。

---

七、计算视角下的新科学前景

斯蒂芬·沃尔夫勒姆所提出的计算宇宙观不仅为复杂系统提供了崭新解释框架，也为多个学科的前沿研究带来了深远影响。计算性思维正逐渐成为跨学科科学探索的重要工具，推动着多个前沿领域的革新。

7.1 生物复杂性解释

在生物系统中，复杂性几乎无处不在。从分子水平到整体生命体，每一层级都蕴含着高度组织化与复杂演化过程。沃尔夫勒姆的计算视角在以下几个方面提供了重要思路：

• 基因调控网络：基因表达的调控并非简单线性过程，而是一个复杂的逻辑网络系统。每个基因的表达状态受到上游调控基因、外界环境等多方输入影响，形成类似离散自动机的动态网络。基因开关之间复杂的互作可以看作一种基于局部规则的大规模并行计算系统。
• 蛋白质折叠路径：蛋白质折叠问题长期被认为是生物物理学中的一大挑战。蛋白质链条在复杂的能量地形中通过局部相互作用最终折叠为稳定结构，这一过程可以类比为局部简单规则逐步推进形成复杂三维形态的计算演化过程。
• 神经网络突触联接：大脑神经元之间形成的突触网络展现出复杂的拓扑与信息处理能力。从局部突触可塑性、长时程增强、到整体脑区功能模块的形成，都体现了典型的自组织与复杂系统演化特征。

7.2 经济复杂性模拟

传统经济模型往往基于均衡假设与理性个体假设，难以解释市场波动、金融危机等复杂现象。计算复杂性方法为经济学提供了新的模拟与预测工具：

• 市场博弈系统：市场参与者之间存在复杂博弈行为，情绪、预期、博弈策略之间的相互作用可通过类似元胞自动机与博弈网络建模，揭示市场泡沫形成与破灭的内在机制。
• 代理人基础建模（Agent-Based Modeling）：将经济参与者视为独立的计算代理体，通过设定简单决策规则与互动机制，模拟出宏观经济指标、产业演化、政策效应等复杂动态过程。该方法在金融市场仿真、宏观调控政策评估中已有广泛应用。

7.3 人工智能与深度学习的本质关联

人工智能与复杂系统本质上存在天然联系：

• 神经网络层级计算即嵌套复杂系统自组织结构：深度神经网络依赖多层嵌套计算单元，通过局部连接与迭代训练，逐渐形成高度复杂的特征提取与模式识别能力。这一过程与复杂系统中局部规则演化出全局秩序高度相似。
• 规则简单 → 层次复杂：尽管单个神经元的激活函数、加权和计算极其简单，但多层迭代构建出的复杂决策边界却展现出惊人的智能表现，印证了简单计算规则涌现复杂行为的核心理念。

7.4 宇宙学可能新图景

沃尔夫勒姆的计算宇宙观甚至试图重构我们对宇宙起源与演化的理解：

• 宇宙大爆炸即为某一简单程序之初始状态：宇宙诞生之初或许仅由极为简单的初始规则或图结构启动，类似于程序运行的初始输入。
• 宇宙演化即为复杂系统计算性展开：从最初的极简状态，通过持续迭代与规则演化，逐步发展出粒子物理、星系形成、生命诞生、意识演化等一系列高度复杂的自然现象。宇宙在本质上可能正是一个运行中的巨大计算过程。

---

总结

复杂系统并非神秘莫测，而是可以通过明确的计算模型加以揭示和理解。沃尔夫勒姆的计算视角为我们提供了一种突破传统学科界限的全新思维框架，强调了简单规则经过大量迭代计算后，能够产生极其复杂且丰富的行为模式。这种从局部出发的多主体交互机制，使得系统整体能够自组织并涌现出宏观的秩序与结构，超越了传统因果关系的线性思维。尤其是离散计算模型的引入，挑战了经典连续模型的统治地位，暗示自然界和社会系统的运行更像是一台巨大的计算机，其根本规律或许就是基于离散状态和规则的演化。
这一视角不仅为自然科学领域的研究注入了新的活力，如生物学中的基因调控网络、神经系统的复杂连接，也为经济学、社会学中的多主体博弈、网络效应提供了更具解释力的理论工具。同时，人工智能的发展亦可从计算复杂性中汲取灵感，促进算法设计与智能系统的创新。更进一步，哲学对“秩序与混沌”、“自由意志与决定论”的思考，也将在计算视角下获得新的诠释和启示。总之，计算视角的兴起，不仅是一种方法论的革新，更可能成为跨学科融合和知识创新的关键驱动力，推动我们对世界本质的认知达到前所未有的深度。

---

Sakana AI联合来自MIT、OpenAI、瑞士AI实验室IDSIA等机构的研究人员，提出了“自动化人工生命搜索”（ASAL）的新算法，旨在利用大模型自动化地探索人工生命（ALife）领域中的模拟空间。这意味着不需要繁琐的手工设计，只通过描述，AI就能发现全新的人造生命体，参考上图。本文如同一次思维训练营，若读者意犹未尽，推荐研读沃尔夫勒姆《A New Kind of Science》原著，以及观看其近年在Wolfram Physics Project中的最新研究成果。

---

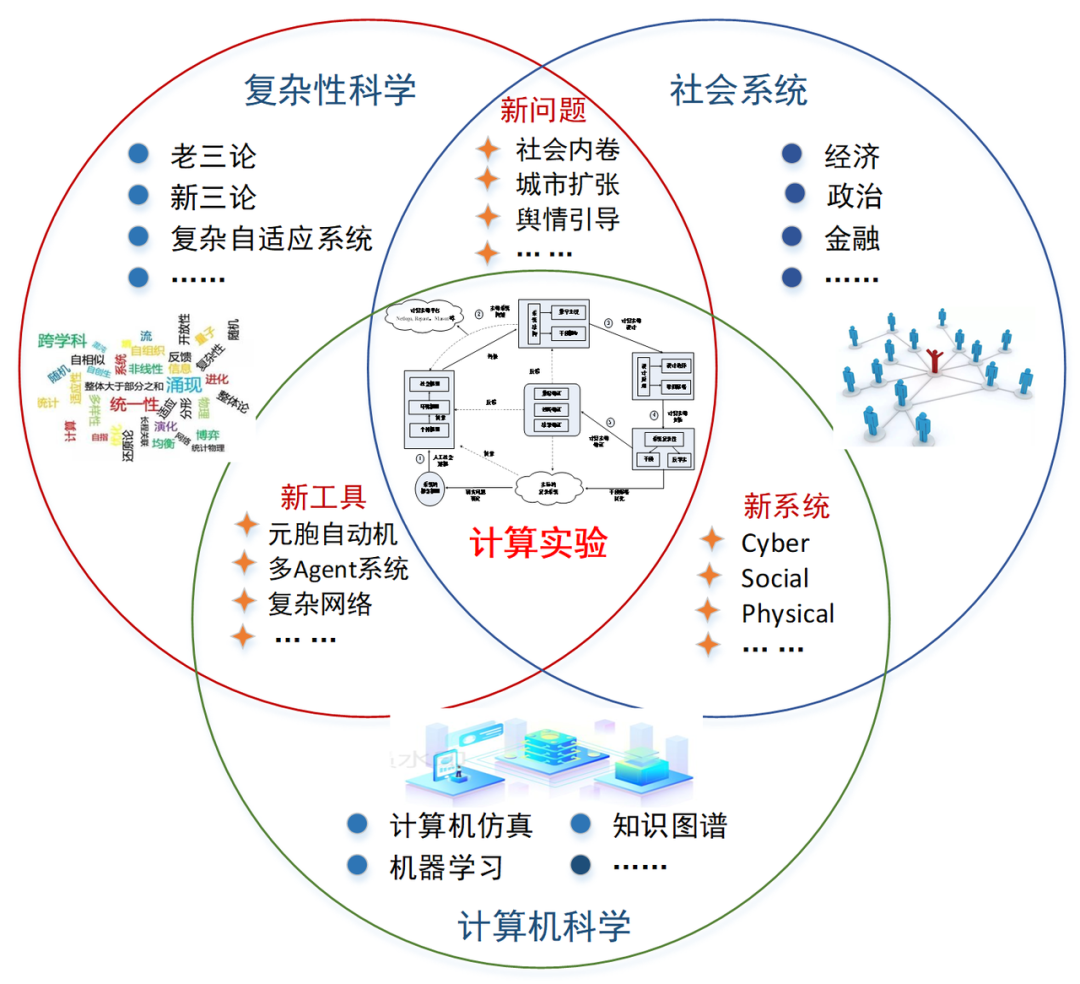
计算实验融合复杂性科学、社会系统与计算机科学，成为研究复杂现象的重要工具。复杂性科学关注老三论（耗散结构、协同学、突变理论）、新三论（混沌、分形、人工生命）及复杂自适应系统，揭示系统非线性、涌现与自组织特性。社会系统涵盖经济、金融、政治等，聚焦城市扩张、舆情演化与社会内卷等新兴问题。计算机科学则提供高性能计算、机器学习与智能算法支撑。当前，计算实验广泛采用元胞自动机、多Agent系统与复杂网络模型，模拟微观行为与宏观模式的互动机制。最新发展中，AI驱动的计算实验（如深度强化学习、多智能体协同仿真）正快速兴起，同时，Cyber-Social-Physical Systems（CPS）框架推动人-机-物深度融合，助力智慧城市、政策仿真与社会治理的前沿探索。

---

参考文献

[1] Wolfram, S. (2002). A New Kind of Science. Champaign, IL: Wolfram Media.
[2] Parisi, G. et al. (2014). Collective behavior in animal groups: Theoretical models and empirical studies. Proceedings of the National Academy of Sciences, 111(Supplement 3), 10866–10871.
[3] Conway, J. H. (1970). The Game of Life. Scientific American, 223(4), 4-9.
[4] Mitchell, M. (2009). Complexity: A Guided Tour. Oxford University Press.
[5] Wolfram, S. (2020). A Project to Find the Fundamental Theory of Physics. Wolfram Media.