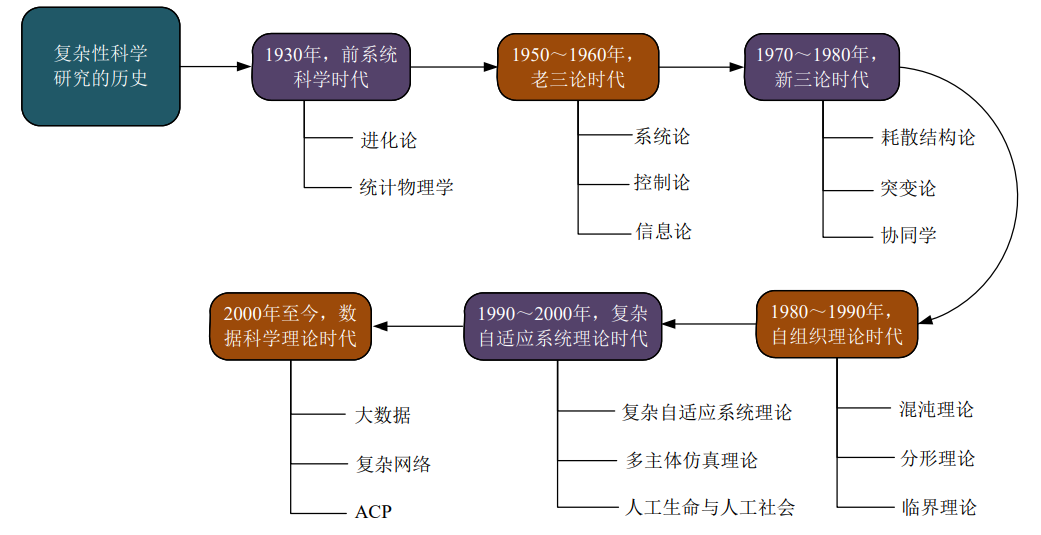
系统论(十四)——社会经济演化的密码：耗散结构、突变与协同学理论解读

在当代复杂系统科学中，理解社会经济系统的演化机理愈发重要。不同于传统线性分析，现代社会经济系统呈现出强烈的非线性、动态性与多稳定性特征，其行为往往无法用简单因果逻辑解释。从能源危机到金融动荡，从技术跃迁到组织管理，从政策失效到社会动荡，背后都隐藏着复杂系统内部的演化逻辑。耗散结构理论揭示了远离平衡状态下系统自组织有序的生成机制；突变理论刻画了系统在连续变化中出现突发跃迁的临界特性；协同学则揭示了微观要素如何在序参量主导下形成宏观秩序。这里将系统梳理这三大系统理论的核心思想、数学模型与社会经济应用实践，尝试为理解当代复杂社会经济现象提供系统性的理论框架与管理启示。

---

第一部分 耗散结构理论及其社会经济应用

1.1 理论综述

什么是耗散结构？

耗散结构（Dissipative Structure）理论由比利时物理化学家普里高津（Ilya Prigogine）在20世纪60年代提出，主要研究开放系统在远离平衡态时，通过与外界的能量、物质和信息交换形成有序结构的机制。
与传统的热力学平衡理论不同，耗散结构强调开放性、非平衡性和非线性，揭示了在外界扰动和系统内部非线性反馈机制共同作用下，系统能够从无序中自发诞生新的有序状态。这一理论的提出极大地拓展了人类对复杂系统组织演化的理解，被誉为“第二热力学革命”。

核心特点

特征	描述
开放性	系统与外部环境进行持续的能量、物质与信息交换
远离平衡	系统处于稳定平衡状态之外，存在持续的通量流动
非线性	系统内部变量间存在非线性耦合与反馈机制
自组织	在特定条件下形成新的有序宏观结构
突变性	系统在临界条件下可能发生突然的跃迁或重组

耗散结构的提出背景

• 对经典热力学平衡态理论的突破
• 对生物系统、生态系统、社会系统的动态演化现象提供合理解释
• 复杂系统建模与管理的基础性理论支撑

1.2 形成机制与数学描述

非平衡热力学基础

耗散结构产生的必要条件是系统处于远离平衡态。传统平衡态下的熵增原理依然成立，但在远离平衡的开放系统中，熵流可以通过以下方式表达：

\[\frac{dS}{dt} = \left( \frac{dS}{dt} \right)_{内} + \left( \frac{dS}{dt} \right)_{外} \]

其中：

• \(\left( \frac{dS}{dt} \right)_{内} \geq 0\)：系统内部熵产
• \(\left( \frac{dS}{dt} \right)_{外}\)：熵流入或流出系统

当外界输入足够负熵（信息、能量或组织性）时，系统可以在整体熵增的背景下形成局部有序结构。

非线性反馈与涨落放大

在远离平衡态下，系统内部存在微小涨落。通过非线性正反馈机制，某些涨落被放大并演化为新的宏观结构。

flowchart LR A[远离平衡] --> B[微小涨落] B --> C[非线性反馈放大] C --> D[有序结构诞生]

分岔与相变

耗散结构的形成往往伴随分岔现象：

• 控制参数缓慢变化
• 到达某临界点（分岔点）
• 系统自发选择其中一个稳定有序态

其数学描述往往使用分岔理论、非线性微分方程与稳定性分析进行建模。

1.3 典型案例

耗散结构理论自提出以来，在多个自然科学与社会科学领域中得到了广泛而深刻的应用。以下结合物理化学、生物生态、工程管理等不同领域，系统性梳理典型案例，以加深对耗散结构形成与演化机制的理解。

物理化学领域典型耗散结构案例

（1）贝纳德对流

当一薄层液体从下方均匀加热时，在温差达到临界值之前，液体内部以热传导方式缓慢传递能量。然而，当温差超过某一临界点后，系统突然出现六边形对流胞图案，形成有序的热对流运动。这一现象正是耗散结构的典型代表：液体系统在持续能流输入下远离热力学平衡，通过非线性相互作用实现自组织有序模式。

（2）化学振荡反应（BZ反应）

布里吉金斯基—左雅托夫斯基（BZ）反应是一类典型的化学振荡系统，反应物浓度在时间上呈现周期性涨落，形成颜色周期变化的视觉效果。BZ反应表明，开放的化学体系在持续物质流动和反应过程中可形成稳定的时空有序结构，即耗散结构的动态体现。

（3）激光系统模式形成

在激光谐振腔内，泵浦能量的持续输入将系统推入激发态。当能量输入超过阈值后，光子通过受激辐射过程发生相干放大，形成特定频率与模式的稳定激光输出。激光模式竞争、模式锁定与模式跳跃等现象，均体现了系统在非平衡条件下形成稳定耗散结构的动态演化规律。

生态生物领域典型耗散结构案例

（1）细胞膜与分子自组装

在生物分子系统中，磷脂双分子层自动排列形成细胞膜，是典型的自组织现象。分子间的疏水效应、静电相互作用等微观非平衡过程，驱动系统形成具有功能性的边界结构，为生命活动提供了基础性耗散平台。

（2）生态系统多样性维持

生态系统通过光合作用、食物链能量流动与物种竞争协同，实现物种多样性与系统稳定性。能量与物质的持续输入输出维持了系统远离平衡，种间关系、生态位划分与适应演化机制共同塑造了耗散性的生态有序格局。

（3）生物进化中的新物种涌现

物种在长期环境变化与基因突变中形成新的生物形态，表现出适应性进化与多样性扩展。新物种的形成可视为系统在突发扰动与适应性反馈下产生新的稳定耗散结构形态，生物多样性的产生即是一种耗散性的系统重组与进化。

工程管理领域典型耗散结构案例

（1）城市交通系统组织模式

城市交通系统作为典型复杂耗散系统，在交通流量、信号灯调度、道路布局、出行行为等多重因素共同作用下形成动态有序流动。交通拥堵现象则是当系统负荷超过临界阈值后形成的耗散性堵塞结构。智慧交通控制技术正是实时调节控制参数，维持系统稳定运行的典型管理实践。

（2）工业生产组织秩序

现代工业生产体系高度依赖动态物流、柔性制造与实时调度机制。订单流、物料流与信息流之间复杂的反馈耦合形成生产秩序的动态组织模式。生产过剩、物料积压与供应链断裂均可视为耗散结构失稳的表征。因此，供应链协调与智能制造优化正是耗散结构理论在工业管理中的直接应用场景。

1.4 社会经济应用实践与启示

耗散结构理论为理解和管理复杂社会经济系统提供了全新视角。其应用不仅揭示了系统有序演化的可能性，也为政策调控与管理创新提供了重要启示。

1.4.1 社会经济系统的耗散属性深化

社会经济系统具备高度开放性、远离平衡性、非线性反馈性及自组织性，其主要耗散特征表现在：

• 要素多元开放交换：商品、资本、信息、文化、技术等多种要素持续流入流出系统；
• 政策调控下的非平衡动态：货币政策、财政政策、国际局势变化不断重塑系统运行平衡；
• 复杂多重反馈链条：消费者预期、资本流向、金融创新、技术进步等因素形成非线性正负反馈机制；
• 结构性自组织现象普遍存在：如产业升级、技术标准确立、区域经济整合、治理架构演化。

1.4.2 实践案例扩展

（1）产业集群与创新生态系统演化

科技产业集群的发展正是典型耗散结构自组织的社会经济体现。以硅谷、深圳、慕尼黑等科技创新中心为例：

• 人才、资本、技术、市场不断流入形成高能流状态；
• 初创企业、孵化器、投资机构、政策扶持形成正反馈回路；
• 在关键控制参数（如知识产权制度、风险投资机制）良好调节下，系统演化出高度自组织的创新网络；
• 技术标准和主导产业链条成为新有序结构的稳定核心；
• 知识溢出效应进一步强化系统稳定性，形成“创新磁场”现象。

以深圳为核心的华为产业链展示了耗散结构下的创新集群协同演化：华为作为技术龙头吸引了大量上下游企业、研发机构与高端人才聚集，资本市场持续投入，政策上出台产业专项支持，形成正反馈式的持续扩张。其5G、AI、芯片等核心技术标准在此生态圈内部快速迭代形成产业标准，系统涌现出强大的技术自组织能力，使深圳成为全球通信与智能制造的重要中心。

（2）金融市场泡沫与系统性崩溃

金融市场常呈现典型的耗散结构性涨落与失稳现象：

• 正反馈机制导致泡沫膨胀（资产上涨→投资热情上升→更多资金进入→资产继续上涨）；
• 当控制参数如杠杆率、利率、信贷宽松度接近系统极限时，微小扰动（如信心变化）便可引发剧烈调整；
• 金融危机爆发实质上是耗散结构的临界崩溃状态；
• 监管政策应关注正反馈放大效应，设计合理“缓冲阈值”以防系统性坍塌。

日本80年代金融市场高速扩张，低利率政策与宽松信贷驱动房地产与股市价格暴涨。资产价格飙升形成强烈正反馈循环，但监管未能有效控制杠杆与信贷扩张。90年代初泡沫破裂，银行坏账激增、信贷冻结，经济长期陷入“失去的二十年”，呈现典型耗散结构崩溃特征。

（3）城市交通组织中的耗散性调控

城市交通通过信号灯调度、路径引导、出行需求管理维持动态交通秩序：

• 系统负荷（车流量）为关键控制参数；
• 超载时自组织性失效，表现为拥堵带宽放大；
• 智慧交通系统利用实时数据反馈动态优化信号控制、诱导路线、限流调度，有效延长系统有序状态；
• 城市交通治理的核心在于设计合理的动态调整机制，维持远离临界堵塞区的系统运行区间。

新加坡采用ERP动态道路收费系统、实时交通流量监控、智能信号调度等措施，根据交通负荷实时调整出行成本与流量控制，成功避免了交通系统过载失稳，大幅降低了高峰期拥堵。其动态定价与智能调度构成有效耗散调控，维持交通系统稳定高效运行。

（4）宏观经济周期波动的耗散性本质

宏观经济系统波动本质上是周期性耗散结构演化的反映：

• 经济扩张期：投资、消费、信心等正反馈共振推动增长；
• 经济衰退期：预期转弱、资本收缩、消费萎缩形成负反馈萎缩；
• 政策调控通过调节关键控制参数（货币利率、财政赤字、汇率政策等）干预系统演化路径；
• 理解经济周期的耗散结构特性，有助于更科学设计反周期政策工具。

全球金融危机爆发后，中国迅速出台4万亿财政刺激计划及宽松货币政策，通过投资拉动、基础设施建设等手段调节关键控制参数，激发投资与消费正反馈链条，实现经济快速反弹。这一过程展示了通过政策干预控制经济耗散系统演化路径的典型实践。

（5）数字平台经济中的耗散性增长机制

数字经济平台（如电商、社交媒体、共享出行等）展现出强烈的耗散结构演化特征：

• 用户规模、数据流量、算法优化形成正反馈循环；
• 数据驱动的网络效应极易放大平台优势，形成规模主导型平台寡头格局；
• 数字治理需合理设计平台控制参数（如算法公平性、数据隐私规则、竞争政策）避免系统性风险积累。

抖音平台利用精准推荐算法、短视频内容生态、流量分发机制形成强大的正反馈系统。用户活跃度提升带动内容供给扩张，算法训练精度随数据增加不断优化，平台粘性迅速增强，最终在短时间内形成全球性流量寡头。抖音的算法驱动型耗散演化清晰展示了数字平台经济的非线性增长特征。

1.4.3 管理启示深化总结

管理领域	关键启示
组织管理	建立组织内部自组织激励机制，提升韧性与适应性
政策制定	政策即控制参数动态调整，需设定合理调控窗口
风险管理	正确认识系统失稳阈值与正反馈放大效应
创新系统	构建积极反馈的创新扩散与协同机制
城市治理	设计实时反馈与动态调节的智能治理模型

组织管理：激发自组织活力，增强适应韧性

在复杂多变的市场与技术环境中，组织需具备高度适应性。通过建立自组织激励机制，如授权式管理、跨部门协同、学习型组织文化，可促使员工自主发现问题、主动创新与动态调整。韧性组织能够在环境剧变时快速完成资源重组，化解风险，形成内生秩序。例如，许多高科技企业采用小团队自治+开放创新平台，有效应对了技术快速更迭的挑战。

政策制定：动态调整控制参数，避免极端偏离

在宏观经济与公共管理中，政策本质上就是对关键控制参数的干预。合理设定利率、汇率、税收、产业准入、环保标准等政策工具的调控区间，可有效稳定系统运行，防止系统偏离至不可控状态。例如货币政策通过动态调节利率与货币供应量，既刺激经济活力，又防止通胀与泡沫累积。政策制定需实时监测系统反馈，灵活微调，避免僵化滞后。

风险管理：关注系统失稳阈值与正反馈放大机制

复杂系统中的许多灾难性事件源于正反馈的持续放大跨越临界阈值。有效的风险管理需识别系统中最具敏感性的控制参数及潜在放大通道，提前设立缓冲机制。例如，金融机构的资本充足率管理、流动性监管即是对杠杆放大的提前抑制；供应链中的多元采购与冗余库存设计，也是缓冲风险集中爆发的有效机制。

创新系统：构建健康的扩散与协同反馈机制

创新扩散本身具有典型的正反馈特征。通过政策引导、产业联盟、知识产权保护、创新孵化平台等方式构建良性创新扩散机制，可放大技术溢出效应、降低创新失败率，提升整体创新效率。例如，硅谷的开放式创新生态、高校与企业协作平台正是协同创新反馈系统的典范。

城市治理：设计智能反馈与动态调节机制

现代城市运行复杂高度耦合，智慧城市建设通过物联网、大数据、AI算法等手段，实时监控交通流量、能源消耗、公共安全等关键运行参数，并及时反馈调整调控策略。例如，新加坡智慧交通与北京冬奥期间的智能能源调度系统，均展现出实时动态优化下的耗散结构稳定调控能力。

1.4.4 政策设计启发

• 保持系统开放性：引导要素跨界自由流动，防止因封闭僵化导致系统脆化；
• 精准监控控制参数：动态跟踪金融杠杆、房地产泡沫、技术集中度等系统性指标；
• 平衡正负反馈机制：既要利用正反馈促进发展，又要设立逆周期缓冲区避免系统失稳；
• 增强制度弹性与韧性：设计灵活政策工具，保障系统在外部冲击下具备自我修复能力；
• 培育复杂系统思维能力：提升决策者对非线性动态系统的理解力与干预精准度。

在社会经济复杂系统中，政策制定不再是线性因果调节，而需兼顾系统性、非线性与动态演化规律。首先，保持系统开放性至关重要。开放的资源、信息、资本与技术流动可为系统注入新鲜能量，避免内循环闭塞所带来的僵化与系统熵增。同时，精准监控控制参数成为动态治理的重要前提。借助大数据、AI监测工具，实时捕捉如金融杠杆率、债务水平、技术集中趋势、财富差距等敏感指标，有助于提前识别系统风险积聚。
其次，政策需在平衡正负反馈机制间灵活调节。正反馈可加速经济成长与创新扩散，但过度放大将酿成系统性危机。因此应设置逆周期调节缓冲区，在经济过热或技术泡沫形成时适度收紧政策，防止系统失控。同时，增强制度弹性与韧性，如设立财政稳定基金、灵活劳动力市场、产业转型缓冲机制，提升系统面向外部冲击时的吸收与自我修复能力。最后，提升决策者的复杂系统思维能力极为关键，使其能跳出线性直觉误区，全面把握多层次、多时滞、多因果交织下的政策影响路径，从而实现精准有效的宏观调控。

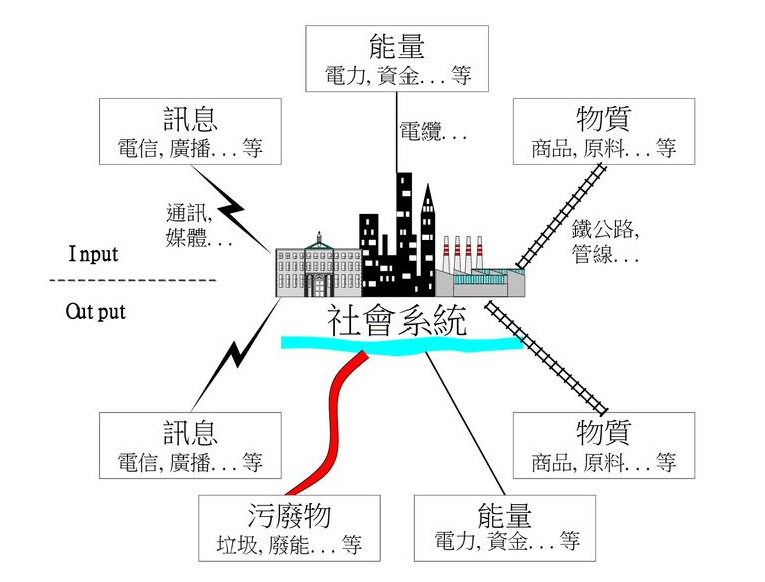
图中要素	耗散结构含义
输入 (Input)	系统从外界不断获取物质（商品、原料）、能量（电力、资金）、信息（通讯、媒体）。这是维持系统远离平衡的能流、物流、信息流。
社会系统本体	社会系统作为一个复杂的开放系统，对输入要素进行加工、组织、分配、管理，形成新的有序结构。
输出 (Output)	系统向外界输出有序成果（商品、信息服务等）与无序废弃物（垃圾、废能等），耗散掉部分输入能量以维持内部有序性。
信息回路	信息既作为输入，也是系统调控反馈的重要机制。通过媒体、通讯、广播等实时调节社会系统内部行为。
废弃物流	系统维持秩序的代价，即在能量、信息、物质转换中必然产生的熵增（即废弃物）。
物流与能流网络	通过铁路、管线、电缆等物理基础设施保障系统内部与外部的流通秩序。

整个社会系统维持有序的基本逻辑就是：
持续输入 → 系统加工组织 → 输出有序产品 + 耗散废弃物 → 维持整体有序结构

• 当输入充足、反馈及时、组织合理时，系统处于“稳态有序”；
• 当输入中断、反馈迟缓或控制参数失衡时，系统可能进入混乱或崩溃（即耗散结构失稳）。

1.5 小结

耗散结构理论为理解社会经济系统中的有序形成、波动演化、风险防控提供了坚实的理论支撑。
在快速变化的现代社会中，准确识别系统的控制参数、反馈机制与远离平衡程度，将是政策制定者、企业管理者与风险控制者的重要任务。

---

第二部分 突变理论及其社会经济应用

2.1 理论综述

什么是突变理论？

突变理论（Catastrophe Theory）由法国数学家勒内·汤姆（René Thom）在20世纪60年代提出，属于非线性动力系统分岔理论的重要分支，主要研究系统在平滑控制参数变化下可能发生的状态突变与跃迁行为。

突变理论强调：

即使外部条件连续平滑变化，系统内部结构可能因为非线性与多稳定性的存在，在某一临界点出现剧烈跳跃。

这种非线性跃迁现象广泛存在于自然、技术与社会经济系统中，例如滑坡、金融危机、政策失效、组织瓦解等。

突变现象的四大特征

特征	描述
多稳定性	存在多个稳定平衡态
不连续性	系统状态跳跃性突变
路径依赖	历史过程影响未来状态
临界敏感性	控制参数微小变化触发巨大后果

突变理论的意义

• 提供系统跃迁预测与干预框架
• 揭示系统非线性反馈失稳机制
• 描述复杂现象的突发性行为

2.2 基本模型与数学表达

突变势函数

突变理论核心在于构建系统的势能函数 \(V\)，系统趋向于使\(V\)极小：

\[V(x; \mathbf{a}) \]

其中：

• \(x\) 为状态变量；
• \(\mathbf{a}\)为控制参数向量；
• 系统演化遵循：

\[\frac{\partial V}{\partial x} = 0 \]

典型突变模型分类

类型	势函数表达	适用场景
折叠突变	\(V(x) = \frac{x^3}{3} - a x\)	最简单的跳变模型
吞噬突变	\(V(x) = \frac{x^4}{4} - \frac{a x^2}{2} - b x\)	金融崩盘、组织瓦解
笛卡尔突变	更高次势能	社会系统复杂跃迁
蝴蝶突变	\(V(x) = \frac{x^6}{6} + \frac{a x^4}{4} + \frac{b x^3}{3} + \frac{c x^2}{2} + d x\)	技术创新、群体心理演化

折叠突变模型举例

对于最基本的折叠突变模型：

\[V(x) = \frac{x^3}{3} - a x \]

平衡条件：

\[\frac{dV}{dx} = x^2 - a = 0 \]

可得：

\[x = \pm \sqrt{a} \]

当控制参数 \(a\) 变化时，系统可能从一个稳定状态突然跳跃至另一个状态，体现突变特征。

2.3 经典模型

物理自然领域

• 悬臂梁屈曲：逐渐施加外力，梁突然失稳弯曲；
• 地震断层滑移：地壳能量积累达阈值后突发释放；
• 液滴断裂：表面张力临界破裂形成小液珠。

生物生态领域

• 种群崩溃：捕食-被捕食系统在压力变化下种群灭绝；
• 疾病暴发：感染率超阈值后疫情爆发；
• 生态系统退化：环境压力诱发生态跃迁失稳。

工程技术领域

• 桥梁共振塌陷：风速缓慢提升突然诱发整体坍塌；
• 电力系统失稳：负荷变化导致大范围跳闸断电；
• 材料疲劳断裂：应力积累临界失稳断裂。

2.4 社会经济应用实践与启示

2.4.1 社会经济系统的突变属性

社会经济系统普遍存在复杂的突变现象，其典型机制包括：

• 多稳定性：经济繁荣与衰退并存；
• 阈值效应：金融泡沫、政策红线、资源承载力；
• 非连续演化：企业破产、社会运动、产业转型；
• 路径依赖：历史决策影响未来可行区间；
• 系统脆弱性：复杂反馈网络中存在崩溃链条。

（1）金融市场危机突变

• 牛市上涨 → 羊群效应 → 价格泡沫；
• 控制参数：杠杆率、利率、监管强度；
• 临界点：资金链断裂、信用崩溃；
• 表现：金融市场崩盘，资产价格急剧下跌。

2008年美国次贷危机即为典型的吞噬突变现象。长期低利率、信贷宽松与金融创新叠加放大了房地产泡沫，投资者普遍预期房价只涨不跌，形成羊群效应。当房价下跌引发大量次级贷款违约，资金链迅速断裂，整个金融系统信任崩溃，大量金融机构倒闭，全球金融市场陷入剧烈动荡。类似的突变机制也出现在2023年硅谷银行流动性危机事件中，市场预期的快速逆转引发存款集中挤兑，导致机构瞬间失稳。

（2）社会群体性事件

• 初期个别不满 → 情绪累积扩散；
• 控制参数：信息传播速度、制度回应能力；
• 临界点：临界事件触发群体行动；
• 表现：社会运动、骚乱、集体行动爆发。

例如2011年的**“阿拉伯之春”**，民众长期积累的不满在社交媒体迅速传播下形成情绪共振。制度缺乏有效回应成为关键控制参数失灵，最终以自焚等极端事件为临界触发点，引爆突发性的政权更迭与大规模社会动荡。突变理论揭示了系统在情绪涨落放大后的临界跳跃特性，体现了社会复杂系统的非线性敏感性。

（3）产业升级与技术突变

• 传统产业边际收益递减；
• 控制参数：技术突破积累、新商业模式兴起；
• 突变表现：新旧产业快速替代，形成蝴蝶突变模型；
• 案例：诺基亚陨落→智能手机快速统治市场。

诺基亚曾长期主导全球手机市场，但在智能手机技术体系（如苹果iOS生态与安卓开放平台）崛起后，传统功能机模式迅速失去竞争力。以智能手机为核心的新产业生态圈在短期内取代旧有体系，成为技术突变下的典型蝴蝶突变模型。类似突变正在自动驾驶、人工智能、量子计算等新兴产业中不断出现，显示出技术创新的非线性跃迁规律。

（4）环境与可持续发展突变

• 资源开发与污染积累；
• 控制参数：环境承载力、政策压力；
• 突变临界：生态系统不可逆退化；
• 案例：湖泊富营养化、沙漠化、气候灾变。

以太湖蓝藻爆发为例，长期工业废水与农业面源污染导致水体富营养化。随着污染物浓度突破环境承载力，湖泊生态系统从清水稳态跳跃到浑浊蓝藻稳态，形成典型折叠突变现象。类似的临界突变也广泛存在于全球气候系统中，如南极冰盖融化、亚马逊雨林退化等，一旦突破临界点将进入不可逆退化轨道。

2.4.3 管理启示

管理领域	启示内容
金融监管	识别潜在系统性风险积累
公共政策	设定合理制度缓冲区间
企业战略	预警产业转型突变窗口
环境治理	监测生态阈值与早期信号
危机管理	设计逆周期干预机制

2.4.4 政策设计启发

• 构建弹性边界：设立预警监测体系；
• 抑制正反馈链条：防止系统自加速失控；
• 识别临界窗口：及时干预避免跃迁发生；
• 强化制度适应性：增强系统缓冲与自愈能力。

2.4.5 突变早期预警指标示例

领域	预警信号
金融	杠杆率、违约率、信贷扩张速度
社会	舆情热度、群体不满分布、极端事件频率
企业	市场份额波动、创新失败率、客户流失曲线
环境	污染累积水平、生物多样性丧失速率

在突变理论应用中，早期预警指标体系对于防范系统性失稳具有重要意义。表中列举了四大关键领域中的典型预警信号。例如在金融系统中，杠杆率持续攀升往往预示着风险积聚，违约率上升与信贷扩张速度加快常成为泡沫破裂前的重要信号；在社会领域，舆情热度飙升、群体不满情绪蔓延及极端事件频率增加，可作为群体性事件爆发的前兆；对于企业管理，市场份额异常波动、创新项目频繁失败与客户流失曲线陡升，则可能预示企业竞争力衰退甚至面临商业模式崩溃的风险；在环境系统中，污染物积累与生物多样性快速丧失，常常标志着生态系统正逼近不可逆突变临界点。因此，构建跨领域、动态化的复合预警系统，是现代复杂系统管理的重要方向。

2.4.6 突变治理的系统思维总结

flowchart LR A[动态监测] --> B[识别反馈链条] B --> C[计算临界参数] C --> D[设计缓冲机制] D --> E[建立逆周期调节体系] E --> F[实时动态优化]

上述流程图展示了突变管理中系统性预防与动态干预的逻辑路径。首先，实施动态监测是基础，通过实时数据采集掌握系统运行状态。其次，需识别反馈链条，理清正反馈、负反馈与滞后环节，找出系统非线性放大机制的核心通道。第三步是计算临界参数，利用系统建模与模拟技术估算出可能导致突变的关键阈值与早期信号。随后，通过设计缓冲机制，如政策工具箱、多样化资源配置与应急预案，提升系统在外部冲击下的稳定承受力。再通过建立逆周期调节体系，在系统偏离均衡趋势初现时提前介入调节，有效平滑短周期波动，避免跨越临界阈值。最后实现实时动态优化，通过智能算法与多维数据融合，持续优化系统运行状态，构建具有高度适应性与韧性的动态管理体系。

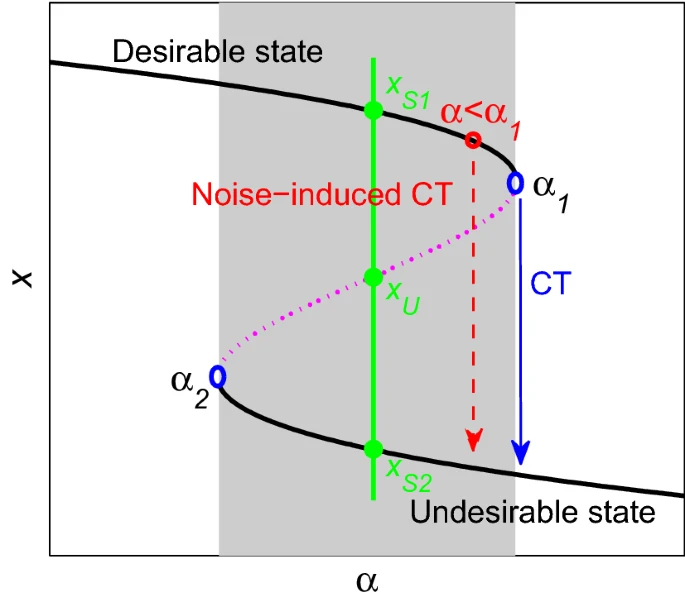
整体结构含义

这张图呈现的是双稳态系统的突变过程，横轴是控制参数 \(\alpha\)，纵轴是系统状态变量 \(x\)。

• 黑色曲线：稳定平衡态（上下两支）
• 紫色虚线：不稳定平衡态（鞍点）
• 绿色标注点：系统在正常情况下可能停留的稳定状态 \(x_{S1}\)​ 和 \(x_{S2}\)
• α1 / α2：两个典型的突变点（控制参数的临界值）
• Desirable state / Undesirable state：表示好的系统状态与不良系统状态

这是典型的折叠突变（Fold Catastrophe）或叫鞍结突变（Saddle-node bifurcation）。

核心突变机制

正常控制突变 (CT)

• 蓝色箭头所示的 CT（Catastrophe Transition） 指的是控制参数 \(\alpha\) 变化跨越 α1 时，系统从上支稳定状态 \(x_{S1}\)​ 突然跳跃到下支稳定状态 \(x_{S2}\)。
• 这是典型的控制参数驱动的突变，一旦超过临界值 α1，系统无法维持在原有的 Desirable state，会突然跳跃至 Undesirable state。
  噪声诱导突变 (Noise-induced CT)
• 红色虚线和红点显示了当 \(\alpha\) 还在 α1 之前（即远未到达控制临界值时），由于系统存在噪声、扰动、波动，导致状态 \(x\) 越过紫色虚线（不稳定鞍点）而突变到下支稳定态 \(x_{S 2}\)​。
• 这种情况在实际系统中非常普遍：小概率强扰动提前诱发突变，比如金融危机、社会骚乱、市场崩溃等。

2.5 小结

突变理论为理解社会经济系统中那些看似突如其来、实则长期积累的跃迁行为提供了重要数学框架。

在当今高度复杂的全球经济体系中：

• 决策者需具备突变理论视角识别脆弱性；
• 企业管理者需洞察产业临界点与转型窗口；
• 政策制定者需设计弹性制度缓冲系统；
• 公众需增强系统性风险意识与适应能力。

突变理论与耗散结构理论相结合，为复杂社会经济系统的理解、预测与治理奠定了坚实的系统科学基础。

---

第三部分 协同学理论及其社会经济应用

3.1 理论综述

什么是协同学？

协同学（Synergetics）是由德国物理学家赫尔曼·哈肯（Hermann Haken）在20世纪70年代提出的复杂系统理论，主要研究系统内各组成部分通过相互作用自发形成宏观有序结构的机制。

与耗散结构理论和突变理论相比，协同学更加关注：

• 各微观单元的相互协作机制；
• 有序结构产生的主导变量（序参量）；
• 多尺度、多层次的动态协调与演化规律。

协同学的核心思想

• 开放性与非平衡性：系统与环境持续交换；
• 非线性耦合：系统内部各要素相互作用复杂；
• 涨落放大：微小扰动在特定条件下快速扩展；
• 序参量控制：少数宏观变量决定整体有序性；
• 从无序到有序：系统呈现自组织涌现现象。

协同学的提出背景

• 传统控制论对复杂系统解释力有限；
• 描述激光系统的模式形成问题；
• 希望统一描述自然、技术与社会中的有序现象。

协同学与其他系统理论关系

理论	关注点	代表学者
耗散结构	能量流动与熵交换	普里高津
突变理论	状态跳跃与分岔	汤姆
协同学	多要素协同与序参量	哈肯

3.2 形成机制与序参量理论

序参量与从属参量

协同学认为：

在复杂系统内，只有极少数宏观变量（序参量）主导整体行为，其他大量变量（从属参量）迅速适应序参量演化。

形式化表达：

• 系统状态变量： \(\{x_i\}\)
• 主导变量：序参量\(\eta\)
• 其他变量：从属参量\(\{y_j\}\)

哈肯提出了从属原理：

\[y_j = f_j(\eta) \]

系统整体行为可用序参量的演化方程描述：

\[\frac{d\eta}{dt} = F(\eta, \lambda) \]

其中\(\lambda\)为控制参数。

Slaving Principle（奴役原理）

少数序参量"奴役"众多从属参量的演化行为，极大简化系统描述复杂度。

协同学三大定律

定律	内容
自组织定律	系统远离平衡时可能自发形成有序结构
序参量主导定律	少数序参量控制系统整体演化
从属原理	从属参量迅速适应序参量变化

稳定性与相位过渡

系统的有序状态往往表现为序参量的稳定值，在控制参数变化下，系统可能经历：

• 序参量分岔；
• 模式竞争；
• 新有序结构替代旧结构。

3.3 典型模型

物理自然领域

• 激光模式形成：激光系统在泵浦功率超过阈值后形成稳定光波模式；
• 贝纳德对流再解释：六边形对流胞作为序参量竞争的结果；
• 磁化相变：铁磁材料在居里点以下形成宏观磁化序列。

生物生态领域

• 细胞形态发生：基因调控下的器官发育模式；
• 鸟群鱼群同步运动：局部规则形成整体协调；
• 生态系统稳态转换：物种间协同维持多样性稳定。

工程技术领域

• 机器人编队控制：多智能体系统协同导航；
• 智能制造调度：多工位协同生产系统；
• 大规模并行计算：计算单元间任务分配协同优化。

3.4 社会经济应用实践与启示

3.4.1 社会经济系统的协同属性

社会经济系统本质上高度符合协同学特征：

• 大量微观主体（个人、企业、组织）参与；
• 存在显著宏观有序现象（产业格局、市场稳定、社会秩序）；
• 部分关键因素（政策、制度、技术、文化）作为序参量主导整体演化；
• 微观涨落可能在适当条件下被放大形成群体行为。

3.4.2 实践案例分析

（1）产业生态圈形成

• 微观行为体：企业、研发机构、政府、资本方；
• 序参量：产业技术标准、政策导向、供应链稳定性；
• 从属参量：产品型号、产能规模、价格调整；
• 协同结果：上下游企业形成稳定产业生态圈。

例如：新能源汽车产业链中动力电池技术标准的确立，尤其是宁德时代、比亚迪等龙头企业通过技术路径统一，带动了上游原材料（锂、钴、镍）、中游电池制造、下游整车厂商、充电基础设施等全链条的快速协同集聚，极大提升了产业效率与创新扩散速度，形成具有全球竞争力的产业生态系统。

（2）组织管理与团队协同

• 序参量：共同愿景、组织文化、领导风格；
• 从属参量：个人绩效、考核指标、行为规范；
• 协同结果：高效运转的组织行为系统；
• 涨落放大：管理创新或文化重塑可引发组织跃迁。

例如：海尔集团通过“人单合一”管理模式重塑组织文化，赋予员工充分授权，形成小微自组织单元，极大激发了员工创新活力与市场适应能力，组织整体在复杂市场环境下展现出强大的动态适应性，成为全球制造业组织创新的重要案例。

（3）社会稳定与治理协同

• 序参量：法律制度、公平机制、社会信任；
• 从属参量：个体行为、舆论态度、日常互动；
• 协同结果：制度协调与社会和谐；
• 失稳风险：制度信任崩溃可能诱发系统性动荡。

例如：新加坡在多元族群社会中通过法律制度严密设计、公平分配资源、强化公共服务质量，持续维系高水平的社会信任与秩序，形成了典型的制度协同稳定结构，有效避免了潜在的族群冲突和社会动荡，提升了治理韧性。

（4）宏观经济调控协同模型

• 序参量：货币政策、财政政策、国际汇率机制；
• 从属参量：通货膨胀、就业水平、消费信心；
• 协同结果：宏观经济动态平衡区间；
• 协同失败：如政策不协调导致滞胀或金融危机。

例如：2008年全球金融危机爆发后，美国政府通过联储宽松货币政策（QE）、财政刺激计划（如TARP救助）、国际货币合作等多维政策同步发力，有效避免了经济长周期衰退与失控，宏观调控体系展现出高度政策协同能力，成功将经济系统从边缘失稳状态拉回稳定区间。

（5）技术创新协同机制

• 序参量：技术标准、知识产权制度、研发投入政策；
• 从属参量：企业研发项目、创新投资行为；
• 协同结果：创新集群与技术扩散；
• 典型案例：AI产业、芯片产业、5G通信生态圈。

例如：在全球5G技术竞赛中，中国以政策推动、技术标准统一、产业链布局完整为支撑，形成以华为、中兴、大唐等为核心的设备制造集群，上游射频芯片、光模块、天线系统、基础算法软件企业同步发展，快速推动5G商用网络全球布局，形成了技术协同与产业扩散的国际领先态势。

3.4.3 管理启示

管理领域	启示内容
产业政策	确定关键序参量引导产业发展方向
企业管理	建立统一愿景与文化形成协同效率
政府治理	通过制度设计协调多元社会利益
公共治理	强化信任与社会资本的序参量地位
科技创新	规范技术标准提升协同创新能力

3.4.4 协同失效与风险防控

在复杂社会经济系统中，协同机制并非永远稳定。一旦关键条件发生偏离，系统极易由有序状态滑向混乱与失稳。其主要失效机制包括：

• 序参量失控或目标紊乱：当制度目标冲突、政策取向反复摇摆、产业方向失去统一性，核心序参量失去牵引作用，导致系统失序；
• 从属参量对序参量缺乏响应：如组织内部成员抵触改革，产业链上下游协调失灵，系统各子单元无法有效同步调整；
• 系统反馈通道受阻：信息滞后、反馈信号弱化、政策执行力不足等均削弱了系统自我修正能力；
• 外部强扰突破系统缓冲能力：如国际金融危机、重大疫情、地缘冲突等超预期冲击突破系统承载极限，诱发系统性崩溃。

针对上述潜在风险，协同管理需提前布局多重防控机制：

• 精准识别系统主控序参量，明确核心控制变量与关键目标；
• 增强反馈通路与适应性机制，提升实时信息采集与动态修正能力；
• 设立制度缓冲区与逆周期调节机制，提升系统抗压与修复能力；
• 强化序参量动态监控机制，确保核心变量稳定运行在安全区间，防范系统性跃迁风险。

3.4.5 协同优化的系统性设计框架

flowchart LR A[识别序参量] --> B[优化政策导向] B --> C[强化反馈机制] C --> D[提升系统韧性] D --> E[动态监测与适应调整]

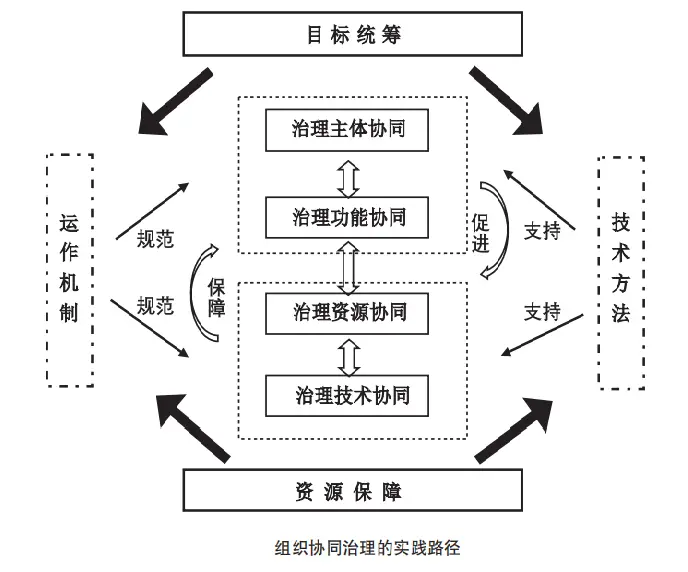
上述协同管理流程图展示了复杂系统中提升稳定性的基本路径。首先，识别序参量是管理的核心起点，需厘清哪些变量在系统演化中发挥主导作用，如产业政策、制度规范或技术标准。随后，通过优化政策导向，明确发展目标，减少内部目标冲突，确保序参量稳定牵引系统演化方向。接着，需强化反馈机制，构建及时、准确的信息采集与响应体系，保证管理者可实时捕捉系统变化并快速纠偏。通过此过程，进一步提升系统韧性，增强系统抵御内外部扰动的能力。最后，辅以动态监测与适应调整机制，实现持续监控与灵活干预，防止系统陷入协同失效与突发性崩溃，从而保障复杂社会经济系统长期健康运行。

3.4.6 协同学在数字经济中的新应用

在当代社会经济系统中，协同机制在多个前沿领域展现出强大应用价值。例如，在平台经济中，平台型企业通过用户、商家与算法的三元动态协同，形成供需高效匹配与规模快速扩展的闭环系统。以阿里巴巴与亚马逊为代表的全球平台巨头，正是依托精准算法推荐、活跃商家供给与海量用户参与，实现了平台生态的稳定繁荣。
在智慧城市建设中，交通、能源、安防、环境、政务等多系统协同集成是核心特征。新加坡智慧城市体系通过统一数据中枢和跨部门协同治理，保障了城市运行高效与居民生活质量的全面提升。
金融科技领域则依赖风控、信贷、客户管理三位一体的动态协同。蚂蚁金服、PayPal等通过大数据风控、智能授信与客户行为分析，实现了风险可控下的金融服务普惠性扩展。
在供应链管理中，信息共享、库存协同与物流调度成为核心协同要素。京东物流与亚马逊FBA通过多主体实时数据联动，实现了库存最优化、配送高效化与供应链弹性提升，增强了全球供应网络的稳定性与韧性。

3.5 小结

协同学理论在社会经济系统中应用广泛、前景巨大：

• 政策制定者需精准把握关键序参量；
• 企业管理者需构建良性组织文化与管理序参量；
• 公共治理需强化制度反馈与信任机制；
• 科技创新需设计协同生态与平台标准。

协同学为复杂系统治理提供了一种从微观多元走向宏观秩序的普适理论框架，在社会经济系统建模与治理创新中正发挥越来越重要的指导作用。

---

总结

在当代社会经济系统日益复杂、动态变化频繁的背景下，单一学科的分析工具已难以全面揭示其运行机理。上面详细梳理了耗散结构理论、突变理论与协同学三大复杂系统理论，从不同视角刻画了系统如何在开放、非平衡、多变量耦合条件下产生秩序、经历跃迁以及形成宏观协同行为。耗散结构理论强调能流驱动下的自组织与有序演化；突变理论揭示系统在连续变化下的非连续跳跃行为及其临界特性；协同学则揭示少数序参量如何主导系统整体行为形成稳定协同格局。三者在社会经济系统中的实践应用，既帮助我们理解金融危机、技术变革、组织管理、政策调控等现实问题的内在逻辑，也为政府、企业和管理者提供了前瞻性的风险预警与系统治理思路。未来，随着数据技术与系统模拟工具的不断发展，这些理论将更好地融合应用于宏观调控、组织管理、创新体系构建等多个社会经济前沿领域，助力提升系统韧性与治理智慧。

---

参考文献

1. Prigogine, I., & Stengers, I. (1984). Order out of Chaos: Man's New Dialogue with Nature. New York: Bantam Books.
   （耗散结构理论奠基性著作，详细阐释了非平衡热力学与自组织现象）
2. Thom, R. (1975). Structural Stability and Morphogenesis: An Outline of a General Theory of Models. Reading, MA: Benjamin.
   （突变理论的经典权威著作，系统建立了突变模型与几何学基础）
3. Haken, H. (1983). Synergetics: An Introduction. Nonequilibrium Phase Transitions and Self-Organization in Physics, Chemistry, and Biology (3rd ed.). Berlin: Springer-Verlag.
   （协同学理论的开创性专著，提出序参量与奴役原理）
4. Nicolis, G., & Prigogine, I. (1977). Self-Organization in Nonequilibrium Systems: From Dissipative Structures to Order through Fluctuations. New York: Wiley.
   （耗散结构与自组织系统的重要参考书，适合深入学习其数学基础）
5. Zeeman, E. C. (1977). Catastrophe Theory: Selected Papers, 1972-1977. Addison-Wesley.
   （突变理论在实际应用中的代表性论文集，包含大量社会科学与经济学应用实例）
6. Haken, H. (1987). Information and Self-Organization: A Macroscopic Approach to Complex Systems. Berlin: Springer-Verlag.
   （协同学在信息系统与复杂社会系统建模中的拓展性应用）