Spearman秩相关系数详解：理论、算法、代码

在统计学与数据分析中，衡量两个变量之间的相关性是一项基础而重要的任务。皮尔逊相关系数（Pearson correlation coefficient）由于其对线性关系的敏感性而被广泛使用，但它在数据不服从正态分布或存在极端值时表现不佳。为解决这一问题，Spearman秩相关系数（Spearman's rank correlation coefficient）作为一种非参数方法应运而生。
Spearman相关系数不要求数据服从特定分布，它基于秩（rank）而非原始值进行计算，能有效反映变量之间的单调关系。本文将系统介绍Spearman相关系数的背景、公式推导、计算方法、与Pearson的比较、Python与R语言实现方法及其在实际案例中的应用。

一、Spearman秩相关系数的定义与背景

1.1 Spearman相关系数的起源

Spearman相关系数，全名为Spearman等级相关系数（Spearman's Rank Correlation Coefficient），由英国心理学家查尔斯·斯皮尔曼（Charles Edward Spearman）于1904年首次提出。这一方法起初的目的是为了解决心理测量中的一个实际问题：在智力测验或其他心理测试中，往往获得的不是精确的数值变量，而是具有一定顺序性的评定结果。比如，一个学生的智力水平测试可能给出的是“高”、“中”、“低”等等级，或者直接按分数排名。这些数据本质上属于顺序型变量（ordinal variables），无法直接使用皮尔逊相关系数（Pearson correlation coefficient）来刻画变量之间的线性相关性。
Spearman认为，在这类问题中，更重要的是“排名之间是否一致”，也就是两个变量在排序上的一致性。例如，一个学生在数学和语文两个学科的排名是否相近，如果是，则可以认为两个变量存在较强的正相关；若排名差异极大，则相关性较弱甚至可能为负。基于这一思路，他提出了“秩”相关（Rank Correlation）的概念，并引入了Spearman秩相关系数来度量两个变量之间的“单调相关性”。从历史角度看，Spearman秩相关系数的提出是对当时统计方法在处理非正态数据和非度量尺度变量时的一种突破，开创了非参数统计方法的一个重要分支，至今仍广泛应用于心理学、教育学、生物统计学、社会科学等领域。尤其在现代数据科学中，Spearman系数也被用于处理非线性关系和鲁棒性分析，是皮尔逊系数的重要补充。

1.2 什么是秩相关？

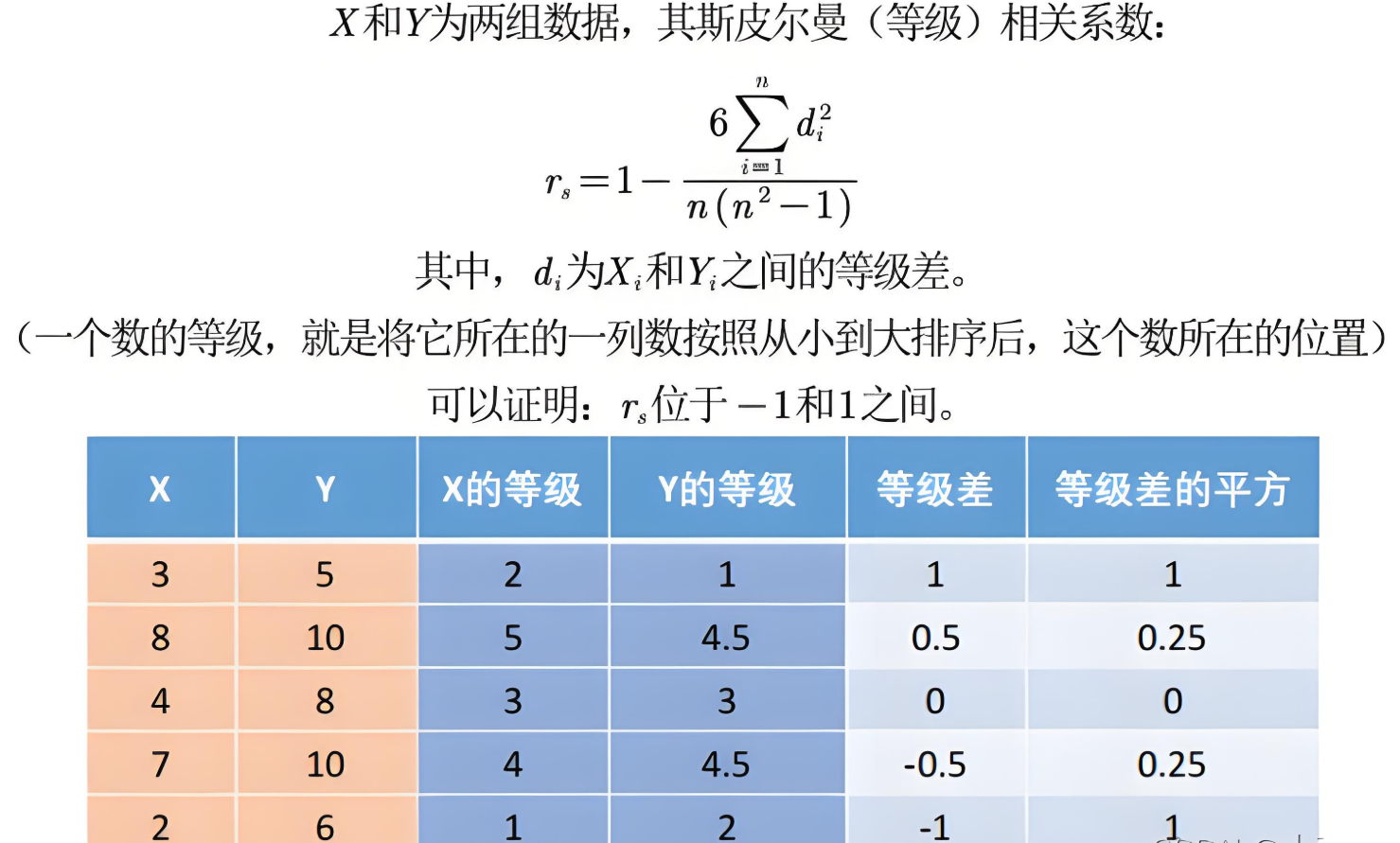
所谓“秩”（Rank），通俗地说就是对原始观测数据进行排序之后所得到的“名次”或“位置号”。例如，一个数据集 {15, 8, 23} 按升序排列后为 {8, 15, 23}，则对应的秩分别为 {1, 2, 3}。Spearman相关系数就是以这些秩为基础来计算相关性的统计量。在实际操作中，对于两个变量 \(X\) 与 \(Y\)，我们首先分别对各自的观测值进行升序排序，分配秩值 \(r(x_i)\)、\(r(y_i)\)，然后用皮尔逊相关系数的公式对秩进行相关分析。换句话说，Spearman相关系数其实是“变量秩之间的Pearson相关系数”，其定义为：

\[\rho_s = \frac{\text{cov}(r(X), r(Y))}{\sigma_{r(X)} \sigma_{r(Y)}} \]

其中 \(r(X), r(Y)\) 分别表示变量 \(X\) 与 \(Y\) 中每个观测值对应的秩，\(\text{cov}\) 表示协方差，\(\sigma\) 表示标准差。

当不存在秩重复（即数据中没有重复值）时，Spearman相关系数还有一个更简洁的公式：

\[\rho_s = 1 - \frac{6 \sum d_i^2}{n(n^2 - 1)} \]

其中 \(d_i = r(x_i) - r(y_i)\) 表示第 \(i\) 个观测值在两个变量中的秩差，\(n\) 为观测样本量。

该公式有如下几个直观解释：

  • 若两个变量排名完全一致，即所有 \(d_i = 0\)，则 \(\rho_s = 1\)，表示完全正相关。
  • 若两个变量排名完全相反，即 \(d_i = n - i - i = n - 2i\)（或其它等效形式），则 \(\rho_s = -1\)，表示完全负相关。
  • 若排名无规则对应，则 \(\rho_s\) 可能接近于0，表示无相关性。

值得强调的是，与皮尔逊相关系数主要度量线性关系不同，Spearman相关系数度量的是单调关系。也就是说，只要变量之间是单调递增或递减的，哪怕曲线是非线性的（如指数型、对数型等），Spearman系数也能正确反映其高度相关性。这一点使得Spearman方法在实际中具有更强的适应性和鲁棒性。此外，由于秩的定义不依赖于变量的分布形态，因此Spearman相关系数属于非参数统计方法（non-parametric methods），对正态分布的要求较低，特别适用于分布未知或分布偏态的数据场景。正因如此，它在数据科学实践中与Kendall秩相关系数一起，成为分析非线性相关的重要工具。

二、Spearman秩相关的性质与适用条件

Spearman秩相关系数因其非参数性质和对数据分布的宽容性，在各种应用场景中都表现出显著优势。以下表格总结了该统计量的关键特性及其适用条件，并在后文进行详细阐述：

特性 说明
非参数性 不要求变量服从正态分布
单调性 可以捕捉单调但非线性关系
抗极端值能力强 对离群值不敏感
适用于顺序变量 可处理等级、序数数据
不适合测量非单调关系 对非单调变换的关系不敏感
  • 非参数性。Spearman系数是典型的非参数统计方法。在使用Pearson系数进行分析时，通常要求数据满足线性关系、连续型变量以及接近正态分布。而Spearman方法则无需这些前提条件，它只依赖于秩的排列，不对变量的具体分布作出假设，因此更适合处理非正态、偏态甚至含有异常值的数据集。
  • 单调性。Spearman相关系数主要度量变量之间是否存在单调关系。所谓单调，即一个变量增加时另一个变量总是（或大体上）增加或减少。无论该关系是线性、对数型还是指数型，只要保持单调性，Spearman系数都能有效识别并量化这种趋势。这种特性使其优于Pearson系数在分析非线性但单调关系的数据时更具解释力。
  • 抗极端值能力强。由于Spearman是基于秩的统计量，极端值对其影响非常有限。例如，某个样本点的观测值再极端，其在排序中的秩值仍然处于合理范围内，不会像Pearson那样拉高协方差和标准差，从而显著扭曲结果。因此，Spearman在数据中包含离群点（outliers）时仍能保持稳健性。
  • 适用于顺序变量。Spearman特别适合处理顺序变量（Ordinal Variables），如满意度等级（非常满意、满意、不满意）、学业等级（优、良、中、差）等。这些变量通常不能进行加减乘除等数值操作，但可以进行大小比较和排序。Spearman通过计算秩之间的相关性，自然适应了这类变量的特点。
  • 对非单调关系不敏感。值得注意的是，尽管Spearman优于Pearson在识别单调非线性关系方面的表现，但它对**非单调关系（如抛物线型或U型关系）**的识别能力较弱。如果两个变量呈现非单调但高度依赖的关系，Spearman相关系数可能会接近0，误导为“无相关”，这时需要配合其他方法（如距离相关系数、核相关分析等）进行补充判断。

三、Spearman 秩相关系数计算过程

3.1 原始数据表

序号 1 2 3 4 5 6 7 8 9 10
MMI 220 218 216 217 215 213 219 236 237 235
S&P100 151 150 148 149 147 146 152 165 162 161

3.2 秩赋值、秩差与平方差

秩排名规则：最小值秩为1，最大值秩为10

序号 1 2 3 4 5 6 7 8 9 10
MMI 220 218 216 217 215 213 219 236 237 235
Rank(MMI) 7 5 3 4 2 1 6 9 10 8
S&P100 151 150 148 149 147 146 152 165 162 161
Rank(S&P100) 6 5 3 4 2 1 7 10 9 8
\(d_i\) 1 0 0 0 0 0 -1 -1 1 0
\(d_i^2\) 1 0 0 0 0 0 1 1 1 0

秩差平方和：

\[\sum d_i^2 = 1 + 0 + 0 + 0 + 0 + 0 + 1 + 1 + 1 + 0 = 4 \]

3.3 Spearman 秩相关系数计算公式

公式如下：

\[\rho = 1 - \frac{6 \sum d_i^2}{n(n^2 - 1)} \]

其中，

  • $n = 10 $（样本个数）
  • $ \sum d_i^2 = 4 $

代入公式：

\[\rho = 1 - \frac{6 \times 4}{10(10^2 - 1)} = 1 - \frac{24}{990} = 1 - 0.02424 = 0.9758 \]

说明它们之间存在极强的正相关性（接近于1）。

四、Python与R实现Spearman相关系数

4.1 Python实现（pandas + scipy）

import pandas as pd
from scipy.stats import spearmanr

# 示例数据
x = [106, 86, 100, 101, 99]
y = [7, 0, 27, 50, 28]

# 计算 Spearman 相关系数
corr, p_value = spearmanr(x, y)
print(f"Spearman相关系数：{corr:.3f}，p值：{p_value:.4f}")

4.2 R语言实现

x <- c(106, 86, 100, 101, 99)
y <- c(7, 0, 27, 50, 28)

# spearman方法
cor.test(x, y, method = "spearman")

4.3 单调但非线性关系图

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(1, 100, 100)
y = np.log(x)

plt.scatter(x, y)
plt.title("单调但非线性关系")
plt.xlabel("X")
plt.ylabel("Y")
plt.grid(True)
plt.show()

4.4 热力图展示相关矩阵

import seaborn as sns
import pandas as pd
import numpy as np 
import matplotlib.pyplot as plt

# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 示例数据
df = pd.DataFrame({
    'X1': np.random.rand(100),
    'X2': np.random.rand(100),
    'X3': np.random.rand(100)
})

# 计算 Spearman 矩阵
corr_matrix = df.corr(method='spearman')

sns.heatmap(corr_matrix, annot=True, cmap="coolwarm")
plt.title("Spearman相关热力图")
plt.show()

五、Spearman相关系数的统计推断与假设检验

在实际数据分析中，仅计算Spearman相关系数的数值并不足以说明变量之间是否具有显著的秩相关关系。为了判断这种关系是否具有统计学意义，我们需要进行假设检验。这一过程包括构造假设、计算统计量、获取p值并做出结论判断。

5.1 假设检验

我们通常通过如下假设来检验两个变量之间是否存在秩相关关系：

  • 零假设 H₀：变量之间不存在Spearman秩相关关系，即 $$\rho_s$ = 0；
  • 备择假设 H₁：变量之间存在显著的Spearman秩相关关系，即 $$\rho_s$ ≠ 0。

换句话说，零假设认为观测到的秩相关是由于随机性造成的，而备择假设认为存在真实的单调关系。如果在一定显著性水平（例如α = 0.05）下观察到的p值小于α，则拒绝零假设，说明变量之间的秩相关是统计显著的。

5.2 p值计算与检验方法

在Python中，借助SciPy库的 scipy.stats.spearmanr() 函数，可以方便地同时获得Spearman相关系数和其对应的p值：

from scipy.stats import spearmanr

x = [12, 15, 14, 10, 9]
y = [100, 115, 120, 90, 80]
corr, p_value = spearmanr(x, y)
print(f"Spearman相关系数: {corr:.4f}, p值: {p_value:.4f}")

如果p值小于显著性水平（通常设定为0.05），则可以拒绝零假设，认为两个变量之间的秩相关关系在统计学上是显著的。值得注意的是，p值的大小不仅取决于相关系数的绝对值，还与样本容量有关。在小样本数据中，即使相关系数较大，p值也可能不显著。

5.3 样本量与精度

在大样本（n > 30）条件下，Spearman相关系数的抽样分布近似服从正态分布，此时可以用z检验方法进一步推导置信区间或进行双侧检验。而在小样本情形下（n ≤ 30），通常会查表获得精确的临界值或使用置换检验法估计p值，这种方法更稳健，尤其适用于非标准分布和离群值较多的情况。

总结

Spearman秩相关系数是一种基于秩的非参数统计方法，适用于衡量两个变量之间的单调关系，无论该关系是否线性。它通过将原始数据转换为秩，再计算这些秩之间的Pearson相关，从而避免了对数据分布的强假设。由于对极端值不敏感、适用于顺序变量，Spearman在心理学、教育、社会科学等领域得到广泛应用。在统计推断方面，可以通过假设检验判断秩相关是否显著，常用的方法是基于p值的显著性检验。当使用如Python的 scipy.stats.spearmanr() 函数时，能同时返回相关系数和p值，为数据分析提供便捷的工具。总体而言，Spearman相关系数是一种稳健、直观且应用灵活的相关性分析工具。

作者：ChatGPT
发布日期：2025年5月
标签：Spearman相关系数，非参数统计，秩相关，Python实现

posted @ 2025-05-21 23:03  郝hai  阅读(1509)  评论(0)    收藏  举报