讨价还价博弈(Bargaining)——从Rubinstein模型到现实谈判策略

在现实经济与国际关系中，博弈各方常常就资源分配或协议条款展开谈判，这类情境被称为“讨价还价博弈”。与一般静态博弈不同，讨价还价博弈强调谈判过程的动态性和时序性，即参与者轮流提出报价，并决定是否接受对方的提议或继续协商。该类博弈广泛存在于劳资谈判、商业合同制定、国际贸易协议等场景中，尤其在合作性较强但利益分配存在分歧的博弈关系中更为典型。
讨价还价博弈的关键在于时间偏好、议价能力和先手优势。各方在考量未来收益折现价值的基础上，决定是尽早接受次优条件还是等待更优提议，从而展现出策略上的理性权衡。这一博弈框架不仅能刻画谈判行为的基本逻辑，也为理解谈判结果的稳定性与公平性提供了系统的理论支持。特别是在不完全信息或持续互动的背景下，讨价还价博弈为现实谈判分析提供了深刻启示。

一、引言

讨价还价是人类社会中最具普遍性的交互行为之一。无论是在菜市场买菜、房地产交易中商定价格，还是跨国公司之间签署战略协议，讨价还价始终作为达成一致意见的重要手段存在。在经济学与博弈论的语境下，讨价还价（Bargaining）被抽象为双方或多方对资源进行分配的动态过程，每一方都试图在不撕破合作前提的前提下，最大化自身利益。
与传统的价格理论或拍卖理论不同，讨价还价的特征在于：它强调的是协议的过程，而非市场所决定的价格结果。在这个过程中，玩家间的行为策略、信息结构、耐心程度、时间偏好等因素都会对结果产生关键影响。博弈论，尤其是非合作博弈模型，为我们提供了一种系统化的工具，以研究这类策略性交互。讨价还价主要可以分为两大类模型：一是静态讨价还价模型，以纳什（John Nash）提出的“纳什讨价还价解”最为经典，它关注的是一锤定音式的协商过程；二是动态讨价还价模型，最具代表性的则是Rubinstein在1982年提出的无限期轮流出价模型，它揭示了“时间偏好”对分配结果的深刻影响。随着现实问题的复杂性增加，研究者们也发展出不完全信息讨价还价、有限轮次模型、多方协商模型等多个变体，尝试更贴近真实谈判环境。例如，在一项国际协定谈判中，参与国对协议的“底线”并不透明，各自的政治耐心和公众压力也有所不同，这些都呼唤更复杂、更精准的模型进行分析。

二、静态讨价还价模型（Nash Bargaining）

2.1 模型背景与定义

纳什讨价还价模型是一种经典的静态博弈模型，用来刻画两个理性个体如何就某种“合作性收益”进行协商分配。在这个模型中，协商不是一个过程，而是一锤定音的“协商结果”：若谈判成功，资源依某种比例分配；若失败，则双方都得到一个保留值（disagreement point）。形式化地设定如下：

• 有两个玩家，记为 \(i=1,2\)；
• 所有可行的分配方案构成一个集合 $S \subseteq \mathbb{R}^2$，其中 \((x_1,x_2)\in S\) 表示一种资源分配方式；
• 双方若未达成协议，各自的保留值为 \(d = (d_1,d_2)\)，其中 $d \in S$，且代表不合作时的收益；
• 玩家目标是选择 \((x_1,x_2)\in S\)，使得两人都“尽可能优于保留点”。

2.2 纳什讨价还价解的公理化推导

纳什在1950年提出了一组对理性讨价还价解决方案应满足的公理，并基于这些公理唯一确定了解的形式。这四个公理是：

• 有效性（Pareto Efficiency）：所选解在可行集合 \(S\) 中是帕累托最优的；
• 对称性（Symmetry）：若 $S$ 关于两玩家对称且 \(d_1 = d_2\)，则解也应对称；
• 独立于无关备选项（IIA）：若从 \(S\) 中删除与当前解无关的劣质选项，解不应改变；
• 缩放不变性（Invariance to affine transformations）：单位变换或加常数不应影响解决方案的相对结构。

纳什证明，满足以上四个公理的唯一解是：

\[\arg\max_{(x_1,x_2) \in S, x_i \ge d_i} (x_1 - d_1)(x_2 - d_2) \]

即，在所有优于保留点的分配中，最大化双方“净收益乘积”。这个乘积被称为“纳什积”。

2.3 图形化解释

为了帮助理解，我们以一个具体例子说明：
设可行集合 \(S\) 为二维平面上一个凸集，保留点为 \(d = (0,0)\)，即双方谈崩时一无所得。若 \(S\) 是一个包含 \((0,0),(1,0),(0,1),(0.5,0.5)\) 等点的凸集合，我们可以画出 \(S\) 的边界，并在图中找到使 \((x_1 \cdot x_2)\) 最大的那个点，即是纳什解。在Python中我们可以利用如下代码画出此图形（使用matplotlib）：

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize

# 可行集合 S 中的边界点
points = np.array([[0, 0], [1, 0], [0, 1], [0.5, 0.5]])

# 目标函数（负纳什积）
def nash_product(x):
    return -(x[0]) * (x[1])

# 约束条件：在凸包中，且 x,y ≥ 0
constraints = ({'type': 'ineq', 'fun': lambda x: x[0]},
               {'type': 'ineq', 'fun': lambda x: x[1]},
               {'type': 'ineq', 'fun': lambda x: 1 - x[0] - x[1]})

res = minimize(nash_product, [0.3, 0.3], constraints=constraints)

plt.figure(figsize=(6,6))
plt.plot([0,1,0],[0,0,1],'k--')
plt.fill([0,1,0.5,0],[0,0,0.5,1], color='lightgrey', alpha=0.6)
plt.plot(res.x[0], res.x[1], 'ro', label='Nash Solution')
plt.xlabel('Player 1 Utility')
plt.ylabel('Player 2 Utility')
plt.legend()
plt.title('Nash Bargaining Solution')
plt.grid(True)
plt.show()

纳什讨价还价模型虽然简单，但它提供了一个重要的“谈判公平性”标准。通过最大化“合作净收益乘积”，它既考虑到效率，也考虑到平衡——如果一方保留值更高，解自然更偏向他。然而，这个模型仍存在一个限制：它忽略了“谈判过程”，即时间因素和出价顺序未被建模。这也正是下一节Rubinstein模型试图解决的问题。

三、动态讨价还价模型：Rubinstein 模型

3.1 模型背景

在经典的讨价还价理论中，Rubinstein（1982）模型是一种基础而强有力的形式化工具，用于描述两个玩家在无外部干预下如何轮流提出报价，并最终就资源分配达成一致。该模型的核心特征包括：

• 无限轮谈判假设：即谈判过程可能无穷延续下去，直到某一方接受报价；
• 轮流报价机制（Alternating Offers）：两个谈判方交替提出资源分配方案；
• 时间与耐心的重要性：通过引入折现因子 \(\delta\)（\(0 < \delta < 1\)），模型赋予耐心者更大的议价优势，折现因子越大，表明谈判方越“耐心”，对未来的收益越看重；
• 无外部强制终止条件：即谈判只在一方接受报价后才结束。

该模型最适用于描述劳资谈判、国际协议、贸易协定等情形，特别是在参与方有动力进行持续协商、但又存在时间成本或机会成本的场景中。

3.2 模型定义

Rubinstein 模型构建在以下假设基础上：

• 玩家：两个玩家 \(P_1\) 和 \(P_2\)；
• 折现因子：
  • 玩家 \(P_1\) 的折现因子为 \(\delta_1\)；
  • 玩家 \(P_2\) 的折现因子为 \(\delta_2\)；
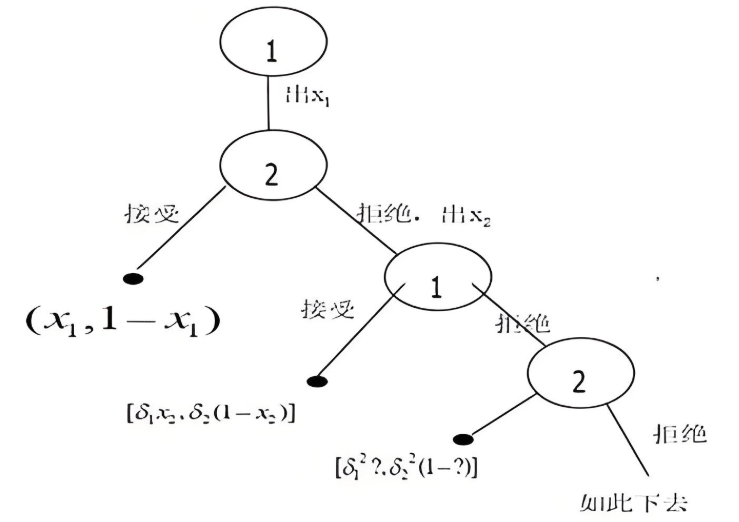
• 提议轮规则：
  • 第 1 轮由 \(P_1\) 提出资源分配方案 \((x, 1 - x)\)；
  • \(P_2\) 决定是否接受；
  • 如果拒绝，则进入第 2 轮，由 \(P_2\) 提议 \((y, 1 - y)\)，\(P_1\) 决定是否接受；
  • 依此类推；
• 效用函数：
  • 玩家 \(P_1\) 在 \(t\) 轮接受方案 \((x_t, 1 - x_t)\)，其效用为 \(\delta_1^t x_t\)；
  • 玩家 \(P_2\) 在 \(t\) 轮接受方案，其效用为 \(\delta_2^t (1 - x_t)\)。

目标是求解该博弈的子博弈精炼纳什均衡（Subgame Perfect Nash Equilibrium, SPNE）。

3.3 均衡求解（Subgame Perfect Equilibrium）

Rubinstein 使用逆向归纳法求解此模型的均衡。在无限轮下，均衡策略为：一方提出一个令对方刚好接受的分配值，从而在第一轮即达成协议。

均衡解公式如下：

• 玩家 \(P_1\) 在第 1 轮提出的最优方案为：
  \[x^* = \frac{1 - \delta_2}{1 - \delta_1 \delta_2} \quad \quad y^* = \frac{\delta_1 (1 - \delta_2)}{1 - \delta_1 \delta_2} \]

其中：

• \(x^*\) 表示 \(P_1\) 在第一轮的效用；
• \(y^*\) 表示 \(P_2\) 在第二轮轮到他出价时的效用（即 \(P_1\) 接受的份额）；
• 为确保 \(P_2\) 接受 \(P_1\) 的报价，\(P_1\) 给出的份额必须等于或大于 \(P_2\) 在下一轮的折现期望。

经济直觉：

• 更有耐心的一方获得更多份额；
• 如果 \(\delta_1 > \delta_2\)，说明 \(P_1\) 更耐心，则其在均衡中获得更多资源；
• 当 \(\delta_1 = \delta_2\) 时，双方平分资源，\(x^* = y^* = 0.5\)；
• 若某一方极不耐心（如 \(\delta_2 \rightarrow 0\)），其在谈判中几乎得不到任何份额。

3.4 代码实现（Python）

以下 Python 代码实现 Rubinstein 模型的均衡解计算，并绘制出不同折现因子对最终议价结果的影响图。

import numpy as np
import matplotlib.pyplot as plt

def rubinstein_equilibrium(delta1, delta2):
    """
    计算 Rubinstein 动态讨价还价模型的均衡解
    参数：
        delta1: 玩家1的折现因子
        delta2: 玩家2的折现因子
    返回：
        x_star: 玩家1在第一轮提出的最优分配份额
        y_star: 玩家2在第二轮提出时的最优分配份额
    """
    if not (0 < delta1 < 1 and 0 < delta2 < 1):
        raise ValueError("折现因子必须在 (0,1) 之间")
    
    x_star = (1 - delta2) / (1 - delta1 * delta2)
    y_star = delta1 * (1 - delta2) / (1 - delta1 * delta2)
    return round(x_star, 4), round(y_star, 4)

def plot_equilibrium_vs_delta1(delta2_fixed=0.9):
    """
    绘制 delta1 不同取值下，Rubinstein 模型均衡分配的变化
    """
    delta1_vals = np.linspace(0.01, 0.99, 200)
    x_stars = []
    y_stars = []

    for delta1 in delta1_vals:
        x, y = rubinstein_equilibrium(delta1, delta2_fixed)
        x_stars.append(x)
        y_stars.append(y)

    plt.figure(figsize=(10, 6))
    plt.plot(delta1_vals, x_stars, label="x* (Player 1's Share)", color='blue')
    plt.plot(delta1_vals, y_stars, label="y* (Player 2's Value)", color='green')
    plt.axvline(x=delta2_fixed, linestyle='--', color='gray', label=f'delta2 = {delta2_fixed}')
    plt.xlabel("delta1 (Player 1's Patience)")
    plt.ylabel("Equilibrium Share")
    plt.title("Rubinstein Bargaining Equilibrium vs Player 1's Patience")
    plt.legend()
    plt.grid(True)
    plt.tight_layout()
    plt.show()

def user_interactive():
    """
    用户输入折现因子，输出均衡解
    """
    print("Rubinstein 模型均衡解计算器")
    try:
        delta1 = float(input("请输入玩家1的折现因子 delta1（0-1之间）："))
        delta2 = float(input("请输入玩家2的折现因子 delta2（0-1之间）："))
        x_star, y_star = rubinstein_equilibrium(delta1, delta2)
        print(f"\n结果：")
        print(f"玩家1第一轮应提出的分配份额 x* = {x_star}")
        print(f"玩家2在下一轮预期获得的份额 y* = {y_star}")
    except Exception as e:
        print("发生错误：", e)

if __name__ == "__main__":
    # 示例运行
    user_interactive()

    # 可视化影响图（固定 delta2 = 0.9）
    plot_equilibrium_vs_delta1(delta2_fixed=0.9)

四、有限轮讨价还价模型分析

在现实世界中，许多谈判并不是无限轮博弈，而是必须在有限时间内完成。例如，劳资谈判、国际贸易协议、合同协商等，通常都有明确的截止期限。一旦期限到达仍未达成协议，则可能导致谈判失败或出现强制仲裁。为此，经济学家在Rubinstein（1982）无限轮讨价还价模型的基础上，引入了有限轮谈判模型，更贴近现实情况。

4.1 模型设定

我们设定一个最多进行 \(T\) 轮的有限轮讨价还价博弈，其核心假设如下：

• 有两位玩家，\(A\) 与 \(B\)，轮流提出如何分配总价值 1 的出价；
• 谈判总共可以进行 \(T\) 轮（\(T\) 为奇数或偶数）；
• 若 \(T\) 为偶数，则 \(A\) 在第 0、2、…轮出价；若 \(T\) 为奇数，\(A\) 仍先手；
• 每一轮被出价者可以选择接受或拒绝；
• 若接受，游戏结束，按照当前出价分配；
• 若最后一轮仍未达成协议，则由出价者提出“最后通牒”；
• 每位玩家均有贴现因子 \(\delta_A, \delta_B \in (0, 1)\)，反映他们的时间偏好。

该模型的核心特征在于：随着谈判接近最后一轮，参与者的策略将显著变化，出价将趋于强制性、压迫性，博弈结构更像“最后通牒博弈”。

4.2 倒推法求解过程

该模型最合适的求解方式是逆向归纳法（backward induction）。我们通过一个 \(T=3\) 的例子来说明过程，假设 \(A\) 先手：

第三轮（\(t=2\)）

此轮为最后一轮，由 \(A\) 出价：

• \(A\) 知道：若 \(B\) 拒绝，则双方得零；
• 因此 \(A\) 只需提出 \((1 - \varepsilon, \varepsilon)\)，其中 \(\varepsilon > 0\) 足够小；
• \(B\) 会接受任何正收益；
• \(A\) 实得近似 \(1\) 的收益，折现值为 \(\delta_A^2\)。

第二轮（\(t=1\)）

此轮轮到 \(B\) 出价：

• \(B\) 预期若 \(A\) 拒绝，他将在第三轮接受 \((1 - \varepsilon, \varepsilon)\)；
• 所以 \(A\) 的预期收益为 \(\delta_A^2 (1 - \varepsilon)\)；
• 为使 \(A\) 接受，\(B\) 需给其至少 \(\delta_A^2\)；
• 因此 \(B\) 最优出价为 \((\delta_A^2, 1 - \delta_A^2)\)；
• \(B\) 实得收益为：\(\delta_B (1 - \delta_A^2)\)。

第一轮（\(t=0\)）

\(A\) 回顾整个过程：

• 若 \(B\) 拒绝，下一轮 \(B\) 会出价 \((\delta_A^2, 1 - \delta_A^2)\)；
• \(B\) 的预期折现收益为 \(\delta_B (1 - \delta_A^2)\)；
• 为使 \(B\) 接受，\(A\) 应给其至少这一数额；
• 所以 \(A\) 出价为 \((1 - \delta_B (1 - \delta_A^2), \delta_B (1 - \delta_A^2))\)；
• \(B\) 会接受，因为其比下一轮更有利。

最终结果为：第一轮就达成协议，出价人为先手的 \(A\)，得到了明显优势。

4.3 一般形式解

在一般的有限轮数 \(T\) 中，解决该模型依然适用逆向归纳：

• 最后一轮是“最后通牒博弈”；
• 向前逐轮推导，每轮的提议都基于下一轮对手的预期收益；
• 每一轮的均衡出价都涉及贴现因子的复合形式，结构复杂但有规律；
• 越早的出价方越有议价权，越接近终点议价能力越弱。

Rubinstein（1982）进一步证明，在 \(\delta_A = \delta_B = \delta\) 时，先手优势更明显；若 \(\delta_A < \delta_B\)，则时间耐心较强者更有议价权。

4.4 模型意义与政策启示

该模型有着广泛的现实意义和政策参考价值：

• 现实性增强：许多谈判场景都有限制期限，如劳资谈判、财政预算、国际协议等；
• 谈判节奏控制：掌握谈判进度是一种策略，先手者可故意拖延，以迫使对手让步；
• “最后通牒效应”：最后一轮强制出价的设置，在现实中体现为法律仲裁、裁判决定等机制；
• 设定时间边界：合理设置谈判的截止时间，有助于打破谈判僵局，激励各方尽快妥协；
• 时间偏好策略：通过塑造自身的“低贴现率”形象（如“我不急”），可获得更好的议价结果；
• 战略预期管理：掌握对手的贴现因子和预期，是制定最优出价的关键。

简而言之，有限轮讨价还价模型不仅为谈判提供了一个精确的分析工具，更强调了时间、顺序与耐心在博弈中的决定性作用。

五、现实博弈中的策略思维与模型应用

Rubinstein 模型及其各类扩展版本不仅在理论经济学中具有里程碑意义，更广泛应用于现实世界中的谈判、市场行为、政策博弈等领域。从劳资冲突到国际贸易、从企业并购到数字平台博弈，均可见其深刻影响。

5.1 劳资谈判中的讨价还价

在劳资关系中，工会（Union）与企业资方（Firm）常围绕工资水平、工作时间、待遇等问题展开讨价还价。Rubinstein模型中的贴现因子 \(\delta\)，恰可代表工会的耐心程度或资方复工的紧迫程度。

• 工会越“耐心”（即 \(\delta\) 越高），其在谈判中坚持高工资要求的能力越强；
• 若资方越急于恢复生产（贴现率低），则在谈判中让步越多；
• 罢工本质上是一种提升自身贴现因子的策略，通过延长博弈时间来对资方施压。

这种“拖延施压”行为是博弈论中耐心战略的现实体现。

5.2 国际贸易谈判中的战略地位

在 WTO 协议、自由贸易协定（FTA）等多边或双边贸易谈判中，各国围绕关税、市场准入展开博弈。Rubinstein 模型揭示：

• 谈判具有明确时间窗口，具有有限轮博弈特征；
• 强势国家（如发达国家）通常具有更高贴现因子 \(\delta\)，因此表现出更强耐心；
• 发展中国家由于急于达成协议（贴现率低），常被迫在谈判中做出更多让步；
• 通过组成联盟（如金砖国家、非盟）增强整体议价权，是对抗时间压力和贴现劣势的策略之一。

5.3 企业并购（M&A）与出价策略

企业收购常构成一个有限轮的出价博弈，符合Rubinstein框架。并购博弈中的策略包括：

• 出价方（通常为大公司）处于主动出价地位；
• 被收购企业若存在资金压力或股东急需变现，其贴现因子低，容易被压价；
• 因此，被收购方可通过制造时间耐心假象（如引入多方竞购者）提高议价空间；
• 投资银行会设计分阶段的报价方案、设置“锁定期”等，以优化出价节奏。

这种节奏控制正体现了对博弈时间结构的精细运用。

5.4 数字平台算法中的自动化谈判

在淘宝、亚马逊等电商平台中，平台与商户之间的佣金、流量分配等常通过博弈达成协议。Rubinstein模型启示我们：

• 平台为“先手”一方，具备制度与时间优势；
• 商户分散、谈判地位弱，更容易接受平台规则；
• 通过设定倒计时优惠、限时报价等方式，平台人为制造有限轮博弈压力；
• 基于模型设计自动谈判代理人（Negotiation Agent），已广泛应用于价格谈判、服务推荐等算法经济系统中。

5.5 AI策略博弈与博弈图建模

在AI与博弈论结合的研究领域中，Rubinstein模型也可转化为决策树结构，用于训练智能体进行策略学习：

• 可用于训练强化学习代理人预测对手反应，实现最优策略；
• 在PPO（Proximal Policy Optimization）等算法下构建谈判学习环境；
• 被广泛用于金融AI交易、自动竞标系统、法律博弈模拟等高维策略空间中；
• 通过“有限轮+贴现率+博弈树”的组合结构，为AI带来了更现实的谈判学习框架。

六、Rubinstein模型的数学拓展与现代演化

Rubinstein（1982）模型通过轮流出价博弈形式，揭示了贴现因子对讨价还价结果的关键影响，为非合作博弈下的谈判建模奠定基础。其广泛适用于劳资协商、企业并购、国际谈判、数字平台等领域，并被不断拓展，以更贴近现实博弈情境。

有限轮讨价还价模型
现实中谈判常有时限，有限轮模型设定总轮数为 \(T\)，若期满未达成协议即破裂。通过逆向归纳法求解可得均衡策略，体现出明显的“最后一轮优势”。相比无限期模型，后手方更具策略空间，结果更贴近现实节奏。
不完全信息下的议价
在多数博弈中，玩家的贴现因子为私人信息，使谈判具有信号博弈特征。该类模型纳入信念更新与Bayes最优反应，均衡形式为Perfect Bayesian Equilibrium，强调信息不对称对议价效率与结果的影响。
多人讨价还价模型
Baron-Ferejohn模型扩展Rubinstein框架至多方议价，设定轮流提案并通过投票机制决定协议达成。权力分配、议程设置等成为影响收益的重要变量，也推动合作博弈与非合作理论的交叉融合。
动态契约与自执行机制
现实协议常伴随后续执行风险，动态博弈理论如Abreu等提出的自执行契约模型强调以未来惩罚确保当前承诺的可信性，促成了讨价还价模型与动态合约理论的融合。
理论贡献与未来前沿
Rubinstein模型通过精确博弈结构建模，为非合作视角下的谈判提供微观基础，解释了Nash谈判解的极限形式。未来研究可从三方向深化：
（1）行为博弈拓展：引入锚定、损失厌恶等非理性因素；
（2）机制设计创新：优化报价顺序、表决规则等制度安排；
（3）AI与算法议价：发展可学习的策略Agent，模拟复杂多智能体谈判行为。

总结与展望

在当前中美贸易摩擦的背景下，Rubinstein讨价还价模型展现出强烈的现实意义。该模型通过动态轮流出价博弈，揭示了贴现因子与时间偏好对谈判结果的决定性影响。在中美关税争端中，双方轮番加征关税、设置反制措施，实质构成多轮讨价还价过程。美国频繁主动出招，试图利用“先动优势”主导谈判节奏；而中国则通过延迟回应与市场多元化策略，展现出更强的时间耐受力。Rubinstein模型指出，贴现因子越大（越有耐心）的一方将获得更有利结果，这为我们理解“以拖促稳”策略的有效性提供了理论支撑。
作为现代讨价还价理论的基础，Rubinstein模型不仅连接了非合作与合作解，还在有限轮次、不完全信息与多方博弈等方面得到拓展，极大地丰富了谈判理论体系。未来研究可从三方面深化：一是引入行为经济学因素，更真实地还原人类决策行为；二是结合机制设计优化议价流程；三是推动AI环境下的算法化谈判策略建模。随着技术发展与国际博弈复杂化，该模型将在理论与实践中持续发挥核心作用。

参考文献

Rubinstein, A. (1982). "Perfect Equilibrium in a Bargaining Model", Econometrica, 50(1), 97–109.
Binmore, K., Rubinstein, A., & Wolinsky, A. (1986). "The Nash Bargaining Solution in Economic Modelling", RAND Journal of Economics, 17(2), 176–188.
Osborne, M. J., & Rubinstein, A. (1990). Bargaining and Markets, Academic Press.
Abreu, D., Pearce, D., & Stacchetti, E. (1990). "Toward a Theory of Discounted Repeated Games with Imperfect Monitoring", Econometrica, 58(5), 1041–1063.