统计学(二十五)——统计指数概要
在现实生活与经济社会活动中,各类现象的数量变化错综复杂,既包括单一现象随时间或地区的变动,也包含多个不同现象综合变动的情况。特别是在价格、产量、收入、成本、物价等经济现象中,单纯依靠原始数据很难全面、直观地反映总体变动的趋势与程度。统计指数便应运而生,统计指数是一种通过对比不同时间、地区或条件下多个相关指标变动情况的相对数,来综合反映复杂现象总体数量变动方向与程度的分析方法。它不仅能够帮助我们揭示经济现象变动背后的结构性特征,还能为决策分析、政策调整、趋势判断提供重要依据,是现代统计分析中应用极其广泛的重要工具。
📖 一、统计指数概述
统计指数是一种反映经济现象数量变动状况的相对数,根据对象性质和复杂程度,分为广义和狭义两类。
-
广义:描述简单总体数量【数量可直接相加减的现象总体,如人数、播种面积】变动状况的相对数,直接反映可加减经济现象数量随时间、地区、条件等的变化。
例子:武汉大学学生人数逐年变动、农作物播种面积逐年变化。 -
狭义:描述复杂总体数量【数量不可直接相加减的现象总体,由不同类别、单位、性质的经济现象构成,如多个商品销售收入】变动状况的相对数,通常涉及多种经济现象或多项标志综合后的变化情况。
例子:超市多种商品综合销售量的年变动情况。
1.1 统计指数作用
统计指数的作用主要体现在以下四个方面:
📌 综合反映复杂现象总体数量变动的方向与程度
- 当计算结果大于100%,说明总体数量上升;小于100%,说明总体数量下降。
- 与100%的偏差表示变动程度,正数为上升幅度,负数为下降幅度。
📌 分析各因素变动对总体变动的影响方向与程度
- 例子:
- 销售额变动 = 销售量指数 × 价格指数
- 总成本变动 = 产量指数 × 单位成本指数
📌 测定现象数量变动受内部各组水平和结构变动的影响
- 通过分解指数体系,定量分析内部不同因素的作用方向和贡献。
📌 研究现象数量长期变动趋势
- 编制连续时间的同类指数序列,观察经济现象长期变化趋势。
📌 综合评价和测定社会经济现象
- 通过指数方法,对多因素、多层次复杂现象进行综合评价与测度。
1.2 统计指数分类
根据不同分类标准,统计指数可分为以下几类:
📌 按对象范围
- 个体指数:反映单一经济现象的变动。
- 总体指数:反映复杂现象总体综合变动。
📌 按现象性质
- 数量指标指数:反映规模数量的变动,如人数、销售量、产量。
- 质量指标指数:反映质量、内涵的变动,如价格、劳动生产率、单位成本。
📌 按比较对象
- 动态指数:反映同一现象随时间变动的指数。
- 静态指数:反映不同地区、不同单位间同一时期现象的比较。
- 计划完成指数:反映计划任务完成程度的指数。
1.3 综合指数的编制原理
综合指数是对两个总量指标对比的相对数,通过固定部分因素,考察另一个因素变动的影响。
📌 特点
-
先综合后对比
- 汇总多项经济现象,形成可比总量。
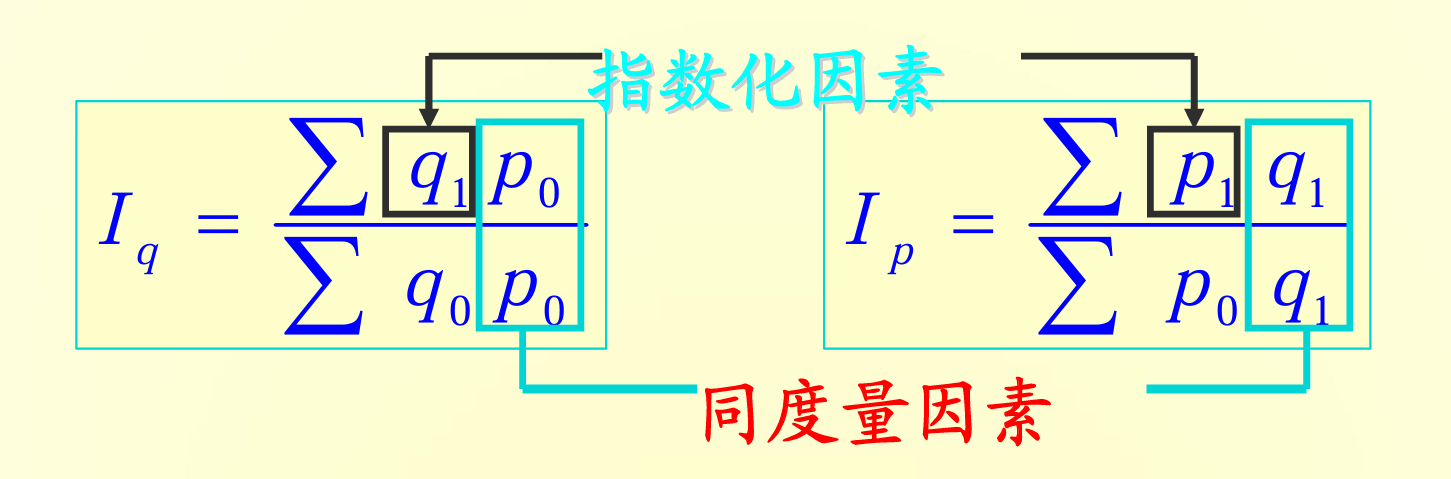
- 引入同度量因素,消除计量单位不同影响。(同度量因素,是指在指数分析中,将多种不同性质或单位的因素,通过统一的度量标准(如金额、数量、重量等)进行转换,使它们具备可加性和可比性,从而便于综合计算和分析各因素对总变动的影响。)
-
固定同度量因素
- 如研究销售量变动 → 固定价格。
- 研究价格变动 → 固定销售量。
-
保证分子、分母范围一致,基于全面资料
- 以相同调查对象、同一时期、相同口径为依据。
📌 编制方法
数量指标指数
- 拉氏(Laspeyres)数量指数\[I_q^L = \frac{\sum q_1 p_0}{\sum q_0 p_0} \]
- 以基期价格为权数,剔除价格变动影响。
- ✅ 剔除价格变动 ❌ 忽视现期实际情况,无法适应新商品。
- 派氏(Paasche)数量指数\[I_q^P = \frac{\sum q_1 p_1}{\sum q_0 p_1} \]
- 以现期价格为权数,反映当前数量变动情况。
- ✅ 反映现状 ❌ 价格变动影响计算结果。
某公司三种商品销售量指数(拉氏数量指数)计算表
| 商品名称 | 计量单位 | 基期 \(q_0\) | 报告期 \(q_1\) | 基期销售价格 \(p_0\)(元) | 基期销售额 \(q_0 p_0\)(元) | 按基期价格计算的销售额 \(q_1 p_0\)(元) |
|---|---|---|---|---|---|---|
| 甲 | 吨 | 160 | 200 | 300 | 48 000 | 60 000 |
| 乙 | 台 | 200 | 210 | 80 | 16 000 | 16 800 |
| 丙 | 米 | 500 | 600 | 20 | 10 000 | 12 000 |
| 合计 | — — | — | — | 74 000 | 88 800 |
计算结果表明:当商品价格固定在基期时,三种商品销售量报告期比基期增加了 20%,由于销售量的综合变动,公司三种商品的销售额报告期比基期增加了 14 800 元。
质量指标指数
- 拉氏价格指数\[I_p^L = \frac{\sum p_1 q_0}{\sum p_0 q_0} \]
- 以基期数量为权数,剔除数量变动影响。
- 派氏价格指数\[I_p^P = \frac{\sum p_1 q_1}{\sum p_0 q_1} \]
- 以现期数量为权数,反映现期价格变动情况。
某公司三种商品价格指数(派氏价格指数)计算表
| 商品名称 | 计量单位 | 基期 \(q_0\) | 报告期 \(q_1\) | 基期销售价格 \(p_0\)(元) | 报告期销售价格 \(p_1\)(元) | 按基期价格计算的销售额 \(q_1 p_0\)(元) | 按报告期价格计算的销售额 \(q_1 p_1\)(元) | 销售额变动额(元) |
|---|---|---|---|---|---|---|---|---|
| 甲 | 吨 | 160 | 200 | 300 | 340 | 60 000 | 68 000 | +8 000 |
| 乙 | 台 | 200 | 210 | 80 | 92 | 16 800 | 19 320 | +2 520 |
| 丙 | 米 | 500 | 600 | 20 | 23 | 12 000 | 13 800 | +1 800 |
| 合计 | — — | — | — | — | — | 88 800 | 101 120 | +12 320 |
计算结果
-
派氏价格指数 \(\bar{K}_p\):
\[\bar{K}_p = \frac{\sum q_1 p_1}{\sum q_1 p_0} = \frac{101 120}{88 800} \approx 114.19\% \] -
销售额变动额:
\[\sum q_1 p_1 - \sum q_1 p_0 = 101 120 - 88 800 = 12 320 \text{元} \]
计算结果说明,该公司商品销售量固定在报告期时,三种商品销售价格总的变动方向是上升的,报告期的价格为基期的 114.19%,报告期的价格比基期的价格上涨了 14.19%。由于商品销售价格总变动的影响,该公司商品销售额增加了 12 320 元。
拉氏指数和派氏指数是统计学中常用的两种指数方法,主要通过固定一个因素,剥离这个因素的影响,衡量另一个因素的变动,用来分析比较价格、数量或价值的变化情况。
拉氏指数以基期的数量或价格作为权重,保持基期结构不变,衡量现期价格或数量的变动情况。它反映在基期条件下,某因素变化对总体变动的影响程度。例如,在基期数量不变的前提下,计算现期价格的变化。
派氏指数则以现期的数量或价格作为权重,固定现期条件,衡量与基期相比,某因素变动的实际影响。它体现的是在现期结构下,某因素变化对总体的作用。
两者的核心思想,都是通过固定一个因素,消除其对总变动的影响,专门考察另一个因素的变动效果。实际应用中,拉氏指数偏重于基期条件,派氏指数更贴近现期情况,常配合使用,用于综合评价经济现象的变动特征和趋势。
📖 二、指数因素分析
2.1 指数体系
指数体系指在数量上存在推算关系的统计指数所构成的整体,其特点有:
- 若干因素指数的乘积等于总变动指数;
- 若干因素对总变动指标的影响之和等于总变动的实际增减额。

(1) 相对数形式:——对象指数等于各个因素指数的连乘积
\[\frac{\sum q_1 p_1}{\sum q_0 p_0} (I_{pq}) = \frac{\sum q_1 p_0}{\sum q_0 p_0} (I_q) \times \frac{\sum q_1 p_1}{\sum q_1 p_0} (I_p) \](2) 绝对数形式:——对象指数的增减额等于各因素指数影响的增减额之和
\[\sum q_1 p_1 - \sum q_0 p_0 = (\sum q_1 p_0 - \sum q_0 p_0) + (\sum q_1 p_1 - \sum q_1 p_0) \]
📌 例1:销售额指数体系
| 指标 | 指数符号 | 计算关系 |
|---|---|---|
| 销售额指数 | \(I_{销售额}\) | \(I_{销售额} = I_{数量} \times I_{价格}\) |
| 销售数量指数 | \(I_{数量}\) | 比较期数量 / 基期数量 |
| 销售价格指数 | \(I_{价格}\) | 比较期单价 / 基期单价 |
👉 特点:
销售额 = 数量 × 单价,因此它们的指数也可以相乘推出总指数。
📌 例 2:企业产值指数体系
| 指标 | 指数符号 | 计算关系 |
|---|---|---|
| 总产值指数 | \(I_{产值}\) | \(I_{产值} = I_{产量} \times I_{单价}\) |
| 产量指数 | \(I_{产量}\) | 比较期产量 / 基期产量 |
| 单价指数 | \(I_{单价}\) | 比较期单价 / 基期单价 |
👉 特点:
产值 = 产量 × 单价,这个指数体系可以分解总产值变动是由数量变动、价格变动还是共同作用导致。
📌 例3:人工成本指数体系
| 指标 | 指数符号 | 计算关系 |
|---|---|---|
| 总工资指数 | \(I_{工资}\) | \(I_{工资} = I_{人数} \times I_{平均工资}\) |
| 从业人数指数 | \(I_{人数}\) | 比较期人数 / 基期人数 |
| 平均工资指数 | \(I_{平均工资}\) | 比较期平均工资 / 基期平均工资 |
👉 特点:
总工资 = 人数 × 平均工资。通过指数体系可以分析:人工成本的上升,是因为员工数量增加,还是工资水平提高,或者二者共同作用。
2.2 因素分析法
因素分析法是根据统计指数体系,从数量方面研究现象总变动中各因素变动的方向、程度和绝对效果的方法。它能够帮助我们明确哪些因素导致了现象的变化,各因素的作用大小如何,便于管理和决策。常见的因素分析法有以下几种:
📌 两因素分析法
当某一总指标受两个因素影响时,分别计算各因素的变动对总变动的影响程度和影响额,是最基础、常用的分析方法。
总量指标变动的两因素分析
销售额 (\(pq\)) = 销售量 (\(q\)) × 单价 (\(q\))
\[\begin{align*} q_0 p_0 &\xrightarrow{q \text{ 变化}} q_1 p_0 \xrightarrow{p \text{ 变化}} q_1 p_1 \\ \frac{\sum q_1 p_1}{\sum q_0 p_0} &= \frac{\sum q_1 p_0}{\sum q_0 p_0} \times \frac{\sum q_1 p_1}{\sum q_1 p_0} = L_q \cdot P_p = I_q \cdot I_p \\ \end{align*} \]
销售额指数 = 销售量指数 × 价格指数
\[\begin{align*} \left\{ \begin{array}{l} \frac{\sum q_1 p_1}{\sum q_0 p_0} = \frac{\sum q_1 p_0}{\sum q_0 p_0} \times \frac{\sum q_1 p_1}{\sum q_1 p_0} \xrightarrow{\text{相对数分析}} \\ \sum q_1 p_1 - \sum q_0 p_0 = (\sum q_1 p_0 - \sum q_0 p_0) + (\sum q_1 p_1 - \sum q_1 p_0) \xrightarrow{\text{绝对数分析}} \end{array} \right. \end{align*} \]
📌 多因素分析法
当总指标同时受到三个及以上因素作用时,需采用多因素分析法,综合分析多种因素对总变动的作用,定量评价各因素的贡献程度。
例4:以创意城本月销售总额较上月增长 20% 为例,可分解为以下两大因素:销售量因素和价格因素,计算如下表:
| 项目 | 指数 | 影响额(元) |
|---|---|---|
| 销售量因素 | 1.10 | +1000 |
| 价格因素 | 1.09 | +900 |
| 总变动 | 1.20 | +1900 |
- 销售量指数 1.10,表示销售数量增长了 10%,贡献了 +1000 元;
- 价格指数 1.09,表示价格上涨了 9%,贡献了 +900 元;
- 总体销售额增长 20%,即 +1900 元。
📌 综合因素分析法
综合因素分析法是指在多因素影响的情况下,先固定某些因素,再分别测算其它因素变动对总变动的影响,最后将各个因素的影响综合起来,求得总变动值。这种方法适用于因素数量较多、因素之间相互影响复杂的情况。例如:
- 先固定价格,计算销售量变动对销售额的影响;
- 再固定销售量,计算价格变动对销售额的影响;
- 最后综合两个因素的作用,得到总变动。
这种方法可以逐步剥离各因素对结果的影响,分析过程清晰,便于掌握不同因素的独立作用。
因素分析法将总变动细分为若干因素变动的结果,帮助我们清晰认识不同因素的作用方向与强度。无论是两因素分析法、多因素分析法,还是综合因素分析法,都能有效揭示数据背后的驱动力,为管理决策、经营分析提供科学依据。
| 方法名称 | 适用情况 | 分析特点 | 示例说明 |
|---|---|---|---|
| 两因素分析法 | 总指标受两个因素影响 | 分别计算两个因素变动对总变动的影响程度和绝对效果 | 销售额增长由销售量、价格两因素变化引起 |
| 多因素分析法 | 总指标受三个及以上因素影响 | 综合分析多种因素对总变动的作用方向与贡献程度 | 销售额增长由销售量、价格、促销活动等多因素共同作用 |
| 综合因素分析法 | 多因素相互作用,需分步分析 | 逐一固定某些因素,测算其他因素变动对总变动的影响,最后综合汇总 | 先固定价格,计算销售量变动影响,再固定销售量,计算价格变动影响 |
2.3 两因素分析法:综合因素
两因素分析法是统计分析中最基本、最常用的因素分析方法,用于研究总指标受两个主要因素共同影响时,各因素变动对总变动的方向、程度与绝对效果。该方法通过计算因素指数、分解影响量,揭示不同因素对总量变动的贡献。
📈 综合因素分析方法步骤
- 确定总变动指标和两个影响因素
- 明确分析对象及相关的两个主要影响因素。
- 计算各因素指数
- 利用各因素的现期与基期数值,计算相应的变动指数。
- 根据公式计算因素影响量
- 采用标准公式,分解各因素对总变动的具体影响。
- 分析各因素变动的方向与程度
- 判断各因素是促进还是抑制总指标变动,量化贡献大小。
📈 案例分析
某省三种出口商品的统计资料如下表所示,要求据此分析出口商品价格、出口商品数量的变动对出口额的影响。
| 单位 | 出口数量 \(q_0\) | 出口数量 \(q_1\) | 出口价格(美元) \(p_0\) | 出口价格(美元) \(p_1\) | \(p_1 q_1\) | \(p_0 q_1\) | \(p_0 q_0\) |
|---|---|---|---|---|---|---|---|
| 大米 | 30 000 | 40 000 | 400 | 410 | 16 400 000 | 16 000 000 | 12 000 000 |
| 铜油 | 3 000 | 2 500 | 1 800 | 2 000 | 5 000 000 | 4 500 000 | 5 400 000 |
| 茶叶 | 1 300 | 1 700 | 2 300 | 2 400 | 4 080 000 | 3 910 000 | 2 990 000 |
| 合计 | — | — | — | — | 25 480 000 | 24 410 000 | 20 390 000 |
计算过程
-
出口额指数:
\[K_q = \frac{\sum p_1 q_1}{\sum p_0 q_0} = \frac{25 480 000}{20 390 000} = 124.96\% \]\[\sum p_1 q_1 - \sum p_0 q_0 = 25 480 000 - 20 390 000 = 5 090 000 \text{(美元)} \] -
出口价格指数:
\[K_p = \frac{\sum p_1 q_1}{\sum p_0 q_1} = \frac{25 480 000}{24 410 000} = 104.38\% \]\[\sum p_1 q_1 - \sum p_0 q_1 = 25 480 000 - 24 410 000 = 1 070 000 \text{(美元)} \] -
出口量指数:
\[K_v = \frac{\sum p_0 q_1}{\sum p_0 q_0} = \frac{24 410 000}{20 390 000} = 119.72\% \]\[\sum p_0 q_1 - \sum p_0 q_0 = 24 410 000 - 20 390 000 = 4 020 000 \text{(美元)} \]
由此可知:124.96% = 104.38% × 119.72%;5 090 000 = 1 070 000 + 4 020 000
从以上计算可以看出:三种商品的出口价格上升了 4.38%,使出口额增加了 1 070 000 美元;三种商品的出口数量上升了 19.72%,使出口额增加了 4 020 000 美元。二者共同影响,使三种商品的出口额上涨了 24.96%,绝对额增加了 5 090 000 美元。
指数方法是用来综合反映和分析复杂经济现象变动情况的重要方法,其优势包括:
- 通过同度量因素将复杂现象标准化、可比化;
- 区分数量与质量变动,有助于理解变动内在结构;
- 明确分析多因素对总变动的方向、程度与贡献,为决策提供依据。
2.4 两因素分析:平均因素
加权算术平均数 \(\bar{x} = \frac{\sum x f}{\sum f}\) 受两个因素的影响:一个是变量值 \(x_i\);一个是变量值所出现的次数的结构 \(\frac{f_i}{\sum f}\)。如果平均数发生动态变化 \(\frac{\bar{x}_1 - \bar{x}_0}{\bar{x}_0}\),显然是 \(x\) 和 \(\frac{f}{\sum f}\) 影响的结果。这里所要研究的问题是如何使用指数体系进行平均指标变动的因素分析。
回顾总量指标两因素分析的原理,在分析 \(p\) 和 \(q\) 对 \(pq\) 的影响时,是分别编制 \(p\) 的指数 \(\frac{\sum p_1 q_1}{\sum p_0 q_1}\) 和 \(q\) 的指数 \(\frac{\sum p_1 q_1}{\sum p_1 q_0}\)。同理,要分析 \(x\) 和 \(\frac{f}{\sum f}\) 对 \(\bar{x}\) 变动的影响,就需编制关于变量 \(x\) 的指数和关于次数结构 \(\frac{f}{\sum f}\) 的指数,从而形成指数体系,进行平均指标变动的绝对量和相对量分析。
📈 基本公式
编制平均指标体系,关键是确定同度量因素的时期。可以遵循这样的原则:
- 编制关于 \(x\) 的指数,把同度量因素 \(x\) 的时期固定在报告期;
- 编制关于 \(\frac{f}{\sum f}\) 的指数,则把同度量因素 \(x\) 的时期固定在基期。
按照这一原则,平均指标两因素分析的指数体系为:
各指数的含义为:
- 指数 \(\frac{\sum x_1 f_1}{\sum x_0 f_0}\) 称为可变组成指数,它反映平均指标的实际变动方向和程度,分子分母的差额 \(\frac{\sum x_1 f_1}{\sum f_1} - \frac{\sum x_0 f_0}{\sum f_0}\) 是平均指标增减的绝对量。
- 指数 \(\frac{\sum x_1 f_1}{\sum x_1 f_0}\) 称为固定组成指数,因其固定了次数结构的影响而得名,它反映变量 \(x\) 的变动方向和程度,分子分母的差额 \(\frac{\sum x_1 f_1}{\sum f_1} - \frac{\sum x_0 f_1}{\sum f_1}\) 说明 \(x\) 对平均指标影响的绝对量。
- 指数 \(\frac{\sum x_0 f_1}{\sum x_0 f_0}\) 称为结构影响指数,它反映次数结构 \(\frac{f}{\sum f}\) 变动对平均指标的影响,分子分母的差额 \(\frac{\sum x_0 f_1}{\sum f_1} - \frac{\sum x_0 f_0}{\sum f_0}\) 说明影响的绝对量。
三个指数在相对数上构成等式:
绝对量上存在如下等式:
📈 案例分析
某企业职工的工资如下表所示,分析职工工资水平和工人结构的变动对平均工资的影响。
| 月工资(元) \(x_0\) | \(x_1\) | 工人数(人) \(f_0\) | \(f_1\) | \(x_1 f_1\) | \(x_0 f_1\) | \(x_0 f_0\) |
|---|---|---|---|---|---|---|
| 技术工 | 380 | 420 | 245 | 250 | 105 000 | 95 000 |
| 辅助工 | 200 | 220 | 120 | 800 | 176 000 | 160 000 |
| 合计 | — | — | 365 | 1 050 | 281 000 | 255 000 |
** (1) 可变组成指数:**
** (2) 固定组成指数:**
** (3) 结构影响指数:**
** 结果分析:**
从以上结果可以看出:由于工资水平上升 10.19%,总平均工资增加了 24.76 元;由于工人结构的变动率为 -24.3%,总平均工资减少了 77.96 元。两者共同影响的结果,使总平均工资下降 16.58%,每个工人的月工资减少 53.2 元。
📖 三、常见的统计指数
统计指数(Statistical Index) 是用来综合反映某一类经济现象随时间、地域或对象变化而变动程度的相对数。它是经济统计分析中的一种重要工具,能够反映经济活动的总体趋势和水平。常见的统计指数有价格指数、数量指数、价值指数、股票指数等。
3.1 居民消费价格指数(Consumer Price Index, CPI)
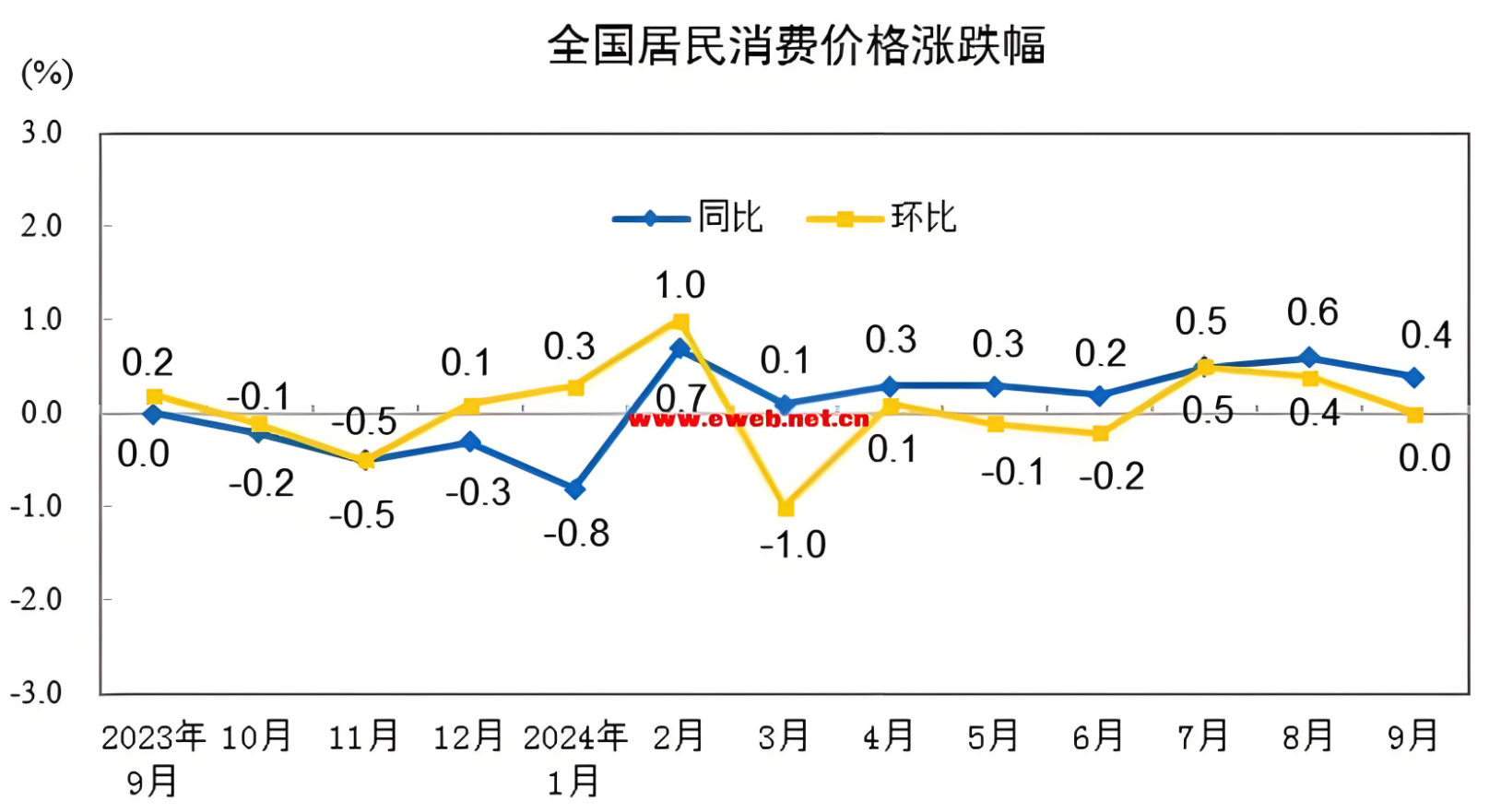
居民消费价格指数(CPI)是度量一定时期内城乡居民购买的消费品和服务项目价格水平变动情况的相对数,反映居民消费支出中价格变动对生活费用水平的影响。简言之,CPI 表示当前一篮子消费品和服务价格相对于基期价格的变动程度。
📌 计算方法
CPI 通常采用拉斯贝尔指数(Laspeyres Index)计算公式:
其中:
- \(P_{i1}\):报告期第 \(i\) 项商品或服务的价格
- \(P_{i0}\):基期第 \(i\) 项商品或服务的价格
- \(Q_{i0}\):基期第 \(i\) 项商品或服务的消费数量
- \(n\):商品或服务项目的种类数
说明:
以基期数量 \(Q_{i0}\) 作为权数,计算报告期价格变动对居民生活费用的影响。
- CPI = 100 表示价格水平不变
- CPI > 100 表示价格上涨
- CPI < 100 表示价格下降
📌 CPI 的分类与用途
-
分类
- 按消费内容分类:食品、衣着、居住、交通通信、教育文化娱乐、医疗保健等。
- 按用途分类:总体 CPI、核心 CPI(剔除食品和能源)、城市 CPI、农村 CPI。
-
用途
- 衡量通货膨胀或通货紧缩水平。
- 调整工资、养老金、社会福利。
- 政府制定货币政策、财政政策的重要依据。
📌 CPI 示例
例如,某地区基期居民主要消费三类商品:食品、衣着、居住,价格与数量如下表:
| 商品类别 | 基期价格(元) | 基期数量 | 报告期价格(元) |
|---|---|---|---|
| 食品 | 10 | 100 | 12 |
| 衣着 | 50 | 30 | 55 |
| 居住 | 500 | 5 | 550 |
代入公式计算:
计算分子:
- \(12 \times 100 = 1200\)
- \(55 \times 30 = 1650\)
- \(550 \times 5 = 2750\)
- 分子总和 = \(1200 + 1650 + 2750 = 5600\)
计算分母:
- \(10 \times 100 = 1000\)
- \(50 \times 30 = 1500\)
- \(500 \times 5 = 2500\)
- 分母总和 = \(1000 + 1500 + 2500 = 5000\)
最终 CPI:
表示居民生活费用水平上涨了 12%。
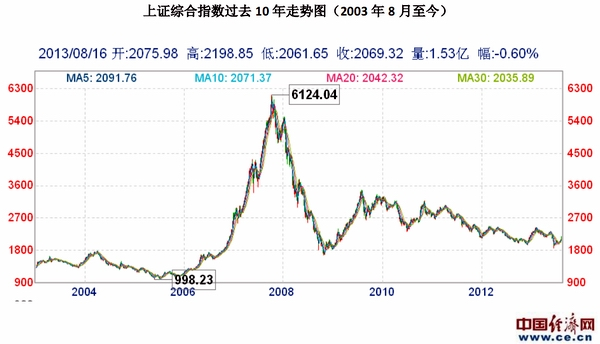
3.2 股票指数

股票指数(Stock Index)是反映股票市场整体价格水平变动和趋势的指标。它以某一时期或某种价格水平作为基准,衡量某一时期内一组代表性股票价格变动的平均水平。
📌 常见股票指数
| 指数名称 | 覆盖范围 | 地区 |
|---|---|---|
| 上证指数 | 上海证券交易所全部 A 股 | 中国 |
| 深证成指 | 深圳证券交易所主要上市公司 | 中国 |
| 恒生指数 | 香港证券交易所主要上市公司 | 香港 |
| 道琼斯工业指数 | 30 家大型工业上市公司 | 美国 |
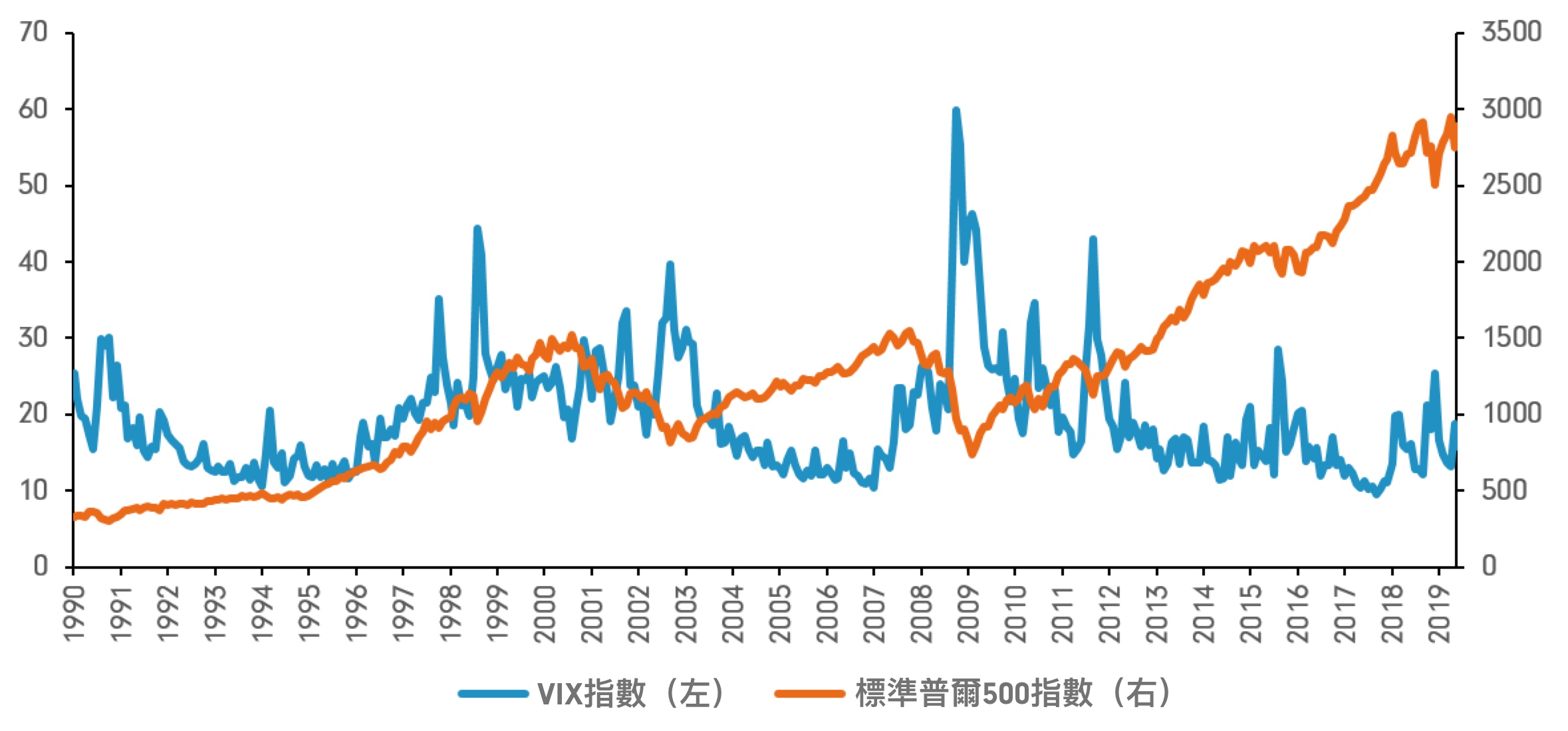
| 标普 500 指数 | 500 家大型上市公司 | 美国 |
| 纳斯达克综合指数 | 纳斯达克证券交易所全部上市公司 | 美国 |
📌 计算方法
(1)市值加权法
其中:
- \(P_{it}\):第 \(i\) 支股票在时间 \(t\) 的价格
- \(Q_{it}\):第 \(i\) 支股票在时间 \(t\) 的流通股数
- \(P_{i0}, Q_{i0}\):基期价格与数量
这是大多数现代指数(如上证指数、标普 500)采用的方法。
(2)价格加权法
例如,道琼斯工业平均指数就是将 30 只成分股的价格简单相加,除以调整除数得到指数值。
📌 股票指数作用
- 衡量股票市场整体价格水平变化。
- 判断股市总体运行趋势(牛市或熊市)。
- 作为基金、衍生品等金融产品的参考基准。
- 政府、投资者、研究机构的重要经济指标。
📖 总结
统计指数 是用来综合反映某一类经济现象随时间、地点或对象变动程度的相对数,是经济统计分析中的重要工具。它能够直观、简明地表达价格、数量、价值等经济指标的总体变动趋势。常见的统计指数包括居民消费价格指数(CPI)、股票指数、生产者价格指数(PPI)、进出口价格指数等。CPI 用于衡量居民购买消费品和服务价格的变动情况,反映生活费用水平的变化,常采用拉斯贝尔指数法计算。股票指数 则反映股票市场价格水平的整体变动趋势,常用市值加权法或价格加权法计算,如上证指数、道琼斯指数等。统计指数在经济监测、政策调控、投资决策和市场分析中发挥着重要作用,既能揭示经济总体走势,也能辅助微观分析,是现代统计分析与经济研究不可或缺的重要指标体系。
📖 参考文献



 浙公网安备 33010602011771号
浙公网安备 33010602011771号