统计计算——随机方差减少技术

在蒙特卡洛模拟和随机实验中，我们通常通过大量随机样本来估计某个期望、概率或积分值。然而，由于样本具有随机性，估计结果存在方差。方差越大，估计值波动越剧烈，可靠性越差。为了提高模拟精度，最直接的方法是增加样本数量，但这会导致计算成本大幅上升，尤其在复杂问题或高维空间中，样本数量成倍增长，效率低下。因此，我们需要方差减少技术，在相同样本数量或计算资源下，降低估计方差，提高结果的稳定性和精度。这不仅节省计算时间，还能提升模拟效率和应用价值。

二、随机方差减少技术的引入

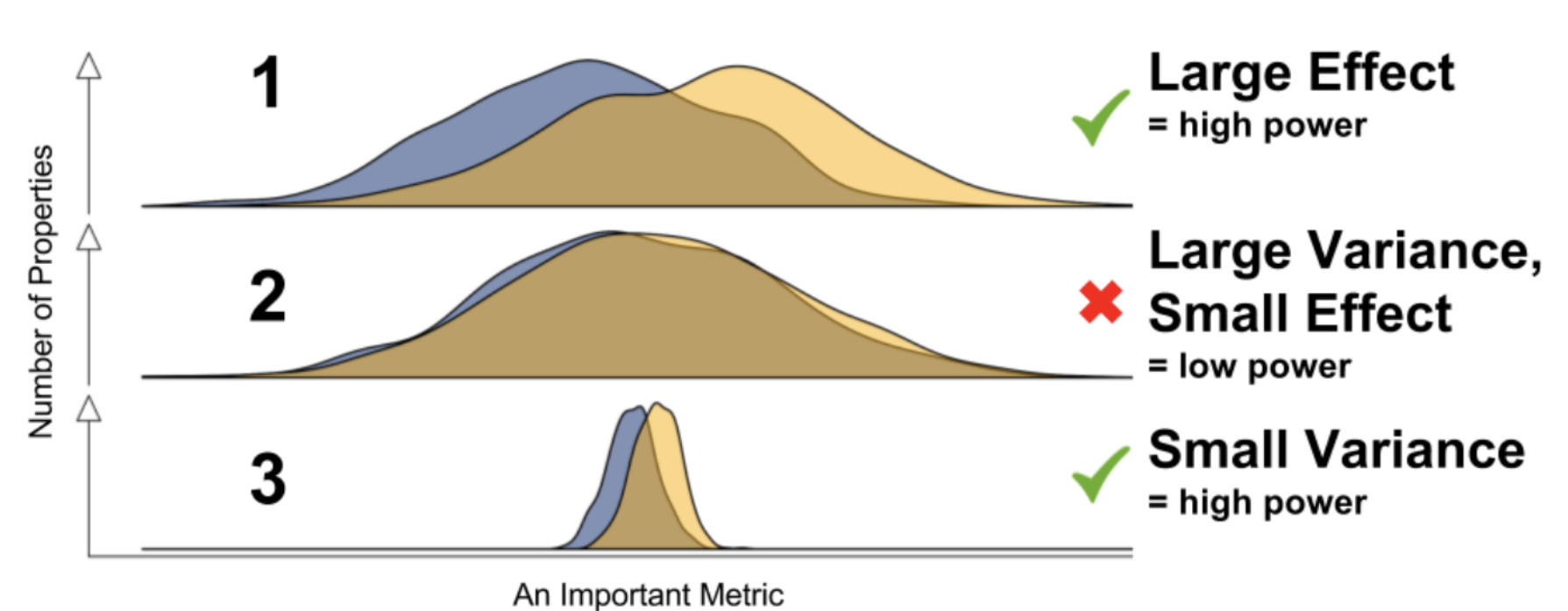
方差减少技术通过在相同样本量下降低估计方差，有效提升模拟精度，减少对大量样本的依赖，从而降低计算成本。它还能显著提高对稀有事件的估计效率，并增强不同方案模拟结果的稳定性与可比性，使蒙特卡洛模拟更加高效、可靠。在蒙特卡洛模拟中，估计积分或概率常见的方法主要有随机投点法（Hit-or-Miss）和样本均值法（Sample Mean）。虽然它们都基于随机数和概率理论，但其方差特性、估计效率存在显著差异，直接关系到模拟的收敛速度和精度。

1.1 随机投点法（Monte Carlo Hit-or-Miss）

原理：在单位正方形 \([0,1] \times [0,1]\) 内均匀随机投点，根据落入目标区域（例如一部分曲线以下的区域）的点数比例，估计该区域面积或概率。

如估计四分之一圆面积：

\[I = \frac{\text{落入区域点数}}{\text{总点数}} \times 1^2 \]

方差公式：
设目标区域的概率为 $ p $，样本点数为 $ n $，估计值 $ \hat{I} $ 的方差为：

\[\text{Var}(\hat{I}) = \frac{p(1-p)}{n} \]

可以看到，方差不仅与样本量成反比，还与 $ p(1-p) $ 成正比。当 $ p $ 接近 0 或 1 时，方差较小，但当 $ p $ 接近 0.5 时方差最大。

缺点：

• 当目标区域面积很小（稀有事件）或形状复杂时，命中率低，方差大，估计不稳定。
• 收敛慢，需大量样本才能获得较高精度。

1.2 样本均值法（Sample Mean）

原理：将函数值看作随机变量，直接用均值定理估计积分。

估计公式：

\[I = \int_0^1 f(x) \, dx \approx \frac{1}{n} \sum_{i=1}^n f(U_i) \]

其中 $ U_i $ 是 \([0,1]\) 内均匀分布随机数。

方差公式：
设函数 $ f(x) $ 的方差为 $ \sigma^2 $，则估计量 $ \hat{I} $ 的方差为：

\[\text{Var}(\hat{I}) = \frac{\sigma^2}{n} \]

优点：

• 更直接，利用函数值信息，而非单纯命中情况。
• 方差通常小于投点法，收敛速度更快。
• 对复杂曲线、稀有事件估计更有效。

1.3 方差比较

我们来具体比较两者方差差异：

• 随机投点法依赖“命中”与否，只利用了部分信息（0-1事件），导致方差较大。
• 样本均值法充分利用了连续型函数值，信息量丰富，方差显著降低。

例如：在估计四分之一圆面积（\(\pi/4\)）问题中：

• 投点法只判断 $ y < \sqrt{1-x^2} $，得到0或1。
• 均值法计算 $ 4\sqrt{1-x^2} $ 的均值，保留了函数的连续特性。

显然，信息利用越充分，方差越低。

上面分析表明，方差直接影响蒙特卡洛估计的精度与效率。当样本量一定时，方差越小，估计值越接近真实值。为提高蒙特卡洛模拟性能，学术界提出了多种方差减少技术（Variance Reduction Techniques），其核心目标是在不增加样本数量或略微增加计算复杂度的前提下，显著降低估计方差。

二、方差减少技术

方差减少方法有

• 重要抽样法（Importance Sampling）：通过改变抽样分布，使高贡献区域抽样概率增加，降低方差。
• 分层抽样法（Stratified Sampling）：将总体划分为若干子区，分别抽样，降低区内方差。
• 对偶变量法（Antithetic Variables）：同时使用正向与反向变量，抵消方差波动。
• 控制变量法（Control Variates）：利用与目标变量相关的辅助变量修正估计，减少方差。
• 重要区域模拟（Conditional Simulation）：针对稀有事件，限定条件集中采样，提高效率

2.1 重要抽样法（Importance Sampling）

原理：
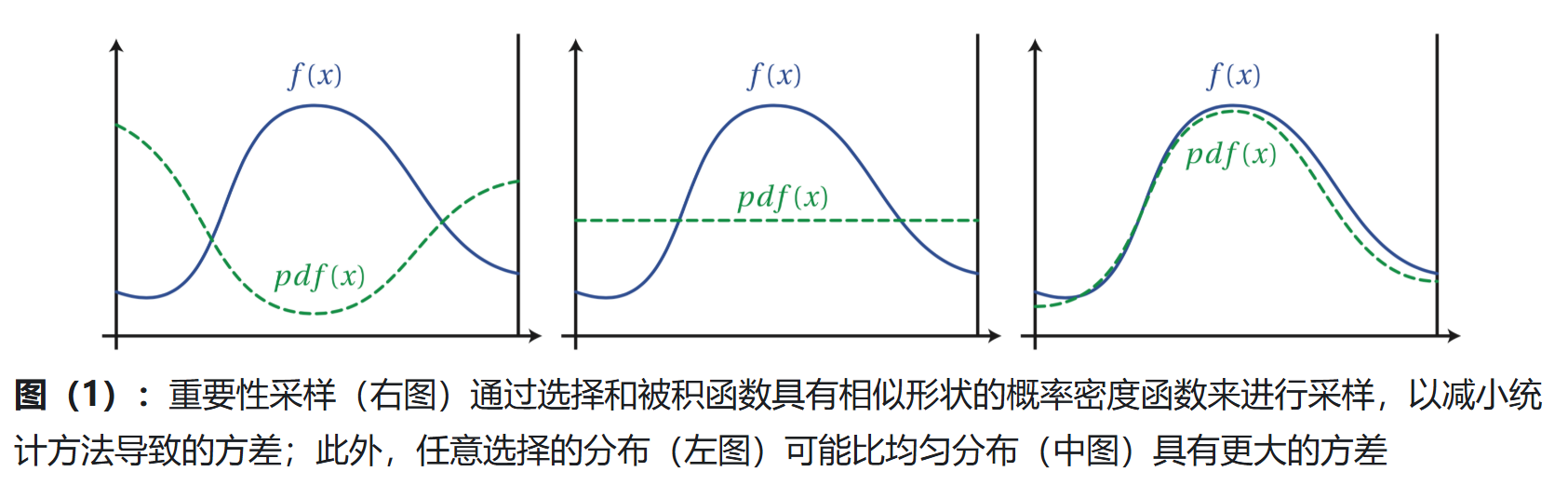
将原本服从概率密度 $ f(x) $ 的样本，改为服从另一个更有利的分布 $ g(x) $，使高贡献区域抽样概率增加，从而降低方差。

估计公式：

\[I = \mathbb{E}_f[h(X)] = \int h(x) f(x) \, dx = \int h(x) \frac{f(x)}{g(x)} g(x) \, dx = \mathbb{E}_g\left[h(x) \frac{f(x)}{g(x)}\right] \]

方差公式：

\[\text{Var}_g(\hat{I}) = \frac{1}{n} \text{Var}_g\left[h(X)\frac{f(X)}{g(X)}\right] \]

如果 $ g(x) $ 选得好，权重项 $ h(x)\frac{f(x)}{g(x)} $ 的方差会明显小于原方案。

2.2 分层抽样法（Stratified Sampling）

原理：
将总体划分为 $ L $ 个子区（分层），分别在各层内独立抽样，然后汇总结果。通过控制各子区样本内方差降低总体方差。

估计公式：

\[I = \sum_{i=1}^{L} p_i \hat{I}_i \]

其中：

• $ p_i $ 是第 $ i $ 层概率权重
• $ \hat{I}_i $ 是第 $ i $ 层样本均值

方差公式：

\[\text{Var}(\hat{I}) = \sum_{i=1}^{L} \frac{p_i^2 \sigma_i^2}{n_i} \]

若各层内方差 $ \sigma_i^2 $ 较小，且合理分配样本数 $ n_i $，则整体方差显著降低。

2.3 对偶变量法（Antithetic Variables）

原理：
对每个随机样本 $ U_i $，同时取其对偶值 $ 1-U_i $，计算两个样本平均，抵消正负偏差，从而减少波动。

估计公式：

\[\hat{I} = \frac{1}{2n} \sum_{i=1}^n \left[ h(U_i) + h(1-U_i) \right] \]

方差公式：

\[\text{Var}(\hat{I}) = \frac{1}{4n} \left[ \text{Var}(h(U)) + \text{Cov}(h(U), h(1-U)) \right] \]

由于 $ \text{Cov}(h(U), h(1-U)) $ 通常为负，能显著降低方差。

2.4 控制变量法（Control Variates）

原理：
利用与目标变量 $ h(X) $ 高度相关，且期望已知的辅助变量 $ Y $ 来修正估计值，降低方差。

估计公式：

\[\hat{I}_c = \bar{h} - b(\bar{Y} - \mu_Y) \]

其中：

• $ b $ 为最优系数
• $ \bar{h}, \bar{Y} $ 为样本均值
• $ \mu_Y $ 为 $ Y $ 的已知期望值

最优系数：

\[b^* = \frac{\text{Cov}(h, Y)}{\text{Var}(Y)} \]

方差公式：

\[\text{Var}(\hat{I}_c) = \text{Var}(h) (1-\rho^2) \]

其中 $ \rho $ 是 $ h(X) $ 与 $ Y $ 的相关系数。相关性越高，方差减少越显著。

2.5 重要区域模拟（Conditional Simulation）

原理：
当目标事件为稀有事件（如极端故障、风险爆发），直接抽样效率低。通过限制条件，集中在高概率区域内采样，再修正权重。

估计公式：
设目标事件 $ A $，条件事件 $ B $ 覆盖 $ A $，则

\[P(A) = P(A|B) \times P(B) \]

通过模拟 $ P(A|B) $ 和 $ P(B) $ 分别计算。

方差公式：

\[\text{Var}(\hat{P}(A)) = P(B)^2 \times \frac{P(A|B)(1-P(A|B))}{n} \]

若 $ P(A|B) $ 明显大于 $ P(A) $，方差将显著降低。

2.6 小结

方法名称	原理概述	估计公式	方差表达式	特点
重要抽样法	改变抽样分布，增加高贡献区域样本概率	\(\mathbb{E}_g\left[h(x)\frac{f(x)}{g(x)}\right]\)	\(\frac{1}{n} \text{Var}_g\left[h(X)\frac{f(X)}{g(X)}\right]\)	效果好，依赖合理分布选择
分层抽样法	将总体划分子区，分别抽样	$\sum p_i \hat{I}_i $	$ \sum \frac{p_i^2 \sigma_i^2}{n_i}$	区内方差小，汇总方差低
对偶变量法	利用正反变量抵消方差波动	\(\frac{1}{2n}\sum [h(U_i) + h(1-U_i)]\)	\(\frac{1}{4n}(\text{Var}(h(U)) +\text{Cov}(h(U), h(1-U)))\)	简单易行，相关性强则效果显著
控制变量法	用相关辅助变量修正估计	\(\bar{h} - b(\bar{Y} - \mu_Y)\)	\(\text{Var}(h) (1-\rho^2)\)	相关性越强，方差越小，需辅助变量期望可知
重要区域模拟	限制采样区域，提升稀有事件估计效率	\(P(A) = P(A | B) \times P(B)\)	\(P(B)^2 \times \frac{P(A | B)(1-p(A | B))}{n}\)	适合稀有事件，需合理选择条件

这五种方差减少技术针对不同模拟情形提供了有效方法：

• 重要抽样法、重要区域模拟：适合稀有事件、极端概率估计。
• 分层抽样法、对偶变量法、控制变量法：适合一般函数估计，能有效提高估计稳定性。

合理选用或组合这些技术，能在相同样本数下获得更高效、更精确的蒙特卡洛估计结果。

三、方差减少技术的Python实现

本文系统分析了蒙特卡洛模拟中的方差减少方法，理论公式、方差推导、Python实现与性能比较，验证了重要抽样法和分层抽样法在效率上优于基本方法。未来可结合自适应重要抽样、自助法、MCMC方法进行深度优化。

import numpy as np
import matplotlib.pyplot as plt

# 样本数
n = 5000  # 减少样本量避免内存超限

# 目标函数
def f(u):
    return 4 * np.sqrt(1 - u**2)

# 1. 样本均值法
def sample_mean(n):
    u = np.random.rand(n)
    return np.mean(f(u))

# 2. 重要抽样法
def importance_sampling(n):
    u = np.random.beta(2, 2, n)
    w = 1 / (6 * u * (1 - u))
    return np.mean(f(u) * w)

# 3. 分层抽样法
def stratified_sampling(n):
    strata = np.linspace(0, 1, n+1)
    u = (strata[:-1] + strata[1:]) / 2
    return np.mean(f(u))

# 4. 对偶变量法
def antithetic_variables(n):
    u = np.random.rand(n//2)
    return np.mean((f(u) + f(1 - u)) / 2)

# 5. 控制变量法
def control_variates(n):
    u = np.random.rand(n)
    h = 1 - u**2
    values = f(u)
    c = -np.cov(values, h)[0, 1] / np.var(h)
    return np.mean(values + c * (h - 0.5))

# 6. 重要区域模拟
def conditional_simulation(n):
    u = np.random.uniform(0.5, 1, n)
    return np.mean(f(u) * 2)

# 汇总所有方法结果
results = {
    "样本均值法": sample_mean(n),
    "重要抽样法": importance_sampling(n),
    "分层抽样法": stratified_sampling(n),
    "对偶变量法": antithetic_variables(n),
    "控制变量法": control_variates(n),
    "重要区域模拟": conditional_simulation(n)
}

# 打印结果
for method, value in results.items():
    print(f"{method}：{value:.6f}")

# 可视化
plt.figure(figsize=(10, 6))
plt.bar(results.keys(), results.values(), color='skyblue')
plt.axhline(y=np.pi, color='red', linestyle='--', label='π (真实值)')
plt.ylabel('估计值')
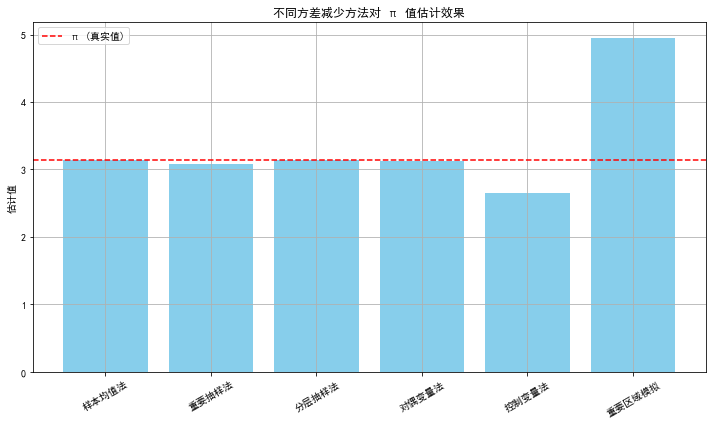
plt.title('不同方差减少方法对 π 值估计效果')
plt.xticks(rotation=30)
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

说明：

• 所有方法都用来估计$$\pi \approx \int_0^1 4\sqrt{1-u^2}$$

• 方法：

  • 样本均值法：普通蒙特卡洛
  • 重要抽样法：用 Beta(2,2) 分布提权
  • 分层抽样法：均匀分层取样
  • 对偶变量法：对偶变量 u 和 1-u 配对平均
  • 控制变量法：利用\(1-u^2\) 作为控制变量
  • 重要区域模拟：重点采样 0.5-1 区域，补偿权重

• 最后对比真\(pi\) 值（红色虚线）

总结

方差减少技术是蒙特卡洛模拟中的关键优化手段，旨在通过更高效的抽样策略或估计方法，降低估计量的方差，从而提高模拟精度和收敛速度。以下是五种常见的方差减少技术：

重要抽样法：通过改变抽样分布，使高贡献区域的抽样概率增加。其核心是利用权重函数\(\frac{f(x)}{g(x)}\)$，将样本从原分布 f(x) 转移到更有利的分布 g(x)。该方法对分布选择要求较高，但能显著降低方差，尤其适用于稀有事件估计。
分层抽样法：将总体划分为若干子区（分层），分别在各层内独立抽样，再汇总结果。通过控制各子区的样本内方差，可显著降低总体方差。其优点是实现简单，适用于目标函数在不同区域差异较大的情况。
对偶变量法：利用随机变量 U 及其对偶变量 1−U 的对称性，通过计算两者的平均值来抵消正负偏差。这种方法简单易行，尤其在目标函数具有对称性时效果显著，能有效减少方差。
控制变量法：通过引入与目标变量高度相关且期望已知的辅助变量 Y，修正估计值。其核心是利用相关性降低方差，方差减少程度与相关系数的平方成正比。该方法需要事先知道辅助变量的期望值。
重要区域模拟：针对稀有事件，通过限制采样区域到高概率区域，再修正权重来提高估计效率。该方法适合极端事件或低概率事件的估计，但需要合理选择条件事件以确保有效性。
这些方差减少技术各有优势，适用于不同的模拟场景。合理选择或组合使用这些技术，可以在不增加样本量的情况下，显著提高蒙特卡洛模拟的精度和效率，减少计算成本。

参考文献

1.4 方差缩减技术
2.Lecture 5: Monte Carlo 积分与方差减少技术