石头剪刀布——简单游戏中的博弈论智慧
“石头剪刀布”是一种简单而广为人知的手势游戏,其起源可以追溯到古代中国。据历史记载,石头剪刀布最早可能起源于汉代(公元前206年—公元220年),当时被称为“手势令”或“划拳”,是中国古代酒令文化的一部分。这种游戏最初可能被用于娱乐或决策,后来逐渐演变为一种广泛流行的民间游戏。
关于“石头剪刀布”的具体起源,存在多种说法。一种观点认为,它与中国古代的“五行”哲学有关,石头、剪刀、布分别代表金、木、水等元素,彼此之间存在相生相克的关系。另一种说法认为,石头剪刀布可能是从古代武术或手势占卜中演变而来,后来通过丝绸之路传播到亚洲其他地区,并进一步传入欧洲。在日本,石头剪刀布被称为“じゃんけん”(Janken),并在江户时代(1603年—1868年)广泛流行。欧洲版本的石头剪刀布则被称为“石头剪刀纸”(Rock-Paper-Scissors),其规则与亚洲版本基本一致。尽管石头剪刀布的起源细节尚存争议,但其跨越文化和国界的传播历程,充分体现了这一游戏的普适性和魅力。如今,石头剪刀布已成为全球范围内广为人知的竞技小游戏,不仅用于娱乐,还常被用作解决争议或做出随机决策的工具。
| 博弈规则 | 策略选择 |
|---|---|
 |
 |
一、游戏的博弈描述
“石头剪刀布”可以用简单而经典的博弈论模型来描述,尽管其规则简单,但它涵盖了博弈论中的七个要素,包括博弈规则、收益矩阵、混合纳什均衡等。
1.1 博弈的七个要素
-
参与者(Players)
石头剪刀布是一个双人博弈,参与者为两位玩家,记为玩家A和玩家B。 -
策略集(Strategies)
每位玩家的策略集相同,包含三个策略: -
石头(Rock, R)
-
剪刀(Scissors, S)
-
布(Paper, P)
因此,玩家A和玩家B的策略集均为\(S_A = S_B = \{R, S, P\}\)。
-
行动顺序(Order of Play)
石头剪刀布是一个同时行动博弈,双方同时出拳,不存在先后顺序。 -
信息集(Information Set)
双方在出拳前无法知道对方的选择,因此这是一个完全信息博弈。每位玩家在决策时只知道对方的策略集,而不知道对方的具体选择。 -
收益(Payoffs)
游戏的收益基于胜负关系: -
胜者得1分,败者得-1分。
-
如果平局,双方得0分。
收益函数可以表示为:
其中,$ s_A $ 和 $ s_B $ 分别表示玩家A和玩家B的策略。
-
结果(Outcomes)
游戏的结果取决于双方选择的策略组合,可能是胜、负或平局。 -
均衡(Equilibrium)
石头剪刀布的均衡是混合策略纳什均衡,即双方以等概率随机选择石头、剪刀或布。
1.2 游戏规则
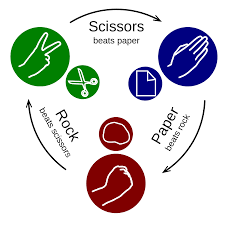
石头剪刀布的规则如下:
- 石头胜剪刀(R > S)
- 剪刀胜布(S > P)
- 布胜石头(P > R)
如果双方出拳相同,则为平局。
1.3 收益矩阵
收益矩阵展示了玩家A和玩家B在不同策略组合下的收益。
| A: 石头 (R) | A: 剪刀 (S) | A: 布 (P) | |
|---|---|---|---|
| B: 石头 (R) | (0, 0) | (1, -1) | (-1, 1) |
| B: 剪刀 (S) | (-1, 1) | (0, 0) | (1, -1) |
| B: 布 (P) | (1, -1) | (-1, 1) | (0, 0) |
收益分配规则:
- 如果A出石头,B出剪刀,A得1分,B得-1分。
- 如果A出布,B出石头,A得1分,B得-1分。
- 如果双方出拳相同,双方得0分。
二、纳什均衡
纳什均衡是博弈论中的一个核心概念,指的是在一个博弈中,所有参与者都选择了一个最佳策略,而且每个参与者在给定其他参与者策略的情况下,都没有动机单方面改变自己的策略。在纳什均衡中,每个参与者都处于“无悔”的状态,即如果对方的策略不变,那么自己选择的策略就是最优的。对于“石头剪刀布”游戏,可以观察到,如果两位玩家选择相同的策略,则游戏将平局(0,0)。如果玩家A选择石头,而玩家B选择剪刀,玩家A将获胜,反之亦然。由于这个游戏具有完全的信息和对称性,任何一方试图通过预测对方的选择来获得优势,都会被对方的选择所反制。因此,石头剪刀布并没有纯策略的纳什均衡,即不存在一个特定的策略总是能确保获胜,这时就要考察其混合纳什均衡。
2.1 设定混合策略
我们假设玩家A和玩家B采用混合策略,即他们以某种概率选择石头、剪刀或布。具体地,设:
- 玩家A选择石头的概率为 $ p_1 $,选择剪刀的概率为 $ p_2 $,选择布的概率为 $ 1 - p_1 - p_2 $。
- 玩家B选择石头的概率为 $ q_1 $,选择剪刀的概率为 $ q_2 $,选择布的概率为 $ 1 - q_1 - q_2 $。
2.2 计算期望收益
玩家A的期望收益 $ E_A $ 是在给定玩家B的混合策略下,玩家A选择不同策略时的加权收益。根据收益矩阵,我们可以得到:
- 如果A选择石头,A的期望收益为\[E_A(\text{R}) = 0 \cdot q_1 + 1 \cdot q_2 + (-1) \cdot (1 - q_1 - q_2) = 2q_2 - q_1 \]
- 如果A选择剪刀,A的期望收益为\[E_A(\text{S}) = (-1) \cdot q_1 + 0 \cdot q_2 + 1 \cdot (1 - q_1 - q_2) = 1 - 2q_1 - q_2 \]
- 如果A选择布,A的期望收益为\[E_A(\text{P}) = 1 \cdot q_1 + (-1) \cdot q_2 + 0 \cdot (1 - q_1 - q_2) = q_1 - q_2 \]
因此,玩家A的期望收益函数 $ E_A(p_1, p_2) $ 为:
类似地,玩家B的期望收益 $ E_B $ 是在给定玩家A的混合策略下,玩家B选择不同策略时的加权收益。根据收益矩阵,我们可以得到:
- 如果B选择石头,B的期望收益为\[E_B(\text{R}) = 0 \cdot p_1 + (-1) \cdot p_2 + 1 \cdot (1 - p_1 - p_2) = 1 - p_1 - p_2 \]
- 如果B选择剪刀,B的期望收益为\[E_B(\text{S}) = 1 \cdot p_1 + 0 \cdot p_2 + (-1) \cdot (1 - p_1 - p_2) = 2p_1 - p_2 \]
- 如果B选择布,B的期望收益为\[E_B(\text{P}) = (-1) \cdot p_1 + 1 \cdot p_2 + 0 \cdot (1 - p_1 - p_2) = p_2 - p_1 \]
因此,玩家B的期望收益函数 $ E_B(q_1, q_2) $ 为:
2.3 求解均衡
要找到混合纳什均衡,我们需要通过求解条件,使得每个玩家在给定对方策略的情况下,都没有单独改变自己的策略的动力。也就是说,我们要求在混合策略下,玩家A和玩家B的期望收益函数对于各自的策略概率分别最大化。
- 对玩家A而言,选择每个策略的期望收益需要对 $ p_1 $ 和 $ p_2 $ 求导,并设其为零,得到玩家A的最优策略。
- 对玩家B而言,选择每个策略的期望收益需要对 $ q_1 $ 和 $ q_2 $ 求导,并设其为零,得到玩家B的最优策略。
通过求导和解方程组,可以得出混合策略的均衡解为:
即玩家A和玩家B各自选择石头、剪刀和布的概率均为 $ \frac{1}{3} $。
2.4 计算均衡收益
由于两位玩家都以 $ \frac{1}{3} $ 的概率选择石头、剪刀和布,所以我们可以计算每个玩家在混合纳什均衡下的期望收益。
对于玩家A,使用期望收益公式,代入 $ p_1 = p_2 = \frac{1}{3} $ 和 $ q_1 = q_2 = \frac{1}{3} $,我们可以计算出玩家A的期望收益:
同理,对于玩家B,代入相同的值,我们可以计算出玩家B的期望收益:
在“石头剪刀布”的混合纳什均衡中,玩家A和玩家B的均衡收益都是0。这个结果反映了在该博弈中,尽管玩家在随机化选择中不会固定选择某一手势,但由于策略是完全均衡的,双方的期望收益最终相等,且都为0。换句话说,虽然每个玩家有可能在单局游戏中获胜,但从长期来看,双方的收益是平等的,处于博弈的均衡状态。
三、纳什均衡与游戏设计的公平性
纳什均衡不仅是博弈理论的重要组成部分,也是设计公平游戏的关键因素。通过理解纳什均衡及其应用,我们可以更好地设计游戏规则,确保游戏的公平性,使得每个参与者在博弈中都能获得合理的竞争机会。
-
纳什均衡的公平性
纳什均衡本质上是一种策略稳定性。假设在一个博弈中,参与者都能理性地选择策略且对对方的策略有所预期,纳什均衡则意味着每个参与者在该均衡状态下不会有动机单方面改变策略。在公平的博弈中,所有玩家在相同条件下都能公平地竞争,且每个玩家的期望收益应是均衡的。因此,纳什均衡为公平性提供了理论支持。
公平性不仅仅是指每个参与者在博弈中的机会均等,也涉及到收益的合理分配。在一个公平的博弈中,即使各方的策略和能力不同,均衡的存在能确保没有一方能通过操控规则或策略获得额外优势。对于参与者而言,博弈的公平性体现在他们采取的策略不会被其他玩家的策略“剥夺”优势,且每个玩家都能根据自己的信息作出最优选择。 -
博弈规则的公平性
在设计博弈时,公平性是一个重要的考虑因素。设计者希望通过设定合理的规则,确保每个参与者都有公平的机会来获得成功。在博弈设计中,纳什均衡的应用能够帮助实现这一目标。通过设定使得每个玩家都无法单方面改变结果的规则,设计者能够确保在多轮博弈中,所有参与者的策略选择都是经过深思熟虑且不容易被利用的。例如,在拍卖中,设计者通过设置合理的竞标规则,确保所有竞标者在规则下都能平等竞争,而不会因信息不对称或规则漏洞而造成不公平的结果。拍卖的均衡通常是在参与者都采取理性策略时形成的,这意味着每个人都以自己的最优策略进行竞标,并且在这种状态下没有人能通过改变自己的策略获得更大的利益。 -
公平性的挑战
尽管纳什均衡为博弈提供了理论上的公平性保障,但实际中,设计者仍面临一些挑战。一个重要的挑战是如何确保所有参与者都能获得平等的信息和资源。在现实世界中,信息不对称常常导致博弈的不公平。例如,在市场竞争中,一些公司可能通过垄断获取更多信息,而另一些公司由于资源和信息的限制,难以与其竞争。因此,在设计公平博弈时,设计者不仅要考虑规则的对称性,还要确保信息的透明性,避免任何一方通过不正当手段占得先机。
纳什均衡为博弈提供了一种稳定的状态,确保参与者在理性选择下无法通过单方面改变策略获得更大的收益,这为设计公平游戏提供了重要理论基础。在博弈设计中,通过合理的规则设定,确保每个参与者都能以公平的方式参与并竞争,避免信息不对称和不公正的规则,有助于实现博弈的公平性。然而,公平性的实现不仅仅依赖于规则的设计,还需要考虑参与者的信息获取、资源分配等多方面因素,以确保最终的结果是公平的,所有参与者都能在相对平等的条件下竞争。
四、“石头剪刀布”的哲学与社会借鉴
“石头剪刀布”是一种简单但深具哲学与社会意义的游戏,长期以来被广泛研究和应用。从博弈论的角度来看,它是一种典型的零和博弈,即一方的胜利意味着另一方的失败。在这个游戏中,石头克制剪刀,剪刀克制布,布又克制石头,形成一个封闭的循环,没有任何一种策略能够始终占据优势。这一特性在社会、经济、政治等诸多领域都有深刻的映射,反映了竞争、均衡、公平以及适应性的重要性。
-
博弈论视角下的公平性与均衡
“石头剪刀布”的最优策略是混合纳什均衡,即随机均匀地选择三种策略,确保不会被对手利用。这种均衡使得所有参与者的预期收益相同,避免了一方长期占优的情况。因此,该游戏被认为是公平竞争的典范,不存在最优的固定策略,每个玩家都在动态调整自己的选择,以适应对手的策略变化。这一理念被广泛应用于市场竞争、拍卖机制、甚至人工智能策略优化等领域,体现了公平性的重要性。 -
哲学上的循环与制衡
从哲学角度来看,“石头剪刀布”体现了一种动态的制衡法则,即任何优势都是相对的,且都会受到另一种力量的制约。在政治领域,不同政党或势力之间往往形成类似的相互牵制关系,没有任何一方能够长期垄断权力,必须通过不断的博弈与妥协来维持均衡。在商业竞争中,不同企业的市场策略往往呈现出类似的对抗关系,例如价格战、产品创新、品牌营销等策略之间相互克制,形成竞争格局的动态平衡。在科技发展中,一种新技术的出现可能会暂时领先,但往往会被新的创新所超越,这种技术更迭的循环促进了持续进步。这一循环制衡的原理告诉我们,没有绝对的赢家,唯一的生存之道是不断适应变化。在社会中,适者生存的道理同样适用,个人、企业乃至国家,都必须在不断变化的环境中调整策略,方能保持竞争力。 -
社会竞争中的策略与适应性
现实社会中,许多竞争关系类似于“石头剪刀布”的循环模式。例如,在商业领域,不同企业通过创新、营销和成本控制相互竞争,市场份额的变化往往呈现出动态均衡的特征。一个企业如果固守单一策略,很可能会被更灵活的竞争对手超越。因此,灵活应对、策略调整和适应环境变化是企业成功的关键。个人职场竞争也是如此。在工作中,单一的技能或优势并不能保证长期成功,员工需要不断学习新技能,以适应行业的发展变化。例如,技术人员需要跟进新技术,管理者需要提升领导能力,市场营销人员需要掌握最新的市场趋势。只有不断调整和优化自身的能力结构,才能在竞争中保持优势。 -
随机性与决策科学
“石头剪刀布”还体现了随机性在决策中的作用。在许多不确定的环境中,最佳策略往往不是固定的,而是基于概率分布的最优选择。在金融投资中,投资者通常不会把资金全部投入单一资产,而是进行资产组合,以降低风险。在战争战略中,军队的战术安排也往往带有一定的随机性,以避免被敌方预测和针对。这一点在人工智能的决策系统中也得到了应用。例如,在机器人对抗、自动驾驶等领域,AI 需要采用类似石头剪刀布的策略,以应对不断变化的外部环境。通过分析对手的行为模式,AI 可以调整自身的策略,使得长期收益最大化。 -
文化与社会心理的影响
“石头剪刀布”不仅是一种策略游戏,在不同文化背景下,它也承载着不同的社会心理和文化意义。在中国,这种游戏常用于决策,如在朋友间决定谁先行动、在儿童游戏中用作公平分配资源的方式。这体现了一种民主决策的思维,即在没有更优方案时,依赖随机性来达成公平的结果。此外,石头剪刀布的循环关系也影响了人们对公平与竞争的认知。在心理学研究中,有研究表明,人们在进行此类游戏时,会受到情绪、认知偏差和经验的影响,导致策略的变化。这种游戏心理学的研究可以用于解释金融市场的投资行为、竞标策略以及赌博心理。 -
机制设计的启示
从机制设计的角度来看,“石头剪刀布”的规则保证了所有玩家的公平性,但现实世界中的竞争往往没有这样完美的平衡。因此,许多社会机制都借鉴了类似的博弈模型来优化公平性,例如:
竞标系统:在拍卖机制中,设计者需要防止某一方占据过大的优势,确保竞标者的公平竞争环境。
市场监管:政府在监管市场竞争时,会引入类似的均衡机制,以防止某些企业长期垄断市场,保持行业的健康发展。
资源分配:在医疗、教育、住房等社会资源分配中,也常用博弈模型来优化公平性,以保证不同群体都能获得合理的资源。

总结
“石头剪刀布”不仅是一个简单的游戏,更是一种反映社会竞争、均衡与适应性的重要模型。它告诉我们,在竞争中,单一策略不可行,灵活应变才是关键;在社会中,没有永恒的赢家,动态均衡才是最稳定的状态。无论是在政治、经济、科技还是个人发展中,这一理念都提供了深刻的启示。石头剪刀布游戏作为经典的零和博弈,长期受到学者们的关注,尤其在博弈论、机制设计和人工智能领域。其独特的均衡性在于,每种策略既有克制对手的能力,也受另一种策略的制约,形成循环关系。这种特性导致纯策略纳什均衡不存在,但存在混合策略纳什均衡,即每个玩家以相等概率(1/3)随机选择石头、剪刀或布。这一均衡保证了游戏的公平性,使任何固定策略都无法占据长期优势。在博弈论研究中,石头剪刀布被用于分析最优随机化策略,即在竞争环境下,如何通过概率分布选择行动,以避免被对手预测。在机制设计中,该模型启示人们如何构建公平竞争机制,例如市场拍卖、资源分配等,以防止某一方长期占优。此外,在人工智能领域,该游戏成为训练强化学习算法的典型案例,帮助AI在对抗环境中学习如何制定最优策略。通过对石头剪刀布的研究,学者们揭示了博弈论中的随机性与均衡性原理,这不仅适用于游戏本身,还广泛应用于经济、社会及技术领域,推动了现代博弈理论的发展。
参考文献



 浙公网安备 33010602011771号
浙公网安备 33010602011771号