计量经济学(十四)——面板数据模型的固定和随机效应

面板数据模型是一类常见于经济学、社会科学等领域的计量经济模型，广泛用于分析具有时间维度和个体维度的多维数据。相比于传统的横截面数据模型或时间序列模型，面板数据模型能够更好地处理个体之间的异质性问题，并且提高模型的估计精度。通过对同一组个体（如公司、国家或个人）在不同时期的观测，面板数据模型可以同时捕捉个体内的时间变化和个体间的差异。在经济学研究中，面板数据模型常被用于研究企业行为、政策效果等动态过程。例如，通过对多个国家在多个年份的经济指标进行分析，面板数据模型可以帮助我们深入理解国家之间的差异以及政策实施前后的变化。由于面板数据既有时间序列维度，又有个体维度，因此在构建模型时需要特别考虑个体异质性的问题。为此，面板数据模型引入了固定效应模型和随机效应模型两种不同的方法，来处理个体特有的特征或随机影响。这里我们将详细介绍这两种模型的基本结构、参数估计方法和假设检验步骤。

---

一、面板数据

面板数据（Panel Data）是经济学、金融学和社会科学研究中一种非常重要的数据形式。它是在多个时间点上，对同一组个体进行观测所得到的数据。每一个个体（例如公司、国家、个人等）在每一个时间点上都有一组观测值，面板数据因此结合了横截面数据和时间序列数据的特点。横截面数据是指在某一特定时间点上对多个个体进行观测，而时间序列数据则是在不同时点上对单一对象进行观测。面板数据既能反映不同个体之间的差异，也能展示个体随时间的动态变化。

---

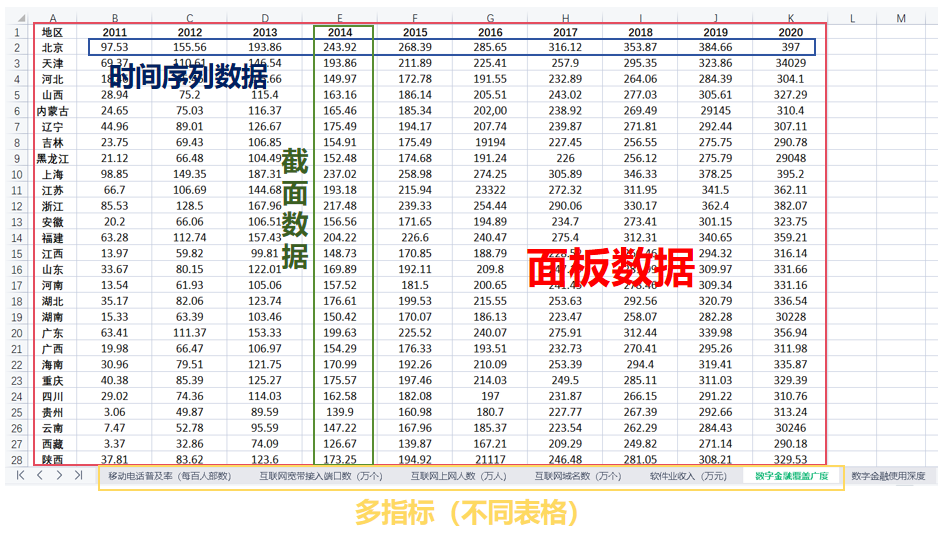
1.1 面板数据的描述与特点

面板数据与纯粹的横截面数据和时间序列数据相比，具有一些独特的优势。首先，它能够捕捉到个体之间的异质性。每个个体的行为和特征可能由于不可观测的因素（例如，公司的管理风格、文化或技术水平）而有所不同，面板数据可以有效地控制这些不可观测的个体差异。如果只使用横截面数据，我们无法控制这些差异；如果只使用时间序列数据，观测维度仅限于时间变化，无法考虑个体之间的差异。
其次，面板数据可以揭示时间维度上的动态变化。例如，随着时间的推移，个体的行为、政策的效果或者经济环境都会发生变化，而面板数据能够通过时间序列的维度反映这些变化。时间序列模型虽然可以揭示单一对象的动态，但无法同时考虑多个个体之间的异质性。相比之下，面板数据通过横截面维度控制了个体之间的差异，再通过时间维度捕捉动态变化，从而提高了模型估计的精度。
举例来说，如果我们追踪若干家公司的财务数据，比如收入、支出、利润等，在多个年份内的表现变化，这样的多维数据集就是典型的面板数据。通过面板数据分析，我们不仅能观察到公司之间的差异，还能考察各公司财务状况随着时间的变化趋势。
面板数据的另一个优势是它能够缓解遗漏变量偏差问题。假设有一些变量无法直接观测或数据无法获取，而这些变量对因变量有显著影响，面板数据模型可以通过控制个体效应来减少遗漏变量带来的偏差。例如，公司的企业文化或领导风格可能影响到其利润，但这些因素很难量化。在面板数据模型中，这些不可观测因素可以通过引入个体固定效应或随机效应来加以控制，从而减少遗漏变量的影响。

1.2 面板数据模型的应用场景

面板数据模型在多个研究领域中有广泛的应用，尤其是在经济学、金融学和社会科学领域。

• 企业行为的研究
  在研究企业行为时，面板数据模型经常被用来分析公司的生产效率、投资决策或经营绩效。通过对多个公司的多期数据进行分析，研究者可以识别出企业之间的差异，甚至可以研究不同时间段内企业行为的变化。例如，使用面板数据模型可以研究在全球金融危机期间，不同公司的资本结构如何调整，或者企业在危机前后在研发投资方面的策略变化。
• 宏观经济政策的效果评估
  面板数据模型也广泛应用于宏观经济学中，尤其是在评估政策效果时。通过对多个国家或地区的面板数据进行分析，研究者可以更精确地评估特定政策的效果。例如，研究者可以使用面板数据模型来分析不同国家在不同年份中对货币政策或财政政策的反应。这样，政策效果的动态特征可以得以体现，而个体（国家或地区）之间的特定差异（如政治制度、经济发展水平等）也可以通过模型中的个体效应加以控制。
• 个体或家庭消费行为的分析
  在社会科学和微观经济学中，面板数据模型常用于研究个体或家庭的消费习惯、劳动供给、收入波动等。通过对同一组家庭或个人在不同时期的消费、收入、储蓄等进行追踪，研究者可以分析个体消费行为的长期变化趋势，以及政策变化（如税收政策、福利政策）对家庭决策的影响。例如，研究可以分析家庭在税收政策改革前后的储蓄习惯变化。
• 金融市场分析
  在金融学领域，面板数据模型常用于研究股市、债市以及其他金融市场中的动态变化。例如，通过对多家公司的股价、财务指标、投资者行为等进行面板数据分析，研究者可以发现公司在不同宏观经济环境下的表现差异，并研究金融市场中的系统性风险和个别风险如何影响公司的股价波动。
• 健康与公共政策
  面板数据模型也被广泛应用于健康和公共政策领域。例如，研究者可以分析多国或多地区的医疗政策对人口健康的影响。通过对多年的医疗数据进行分析，能够揭示出不同医疗政策对健康结果的长期影响。

---

二、面板数据三大模型

面板数据（Panel Data）是指对同一组研究对象在不同时间上的重复观测数据，既包含横截面信息，又包含时间序列信息。其分析方法可充分利用数据的多维特征，控制不可观测的个体差异，提高估计效率与因果解释力。面板数据分析中，三种最常用模型是 固定效应模型（FE）、混合估计模型（POOL） 和 随机效应模型（RE）。它们的差异主要体现在对个体效应 \(\alpha_{i}\)​ 的处理方式和假设上。这里将以一个收入-教育-性别的经济学案例为背景，系统说明三类模型的理论框架、假设、估计方法与适用情境，并给出模型间的演变逻辑。

2.1 问题背景与总模型设定

设有 \(N\) 个个体（例如家庭、企业或地区）在 \(T\) 个时期的数据。假设研究目标是评估教育程度与性别对收入的影响，基本模型可写作：

\[I N C_{i t} = \alpha + \beta E D U_{i t} + \gamma G E N D E R_{i t} + \alpha_{i} + u_{i t} , i = 1 , \ldots , N ; t = 1 , \ldots , T \]

• \(I N C_{i t}\)：第 \(i\) 个个体在第 \(t\) 期的收入；
• \(E D U_{i t}\)​：受教育程度；
• \(G E N D E R_{i t}\)​：性别（0/1变量）；
• \(\alpha_{i}\)​：个体特有的不可观测效应，如先天才能、家庭背景；
• \(u_{i t}\)​：随时间变化的随机扰动。

关键问题是：如何处理\(\alpha_{i}\)？它既不随时间变化，又可能与解释变量相关或无关。不同假设会导致三种模型的产生。

2.2 POOL模型（混合估计模型）

模型假设

POOL模型（Pooled OLS 或合并横截面模型）假设不存在个体固定效应，或者认为不可观测效应对因变量无影响：

\[\alpha_{i} = 0 或 E \left(\right. \alpha_{i} \left.\right) = 0 \]

此时模型简化为：

\[I N C_{i t} = \alpha + \beta E D U_{i t} + \gamma G E N D E R_{i t} + u_{i t} \]

即直接将所有面板数据“堆叠”起来，忽略个体间差异，用普通OLS估计。

优缺点

• 优点：计算简单，适合快速探索平均效应。
• 缺点：若\(\alpha_{i}\)​真实存在且与\(E D U\)或\(GENDER\)相关，则遗漏变量偏误严重。

案例说明

在收入研究中，如果假设家庭背景或个人天赋不会显著影响教育与性别的关系，例如数据来自同质人群（如同一所学校的毕业生），可以直接使用POOL模型估计教育对收入的平均回报。

2.3 RE模型（随机效应模型）

模型假设

随机效应模型认为\(\alpha_{i}\)​存在，但它是随机变量且与解释变量不相关：

\[E \left(\right. \alpha_{i} \mid E D U_{i t} , G E N D E R_{i t} \left.\right) = 0 \]

模型可写作：

\[I N C_{i t} = \alpha + \beta E D U_{i t} + \gamma G E N D E R_{i t} + u_{i} + \epsilon_{i t} \]

其中 \(u_{i}\)​ 为个体随机效应，\(\epsilon_{i t}\) 为纯随机扰动。总体误差项为 \(u_{i} + \epsilon_{i t}\)，存在组内相关性，需采用广义最小二乘（GLS）或极大似然方法估计。

优缺点

• 优点：若假设成立，估计量比FE更有效率，可利用组间和组内两类信息。
• 缺点：若\(\alpha_{i}\)与解释变量相关，则估计有偏。

案例说明

假设教育程度主要由政策推动而非家庭背景决定，性别与教育分布无关，则个体天赋（\(\alpha_{i}\)​）虽然影响收入，但与教育、性别无关。此时可用RE模型，通过GLS获得更高效估计。该模型常用于全国抽样数据（如家庭追踪调查CFPS），个体差异视作随机扰动。

2.4 FE模型（固定效应模型）

模型假设

固定效应模型认为\(\alpha_{i}\)​存在且与解释变量相关，即：

\[E\left(\alpha_{i} \mid EDU_{it}, GENDER_{it}\right) \neq 0 \]

模型仍为：

\[INC_{it} = \alpha_{i} + \beta\,EDU_{it} + \gamma\,GENDER_{it} + u_{it} \]

为消除\(\alpha_{i}\)​影响，采用去均值变换（Within Transformation）：

\[I N C_{i t} - \left(\overset{ˉ}{I N C}\right)_{i} = \beta \left(\right. E D U_{i t} - \left(\overset{ˉ}{E D U}\right)_{i} \left.\right) + \gamma \left(\right. G E N D E R_{i t} - \left(\overset{ˉ}{G E N D E R}\right)_{i} \left.\right) + \left(\right. u_{i t} - \left(\overset{ˉ}{u}\right)_{i} \left.\right) \]

该方法通过个体内部时间变化估计\(\beta\)β与\(\gamma\)γ，有效控制所有不随时间变化的个体差异。

优缺点

• 优点：解决了不可观测异质性与解释变量相关导致的偏误问题，估计结果更具因果解释力。
• 缺点：无法估计随时间不变的变量（如性别），因为其组内变换为零；效率低于RE模型。

案例说明

若收入不仅受教育和性别影响，还受个人天赋影响，而天赋与教育高度相关（如聪明的人往往受教育更多），则必须用FE模型，通过控制个体固定效应排除偏误。例如同一个体在不同年份教育水平变化（进修学习）与收入变化的对应关系，可用FE估计教育的真实边际效应。

2.5 模型选择与应用

• 若\(\alpha_{i}\)​不存在或影响极小 → 采用POOL模型。
• 若\(\alpha_{i}\)​存在但与解释变量无关 → 采用RE模型。
• 若\(\alpha_{i}\)​存在且与解释变量相关 → 采用FE模型。

实践中常用 Hausman检验 判断FE与RE的适用性：

• 若检验显著，说明RE不满足独立性假设，应选FE模型；
• 若不显著，可用RE模型以获得更高效率。

面板数据分析核心在于处理不可观测的个体差异。POOL模型适合初步分析或同质样本，RE模型适合个体差异与解释变量无关的抽样数据，FE模型适合高度异质性且需要控制个体不变特征的研究。研究者需根据数据特征、研究目的及理论假设选择模型，并辅以Hausman检验验证模型选择。以教育对收入的影响为例，若忽略个体天赋，POOL估计可能夸大教育回报；若天赋与教育无关，RE模型可高效利用全部数据；若天赋与教育相关，则必须采用FE模型，控制个体效应后才能获得真实的教育回报率。这种模型演变体现了经济计量学在因果推断中从简单到严谨的逻辑过程。

---

三、固定效应模型

3.1 固定效应模型的表达

固定效应模型（Fixed Effects Model，FE）假设每个个体的不可观测特征是固定且不随时间变化的。换句话说，个体之间的差异被视为常数，可以通过引入个体特定效应来捕捉这些差异。

面板数据模型的一般形式为：

\[y_{it} = \alpha + \beta X_{it} + u_{it} \]

其中：

• $ y_{it} $ 是个体 $ i $ 在时间 $ t $ 的因变量；
• $ X_{it} $ 是个体 $ i $ 在时间 $ t $ 的自变量向量；
• $ \alpha $ 是常数项；
• $ u_{it} $ 是随机误差项。

在固定效应模型中，误差项可拆解为两部分：

\[u_{it} = \mu_i + \epsilon_{it} \]

其中：

• $ \mu_i $ 表示个体特定效应，在所有时间点保持不变；
• $ \epsilon_{it} $ 表示随机扰动项，满足经典线性回归假设。

因此，固定效应模型可写作：

\[y_{it} = \alpha + \beta X_{it} + \mu_i + \epsilon_{it} \]

3.2 参数估计方法

固定效应模型常用两种方法估计参数：

（1）差分法

适用于时间维度较短的面板数据，通过相邻两期作差消除个体效应：

\[y_{it} - y_{i,t-1} = \beta (X_{it} - X_{i,t-1}) + (\epsilon_{it} - \epsilon_{i,t-1}) \]

然后使用普通最小二乘法（OLS）进行估计。

（2）固定效应变换法（去均值法）

又称 Within Estimation，对每个个体取时间平均值：

\[\bar{y}_i = \alpha + \beta \bar{X}_i + \mu_i + \bar{\epsilon}_i \]

原方程减去均值后得到：

\[y_{it} - \bar{y}_i = \beta (X_{it} - \bar{X}_i) + (\epsilon_{it} - \bar{\epsilon}_i) \]

此时个体固定效应被消除，可用 OLS 估计 \(\beta\)。

3.3 固定效应模型的F检验

用于检验个体固定效应是否显著存在：

\[H_0: \mu_i = 0 \quad (\text{所有个体效应均为0}) \]

\[H_1: \mu_i \neq 0 \quad (\text{至少存在一个个体效应不为0}) \]

若拒绝 \(H_0\)，说明固定效应模型优于普通 OLS。

---

四、随机效应模型

4.1 随机效应模型的表达

随机效应模型（Random Effects Model，RE）假设个体特定效应是随机变量，记作 \(\mu_i\)，且与解释变量 \(X_{it}\) 不相关，满足：

\[\mu_i \sim N(0, \sigma_{\mu}^2) \]

模型形式为：

\[y_{it} = \alpha + \beta X_{it} + u_{it}, \qquad u_{it} = \mu_i + \epsilon_{it} \]

4.2 参数估计：广义最小二乘法（GLS）

由于误差项 \(u_{it}\) 包含个体随机效应，导致同一组内存在相关性，不能直接使用 OLS。解决方法是使用 GLS：

• 估计方差成分：估计 \(\sigma_{\mu}^2\) 和 \(\sigma_{\epsilon}^2\)。
• 构造协方差矩阵：反映误差项的相关结构。
• 加权变换：对原始数据加权，使误差项独立同分布。
• OLS 回归：在加权后的模型中使用 OLS 得到有效估计。

4.3 Hausman 检验

Hausman 检验用于选择 FE 或 RE 模型：

• 原假设 \(H_0\)：\(\text{Cov}(\mu_i, X_{it}) = 0\) （RE 一致且有效）
• 备择假设 \(H_1\)：\(\text{Cov}(\mu_i, X_{it}) \neq 0\) （需使用 FE）

检验统计量：

\[H = (b_{FE} - b_{RE})' [\text{Var}(b_{FE}) - \text{Var}(b_{RE})]^{-1} (b_{FE} - b_{RE}) \]

该统计量服从卡方分布，自由度等于解释变量数量。若 \(p\) 值显著，拒绝 \(H_0\)，选择固定效应模型。

4.4 固定效应与随机效应的比较

• 固定效应模型（FE）：
  将不可观测的个体特征视为固定参数，允许它们与解释变量相关。
• 随机效应模型（RE）：
  将不可观测的个体特征视为随机变量，假设其与解释变量独立。

研究企业规模对产值的影响：

• \(Y_{it}\)：第 \(i\) 个企业第 \(t\) 年的产值
• \(X_{it}\)：企业规模
• \(\gamma\)：企业类型、政策等不可观测特征

在 FE 中，\(\gamma_i\) 固定且与 \(X_{it}\) 相关；
在 RE 中，\(\gamma_i\) 随机且与 \(X_{it}\) 独立。

因此，选择模型的关键在于：不可观测特征与解释变量是否相关。

如果感觉抽象，可以根据一个实际例子进行理解：现在我们想探究企业规模和企业产值之间的关系，其中：\(Y_{i t}\) 为第 \(i\) 个企业第 \(t\) 年的产值，\(x_{i t}\) 为第 \(i\) 个企业第 \(t\) 年的规模， \(\varepsilon_{i t}\) 则为随机误差项。而 \(\gamma\) 表示企业的某些个体特征（比如说企业类型，管理者特质，享受政策等...），但是不同之处在于固定效应中认为这些个体特征为与个体有关，且不随时间改变，记为 \(\gamma_i\) ；但是随机效应中则认为，这些特征属于随机误差项，和个体以及时间都无关，记为 \(\gamma\) 。所以固定效应模型和随机效应模型的差别在于：遗漏的个体特征变量，究竟是算作解释变量，还是算作随机误差项？其中固定效应模型认为个体特征变量属于解释变量，随机效应模型则将个体特征变量考虑到随机误差项中。也正是如此，固定效应模型中的解释变量可以与个体特征变量相关，但是随机效应中不能。

---

五、案例分析

收集到1996-2002面板数据如下表，试通过地区人均收入解释地区人均消费的情况，并分析其固定效应和随机效应。蓝奏云数据下载链接https://wwxh.lanzouv.com/iEFwL2dc1dcj，解压后就是数据文件

地区	年份	地区人均消费	地区人均收入	地区	年份	地区人均消费	地区人均收入
安徽	1996	3282.466	4106.251	福建	1996	4011.775	4884.731
安徽	1997	3646.15	4540.247	福建	1997	4853.441	6040.944
安徽	1998	3777.41	4770.47	福建	1998	5197.041	6505.145
安徽	1999	3989.581	5178.528	福建	1999	5314.521	6922.109
安徽	2000	4203.555	5256.753	福建	2000	5522.762	7279.393
安徽	2001	4495.174	5640.597	福建	2001	6094.336	8422.573
安徽	2002	4784.364	6093.333	福建	2002	6665.005	9235.538
北京	1996	5133.978	6569.901	河北	1996	3197.339	4148.282
北京	1997	6203.048	7419.905	河北	1997	3868.319	4790.986
北京	1998	6807.451	8273.418	河北	1998	3896.778	5167.317
北京	1999	7453.757	9127.992	河北	1999	4104.281	5468.94
北京	2000	8206.271	9999.7	河北	2000	4361.555	5678.195
北京	2001	8654.433	11229.66	河北	2001	4457.463	5955.045
北京	2002	10473.12	12692.38	河北	2002	5120.485	6747.152

5.1 Python程序和结果输出

import pandas as pd
import statsmodels.api as sm
from linearmodels.panel import PanelOLS, RandomEffects, compare

# 从桌面加载 CSV 数据文件
file_path = 'data.csv'  # 请修改为正确的文件路径
df = pd.read_csv(file_path)  # 使用 read_csv 读取 .csv 文件

# 将地区和年份设置为索引，形成面板数据格式
df = df.set_index(['地区', '年份'])

# 定义因变量和自变量
Y = df['地区人均消费']
X = sm.add_constant(df['地区人均收入'])

# 固定效应模型
fixed_effect_model = PanelOLS(Y, X, entity_effects=True).fit()

# 随机效应模型
random_effect_model = RandomEffects(Y, X).fit()

# Hausman检验：用于比较固定效应和随机效应模型
result_comparison = compare({'Fixed Effects': fixed_effect_model, 'Random Effects': random_effect_model})

# 输出结果
print(fixed_effect_model.summary)  # 固定效应模型结果
print(random_effect_model.summary)  # 随机效应模型结果
print(result_comparison)  # Hausman检验结果

       PanelOLS Estimation Summary                           
================================================================================
Dep. Variable:                 地区人均消费   R-squared:                        0.9714
Estimator:                   PanelOLS   R-squared (Between):              0.9799
No. Observations:                 105   R-squared (Within):               0.9714
Date:                Fri, Oct 25 2024   R-squared (Overall):              0.9776
Time:                        19:14:53   Log-likelihood                   -673.02
Cov. Estimator:            Unadjusted                                           
                                        F-statistic:                      3020.6
Entities:                          15   P-value                           0.0000
Avg Obs:                       7.0000   Distribution:                    F(1,89)
Min Obs:                       7.0000                                           
Max Obs:                       7.0000   F-statistic (robust):             3020.6
                                        P-value                           0.0000
Time periods:                       7   Distribution:                    F(1,89)
Avg Obs:                       15.000                                           
Min Obs:                       15.000                                           
Max Obs:                       15.000                                           
                                                                                
                             Parameter Estimates                              
==============================================================================
            Parameter  Std. Err.     T-stat    P-value    Lower CI    Upper CI
------------------------------------------------------------------------------
const          515.61     81.597     6.3190     0.0000      353.48      677.74
地区人均收入         0.6976     0.0127     54.960     0.0000      0.6723      0.7228
==============================================================================

F-test for Poolability: 7.1518
P-value: 0.0000
Distribution: F(14,89)

Included effects: Entity
                        RandomEffects Estimation Summary                        
================================================================================
Dep. Variable:                 地区人均消费   R-squared:                        0.9757
Estimator:              RandomEffects   R-squared (Between):              0.9864
No. Observations:                 105   R-squared (Within):               0.9699
Date:                Fri, Oct 25 2024   R-squared (Overall):              0.9820
Time:                        19:14:53   Log-likelihood                   -687.28
Cov. Estimator:            Unadjusted                                           
                                        F-statistic:                      4142.9
Entities:                          15   P-value                           0.0000
Avg Obs:                       7.0000   Distribution:                   F(1,103)
Min Obs:                       7.0000                                           
Max Obs:                       7.0000   F-statistic (robust):             4142.9
                                        P-value                           0.0000
Time periods:                       7   Distribution:                   F(1,103)
Avg Obs:                       15.000                                           
Min Obs:                       15.000                                           
Max Obs:                       15.000                                           
                                                                                
                             Parameter Estimates                              
==============================================================================
            Parameter  Std. Err.     T-stat    P-value    Lower CI    Upper CI
------------------------------------------------------------------------------
const          345.18     80.365     4.2951     0.0000      185.79      504.56
地区人均收入         0.7246     0.0113     64.365     0.0000      0.7022      0.7469
==============================================================================
                    Model Comparison                    
========================================================
                         Fixed Effects    Random Effects
--------------------------------------------------------
Dep. Variable                   地区人均消费            地区人均消费
Estimator                     PanelOLS     RandomEffects
No. Observations                   105               105
Cov. Est.                   Unadjusted        Unadjusted
R-squared                       0.9714            0.9757
R-Squared (Within)              0.9714            0.9699
R-Squared (Between)             0.9799            0.9864
R-Squared (Overall)             0.9776            0.9820
F-statistic                     3020.6            4142.9
P-value (F-stat)                0.0000            0.0000
=====================     ============   ===============
const                           515.61            345.18
                              (6.3190)          (4.2951)
地区人均收入                          0.6976            0.7246
                              (54.960)          (64.365)
======================= ============== =================
Effects                         Entity                  
--------------------------------------------------------

5.2 结果解释

固定效应模型（FE）分析结果

R-squared（决定系数）

指标	数值	说明
R-squared (Within)	0.9714	解释面板内变化
R-squared (Between)	0.9799	解释地区间差异
R-squared (Overall)	0.9776	总体解释力

参数估计

参数	系数	T 值	P 值	解释
常数项 (const)	515.61	-	-	基线值（收入为0时消费水平，实际解释意义有限）
地区人均收入系数	0.6976	54.960	0.0000	每增加 1 单位收入，消费增加 0.6976 单位

F 检验与 Poolability 检验

检验类型	统计量值	P 值	结论
F-statistic	3020.6	0.0000	模型整体显著，收入对消费解释力强
Poolability 检验	7.1518	0.0000	地区差异显著，适合使用固定效应模型

---

随机效应模型（RE）分析结果

R-squared（决定系数）

指标	数值	说明
R-squared (Within)	0.9699	解释面板内变化
R-squared (Between)	0.9864	解释地区间差异
R-squared (Overall)	0.9820	总体解释力

参数估计

参数	系数	T 值	P 值	解释
常数项 (const)	345.18	-	-	基线值（收入为0时消费水平，实际解释意义有限）
地区人均收入系数	0.7246	64.365	0.0000	每增加 1 单位收入，消费增加 0.7246 单位

F 检验

检验类型	统计量值	P 值	结论
F-statistic	4142.9	0.0000	模型整体显著，收入对消费解释力强

---

固定效应与随机效应模型的比较（Hausman 检验）

比较指标	固定效应模型 (FE)	随机效应模型 (RE)	说明
R-squared	0.9714	0.9757	RE 略高于 FE
收入系数	0.6976	0.7246	两模型差异较小
检验结论	-	-	若拒绝 H₀ 选 FE，否则选 RE

• 如何选择模型：
  通常情况下，我们可以通过 Hausman检验 来判断是否应该使用固定效应模型还是随机效应模型。Hausman检验的主要目的是检测随机效应模型中的误差项是否与解释变量相关，如果存在相关性，随机效应模型会产生有偏估计。虽然在结果中没有直接展示 Hausman 检验的结果，但一般来说，如果 Hausman 检验的 P 值较小（例如小于 0.05），则倾向于使用固定效应模型。如果 P 值较大，则可以使用随机效应模型。总之，固定效应模型更适合解释地区内部变化的情况，能够有效控制不同地区的异质性。随机效应模型可以在考虑地区异质性的基础上估计出更好的整体效果，适用于数据符合随机效应假设的情境。在上面数据中，两个模型的效果都很好，但如果要进行模型选择，建议使用 Hausman 检验来进行最终判断。

总结

面板数据模型通过结合横截面数据和时间序列数据的优势，在处理数据中的异质性问题上具有显著优势。在分析复杂数据集时，面板数据模型能够有效控制个体间的异质性，减少由于忽略个体差异而导致的估计偏差。面板数据中的个体效应，即个体的不可观测特征，通常会对模型的解释变量产生影响，因此在模型构建中需要有效处理这些个体效应。
在固定效应模型中，个体效应被视为一个常数，不随时间变化。该模型通过去除个体间的固定差异来消除个体效应与解释变量之间的相关性，从而确保估计结果的一致性。这种模型适用于那些个体特征与解释变量密切相关的情境，因此能消除由个体间差异带来的潜在偏误。与之相对的，随机效应模型则假设个体效应是随机变量，且这些随机效应与解释变量不相关。这样做的目的是在提高估计效率的同时，充分利用数据的个体和时间信息。当个体效应与解释变量无关时，随机效应模型的估计更加高效。在实际应用中，研究者通常通过F检验来判断是否存在显著的固定效应，通过Hausman检验来比较固定效应模型与随机效应模型的适用性。通过这些工具，研究者能够选择最合适的模型，从而获得更加准确和一致的估计结果。

参考资料

1. 计量经济学导论16：面板数据模型
2. 人文李/面板数据模型
3. 面板数据：混合回归、随机效应、固定效应和双固定效应的介绍和选择

实例：交通事故死亡人数和酒精税

美国每年在高速公路上发生的交通死亡事故大约有 40,000 起。其中大约有三分之一的死亡事故是由酒后驾驶引发的，并且这一比例在酒精消费高峰期内呈上升趋势。如某研究（Levitt and Porter，2001）估计，在凌晨 1 点到 3 点的路上驾驶的司机中，有 25% 是酒后驾驶，而法律认定为喝醉的司机引发重大交通事故的可能性至少是没有喝酒的司机的 13 倍。
如何通过政府政策来抑制酒后驾驶，并通过这些政策降低实际的交通死亡事故。面板数据集中包含了与交通死亡事故和酒精消费有关的变量，其中包括每州每年的交通事故死亡人数、每州每年的酒后驾驶法律类型以及各州的啤酒税收。交通事故死亡人数用死亡率度量，即某州内总人口中每年每万人中死于交通事故的人数。酒精税用一种啤酒的“实际”税表示，即调整后的税，并用通货膨胀调整过的数值来衡量。

1982 年死亡率（FatalityRate）对啤酒税（BeerTax）的 OLS 回归线估计为：

\[\begin{aligned} \text{FatalityRate} = & 2.01 + 0.15 \text{ BeerTax (1982 年的数据)} \\ & (0.15)(0.13) \end{aligned} \]

其中啤酒税的系数为正，但在 10% 水平下统计不显著。由于我们有跨年的数据，所以我们可以用另一年的数据重新检验这种关系，1988年数据的 OLS 回归线为：

\[\begin{aligned} \text{FatalityRate} = & 1.86 + 0.44 \text{ BeerTax (1988 年的数据)} \\ & (0.11)(0.13) \end{aligned} \]

令人奇怪的是，1982 年和 1988 年数据中的系数估计值都为正，乍一看似乎较高的啤酒税导致更多的交通事故死亡人数，而不是更少。

由此我们就能得出结论：增加啤酒税会导致更多的交通事故死亡人数吗？不一定，这是因为这些回归中可能存在巨大的遗漏变量偏差。影响死亡率的因素有很多，包括州内的路面质量、高速公路的维修情况、驾驶的路程是乡下还是市内、路上的交通密度、社会文化是否接受酒后驾驶等，这些因素都有可能与酒精税收相关。如果这些因素与酒精税相关，则会导致遗漏变量偏差。一种解决这种遗漏变量偏差的方法是收集这些变量的数据，并将它们加到和回归模型中。
不幸的是，我们很难或不可能度量这些变量，比如酒后驾驶的文化接受度。但如果这些因素在给定某个州内不会随时间变化，那么我们可以采用另一种解决方法。因为我们有面板数据，即使我们无法度量这些不可观测因素，事实上我们可以通过固定这些因素不变来解决遗漏变量问题。为此采用固定效应 OLS 回归。

固定效应回归模型

当得到每个州 T=2 个时期的数据后，我们便可以比较第一个时期和第二个时期的因变量取值。这样，“前后”比较通过集中关注因变量的变化，实际上圈定了随个体（州）变化但不同时间变化的不可观测因素，达成经济学的“假设其他条件不变”。

现在，设决定第 \(i\) 个州死亡率的变量，但不同时间 \(t\) 变化（所以省略了下标 \(t\)）。例如 \(Z_i\) 表示酒后驾车的地方文化接受度，因为这种态度变化较缓慢，可以认为它在1982年和1988年之间保持不变。于是，联系死亡率和 \(Z_i\) 及啤酒税的总体线性回归为：

\[\text{FatalityRate}_{it} = \beta_0 + \beta_1 \text{BeerTax}_{it} + \beta_2 Z_i + u_{it} \]

其中 \(u_{it}\) 为误差项，\(i = 1, 2, \dots, n\)，\(t = 1, 2, \dots, T\)。

在上面回归模型中，\(Z_i\) 不随时间变化，因此不会引起1982年和1988年死亡率变化。故通过研究两个时期的死亡率变化分析可以消除这个回归模型中 \(Z_i\) 的影响。为了从数学上理解这一点，分别考虑1982年和1988年每一年的回归方程式，得：

\[\text{FatalityRate}_{1982} = \beta_0 + \beta_1 \text{BeerTax}_{1982} + \beta_2 Z_i + u_{i1982} \]

\[\text{FatalityRate}_{1988} = \beta_0 + \beta_1 \text{BeerTax}_{1988} + \beta_2 Z_i + u_{i1988} \]

两式相减就消除了 \(Z_i\) 的效应，得：

\[\text{FatalityRate}_{1988} - \text{FatalityRate}_{1982} = \beta_1 (\text{BeerTax}_{1988} - \text{BeerTax}_{1982}) + u_{i1988} - u_{i1982} \]

该设定形式有其直观解释。州内对酒后驾车的文化接受度影响了酒后驾车等的程度，进而影响了交通死亡率。但如果它们在1982年和1988年间保持不变，则它们不会引起州死亡率的变化。因此，随时间变化的死亡率净差是由其他原因引起的。换言之，分析 \(Y\) 和 \(X\) 的变化可以控制随时间不变的变量，于是就消除了这种产生遗漏变量偏差的来源，当数据是在不同年份里观测得到的时候，这种“前后”分析是有效的。