博弈论——颤抖手精炼纳什均衡(二十一)

在博弈论中，纳什均衡（Nash Equilibrium，NE）是博弈各方的一种策略组合，在这个组合下，每个参与者的策略都是对其他参与者策略的最优反应。换句话说，在纳什均衡下，任何一方都没有动机单方面改变自己的策略，因为那样做不会带来更高的收益。然而，纳什均衡的稳定性问题引发了大量的研究，特别是当我们考虑到现实中的人们有时会“犯错”或者随机地偏离最优策略时，传统的纳什均衡可能显得不够稳定。为了解决纳什均衡的稳定性问题，诺贝尔经济学奖得主 Reinhard Selten 提出了颤抖手精炼纳什均衡（Trembling Hand Perfect Nash Equilibrium，THPE），作为对纳什均衡的一种精炼（refinement）。这个均衡考虑了现实中决策者可能会犯错的情况，即参与者以极小的概率选择非最优策略。通过允许每个参与者的手“颤抖”一下，理论上能够更稳健地描述现实决策过程中的均衡，从而增强了纳什均衡的稳定性，是解决多重纳什均衡问题的一个途径。

一、颤抖手博弈的纳什均衡

在任何一个博弈中，每个局中人都有一个犯错误的可能性（类似一个人用手抓东西时，手一颤抖，他就抓不住他想抓的东西）。一个策略对是一个颤抖手精炼均衡时，它必须具有如下性质：各局中人\(i\)要采用的策略，不仅在其他局中人不犯错误时是最优的；而且在其他局中人偶尔犯错误（概率很小，但大于0）时还是最优的，可知颤抖手精炼均衡是一种较稳定的均衡。

1.1 颤抖手精炼纳什均衡的描述

颤抖手精炼纳什均衡是纳什均衡的一种更稳定的加强版本，它要求每个参与者的策略对手的颤抖（即他们选择非最优策略的极小概率）具有鲁棒性。具体来说，在颤抖手均衡中，参与者即使面对对手可能颤抖的情况，也必须选择能最大化其期望收益的策略。设想一个博弈中每个参与者都可能以极小的概率“犯错”，即以某个\(\epsilon> 0\) 的概率偏离最优策略。这时，参与者不能仅仅选择那些在某些情况下有更高回报的策略，而是必须选择在所有可能偏离情形下都能保证最优收益的策略。

定义与基本概念

设有限博弈 \(\Gamma=\{I,S,u\}\)，其中：

• \(I\) 表示玩家集合；
• \(S\) 表示策略集合；
• \(u\) 表示收益函数。

一个混合策略 \(\sigma_i\) 是完全混合策略（totally mixed strategy），如果它给每个纯策略都分配了正概率，即

\[\sigma_i(s_i) > 0, \quad \forall s_i \in S_i \]

一个策略组合 \(\sigma^*\) 被称为颤抖手精炼纳什均衡，如果存在一列完全混合的策略组合 \(\{\sigma^k\}\)，满足：

• \(\sigma^k \to \sigma^*\)（即该序列收敛于 \(\sigma^*\)）；
• \(\sigma^* \in \Delta\)（\(\Delta\) 是所有混合策略构成的策略空间）；
• 对每个玩家 \(i \in I\)，\(\sigma_i^* \in BR_i(\sigma^k_{-i})\)，即在对手采取“颤抖”（完全混合）策略时，\(\sigma_i^*\) 仍是最优反应。

换句话说，THPE 要求均衡解在对手可能有微小偏差的情况下依然保持稳健。这一额外的鲁棒性要求，能够剔除掉一些依赖弱劣策略（weakly dominated strategy）的均衡。

这里\(\sigma^*\) 为有限博弈的策略包：\(\sigma^*\) 是一个混合策略，表示博弈中各参与者在每个策略上选择的概率分布。
混合策略包 \(\{\sigma^k\}\)：表示博弈参与者所选择的混合策略的一个序列，其中每个策略组合都有一定的概率，且所有策略的概率大于0（即没有策略被完全忽略）。这个序列最终会收敛于一个特定的策略组合 \(\sigma^*\)。
混合策略空间 \(\Delta\)：\(\Delta\) 是所有参与者的混合策略构成的空间。
最优反应 \(BR_i(\sigma_{-i}^k)\)：\(BR\) 是 Best Response（最优反应） 的缩写。对每个博弈者 \(i\)，\(\sigma_i^*\) 是对其他博弈者策略组合 \(\sigma_{-i}^k\) 的最优选择，即在给定对手的策略情况下，博弈者 \(i\) 的策略选择能够使其收益最大化。

THPE 与 NE 的关系

定理1： 每个 THPE 必然是 NE。

设 \(\sigma\) 是 THPE。任取 \(\sigma'_i \in \Sigma_i\)，因为在收敛序列 \(\{\sigma^k\}\) 下，总有

\[U_i(\sigma_i,\sigma^k_{-i}) - U_i(\sigma'_i,\sigma^k_{-i}) \geq 0, \quad \forall n \]

利用收益函数的连续性，可得在极限下

\[U_i(\sigma_i,\sigma_{-i}) - U_i(\sigma'_i,\sigma_{-i}) \geq 0 \]

因此 \(\sigma_i\) 是 \(\sigma_{-i}\) 的最佳反应，从而 \(\sigma\) 是 NE。

这说明 THPE 在收敛极限下仍保持最佳反应性，因此必然是纳什均衡。

存在性定理

定理2： 任意有限标准型博弈至少存在一个THPE。

• 任取一个完全混合策略组合 \(\sigma^0\)。
• 对每个玩家 \(i\)，取一个序列 \(\epsilon_i^n \in (0,1)\)，且 \(\epsilon_i^n \to 0\)。
• 构造修正的效用函数：
  \[u^n_i(s) := U_i\Big(\big(\epsilon_i^n\sigma^0_i + (1-\epsilon_i^n)s_i\big)_{i \in I}\Big)，\quad \forall s \in S \]
  该函数表示：玩家以很小概率选择 \(\sigma^0_i\)（“颤抖”），以大概率选择原策略 \(s_i\)。
• 得到一个新博弈 \(G^n\)，由纳什均衡存在性定理，\(G^n\) 至少有一个纳什均衡 \(\sigma^n\)。
• 由于策略空间紧致，序列 \(\{\sigma^n\}\) 存在收敛子列，极限为 \(\sigma\)。
• 对每个满足 \(\sigma_i(s_i) > 0\) 的策略 \(s_i\)，存在整数 \(N(s_i)\)，使得当 \(n \geq N(s_i)\) 时，\(\sigma^n_i(s_i) > 0\)。取这些 \(N(s_i)\) 的最大值作为 \(N\)，则对所有 \(n \geq N\)，都有 \(s_i \in B_i(\sigma^n_{-i})\)。
• 极限点 \(\sigma\) 对所有在其支持集上的纯策略，都能在序列中保持正概率并且仍是最优反应，所以它满足 THPE 的定义。

颤抖手精炼纳什均衡通过引入“完全混合序列”的概念，把现实中可能的“颤抖”形式化，从而保证均衡在小概率错误存在的情况下依然稳定。它精炼了纳什均衡，排除了依赖弱劣策略的均衡点，更符合实际博弈中的理性与稳健性。因此，THPE 不仅在理论上具有重要意义，也为经济学、政治学、演化博弈等领域中的均衡选择提供了更合理的分析工具。

---

例1：囚徒困境博弈

博弈方1 \ 博弈方2	合作 (C)	背叛 (D)
合作 (C)	3, 3	0, 5
背叛 (D)	5, 0	1, 1

寻找颤抖手精炼纳什均衡的过程

• (D, D) 是一个纳什均衡，因为无论一方做什么，背叛都是另一个玩家的最佳选择。
• (C, C) 不是一个纳什均衡，因为背叛比合作有更高的收益。

颤抖手精炼
如果引入颤抖，即玩家可能会偶尔选择合作而不是背叛，那么我们要考虑微小概率的偏差对博弈的影响。

• (D, D) 是颤抖手精炼纳什均衡：即使有少量偏差，比如玩家偶尔选择合作，背叛仍然是每个玩家的最佳回应。这是因为无论另一方是否颤抖选择合作，选择背叛始终能带来更高的或不变的收益。因此，即使有偏差存在，背叛策略是稳定的。
• (C, C) 不是颤抖手精炼纳什均衡：因为如果一位玩家偶尔选择背叛，另一位玩家将失去所有的收益。因此，在偏差的情况下，玩家将偏向于选择背叛，从而使 (C, C) 不是一个稳定的颤抖手精炼纳什均衡。

结论
在这个囚徒困境博弈中，唯一的颤抖手精炼纳什均衡是 (D, D)。该例只有一个纳什均衡，由定理1可知颤抖手精炼纳什均衡。

1.2 颤抖手精炼纳什均衡的简化

假设一个博弈中有\(n\)个参与者，每个参与者\(i\)选择策略\(s_i\)的概率为 \(p_i(s_i)\)，并且存在一个很小的概率\(\epsilon_i\)表示参与者\(i\)选择“非最优策略”的概率。颤抖手精炼纳什均衡要求在每个参与者的策略中，任意小的\(\epsilon_i\) 偏差下，博弈的均衡解仍然保持稳定。也就是说，当\(\epsilon_i \to 0\)时，参与者的策略选择应该收敛于一个纯策略纳什均衡。

例2： 分析下面博弈的颤抖手精炼纳什均衡

博弈方1\博弈方2	L	R
U	10,0	6,2
D	10,1	2,0

在这个博弈中(D,L)和(U,R)都是纳什均衡，其中(D,L)对博弈方1较为有利，(U,R)对博弈方2较为有利，在不考虑选择和行为偏差的情况下，这两种纳什均衡都是稳定的。我们现在要判断的是它是否为颤抖手纳什均衡，即当博弈方有微小概率偏离其最优策略时，均衡是否仍然稳定。

(D, L) 是颤抖手精炼纳什均衡

博弈方2偏离策略分析
假设博弈方2有可能偏离 L，选择 R。我们设博弈方2选择 R 的概率为 $ a $，选择 L 的概率为 $ 1 - a $。
计算博弈方1的期望收益
博弈方1选择 U 时的期望收益：

• 当博弈方2选择 L（概率 $ 1 - a $），博弈方1的收益为 10。
• 当博弈方2选择 R（概率 $ a $），博弈方1的收益为 6。

期望收益 $ E(U) $ 为：$$ E(U) = (1 - a) \cdot 10 + a \cdot 6 = 10 - 4a $$

博弈方1选择 D 时的期望收益：

• 当博弈方2选择 L（概率 $ 1 - a $），博弈方1的收益为 10。
• 当博弈方2选择 R（概率 $ a $），博弈方1的收益为 2。

期望收益 $ E(D) $ 为：$$ E(D) = (1 - a) \cdot 10 + a \cdot 2 = 10 - 8a $$

比较期望收益

现在我们需要比较博弈方1在选择 U 和 D 时的期望收益：

\[E(U) = 10 - 4a \]

\[E(D) = 10 - 8a \]

为了找出博弈方1是否会选择 D 作为最优策略，我们比较两者：

\[E(D) \geq E(U) \]

即：

\[10 - 8a \geq 10 - 4a \]

化简：

\[-8a \geq -4a \]

\[a \leq 0 \]

因此，当 $ a = 0 $ 时，即博弈方2选择 L 的概率为 1（不偏离），博弈方1会选择 D。这个结论表明，(D, L) 是颤抖手精炼纳什均衡。

(U,R)不是颤抖手精炼纳什均衡

假设博弈方2“颤抖”
博弈方2选择R的概率为\(a\)，选择L的概率为\(1-a\)。接下来，我们计算博弈方1的期望收益。

计算博弈方1的期望收益
博弈方1选择U时的期望收益：

• 当博弈方2选择L（概率\(1-a\)），博弈方1的收益为10。
• 当博弈方2选择R（概率\(a\)），博弈方1的收益为6。

期望收益\(E(U)\)为：$$E(U)=(1-a)\cdot10+a\cdot6=10-4a$$

博弈方1选择D时的期望收益：

• 当博弈方2选择L（概率\(1-a\)），博弈方1的收益为10。
• 当博弈方2选择R（概率\(a\)），博弈方1的收益为2。

期望收益\(E(D)\)为：$$E(D)=(1-a)\cdot10+a\cdot2=10-8a$$

比较期望收益

我们需要比较博弈方1在选择U和D时的期望收益：

\[E(U)=10-4a \]

\[E(D)=10-8a \]

为了找出博弈方1是否会选择U作为最优策略，我们比较两者：$$E(U) \geq E(D)$$

即：

\[10-4a \geq 10-8a \]

化简：

\[-4a \geq -8a \]

\[a \geq 0 \]

这意味着只要博弈方2的偏离概率\(a\)不超过1，博弈方1选择U是其最优策略。

博弈方2的选择
现在考虑博弈方2的决策。如果博弈方2知道博弈方1选择U，那么博弈方2的收益为：

• 选择R时的收益是2。
• 选择L时的收益是0。

显然，博弈方2在这种情况下会选择R，因为2>0。

当我们引入颤抖手的概念时，博弈方1在考虑到博弈方2可能以小概率偏离R而选择L的情况下，会发现选择D比U更具稳定性。这意味着(U,R)在颤抖手均衡下并不稳定，因为博弈方1有动机选择D以应对博弈方2可能的偏差。因此，(U,R)不是颤抖手精炼纳什均衡。

二、颤抖手精炼纳什均衡

颤抖手精炼纳什均衡是对传统纳什均衡的扩展，它引入了博弈者偶尔可能犯错误的情况。颤抖手精炼纳什均衡不仅要求每个参与者的策略在面对对手的最优策略时是最优的，还要求即使对手偶尔出错，这种均衡策略也要具备稳定性。
在经典纳什均衡中，博弈者会假设其他博弈者完全理性，并且所有博弈者都会严格按照最优策略进行选择。然而，在实际决策过程中，博弈者可能会由于各种原因偶尔出错，即他们可能会选择并非最优的策略。为了应对这种可能性，颤抖手精炼纳什均衡提出了一种更稳健的策略选择方式，要求参与者在对手可能偶尔选择“错误”策略时，也能采取相对最优的策略回应。简言之，颤抖手精炼纳什均衡强调了稳健性。它不仅要求每个博弈者的策略在面对理性对手时是最优的，还要在对手偶尔“颤抖”选择非最优策略时，这个策略仍然能保证参与者的最大收益。

在演进博弈论中，颤抖手均衡尤其具有解释力。演进博弈论研究的是博弈双方通过一系列重复博弈形成的稳定策略，这种稳定性不一定来源于完全理性的策略计算，而可能是一种随机形成的过程。在这一过程中，博弈者会基于对对方行为的观察与猜测，逐步调整自己的策略，从而形成一种稳定的均衡。颤抖手均衡则解释了即使在对手偶尔出错的情况下，稳定的策略仍然能够维持。要将一种均衡定义为颤抖手精炼纳什均衡，必须满足以下两个关键条件：
策略的最优性：即使考虑到对手有可能颤抖（选择非最优策略），每个博弈者的策略仍然是最优的。换句话说，颤抖手纳什均衡不仅考虑了传统意义上的理性选择，还加入了应对不确定性和微小错误的策略。
策略的鲁棒性（稳健性）：在对手可能犯错的情境下，参与者的策略依然能为其带来最大利益。这一特征确保了颤抖手纳什均衡相比于传统纳什均衡更具稳定性和鲁棒性。

例3 考察下面博弈中的所有纳什均衡

一个博弈有可能存在很多个纳什均衡，对纳什均衡的精炼就是以不同的标准剔除在某一衡量标准下相对不合理或不稳定的纳什均衡而筛选出最合理或稳定的纳什均衡， 这个过程叫做纳什均衡的精炼(refinement)。颤抖手均衡是纳什均衡的一种精炼, 简单地说， 在一个纳什均衡状态，如果其中一个参与者的手颤抖了一下（假设为小概率事件）选择了次优的策略，那么一个纳什均衡是颤抖手均衡的要求就是参与者有动机重新回到原来的均衡，而不是这个偏离并趋向另一个纳什均衡。 如上图的例子， 图1显示这个博弈有两个纯策略纳什均衡，（A, A） 和 （B,B）, 收益分别是 （1，1） 和 （2，2） ；但颤抖手均衡只有一个，就是（A, A），收益为（1，1）。解释如下：
假设双方处于（A, A）这个纳什均衡， 如果参与者 I 颤抖，选择了B, 那么博弈的结果是 （B, A）,在 （B, A）, 参与者 I 有动机改变现状，因为选B的收益是0， 而选A的收益是1， 所以参与者 I 会重新选择A, 使博弈回到（A, A）这个均衡，对参与者 II 来说，（B,A）和（B,B）的收益是一样的，都是2，所以在（B,A）参与者II 没有动机改变现状。综上， 在（A,A）这个均衡，颤抖后博弈会重新回归这个均衡。直观地说（A,A）是抗震的，震完以后会归位。（A,A）就是一个颤抖手精炼纳什均衡。
相反，（B,B）就不是一个颤抖手精炼纳什均衡。
假设双方处于（B,B）, 收益 （2，2），如果有参与者颤抖，比如参与者II 颤抖到A，博弈结果成为（B, A）,收益变成 （0，2），在这个情况下，对于II 来说没有动机改变，因为颤抖前后收益都为2, 但对于I 来说，就不一样了，如果II 颤抖到A, I 的收益就从2变到0， 如以上所述，在（B,A）的情况下，I 有动机改变并选A。 所以，在(B,B)这个纳什均衡点，颤抖后均衡会趋向 （A,A）这个点，所以(B,B)就是在颤抖情况下不稳定的， （B,B）就不是一个颤抖手精炼纳什均衡。
在只有两个参与者的情况下，颤抖手精炼纳什均衡的一个充分必要条件是：是纳什均衡并且没有一个参与者的策略是弱劣策略（weakly dominated）。如图的列子里，B 对双方来说都是弱劣策略，所以根据这个充要条件，(B,B)可以被简单地剔除。

例4: 分析博弈的颤抖手精炼纳什均衡

考虑一个两人博弈，玩家1有策略三种：T、M、B，玩家2有三种策略：L、C、R。收益表如下：玩家1选择T时，无论玩家2如何选择，收益均为0；玩家1选择M时，玩家2选L收益为0，选C收益为1，选R收益为2；玩家1选择B时，玩家2选L收益为0，选C收益为0，选R收益为2。

Player1 \ Player2	$$L$$	$$C$$	$$R$$
$$T(p_1)$$	0, 0	0, 0	0, 0
$$M(p_2)$$	0, 0	1, 1	2, 0
$$B(1-p_1-P_2)$$	0, 0	0, 2	2, 2

1) 最佳反应（Best Responses）

先计算各纯列（玩家2 的 L、C、R）下玩家1 的收益，与各纯行（玩家1 的 T、M、B）下玩家2 的收益：

玩家1 对玩家2 各列的期望收益

• 对 L：\(u_1(T)=0,\; u_1(M)=0,\; u_1(B)=0\) ⇒ BR₁(L) = {T, M, B}。
• 对 C：\(u_1(T)=0,\; u_1(M)=1,\; u_1(B)=0\) ⇒ BR₁(C) = {M}。
• 对 R：\(u_1(T)=0,\; u_1(M)=2,\; u_1(B)=2\) ⇒ BR₁(R) = {M, B}。

玩家2 对玩家1 各行的期望收益

• 对 T：\(u_2(L)=0,\;u_2(C)=0,\;u_2(R)=0\) ⇒ BR₂(T) = {L, C, R}。
• 对 M：\(u_2(L)=0,\;u_2(C)=1,\;u_2(R)=0\) ⇒ BR₂(M) = {C}（注意：这里 R 的收益变为 0，因此 C 成为唯一最好反应）。
• 对 B：\(u_2(L)=0,\;u_2(C)=2,\;u_2(R)=2\) ⇒ BR₂(B) = {C, R}。

2) 纯与混合纳什均衡（NE）全集

纯策略 NE（双方互为最佳反应）有：

• \((T, L)\)：因 \(T\in BR_1(L)\) 且 \(L\in BR_2(T)\)。
• \((M, C)\)：因 \(M\in BR_1(C)\) 且 \(C\in BR_2(M)\)。
• \((B, R)\)：因 \(B\in BR_1(R)\) 且 \(R\in BR_2(B)\)。

关于混合 NE 的说明：
当玩家2 纯选 \(R\) 时，玩家1 的期望收益为

\[u_1(T)=0,\quad u_1(M)=2,\quad u_1(B)=2 \]

因此对 \(R\) 而言，玩家1 对 \(M\) 与 \(B\) 有一条由任意凸混合

\[\alpha M+(1-\alpha)B \quad (0\leq \alpha \leq 1) \]

（含端点）构成的最佳反应连续族。
这并不意味着这些配对都是纳什均衡：要成为均衡，玩家2 也必须对玩家1 的混合做出最优反应。
令玩家1 在 \(M,B\) 上的混合概率分别为 \(m\) 和 \(b\)（\(m+b=1\)），玩家2 的两个相关期望为

\[u_2(C)=m+2b, \qquad u_2(R)=2b \]

因此

\[u_2(C)-u_2(R)=m \]

由此可见，当 \(m>0\)（玩家1 对 \(M\) 赋予正概率）时，玩家2 对该混合会严格偏好 \(C\) 而非 \(R\)。
唯有在 \(m=0\)（即玩家1 纯为 \(B\)）的情形下，才有 \(u_2(C)=u_2(R)\)，此时 \(R\) 可以是玩家2 的最优反应。
因此尽管玩家1 对 \(R\) 的最佳反应形成一个连续族，但只有端点对应的纯策略 \((B,R)\) 能同时满足双方互为最佳反应的要求，从而成为真正的纳什均衡，其余混合点并非均衡。简言之：存在“对 \(R\) 的最佳反应的连续族”，但不存在以 \(R\) 为第二分量的连续族的混合纳什均衡；能构成均衡的只是纯点 \((B,R)\)。

因此 NE 全集为 \(\{(T,L),\ (M,C),\ (B,R)\}\)。

3) 弱劣（weak dominance）检查

比较各纯策略：

玩家1：

• 比较 M 与 T：在 L 上相等（0=0），在 C 上 M 更好（1>0），在 R 上 M 更好（2>0） ⇒ M 弱支配 T（T 被 M 弱支配）。
• 比较 M 与 B：在 L 上相等，C 上 M 更好（1>0），R 上相等（2=2） ⇒ M 弱支配 B（B 被 M 弱支配）。

玩家2：

• 比较 C 与 R：在 T 上相等（0=0），在 M 上 C 更好（1>0），在 B 上相等（2=2） ⇒ C 弱支配 R（R 被 C 弱支配）。
• L 在所有行上都为 0，而 C 或 R 在某些行上更高，故 L 被 C (和 R) 弱支配。

启示：任何包含被弱支配策略作出正概率选择的均衡，在颤抖手精炼下通常会被剔除。

4) 颤抖手精炼纳什均衡（THPE）严格检验

按照 Selten 的定义，用完全混合的颤抖序列检验极限点的稳健性。我们检验每一方在任一完全混合邻域（对手在其每一纯策略上都给正概率）下的唯一最优反应。

玩家1在完全混合下的唯一性

令玩家2 的完全混合为 \(q=(\ell,c,r)\)（\(\ell,c,r>0,\ \ell+c+r=1\)），玩家1 的三种期望：

\[u_1(T)=0,\qquad u_1(M)=c+2r,\qquad u_1(B)=2r \]

差值：

\[u_1(M)-u_1(B)=c>0,\qquad u_1(M)-u_1(T)=c+2r>0 \]

因此只要 \(c>0\)（即玩家2 在 C 上有正概率），M 在完全混合邻域中为玩家1 的唯一最优反应。

玩家2在完全混合下的唯一性

令玩家1 的完全混合为 \(p=(t,m,b)\)（\(t,m,b>0,\ t+m+b=1\)），玩家2 的三种期望：

\[u_2(L)=0,\qquad u_2(C)=m+2b,\qquad u_2(R)=2b \]

差值：

\[u_2(C)-u_2(R)=m>0,\qquad u_2(C)-u_2(L)=m+2b>0 \]

因此只要 \(m>0\)（玩家1 在 M 上有正概率），C 在完全混合邻域中为玩家2 的唯一最优反应。

由上，若存在一列完全混合策略 \(\{\sigma^k\}\) 收敛到某极限 \(\sigma^*\)，那么在每个完全混合 \(\sigma^k\) 中玩家1 的唯一最优反应为 M，而玩家2 的唯一最优反应为 C。换言之，极限点必须是 \((M,C)\)，且满足定义中“在序列中始终为最优反应”的要求。

因此，本博弈在当前矩阵下的唯一颤抖手精炼纳什均衡为：

\[\boxed{(M,\ C)} \]

5) 对三种 NE 的命运说明

• \((T,L)\)：虽然是 NE，但 T 与 L 都被弱支配（分别被 M 与 C/R 弱支配），因此在 THPE 下会被剔除。
• \((B,R)\)：尽管是 NE（纯 B, R），但 B 被 M 弱支配且 R 被 C 弱支配，因此在完全混合颤抖下它不稳健，也会被剔除。
• \((M,C)\)：既是 NE，又在任一完全混合邻域中分别为双方的唯一最优反应，因此是 THPE（且为唯一一个 THPE）。

6）可视化 best-response 与 **ε-颤抖数值图

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# 中文显示支持
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 玩家收益函数
u1_T = lambda q: 0
u1_M = lambda q: q[1] + 2*q[2]
u1_B = lambda q: 2*q[2]

u2_L = lambda p: 0
u2_C = lambda p: p[1] + 2*p[2]
u2_R = lambda p: 2*p[2]

# 构造概率网格
n = 100
q_grid = [(l, c, 1-l-c) for l in np.linspace(0,1,n) for c in np.linspace(0,1,n) if l+c<=1]
p_grid = [(t, m, 1-t-m) for t in np.linspace(0,1,n) for m in np.linspace(0,1,n) if t+m<=1]

# 最优反应计算
best1 = [np.argmax([u1_T(q), u1_M(q), u1_B(q)]) for q in q_grid]
best2 = [np.argmax([u2_L(p), u2_C(p), u2_R(p)]) for p in p_grid]

# ε-颤抖 收敛
epsilons = [10**(-k) for k in range(1,11)]
rows = []
for eps in epsilons:
    q = (eps/2, 1-eps, eps/2)
    p = (eps/2, 1-eps, eps/2)
    rows.append({
        "ε": eps,
        "u1(T)": u1_T(q), "u1(M)": u1_M(q), "u1(B)": u1_B(q),
        "u2(L)": u2_L(p), "u2(C)": u2_C(p), "u2(R)": u2_R(p)
    })
df = pd.DataFrame(rows)

# 绘图
fig, axes = plt.subplots(2,2,figsize=(12,9))

# 玩家1 best response
axes[0,0].scatter([l for l,c,r in q_grid],[c for l,c,r in q_grid],c=best1,cmap="Set1",s=10)
axes[0,0].scatter(0,1,c="red",marker="x",s=80,label="(M,C)")
axes[0,0].set_title("玩家1最佳反应区域")
axes[0,0].set_xlabel("L概率"); axes[0,0].set_ylabel("C概率")
axes[0,0].legend()

# 玩家2 best response
axes[0,1].scatter([t for t,m,b in p_grid],[m for t,m,b in p_grid],c=best2,cmap="Set1",s=10)
axes[0,1].scatter(0,1,c="red",marker="x",s=80,label="(M,C)")
axes[0,1].set_title("玩家2最佳反应区域")
axes[0,1].set_xlabel("T概率"); axes[0,1].set_ylabel("M概率")
axes[0,1].legend()

# 玩家1收益随ε
axes[1,0].plot(df["ε"], df["u1(T)"], label="u1(T)")
axes[1,0].plot(df["ε"], df["u1(M)"], label="u1(M)")
axes[1,0].plot(df["ε"], df["u1(B)"], label="u1(B)")
axes[1,0].set_xscale("log"); axes[1,0].set_title("玩家1收益随ε变化"); axes[1,0].legend()

# 玩家2收益随ε
axes[1,1].plot(df["ε"], df["u2(L)"], label="u2(L)")
axes[1,1].plot(df["ε"], df["u2(C)"], label="u2(C)")
axes[1,1].plot(df["ε"], df["u2(R)"], label="u2(R)")
axes[1,1].set_xscale("log"); axes[1,1].set_title("玩家2收益随ε变化"); axes[1,1].legend()

plt.tight_layout()
plt.show()

print("ε-颤抖下的收益表：")
print(df.to_string(index=False))

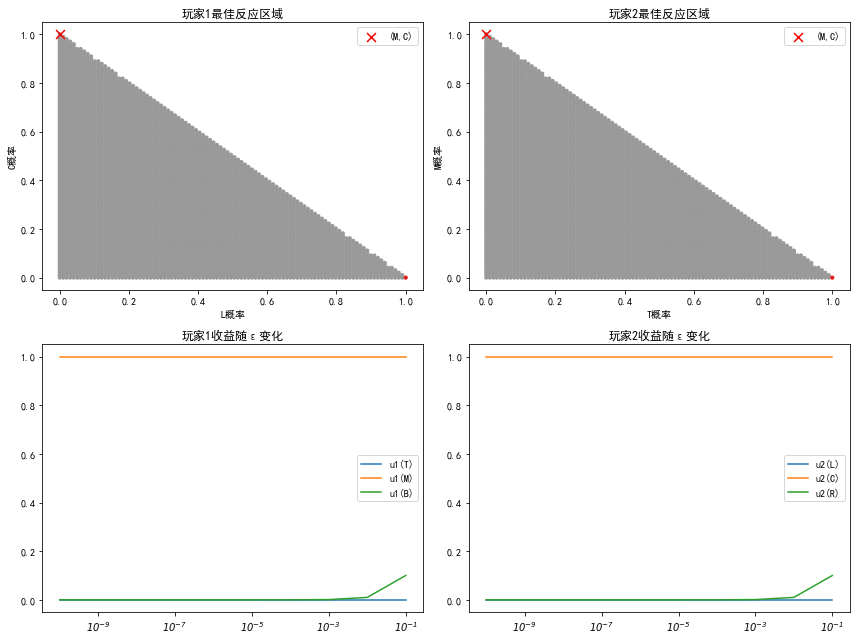
总结

颤抖手精炼纳什均衡（Trembling Hand Perfect Nash Equilibrium）是博弈论中对传统纳什均衡的扩展和加强。传统纳什均衡假设所有参与者都理性地选择最优策略，但在实际中，参与者可能会由于错误或其他不确定因素，偶然地选择非最优策略。颤抖手均衡通过引入参与者可能出现的“颤抖”——即轻微的非理性行为或策略偏离，从而使均衡在面对这种偶然“错误”时仍然保持稳定。换句话说，这一均衡要求策略不仅在当前情境下最优，而且在对手可能犯错的情况下也依然是最优的。
相比普通的纳什均衡，颤抖手精炼纳什均衡更加现实，因为它考虑了策略选择中的微小偏差，并确保均衡解在各种细微扰动下仍然成立。特别是在存在多重均衡的博弈中，颤抖手精炼均衡可以帮助筛选出更稳健的解，从而避免因策略偏差导致的不稳定现象。它不仅广泛应用于经济学中的市场进入博弈、拍卖博弈等，还在进化博弈论中用于解释物种如何形成稳定的行为策略。因此，颤抖手精炼纳什均衡为博弈论提供了一个更强的稳定性标准，它在面对具有多重均衡和不完全信息的博弈时，提供了更为精确的分析工具。

参考文献

1.博弈论新讲(5) 颤抖手精炼均衡
2.张维迎《博弈与社会》威胁与承诺（2）序贯理性