马尔科夫决策过程MDP——Agent的强化学习逻辑
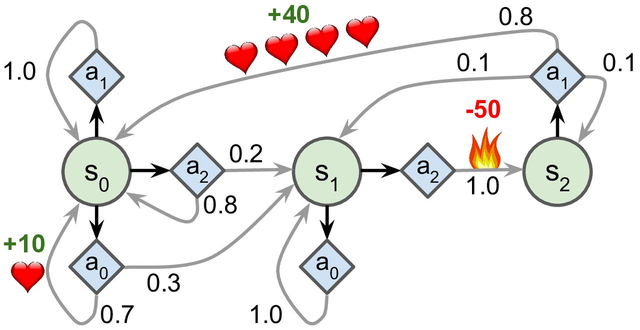
马尔可夫决策过程最初是在 20 世纪 50 年代由 Richard Bellman 描述的。它们类似于马尔可夫链,但有一个连结:在状态转移的每一步中,一个智能体可以选择几种可能的动作中的一个,并且转移概率取决于所选择的动作。此外,一些状态转移返回一些奖励(正或负),智能体的目标是找到一个策略,随着时间的推移将最大限度地提高奖励。马尔科夫决策过程(Markov Decision Process, MDP)是一个用于建模和解决序列决策问题的数学框架,尤其适用于在不确定环境下的决策。由于其简单性、动态特性和强大的理论基础,MDP在人工智能(AI)领域的应用变得尤为重要。
 |
 |
一、马尔科夫决策过程概述
在马尔可夫过程中,若状态变量 \(S_t\),则马尔可夫过程可用状态之间的内在关系来描述:
而在马尔科夫决策过程(Markov Decision Process, MDP)中,我们为系统增加一个行为(action)变量 $ A_t $ 与一个“奖励”(reward)变量\(R_t\)。其中\(A_t\)代表了我们“主观能动性”的部分,相当于系统的“输入”;而$ R_t $代表着在 $ t$ 时刻我们采取的行动带来的回报,相当于系统的“输出”。这样一来,在MDP中状态的转移关系不再是内在的,而是由状态 \(S_t\) 与输入的行动 $ A_t$ 共同决定。这也就是说,下一个时刻的状态 \(S_t\) 由转移概率模型决定:
而系统输出的奖励\(R_t\) 同样由概率分布决定,为了方便起见,也可以用随机变量 $ R_t(s_t, a_t)$ 表示:
MDP是一种用于建模决策问题的数学框架,尤其适用于那些在不确定环境下的序列决策问题。MDP由一组状态、一组动作、转移概率和奖励函数组成,通过这些元素,可以描述一个决策者在各个状态下的行为以及这些行为所带来的后果。MDP由以下五个要素构成:
状态集(State Space, S):表示系统可能处于的所有状态的集合。
动作集(Action Space, A):表示在每个状态下,决策者可以采取的所有可能动作的集合。
转移概率(Transition Probability, P):表示从一个状态转移到另一个状态的概率分布\(Pr(s'|s, a)\)。
奖励函数(Reward Function, R):表示决策者在某一状态采取某一动作后获得的即时奖励 \(R(s)\) 或 \(R(s,a)\)。
折扣因子:\(\gamma\)表示折扣因子。
MDP 的目标是找到一个策略(Policy, π),即在每个状态下选择一个动作的规则,使得在长时间内获得的累计奖励最大化。
例1:状态转移矩阵
| 状态转移图1 | 状态转移图2 |
|---|---|
 |
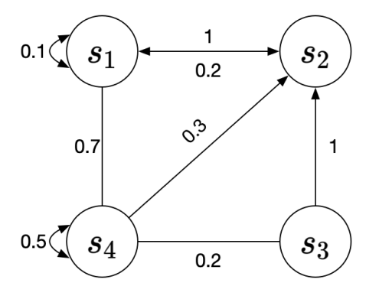 |
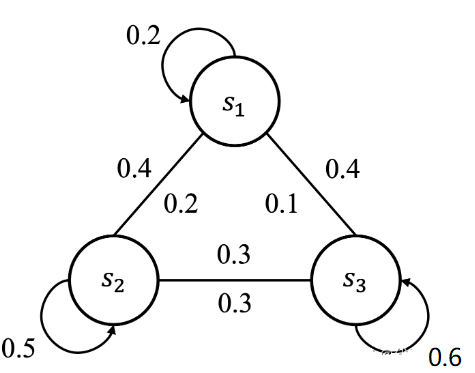
马尔可夫决策过程的状态流向,可用状态转移矩阵来刻画表示。但严格来说,状态转移图1并没有完整地描述马尔可夫决策过程,因为没有包含动作、奖励等因素,所以我们称之为马尔可夫链,同样也需要满足马尔可夫性质。我们用一个概率来表示状态间的切换,比如 \(P_{12}=P\left(S_{t+1}=s_2 \mid S_{t+1}=s_1\right)=0.4\) ,表示从当前认真听讲的状态 \(s_1\) 切换到玩手机的状态 \(s_2\) 的概率,我们把这个概率称为状态转移概率(State Transition Probability)。由于状态数是有限的,我们可以用下表来描述:
| $$S_{t+1}=s_1$$ | $$S_{t+1}=s_2$$ | $$S_{t+1}=s_3$$ | |
|---|---|---|---|
| \(S_t=s_1\) | 0.2 | 0.4 | 0.4 |
| \(S_t=s_2\) | 0.2 | 0.5 | 0.3 |
| \(S_t=s_3\) | 0.1 | 0.3 | 0.6 |
也可以用数学的矩阵来表示:
这个矩阵就叫做状态转移矩阵(State Transition Matrix),拓展到所有状态可以表示为:
例2:我在学习钢琴场景中,在这个过程中我就是智能体,而钢琴就是环境。当我按下某个琴键会获得一些信息,如琴键的位置以及我的手的位置等等,这些构成了一个状态,同时我能听到该琴键的声音,这就是奖励(反馈),我通过这个琴键发出的声音判断我是否弹的好然后进行纠正。也可以参考下图(马尔科夫决策过程中智能体与环境的交互过程)来理解这个过程。
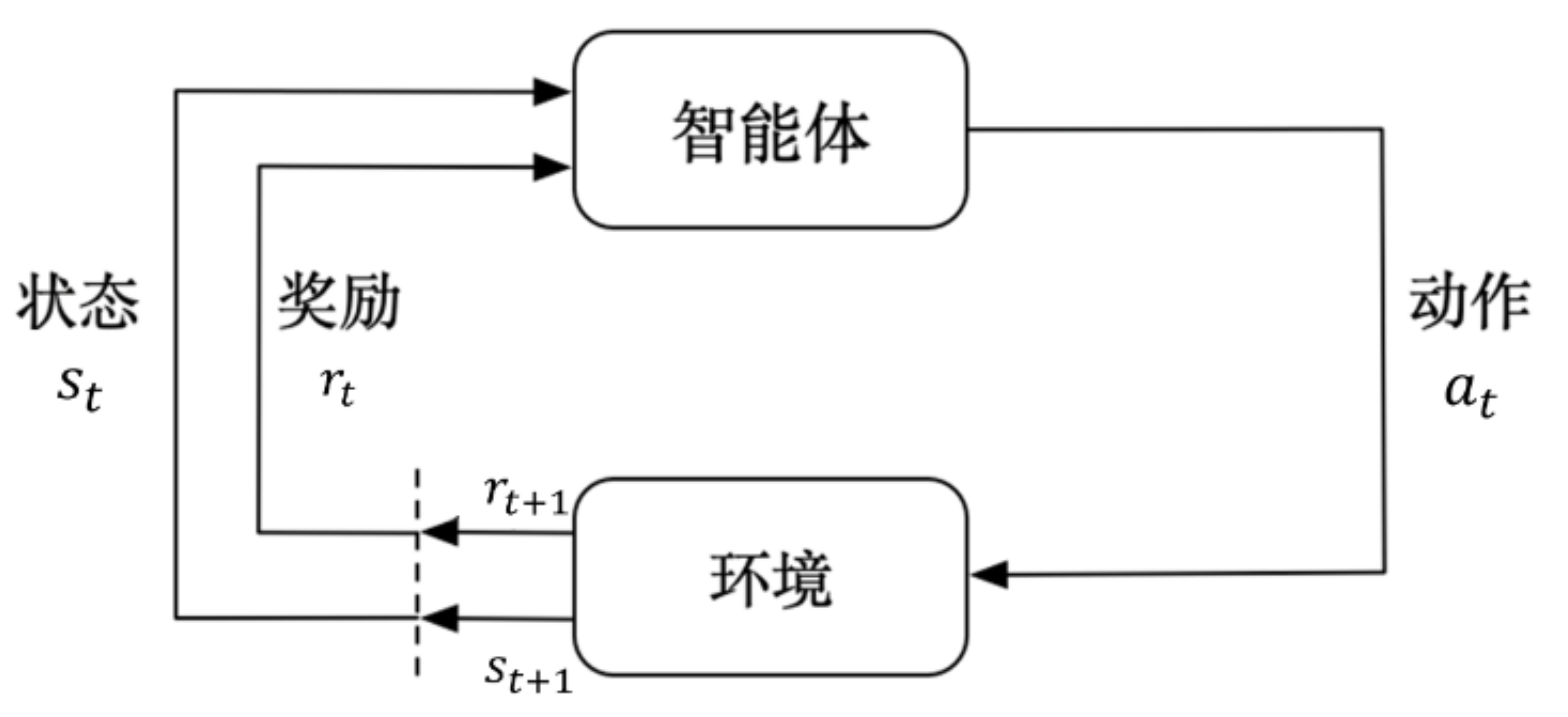
智能体与环境在一系列离散的时间戳交互,一般用\(t\)表示,\(t = 0,1,2 ···\)。在每个时间戳\(t\),智能体会观测当前环境下的状态\(s_{t}\),根据这个状态\(s_{t}\),做出一个决策\(a_{t}\),执行完该决策之后会获得一个奖励\(r_{t+1}\),同时环境收到智能体做出的这个决策后会被影响变成新的状态\(t_{t+1}\),并且在下一个时间戳\(t+1\)被智能体观测到,如此循环下去。其中奖励\(s_{t+1}\)就相当于弹钢琴时听到的声音,调子弹对了就表示正奖励,否则就是负奖励。此外,在强化学习中我们通常考虑的是有限马尔科夫决策过程,即\(t\)是有限的,上限一般用\(T\)表示,也就是当前交互过程的最后一个时间戳,从\(t=0\)到\(t=T\)这一段时间我们称为一个回合(episode),比如我们玩金铲铲,每一次英雄的更换或者装备的合成等等都是动作,但是一局的总轮数还是有限的,因此一整局就是一个回合episode。
这里的时间戳\(t=0\)和\(t=1\)与现实时间并无关系,取决于智能体每次交互获得反馈需要的时间。比如弹钢琴一旦按下去就马上能得到回馈(此时一个时间戳的间隔可能是0.1s),但是我们在锻炼肌肉的过程中并不会很快得到反馈(此时一个时间戳的间隔可能就是一个月)。
上述中的奖励表示为\(r_{t+1}\),而不是\(r_{t}\),原因是做出当前决策后才能获得奖励,因此更强调在下一个时间戳获得的奖励。
例3:扫地机器人可以通过简化变成MDP的一个简单示例。有限MARKOV决策过程提供了更多细节。(我们的目的是制作一个简单的例子,而不是一个特别现实的例子。)回想一下,智能体有时会根据外部事件(或机器人控制系统的其他部分)做出决定。每次这样的时候,机器人都会决定是否应该(1)主动寻找罐头,(2)保持静止,等待有人给它带来罐头,或者(3)回到基地给电池充电。假设环境的工作方式如下。找到罐头的最好方法是积极寻找,但这会耗尽机器人的电池,而等待则不会。每当机器人进行搜索时,其电池都有可能耗尽。在这种情况下,机器人必须关闭并等待救援(产生较低的奖励)。
智能体只根据电池的能量水平做出决定。它可以区分高和低两个级别,使得状态集为S={high,low}。让我们把可能的选择——智能体的行动——称为等待、搜索和充值。当能量水平很高时,充电总是愚蠢的,所以我们不将其包括在该状态的动作集中。智能体的动作集是
- 当能量水平为 high 时:\[\mathcal{A}(\mathtt{high}) = \{\mathtt{search}, \mathtt{wait}\} \]
- 当能量水平为 low 时:\[\mathcal{A}(\mathtt{low}) = \{\mathtt{search}, \mathtt{wait}, \mathtt{recharge}\} \]
如果能量水平很高,那么总是可以完成一段时间的主动搜索,而不会有耗尽电池的风险。从高能级开始的搜索周期使能级以概率\(α\)为高,并以概率\(1-α\)将其降低到低。另一方面,当能级较低时进行的一段时间的搜索使其以概率\(β\)变低,并以概率\(1-β\)耗尽电池。在后一种情况下,必须考虑机器人的能量剩余,然后将电池重新充电至高电位。每个收集的金属罐激励计为+1,每次重用的激励计为-3;记 \(r_{\mathtt{search}}\) 和 \(r_{\mathtt{wait}}\) 为搜寻和等待时金属罐的期望数,且假设 \(r_{\mathtt{search}} > r_{\mathtt{wait}}\),若设回去充电途中不会收集金属罐,这样这个系统就是一个有限MDP,其转移矩阵和期望激励为:
| \(s\) | $$s^{'}$$ | \(a\) | $$p(s^{'},s,a)$$ | $$r(s,a,s^{'})$$ |
|---|---|---|---|---|
| high | high | search | \(\alpha\) | \(r_{\text{search}}\) |
| high | low | search | \(1-\alpha\) | \(r_{\text{search}}\) |
| low | high | search | \(1-\beta\) | -3 |
| low | low | search | \(\beta\) | \(r_{\text{search}}\) |
| high | high | wait | 1 | \(r_{\text{wait}}\) |
| high | low | wait | 0 | \(r_{\text{wait}}\) |
| low | high | wait | 0 | \(r_{\text{wait}}\) |
| low | low | wait | 1 | \(r_{\text{wait}}\) |
| low | high | recharge | 1 | 0 |
| low | low | recharge | 0 | 0 |
1.1 MDP的性质
简单性和结构清晰:MDP由状态集、动作集、转移概率和奖励函数四个基本要素构成,结构简洁明了。这种简单性使得MDP易于理解和实现,成为研究和解决复杂决策问题的有效工具。
动态特性:MDP通过递归的贝尔曼方程动态更新和评估每个状态的价值,逐步逼近最优策略。动态规划算法如值迭代和策略迭代利用这种特性,通过反复迭代计算来优化决策过程。
可扩展性和灵活性:MDP能够扩展以处理更复杂的决策问题,如部分可观察马尔科夫决策过程(POMDP)。它可以适应各种环境和问题类型,从离散状态和动作的简单问题到连续状态和动作的复杂问题。
学习能力和优化:在强化学习中,MDP通过试错学习和经验积累不断改进决策策略。算法如Q学习、SARSA和深度Q网络(DQN)利用MDP框架,通过与环境的交互来学习最优策略,使系统在未知环境中自我改进。
理论完整性和可解释性:MDP具有坚实的数学基础,包括贝尔曼方程、动态规划和蒙特卡罗方法等。其决策过程透明且可解释,使决策者能够理解每个状态和动作的价值及其对最终结果的影响,这对于需要高可解释性的应用尤为重要。
1.2 MDP的应用场景
MDP在各个领域都有广泛的应用,以下是几个主要的应用场景:
机器人导航:在机器人导航中,机器人需要决定在每个时间步采取什么动作(如移动方向)以最大化到达目标位置的概率或最小化时间。
自动驾驶:自动驾驶车辆需要在复杂的交通环境中做出实时决策,以确保安全和效率。MDP可以帮助建模车辆在不同状态下的决策过程。
医疗决策:在医疗领域,MDP可以用于制定个性化的治疗方案,优化病人的治疗过程。
金融投资:投资者可以使用MDP模型来选择在不同市场状态下的投资策略,以最大化长期收益。
游戏AI:在游戏设计中,MDP可以用于开发具有智能行为的游戏角色,使其能够在游戏中做出最优决策。
二、马尔科夫决策过程的理论基础
MDP的理论基础主要包括以下几个方面:
马尔科夫性质:MDP假设系统的状态转移具有马尔科夫性质,即当前状态的转移只依赖于当前状态和当前动作,而与过去的状态和动作无关。这使得问题的复杂性大大降低,便于求解。
贝尔曼方程(Bellman Equation):贝尔曼方程是MDP的核心,用于描述最优策略的递归性质。具体来说,贝尔曼方程表示某个状态的值等于在该状态下采取最佳动作后获得的即时奖励加上转移到下一个状态后预期的长期奖励。数学表达如下:
$$V(s) = \max_{a \in A} \left[ R(s, a) + \gamma \sum_{s' \in S} P(s'|s,a) V(s') \right]$$其中,\(V(s)\) 是状态 \(s\) 的价值,\(R(s,a)\) 是在状态 \(s\) 采取动作 \(a\) 后的即时奖励,\(\gamma\) 是折扣因子,表示未来奖励的折现率,\(P(s′∣s,a)\) 是状态 \(s\) 在采取动作 \(a\) 后转移到状态 \(s'\) 的概率。Bellman方程是一个压缩映射,存在唯一的不动点 \(V^\star(s)\)。这就是价值迭代算法的收敛原理,对 $ V(s) $ 进行多次迭代后,会收敛到最优价值函数 $ V^\star(s) $。
动态规划(Dynamic Programming):动态规划是求解MDP的主要方法,包括值迭代(Value Iteration)和策略迭代(Policy Iteration)两种算法。这些算法利用贝尔曼方程,通过迭代更新状态值或策略,逐步逼近最优解。
马尔科夫决策过程是一个由5个元素组成的元祖\((S, A, P, R, \gamma)\)组成。MDP的目标是找到一个策略 \(\pi\),使得在该策略下,累积奖励期望最大化。策略 \(\pi\) 是状态到动作的映射,即 \(\pi(s) = a\)。为了量化策略的优劣,引入价值函数。价值函数可以分为状态价值函数 \(V(s)\) 和状态-动作价值函数 \(Q(s,a)\)。
- 状态价值函数 \(V(s)\)
状态价值函数 \(V^\pi(s)\) 表示在状态 \(s\) 下按照策略 \(\pi\) 行动时的累积奖励期望:
利用递归关系,状态价值函数可以表示为:
- 状态-动作价值函数 \(Q(s,a)\)
状态-动作价值函数 \(Q^\pi(s,a)\) 表示在状态 \(s\) 下执行动作 \(a\),并在后续按照策略 \(\pi\) 行动时的累积奖励期望:
同样地,利用递归关系,状态-动作价值函数可以表示为:
- 贝尔曼最优方程
在寻找最优策略 \(\pi^*\) 时,贝尔曼方程起到了关键作用。最优状态价值函数 \(V^*(s)\) 满足贝尔曼最优方程:
最优状态-动作价值函数 \(Q^*(s,a)\) 满足:
这些方程反映了当前状态和动作的价值不仅取决于即时奖励,还取决于未来状态的最大价值。
2.1 价值迭代算法
价值迭代是解决马尔科夫决策过程(MDP)的一种常用方法。它通过迭代更新状态价值函数\(V(s)\)来逐步逼近最优价值函数 \(V^*(s)\),从而找到最优策略 $ \pi^* $,具体算法如下。
-
初始化:
对于所有状态 \(s\in S\),初始化价值函数 \(V(s)\) 为任意值,通常选择0或随机值。 -
迭代更新:
直到价值函数收敛(即前后两次更新的差异小于预设的阈值 \(\theta\):
对于每个状态 $ s \in S $,执行以下更新:
$$ V_{k+1}(s) = \max_{a \in A} \sum_{s' \in S} P(s'|s, a) \left[ R(s, a, s') + \gamma V_k(s') \right] $$ -
确定最优策略:
根据收敛后的价值函数 \(V^*(s)\),为每个状态 \(s \in S\)确定最优动作 $ a^* $:\[\pi^*(s) = \arg\max_{a \in A} \sum_{s' \in S} P(s'|s, a) \left[ R(s, a, s') + \gamma V^*(s') \right] \]
2.2 策略迭代算法
策略迭代是求解马尔科夫决策过程(MDP)的一种方法,它通过交替进行策略评估和策略改进,逐步逼近最优策略 \(\pi^*\),算法步骤如下。
-
初始化:
随机初始化一个策略 $ \pi$ -
策略评估:
计算当前策略\(\pi\)下的状态价值函数$ V^\pi(s) $。
通过解线性方程组求解:
$$ V^\pi(s) = \sum_{a \in A} \pi(a|s) \sum_{s' \in S} P(s'|s, a) \left[ R(s, a, s') + \gamma V^\pi(s') \right] $$ -
策略改进:
使用新的状态价值函数 \(V^\pi(s)\)更新策略\(\pi\):
$$ \pi'(s) = \arg\max_{a \in A} \sum_{s' \in S} P(s'|s, a) \left[ R(s, a, s') + \gamma V^\pi(s') \right] $$ -
重复:
如果策略$\pi $ 不再改变(即 $\pi' = \pi $,则停止,否则设置 $ \pi = \pi' $并返回第2步。
2.3 线性规划算法
线性规划(Linear Programming, LP)是一种优化技术,可以用于求解马尔科夫决策过程(MDP)的最优策略。线性规划方法通过构建线性方程组,直接求解最优状态价值函数或最优策略,通过线性规划求解MDP的目标是找到最优状态价值函数\(V^*(s)\)。我们可以将求解MDP的过程转化为一个线性规划问题:
三、实例展示
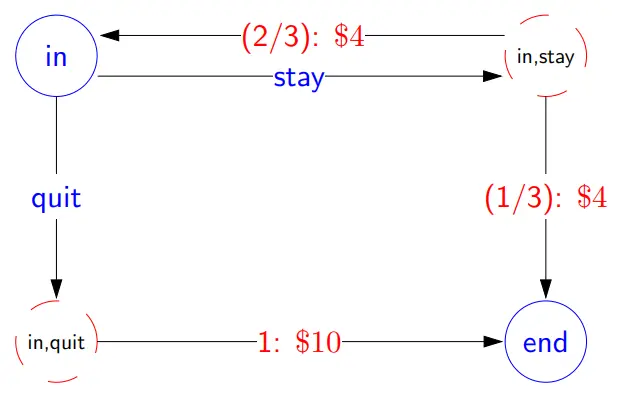
现在玩一个骰子游戏,你有两个选择,摇骰子或退出,如果选择退出,你就能直接获得 10,游戏结束。如果摇骰子你可以获得 4。但如果摇到了 1 或 2,则游戏结束。如果是其他的,那么你便可以继续游戏下一轮的游戏。
| 状态转移图 | 关系转化 |
|---|---|
 |
 |
- 转移概率和奖励
游戏中有两种状态:in 或 end。在 in 状态下,有两种动作:stay 或 quit。如果选择 quit,转移概率为 1,获得奖励 10;如果选择 stay,有 2/3 的概率继续 in 状态,获得奖励 4;有 1/3 的概率结束游戏,获得奖励 4。转移概率表如下:
| \(s\) | \(a\) | \(s^{'}\) | $$T(s,a,s^{'})$$ | $$r(s,a,s^{'})$$ |
|---|---|---|---|---|
| in | quit | end | 1 | $10 |
| in | stay | in | 2/3 | $4 |
| in | stay | end | 1/3 | $4 |
转移概率公式\(T(s'|s,a)\);概率性质:\(\sum_{s' \in states} T(s'|s,a) = 1\);奖励公式:$ R(s'|s,a)$
- 策略和效用
策略 (policy) \(\pi\):指导在每个状态下应采取的动作;效用 (utility):策略产生的收益总和。
例如,连续选择 3 次 stay 结束游戏,效用为:$ u_1 = 3 \times 4 = 12 $。考虑时间成本,引入折扣系数 (discount factor) \(\gamma ,0 ≤ γ ≤ 1\)。
效用公式变为:$$u = r_1 + \gamma r_2 + \gamma^2 r_3 + \gamma^3 r_4 + ... $$
例如,$ \gamma = 0.8 $,连续选择 3 次 stay,效用为:
- 策略评估
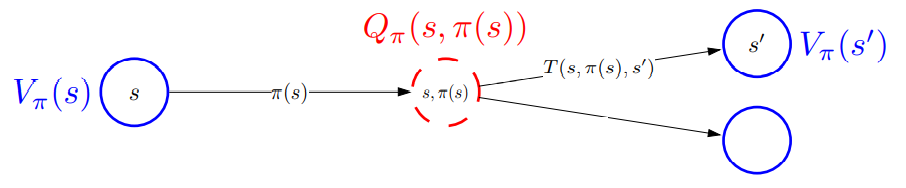
状态值 (V值) $V_{\pi}(s) $:遵循策略 $ \pi $ 在状态 s 下的预期效用。
状态-动作值 (Q值) $ Q_{\pi}(s,a) $:从状态 s 采取行动 a,然后遵循策略 \(\pi\) 的预期效用。
贝尔曼期望函数 Bellman Expectation Equation:
- 计算V值和Q值
使用迭代方法计算给定策略的V值和Q值,直到收敛于一定误差范围。先随便指定策略的V值和Q值,然后通过一遍遍的重复策略获得奖励值,直到V值和Q值收敛于一定误差范围。
四、Python实现
#价值迭代算法
def value_iteration(S, A, P, R, gamma, theta):
V = {s: 0 for s in S} # 初始化价值函数
while True:
delta = 0
for s in S:
v = V[s]
V[s] = max(sum(P(s_prime, s, a) * (R(s, a, s_prime) + gamma * V[s_prime]) for s_prime in S) for a in A)
delta = max(delta, abs(v - V[s]))
if delta < theta:
break
policy = {}
for s in S:
policy[s] = max(A, key=lambda a: sum(P(s_prime, s, a) * (R(s, a, s_prime) + gamma * V[s_prime]) for s_prime in S))
return V, policy
# 定义MDP元素
S = ['in', 'end']
A = ['stay', 'quit']
gamma = 0.5 # 定义折扣因子
theta = 0.0001 # 收敛阈值
def P(s_prime, s, a):
if s == 'in' and a == 'stay':
return 2/3 if s_prime == 'in' else 1/3
elif s == 'in' and a == 'quit':
return 1 if s_prime == 'end' else 0
elif s == 'end':
return 0
return 0
def R(s, a, s_prime):
if s == 'in' and a == 'stay':
return 4
elif s == 'in' and a == 'quit' and s_prime == 'end':
return 10
return 0
V, policy = value_iteration(S, A, P, R, gamma, theta)
print("Value Iteration - 最优价值函数:", V)
print("Value Iteration - 最优策略:", policy)
#策略迭代算法
# 定义MDP元素
S = ['in', 'end']
A = ['stay', 'quit']
gamma = 0.5 # 定义折扣因子
theta = 0.0001 # 收敛阈值
def P(s_prime, s, a):
if s == 'in' and a == 'stay':
return 2/3 if s_prime == 'in' else 1/3
elif s == 'in' and a == 'quit':
return 1 if s_prime == 'end' else 0
elif s == 'end':
return 0
return 0
def R(s, a, s_prime):
if s == 'in' and a == 'stay':
return 4
elif s == 'in' and a == 'quit' and s_prime == 'end':
return 10
return 0
def policy_iteration(S, A, P, R, gamma, theta):
policy = {s: A[0] for s in S} # 初始化策略
while True:
V = {s: 0 for s in S}
while True:
delta = 0
for s in S:
v = V[s]
V[s] = sum(P(s_prime, s, policy[s]) * (R(s, policy[s], s_prime) + gamma * V[s_prime]) for s_prime in S)
delta = max(delta, abs(v - V[s]))
if delta < theta:
break
policy_stable = True
for s in S:
old_action = policy[s]
policy[s] = max(A, key=lambda a: sum(P(s_prime, s, a) * (R(s, a, s_prime) + gamma * V[s_prime]) for s_prime in S))
if old_action != policy[s]:
policy_stable = False
if policy_stable:
return V, policy
# 运行策略迭代算法
V_pi, policy_pi = policy_iteration(S, A, P, R, gamma, theta)
# 打印结果
print("Policy Iteration - 最优价值函数:")
for state in V_pi:
print(f" 状态 {state}: {V_pi[state]}")
print("Policy Iteration - 最优策略:")
for state in policy_pi:
print(f" 状态 {state}: 选择动作 {policy_pi[state]}")
#线性规划算法
import numpy as np
from scipy.optimize import linprog
# 定义MDP元素
S = ['in', 'end']
A = ['stay', 'quit']
gamma = 0.5 # 定义折扣因子
def P(s_prime, s, a):
if s == 'in' and a == 'stay':
return 2/3 if s_prime == 'in' else 1/3
elif s == 'in' and a == 'quit':
return 1 if s_prime == 'end' else 0
elif s == 'end':
return 0
return 0
def R(s, a, s_prime):
if s == 'in' and a == 'stay':
return 4
elif s == 'in' and a == 'quit' and s_prime == 'end':
return 10
return 0
def mdp_linear_programming(S, A, P, R, gamma):
c = np.ones(len(S))
A_ub = []
b_ub = []
state_index = {s: i for i, s in enumerate(S)}
for s in S:
for a in A:
constraint = np.zeros(len(S))
constraint[state_index[s]] = -1
for s_prime in S:
constraint[state_index[s_prime]] += P(s_prime, s, a) * gamma
A_ub.append(constraint)
b_ub.append(-sum(P(s_prime, s, a) * R(s, a, s_prime) for s_prime in S))
A_ub = np.array(A_ub)
b_ub = np.array(b_ub)
res = linprog(c, A_ub=A_ub, b_ub=b_ub, method='highs')
if res.success:
V = res.x
policy = {s: max(A, key=lambda a: sum(P(s_prime, s, a) * (R(s, a, s_prime) + gamma * V[state_index[s_prime]]) for s_prime in S)) for s in S}
return V, policy
else:
raise ValueError("Linear programming failed to find a solution")
V_lp, policy_lp = mdp_linear_programming(S, A, P, R, gamma)
print("Linear Programming - 最优价值函数:")
for i, state in enumerate(S):
print(f" 状态 {state}: {V_lp[i]}")
print("Linear Programming - 最优策略:")
for state in policy_lp:
print(f" 状态 {state}: 选择动作 {policy_lp[state]}")
Value Iteration - 最优价值函数: {'in': 10.0, 'end': 0.0}
Value Iteration - 最优策略: {'in': 'quit', 'end': 'stay'}
Policy Iteration - 最优价值函数: {'in': 10.0, 'end': 0.0}
Policy Iteration - 最优策略: {'in': 'quit', 'end': 'stay'}
Linear Programming - 最优价值函数: [10. 0.]
Linear Programming - 最优策略: {'in': 'quit', 'end': 'stay'}
import numpy as np
# 定义MDP元素
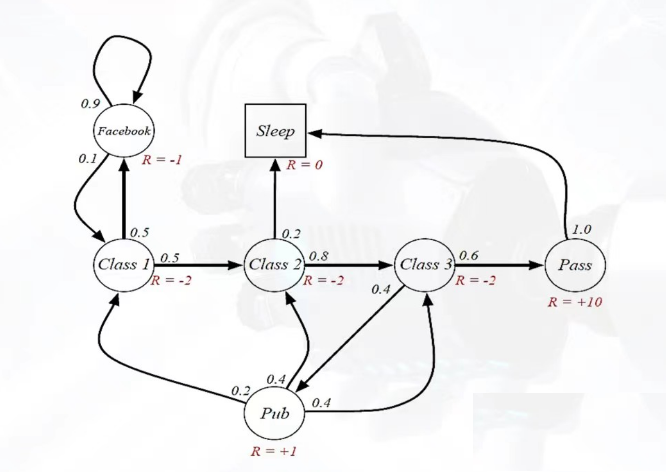
S = ['Facebook', 'Class1', 'Class2', 'Class3', 'Sleep', 'Pub', 'Pass']
A = {
'Facebook': ['Facebook'],
'Class1': ['Class1', 'Pub'],
'Class2': ['Class2', 'Sleep'],
'Class3': ['Class3', 'Pass'],
'Sleep': [],
'Pub': ['Pub', 'Class2'],
'Pass': []
}
gamma = 0.8 # 折扣因子
theta = 0.0001 # 收敛阈值
# 转移概率和奖励函数
def P(s_prime, s, a):
if s == 'Facebook' and a == 'Facebook':
return 0.9 if s_prime == 'Facebook' else 0.1 if s_prime == 'Class1' else 0
elif s == 'Class1' and a == 'Class1':
return 0.5 if s_prime == 'Class1' else 0.5 if s_prime == 'Class2' else 0
elif s == 'Class1' and a == 'Pub':
return 0.2 if s_prime == 'Pub' else 0.4 if s_prime == 'Class2' else 0.4 if s_prime == 'Class3' else 0
elif s == 'Class2' and a == 'Class2':
return 0.2 if s_prime == 'Class2' else 0.8 if s_prime == 'Class3' else 0
elif s == 'Class2' and a == 'Sleep':
return 1 if s_prime == 'Sleep' else 0
elif s == 'Class3' and a == 'Class3':
return 0.4 if s_prime == 'Pub' else 0.6 if s_prime == 'Pass' else 0
elif s == 'Pub' and a == 'Pub':
return 1 if s_prime == 'Pub' else 0
elif s == 'Pub' and a == 'Class2':
return 1 if s_prime == 'Class2' else 0
return 0
def R(s, a, s_prime):
if s == 'Facebook' and a == 'Facebook':
return -1
elif s == 'Class1' and a == 'Class1':
return -2
elif s == 'Class1' and a == 'Pub':
return 1 if s_prime == 'Pub' else -2 if s_prime == 'Class2' else 0
elif s == 'Class2' and a == 'Class2':
return -2
elif s == 'Class2' and a == 'Sleep':
return 0
elif s == 'Class3' and a == 'Class3':
return -2
elif s == 'Class3' and a == 'Pass':
return 10
elif s == 'Pub' and a == 'Pub':
return 1
elif s == 'Pub' and a == 'Class2':
return -2
return 0
def value_iteration(S, A, P, R, gamma, theta):
V = {s: 0 for s in S} # 初始化价值函数
while True:
delta = 0
for s in S:
if not A[s]: # 没有可选动作
continue
v = V[s]
V[s] = max(sum(P(s_prime, s, a) * (R(s, a, s_prime) + gamma * V[s_prime]) for s_prime in S) for a in A[s])
delta = max(delta, abs(v - V[s]))
if delta < theta:
break
policy = {}
for s in S:
if not A[s]: # 没有可选动作
continue
policy[s] = max(A[s], key=lambda a: sum(P(s_prime, s, a) * (R(s, a, s_prime) + gamma * V[s_prime]) for s_prime in S))
return V, policy
V_vi, policy_vi = value_iteration(S, A, P, R, gamma, theta)
# 输出结果,保留两位小数
V_vi = {k: round(v, 2) for k, v in V_vi.items()}
print("价值迭代 - 最优价值函数:", V_vi)
print("价值迭代 - 最优策略:", policy_vi)
价值迭代 - 最优价值函数: {'Facebook': -3.51, 'Class1': 0.2, 'Class2': 0.0, 'Class3': 0.0, 'Sleep': 0, 'Pub': 5.0, 'Pass': 0}
价值迭代 - 最优策略: {'Facebook': 'Facebook', 'Class1': 'Pub', 'Class2': 'Sleep', 'Class3': 'Pass', 'Pub': 'Pub'}
总结
马尔科夫决策过程是一个强大的工具,用于建模和解决不确定环境下的序列决策问题。它通过定义状态、动作、转移概率和奖励函数,提供了一个系统化的方法来找到最优策略。MDP在许多领域都有广泛应用,从机器人导航到金融投资,从医疗决策到游戏AI,其理论基础包括马尔科夫性质、贝尔曼方程和动态规划等。此外,强化学习作为MDP的扩展方法,使得我们能够在未知环境中通过经验学习到最优策略。马尔科夫决策过程不仅提供了一个理论框架,还为实践中的复杂决策问题提供了有效的解决方案。随着计算能力和算法的不断发展,MDP及其相关技术将在更多领域中发挥更大的作用。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号