K-means聚类思想及其Python实现
聚类就是将一个庞杂数据集中具有相似特征的数据自动归类到一起,称为一个簇,簇内的对象越相似,聚类的效果越好。“相似”这一概念,是利用距离标准来衡量的,我们通过计算对象与对象之间的距离远近来判断它们是否属于同一类别,即是否是同一个簇。聚类是一种无监督的学习(Unsupervised Learning)方法,不需要预先标注好的训练集。聚类与分类最大的区别就是分类的目标事先已知,对于一个动物集来说,你并不清楚这个数据集内部有多少种类的动物,你能做的只是利用聚类方法将它自动按照特征分为多类,然后人为给出这个聚类结果的定义(即簇识别)。例如,你将一个动物集分为了三簇(类),然后通过观察这三类动物的特征,你为每一个簇起一个名字,如大象、狗、猫等,这就是聚类的基本思想。k-means就是一个聚类的算法,属于无监督学习算法,也是就样本没有label(标签),然后根据某种规则进行“分割”,把相同的或者相近的放在一起。K-means算法的基本思想是通过不断更新簇的中心点,将数据集划分为预定数量的簇。这一过程涉及到计算数据点之间的距离,通常使用欧式距离作为相似性度量。在算法执行过程中,每个数据点被分配到距离最近的簇,然后更新簇的中心,迭代进行直至收敛。
| 蚂群 | 狼群 |
|---|---|
 |
 |
一、K-means算法的发展和思想
1.1 K-means算法发展
K-means算法是一种经典的聚类算法,它于1957年由J.B. MacQueen首次提出。该算法的主要目标是将数据集分成k个簇,使得每个数据点都属于离其最近的簇。K-means的发展经历了几个阶段,不断在性能和应用方面进行改进。
初始提出阶段:K-means最初是在统计学领域提出的,用于解决聚类问题。J.B. MacQueen于1967年将其描述为一种迭代优化算法,通过最小化簇内平方和来确定聚类的中心点。该方法在处理大型数据集时效率较高,成为了早期聚类算法的代表。
算法优化阶段:随着计算机技术的进步,K-means算法得以更广泛的应用。研究者们开始关注算法的性能和效率,提出了一些优化方法。其中最著名的是Lloyd's算法,该算法通过交替迭代更新簇中心和分配数据点,加速了K-means的收敛过程。此外,还有一些采用随机化初始化的改进方法,以避免算法陷入局部最小值。
高性能计算和大规模数据处理阶段:随着计算机硬件和软件技术的飞速发展,K-means算法得以处理更大规模的数据集。并行化和分布式计算成为改进算法性能的关键。研究者们提出了一些并行K-means和分布式K-means的变体,以应对大规模数据的挑战。
对异常值和噪声的鲁棒性改进:K-means算法对初始聚类中心敏感,容易受到异常值和噪声的影响。为了提高算法的鲁棒性,研究者们引入了一些对异常值不敏感的改进方法,如K-medoids算法,该算法使用簇内中心点的中位数而不是均值。
融合其他技术的发展:随着深度学习等新技术的崛起,研究者们开始探索将K-means与其他技术融合,以提高聚类的效果。例如,K-means和自编码器相结合的深度聚类方法,通过学习数据的高阶表示来改善聚类效果。
总体而言,K-means算法从提出至今经历了多个阶段的发展,不断在算法性能、处理规模和鲁棒性方面进行改进。它在数据挖掘、图像分割、无监督学习等领域得到广泛应用,成为了一种经典而实用的聚类算法。
1.2 K-Means算法思想
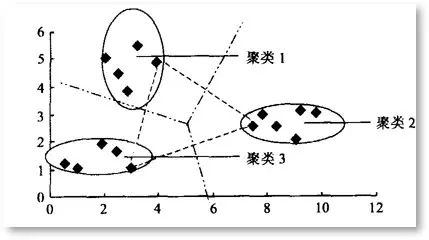
基于相似性度量,使得相同子集中各元素间差异性最小,而不同子集间的元素差异性最大,这就是(空间)聚类算法的本质,K-Means正是这样一种算法的代表。K-Means聚类被提出已经超过50年,但仍然是应用最广泛、地位最核心的空间数据划分聚类方法之一。作为一种无监督算法,尽管无法判断结果对错,但是它将为我们研究对象群体的内部结构提供一些很好的切入点。K-means算法算法的输入为一个样本集(或者称为点集),通过该算法可以将样本进行聚类,具有相似特征的样本聚为一类。针对每个点,计算这个点距离所有中心点最近的那个中心点,然后将这个点归为这个中心点代表的簇。一次迭代结束之后,针对每个簇类,重新计算中心点,然后针对每个点,重新寻找距离自己最近的中心点。如此循环,直到前后两次迭代的簇类没有变化。
| 图1 | 图2 |
|---|---|
 |
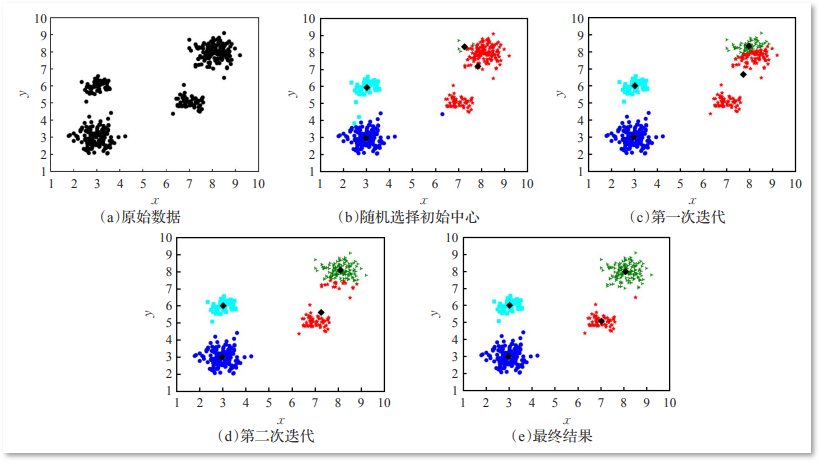 |
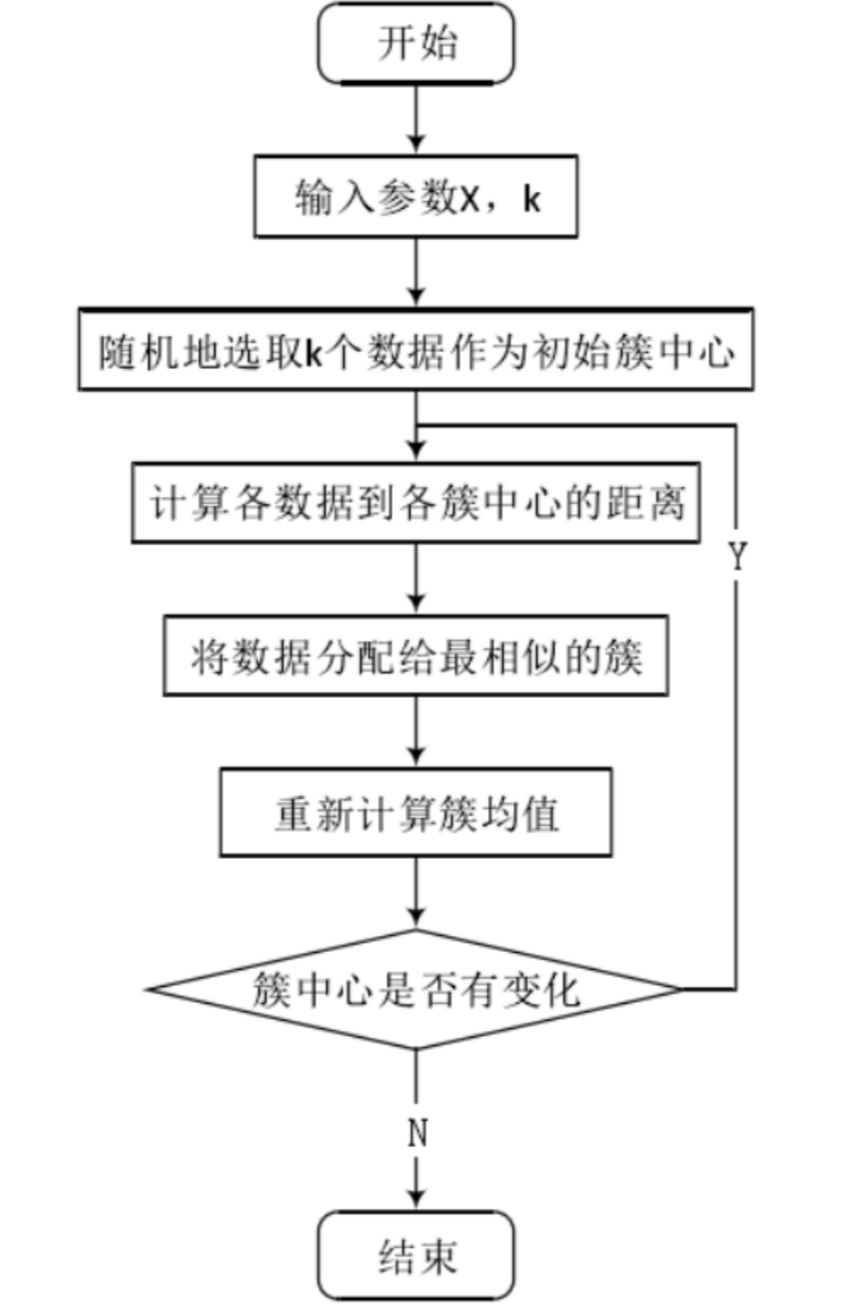
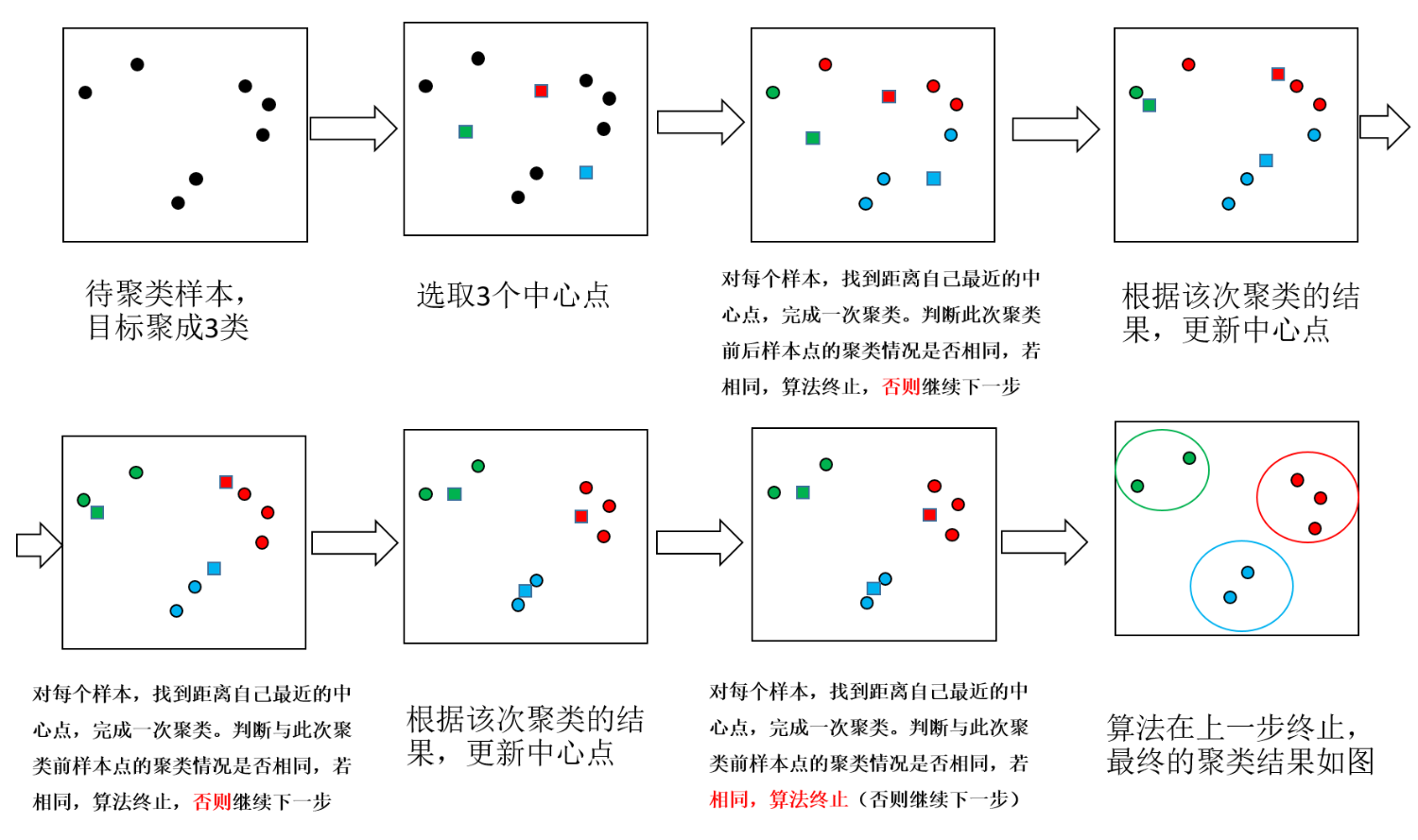
K-means(K均值)算法接受一个参数K用以决定结果中簇的数目。算法开始时,要在数据集中随机选择K个数据对象用来当做k个簇的初始中心,而将剩下的各个数据对象就根据他们和每个聚类簇心的距离选择簇心最近的簇分配到其中。然后重新计算各个聚类簇中的所有数据对象的平均值,并将得到的结果作为新的簇心;逐步重复上述的过程直至目标函数收敛为止。其步骤具体地:
STEP1: 从N个样本数据中随机选取K个对象,作为初始的聚类中心;
STEP2: 分别计算每个样本点到各个聚类中心的距离,并逐个分配到距离其最近的簇中;
STEP3: 所有对象分配完成后,更新K个类中心位置,类中心定义为簇内所有对象在各个维度的均值;
STEP4: 与前一次计算得到的K个聚类中心比较,如果聚类中心发生变化,转至步骤2,否则转至步骤5;
STEP5: 当类中心不再发生变化,停止并输出聚类结果,然后整理我们所需要的信息,如各个样本所属的类等等,进行后续的统计和分析。
聚类结束之前,类中心会不断移动,而随着类中心的移动,样本的划分情况也会持续发生改变。
1.3 K-means算法的优缺点
K-means算法具有一些明显的优点和缺点。
优点:
简单且高效: K-means算法实现简单,易于理解和部署,对于大规模数据集具有较高的计算效率。
可扩展性: 随着计算机硬件和软件技术的进步,K-means算法能够处理大规模数据集,并且可以通过并行计算和分布式计算进一步提高可扩展性。
广泛应用: K-means在许多领域得到广泛应用,包括数据挖掘、图像分割、无监督学习等,是一种通用且灵活的聚类算法。
缺点:
对初始聚类中心敏感: K-means对初始聚类中心的选择敏感,不同的初始点可能导致不同的聚类结果,因此需要采用一些启发式方法或多次运行以选择最优结果。
假设簇为凸形: K-means假设簇为凸形,对于不规则形状的簇效果较差,容易产生误差。
不适用于非球形簇: 由于K-means使用欧氏距离作为相似性度量,因此对于非球形簇的数据集效果较差,可能导致聚类失真。
无法处理噪声和异常值: K-means对噪声和异常值敏感,可能影响聚类结果的准确性,尤其是在存在离群点的情况下。
综合而言,K-means算法在处理大规模、简单结构的数据集上表现优越,但在处理复杂、非凸形状或含有噪声的数据集时存在一些限制。在选择使用K-means时,需要根据具体应用场景权衡其优缺点。
二、K-means方法算例
| 图3 | 图4 |
|---|---|
 |
 |
假设有如下8个点:(3,1),(3,2),(4,1),(4,2),(1,3),(1,4),(2,3),(2,4)。使用K-means算法对其进行聚类。设初始聚类中心分别为(0,4)和(3,3)。请写出详细的计算过程。
- 原始数据
| X | Y | |
| A1 | 3 | 1 |
| A2 | 3 | 2 |
| A3 | 4 | 1 |
| A4 | 4 | 2 |
| A5 | 1 | 3 |
| A6 | 1 | 4 |
| A7 | 2 | 3 |
| A8 | 2 | 4 |
- 初始聚类中心分别为D1(0,4)和D2(3,3),计算各点到两中心的距离。
| D1(0,4) | D2(3,3) | |
| A1(3,1) | 4.242 | 2 √ |
| A2(3,2) | 3.605 | 1 √ |
| A3(4,1) | 5 | 2.236 √ |
| A4(4,2) | 4.472 | 1.414 √ |
| A5(1,3) | 1.414 √ | 2 |
| A6(1,4) | 1 √ | 2.236 |
| A7(2,3) | 2.236 | 1 √ |
| A8(2,4) | 2 | 1.414 √ |
- 根据上表可分成两簇,{A1,A2,A3,A4,A7,A8},{A5,A6}。重新计算新的聚类中心D3,D4。并计算新的距离表。
D3=(3+3+4+4+2+2)/6,(1+2+1+2+3+4)/6 = (3,2.167)
D4=(1+1)/2,(3+4)/2 = (1,3.5)
| D3(3, 2.167) | D4(1,3.5) | |
| A1(3,1) | 1.167 √ | 3.201 |
| A2(3,2) | 0.167 √ | 2,5 |
| A3(4,1) | 1.536 √ | 3.905 |
| A4(4,2) | 1.013 √ | 3.354 |
| A5(1,3) | 2.166 | 0.5 √ |
| A6(1,4) | 2.712 | 0.5 √ |
| A7(2,3) | 1.301 | 1.118 √ |
| A8(2,4) | 2.088 | 1.118 √ |
- 根据上表分成两簇,{A1,A2,A3,A4},{A5,A6,A7,A8}。重新计算新的聚类中心D5,D6。并计算新的距离表。
D5=(3+3+4+4)/4,(1+2+1+2)/4 = (3.5,1.5)
D6=(1+1+2+2)/4,(3+4+3+4)/4 = (1.5,3.5)
| D5(3.5,1.5) | D6(1.5,3.5) | |
| A1(3,1) | 0.707 √ | 2.915 |
| A2(3,2) | 0.707 √ | 2.121 |
| A3(4,1) | 0.707 √ | 3.535 |
| A4(4,2) | 0.707 √ | 2.915 |
| A5(1,3) | 2.915 | 0.707 √ |
| A6(1,4) | 3.535 | 0.707 √ |
| A7(2,3) | 2.121 | 0.707 √ |
| A8(2,4) | 2.915 | 0.707 √ |
- 根据上表分成两簇,{A1,A2,A3,A4},{A5,A6,A7,A8},和前述分簇一致,停止计算。
import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
# 创建数据框,包含所有列
data = {
'ID': ['A1', 'A2', 'A3', 'A4', 'A5', 'A6', 'A7', 'A8'],
'X': [3, 3, 4, 4, 1, 1, 2, 2],
'Y': [1, 2, 1, 2, 3, 4, 3, 4]
}
df = pd.DataFrame(data)
# 定义K-means模型,其中k=2
kmeans = KMeans(n_clusters=2, random_state=0)
# 对数据进行拟合并获取聚类标签
labels = kmeans.fit_predict(df[['X', 'Y']])
# 将聚类标签添加到数据框中
df['Cluster'] = labels
# 打印带有聚类标签的数据框
print(df)
# 可视化结果
plt.scatter(df['X'], df['Y'], c=df['Cluster'], cmap='viridis')
# 为每个数据点添加标签(使用行名)
for i, txt in enumerate(df['ID']):
plt.annotate(txt, (df['X'][i], df['Y'][i]))
# 绘制集群中心点
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='black', s=200, alpha=0.5, label='Centroids')
# 添加图例
plt.legend()
# 添加坐标轴标签和标题
plt.xlabel('X')
plt.ylabel('Y')
plt.title('K-means Clustering with Data Point Labels')
# 显示图形
plt.show()
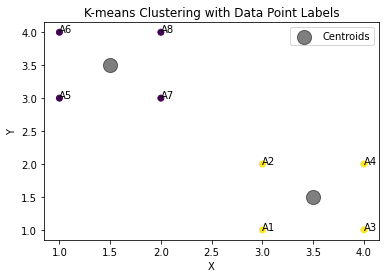
三、Python程序
数据文件下载https://github.com/helloWorldchn/MachineLearning
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
from sklearn.metrics import f1_score, accuracy_score, normalized_mutual_info_score, rand_score
from sklearn.preprocessing import LabelEncoder
from sklearn.decomposition import PCA
# 数据保存在.csv文件中
iris = pd.read_csv("dataset/Iris.csv", header=0) # 鸢尾花数据集 Iris class=3
wine = pd.read_csv("dataset/wine.csv") # 葡萄酒数据集 Wine class=3
seeds = pd.read_csv("dataset/seeds.csv") # 小麦种子数据集 seeds class=3
wdbc = pd.read_csv("dataset/wdbc.csv") # 威斯康星州乳腺癌数据集 Breast Cancer Wisconsin (Diagnostic) class=2
glass = pd.read_csv("dataset/glass.csv") # 玻璃辨识数据集 Glass Identification class=6
df = iris # 设置要读取的数据集
# print(df)
columns = list(df.columns) # 获取数据集的第一行,第一行通常为特征名,所以先取出
features = columns[:len(columns) - 1] # 数据集的特征名(去除了最后一列,因为最后一列存放的是标签,不是数据)
dataset = df[features] # 预处理之后的数据,去除掉了第一行的数据(因为其为特征名,如果数据第一行不是特征名,可跳过这一步)
attributes = len(df.columns) - 1 # 属性数量(数据集维度)
class_labels = list(df[columns[-1]]) # 原始标签
k = 3
# 这里已经知道了分3类,其他分类这里的参数需要调试
model = KMeans(n_clusters=k)
# 训练模型
model.fit(dataset)
# 预测全部数据
label = model.predict(dataset)
print(label)
def clustering_indicators(labels_true, labels_pred):
if type(labels_true[0]) != int:
labels_true = LabelEncoder().fit_transform(df[columns[len(columns) - 1]]) # 如果数据集的标签为文本类型,把文本标签转换为数字标签
f_measure = f1_score(labels_true, labels_pred, average='macro') # F值
accuracy = accuracy_score(labels_true, labels_pred) # ACC
normalized_mutual_information = normalized_mutual_info_score(labels_true, labels_pred) # NMI
rand_index = rand_score(labels_true, labels_pred) # RI
return f_measure, accuracy, normalized_mutual_information, rand_index
F_measure, ACC, NMI, RI = clustering_indicators(class_labels, label)
print("F_measure:", F_measure, "ACC:", ACC, "NMI", NMI, "RI", RI)
if attributes > 2:
dataset = PCA(n_components=2).fit_transform(dataset) # 如果属性数量大于2,降维
# 打印出聚类散点图
plt.scatter(dataset[:, 0], dataset[:, 1], marker='o', c='black', s=7) # 原图
plt.show()
colors = np.array(["red", "blue", "green", "orange", "purple", "cyan", "magenta", "beige", "hotpink", "#88c999"])
# 循换打印k个簇,每个簇使用不同的颜色
for i in range(k):
plt.scatter(dataset[np.nonzero(label == i), 0], dataset[np.nonzero(label == i), 1], c=colors[i], s=7)
plt.show()
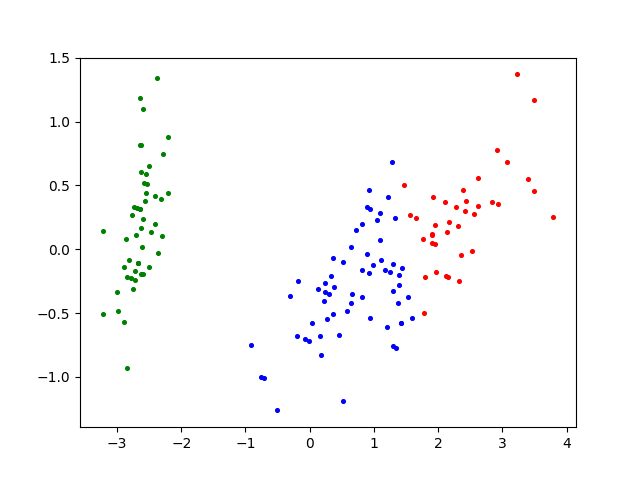
四、\(k\)值的选择
k-means算法因为手动选取k值和初始化随机质心的缘故,每一次的结果不会完全一样,而且由于手动选取k值,我们需要知道我们选取的k值是否合理,聚类效果好不好,那么如何来评价某一次的聚类效果呢?也许将它们画在图上直接观察是最好的办法,但现实是,我们的数据不会仅仅只有两个特征,一般来说都有十几个特征,而观察十几维的空间对我们来说是一个无法完成的任务。因此,我们需要一个公式来帮助我们判断聚类的性能,这个公式就是SSE (Sum of Squared Error, 误差平方和 ),它其实就是每一个点到其簇内质心的距离的平方值的总和,这个数值对应kmeans函数中clusterAssment矩阵的第一列之和。 SSE值越小表示数据点越接近于它们的质心,聚类效果也越好。 因为对误差取了平方,因此更加重视那些远离中心的点。一种肯定可以降低SSE值的方法是增加簇的个数,但这违背了聚类的目标。聚类的目标是在保持簇数目不变的情况下提高簇的质量。
4.1 惯性指标(inertia)
在K-means聚类时我们需要找到簇的数量,有一个惯性指标。k-Means的惯性计算方式是,每个样本与最接近的集群中心点的均方距离的总和。通常会得到一条类似于人的肘部的曲线。
给定一个包含 \(n\) 个数据对象的数据集合 \(D=\left\{x_1, x_2, \cdots, x_n\right\}\) ,定义经由 K-means 算法进行聚类后产生的类别集合为集合 \(C=\left\{C_1, C_2, \cdots, C_K\right\}\) ,则 SSE 的公式如下:
其中 \(m_k\) 是簇 \(C_k\) 的中心点,计算方法如下所示:
该方法选择的并不是误差平方和最小的\(k\),而是误差平方和突然变小时对应的\(k\)值。见下图所示,SSE的值会迅速下降,在\(k=6\)的时候达到一个肘点。在此之后,代价函数的值会就下降得非常慢,所以,我们选择\(k=6\),这个方法叫“肘部法则” 。
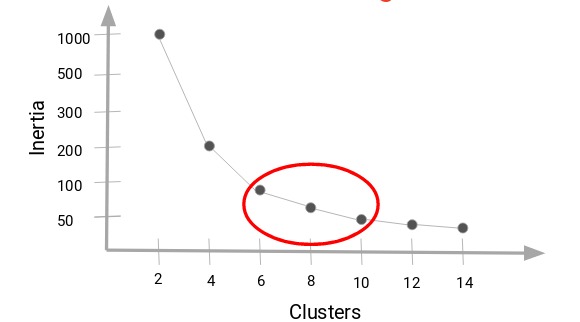
这是因为在确定聚类簇数时,还必须考虑计算成本。如果我们增加聚类的数量,计算成本也会增加。K-means算法还存在一个问题,它有可能会停留在一个局部最小值处,而这取决于初始化的情况。为了解决这个问题,我们通常需要多次运行K-means算法,每一次都重新进行随机初始化,最后再比较多次运行K-means的结果,选择代价函数最小的结果。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
# 提供的数据
data = {
'ID': ['A1', 'A2', 'A3', 'A4', 'A5', 'A6', 'A7', 'A8'],
'X': [3, 3, 4, 4, 1, 1, 2, 2],
'Y': [1, 2, 1, 2, 3, 4, 3, 4]
}
# 创建DataFrame
df = pd.DataFrame(data)
# 提取用于聚类的特征
X = df[['X', 'Y']] # 注意修正这里的语法错误
# 初始化KMeans模型列表,并设定k的范围
range_n_clusters = [1, 2, 3, 4, 5, 6, 7, 8] # 扩大了k的范围
inertia_scores = []
# 对每个k值进行聚类并计算惯性指标
for n_clusters in range_n_clusters:
# 使用KMeans算法
kmeans = KMeans(n_clusters=n_clusters, random_state=42)
kmeans.fit(X)
# 获取惯性指标
inertia = kmeans.inertia_
inertia_scores.append(inertia)
# 绘制惯性指标随聚类数量变化的图形
plt.figure(figsize=(10, 4)) # 扩大了图形尺寸以便更好地显示更多点
plt.plot(range_n_clusters, inertia_scores, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Inertia')
plt.title('Inertia for Different Number of Clusters')
plt.xticks(range_n_clusters) # 显示所有x轴刻度
plt.show()
# 打印最小惯性指标和对应的聚类数量
best_inertia_index = np.argmin(inertia_scores)
best_n_clusters = range_n_clusters[best_inertia_index]
best_inertia = inertia_scores[best_inertia_index]
print(f"The best number of clusters based on inertia is: {best_n_clusters}")
print(f"The corresponding inertia is: {best_inertia}")

4.2 轮廓系数(silhouette)
每个样本都有对应的轮廓系数,轮廓系数由两个得分组成:
\(a:\) 样本与同一簇类中的其他样本点的平均距离 ( 即量化凝聚度 );
\(b:\) 样本与距离最近簇类中所有样本点的平均距离 (即量化分离度)。
每个样本的轮廓系数定义为:
其中 \(S=[-1,1]\) 。
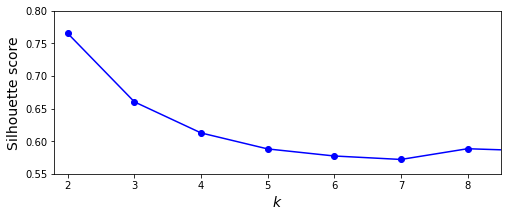
一组数据集的轮廓系数等于该数据集中每一个样本轮廊系数的平均值。轮廓系数既要考虑聚类结果的紧密性,又要考虑聚类结果之间的分离度。如果一个数据点与自己所属的簇内的其他数据点的距离很小,但是与其他簇中的数据点的距离很大,就表示这个数据点所在的簇内紧密度高,簇间分离度大,那么该数据点的轮廓系数就会越大。从上图中我们可以看到当K为2、3时均可取得不错的聚类效果。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
# 提供的数据
data = {
'ID': ['A1', 'A2', 'A3', 'A4', 'A5', 'A6', 'A7', 'A8'],
'X': [3, 3, 4, 4, 1, 1, 2, 2],
'Y': [1, 2, 1, 2, 3, 4, 3, 4]
}
# 创建DataFrame
df = pd.DataFrame(data)
# 提取用于聚类的特征
X = df[['X', 'Y']] # 修正了这里的语法错误
# 初始化KMeans模型列表,并设定k的范围
range_n_clusters = [2, 3, 4, 5] # 根据需要调整范围
silhouette_avg_scores = []
# 对每个k值进行聚类并计算轮廓系数
for n_clusters in range_n_clusters:
# 使用KMeans算法
kmeans = KMeans(n_clusters=n_clusters, random_state=42)
kmeans.fit(X)
# 获取聚类标签
labels = kmeans.labels_
# 计算轮廓系数
silhouette_avg = silhouette_score(X, labels)
silhouette_avg_scores.append(silhouette_avg)
# 绘制轮廓系数随聚类数量变化的图形
plt.figure(figsize=(8, 3))
plt.plot(range_n_clusters, silhouette_avg_scores, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Silhouette Score')
plt.title('Silhouette Score for Different Number of Clusters')
plt.show()
# 打印最佳轮廓系数和对应的聚类数量
best_score_index = np.argmax(silhouette_avg_scores)
best_n_clusters = range_n_clusters[best_score_index]
best_score = silhouette_avg_scores[best_score_index]
print(f"The best number of clusters is: {best_n_clusters}")
print(f"The corresponding silhouette score is: {best_score}")
总结
K-means算法是一种经典的聚类算法,旨在将数据集分成预定数量的簇,通过迭代优化来确定簇的中心点。其基本思想是将数据点划分到最近的簇,通过最小化簇内平方和实现聚类。该算法简单、直观,容易实现,但对初始聚类中心敏感。随着时间的推移,K-means经历了多个发展阶段,包括算法的优化、对大规模数据的处理、提高对异常值的鲁棒性等方面的改进。虽然K-means在许多应用中表现良好,但也存在一些局限性,如对不规则形状的簇处理较弱。在实际应用中,研究者们不断探索K-means与其他技术的结合,以进一步提高聚类效果。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号