随机模拟——蒙特卡洛方法的Python实现
蒙特卡洛方法是一类基于随机抽样的数值计算技术,通过模拟随机事件的概率过程,从而近似计算复杂问题的数学期望或积分。其核心思想是通过大量的随机抽样来逼近问题的解,从而在随机性中获得问题的统计特性。蒙特卡洛方法广泛应用于概率统计、物理学、金融工程、生物学等领域。
在蒙特卡洛模拟中,通过生成符合特定分布的随机样本,计算这些样本的函数值,然后利用样本均值或频率等统计量来估计问题的解。这种方法的优势在于对于高维、复杂的问题,蒙特卡洛方法通常能够提供更为准确的数值结果。随机模拟是蒙特卡洛方法的一种具体应用,它通过对问题中的不确定性因素进行随机抽样,从而模拟问题的多种可能性。在金融风险评估、气象预测、粒子物理实验等领域,随机模拟的蒙特卡洛方法为复杂问题的求解提供了一种强大而灵活的工具。

一、随机模拟的导入
模拟是指把某一现实的或抽象的系统的某种特征或部分状态,用另一系统(称为模拟模型)来代替或近似。为了解决某问题,把它变成一个概率模型的求解问题,然后产生符合模型的大量随机数,对产生的随机数进行分析从而求解问题,这种方法叫做随机模拟方法,又称为蒙特卡洛(MonteCarlo)方法。
例如,一个交通路口需要找到一种最优的控制红绿灯信号的办法,使得通过路口的汽车耽搁的平均时间最短,而行人等候过路的时间不超过某一给定的心理极限值。十字路口的信号共有四个方向,每个方向又分直行、左转、右转。因为汽车和行人的到来是随机的,我们要用随机过程来描述四个方向的汽车到来和路口的行人到来过程。理论建模分析很难解决这个最优化问题。但是,我们可以采集汽车和行人到来的频率,用随机模拟方法模拟汽车和行人到来的过程,并模拟各种控制方案,记录不同方案造成的等待时间,通过统计比较找出最优的控制方案。
随机模拟中的随机性可能来自模型本身的随机变量,比如上面描述的汽车和行人到来,也可能是把非随机的问题转换为概率模型的特征量估计问题从而用随机模拟方法解决。(用随机模拟估计圆周率) 为了计算圆周率\(\pi\)的近似值可以使用随机模拟方法。
如果向正方形\(D = \{(x,y): x \in [-1,1], y \in [-1,1]\}\)内随机等可能投点,落入单位圆\(C = \{(x,y): x^2 + y^2 \leq 1 \}\)的概率为面积之比\(p =\frac{\pi}{4}\)。如果独立重复地投了\(N\)个点,落入\(C\)中的点的个数\(\xi\)的平均值为\(E\xi = pN\),由概率的频率解释,
可以这样给出\(\pi\)的近似值。

import matplotlib.pyplot as plt
import numpy as np
def monte_carlo_pi(num_points):
inside_quadrant = 0
# Scatter points over the square
points = np.random.rand(num_points, 2)
for point in points:
# Check if the point is inside the quadrant
if point[0]**2 + point[1]**2 < 1:
inside_quadrant += 1
# Calculate the ratio and estimate π
ratio = inside_quadrant / num_points
pi_estimate = ratio * 4
return pi_estimate, points
def animate_monte_carlo(num_points_list):
fig, ax = plt.subplots()
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.gca().set_aspect('equal', adjustable='box')
for num_points in num_points_list:
pi_estimate, points = monte_carlo_pi(num_points)
inside_points = points[points[:, 0]**2 + points[:, 1]**2 < 1]
outside_points = points[points[:, 0]**2 + points[:, 1]**2 >= 1]
ax.clear()
ax.scatter(inside_points[:, 0], inside_points[:, 1], color='blue', marker='.')
ax.scatter(outside_points[:, 0], outside_points[:, 1], color='red', marker='.')
ax.set_title(f'Approximated π: {pi_estimate:.6f}')
plt.pause(1)
plt.show()
# Example usage
num_points_list = [100, 500, 1000, 5000, 10000]
animate_monte_carlo(num_points_list)
二、Python的随机数生成函数
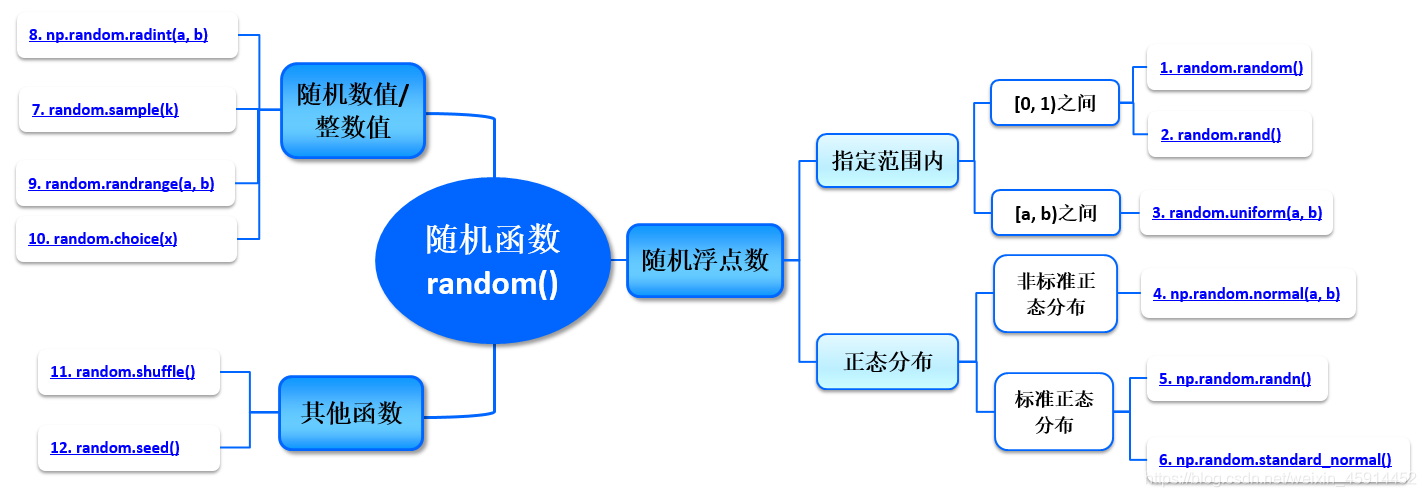
random模块是Python标准库中的一个模块,用于生成各种类型的随机数。它包含了许多函数和方法,可以用于生成伪随机数、从序列中获取随机元素、洗牌等功能。
| 随机函数 | 说明 |
|---|---|
| random.random() | 返回随机生成的一个浮点数,范围在[0,1)之间 |
| random.uniform(a, b) | 返回随机生成的一个浮点数,范围在[a, b)之间 |
| np.random.rand(d0, d1, …, dn) | 返回一个或一组浮点数,范围在[0, 1)之间 |
| np.random.normal(loc=a, scale=b, size=()) | 返回满足条件为均值=a, 标准差=b的正态分布(高斯分布)的概率密度随机数 |
| np.random.randn(d0, d1, … dn) | 返回标准正态分布(均值=0,标准差=1)的概率密度随机数 |
| np.random.standard_normal(size=()) | 返回标准正态分布(均值=0,标准差=1)的概率密度随机数 |
| random.sample(k) | 从总体序列或集合中随机选取k个唯一的元素 |
| np.random.randint(a, b, size=(), dtype=int) | 返回在范围在[a, b)中的随机整数(含有重复值) |
| random.randrange(a, b, step=c) | 在指定范围内,在指定的基数和步长值形成的集合中获取1个随机数值 |
| random.choice(x) | 从指定的序列x中随机获取一个数据 |
| random.shuffle(x) | 将一个列表x中的元素打乱,随机排序(俗称:洗牌) |
| random.seed() | 设定随机种子 |
三、蒙特卡洛算法的基本工作步骤
蒙特卡罗算法一般分为三个步骤,分别为构造随机的概率的过程,从构造随机概率分布中抽样,求解估计量。
构造随机的概率过程:对于本身就具有随机性质的问题,要正确描述和模拟这个概率过程。对于本来不是随机性质的确定性问题,比如计算定积分,就必须事先构造一个人为的概率过程了。它的某些参数正好是所要求问题的解,即要将不具有随机性质的问题转化为随机性质的问题。如本例中求圆周率的问题,是一个确定性的问题,需要事先构造一个概率过程,将其转化为随机性问题,即豆子落在圆内的概率,而π就是所要求的解。
从已知概率分布抽样:由于各种概率模型都可以看作是由各种各样的概率分布构成的,因此产生已知概率分布的随机变量,就成为实现蒙特卡罗方法模拟实验的基本手段。如本例中采用的就是最简单、最基本的(0,1)上的均匀分布,而随机数是我们实现蒙特卡罗模拟的基本工具。
求解估计量:实现模拟实验后,要确定一个随机变量,作为所要求问题的解,即无偏估计。建立估计量,相当于对实验结果进行考察,从而得到问题的解。如求出的近似\(\pi\)就认为是一种无偏估计。
四、随机模拟的应用
4.1 M&M豆问题
M&M豆是有各种颜色的糖果巧克力豆。制造M&M豆的Mars公司会不时变更不同颜色巧克力豆之间的混合比例。1995年,他们推出了蓝色的M&M豆。在此前一袋普通的M&M豆中,颜色的搭配为:30%褐色,20%黄色,20%红色,10%绿色,10%橙色,10%黄褐色。这之后变成了:24%蓝色,20%绿色,16%橙色,14%黄色,13%红色,13%褐色。假设我的一个朋友有两袋M&M豆,他告诉我一袋是1994年,一带是1996年。但他没告诉我具体那个袋子是哪一年的,他从每个袋子里各取了一个M&M豆给我。一个是黄色,一个是绿色的。那么黄色豆来自1994年的袋子的概率是多少?
import time
import random
for i in range(10):
print(time.strftime("%Y-%m-%d %X",time.localtime()))
dou = {1994:{'褐色':30,'黄色':20,'红色':20,'绿色':10,'橙色':10,'黄褐':30},
1996:{'蓝色':24,'绿色':20,'橙色':16,'黄色':14,'红色':13,'褐色':13}}
num = 10000
list_1994 = ['褐色']*30*num+['黄色']*20*num+['红色']*20*num+['绿色']*10*num+['橙色']*10*num+['黄褐']*10*num
list_1996 = ['蓝色']*24*num+['绿色']*20*num+['橙色']*16*num+['黄色']*14*num+['红色']*13*num+['褐色']*13*num
random.shuffle(list_1994)
random.shuffle(list_1996)
count_all = 0
count_key = 0
for key in range(100 * num):
if list_1994[key] == '黄色' and list_1996[key] == '绿色':
count_all += 1
count_key += 1
if list_1994[key] == '绿色' and list_1996[key] == '黄色':
count_all += 1
print(count_key / count_all,20/27)
print(time.strftime("%Y-%m-%d %X",time.localtime()))
# ...
# 0.7407064573459715 0.7407407407407407
# 20/27是理论答案
4.2 定积分计算
利用python计算函数\(y = x^2\)在[0,1]区间的定积分。
import random
m = 1000000
n = 0
for i in range(m):
x = random.random()
y = random.random()
if y >= x ** 2:
n += 1
r = n / m
print("r = {}".format(r))
4.3 三门问题
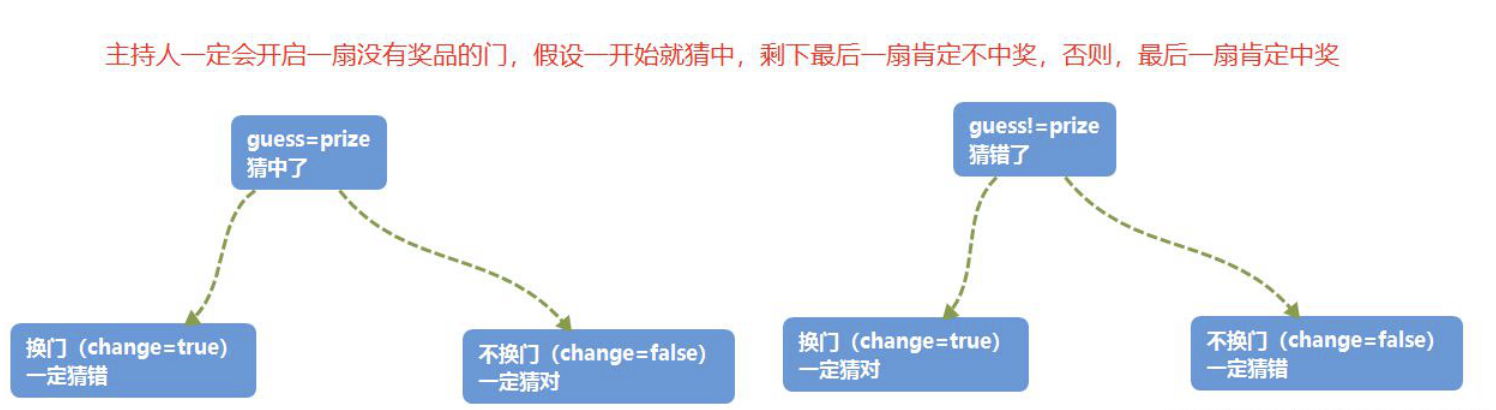
三门问题(Monty Hall problem)亦称为蒙提霍尔问题、蒙特霍问题或蒙提霍尔悖论,大致出自美国的电视游戏节目Let's Make a Deal。问题名字来自该节目的主持人蒙提·霍尔(Monty Hall)。参赛者会看见三扇关闭了的门,其中一扇的后面有一辆汽车,选中后面有车的那扇门可赢得该汽车,另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门,但未去开启它的时候,节目主持人开启剩下两扇门的其中一扇,露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是:换另一扇门会否增加参赛者赢得汽车的机率?如果严格按照上述的条件,即主持人清楚地知道,自己打开的那扇门后是羊,那么答案是会。不换门的话,赢得汽车的几率是1/3。换门的话,赢得汽车的几率是2/3。虽然该问题的答案在逻辑上并不自相矛盾,但十分违反直觉。
def three_doors_question(times: int):
import random
not_change = 0
change = 0
for i in range(0, times):
doors = [1, 2, 3] # 1是汽车
random.shuffle(doors)
first_choice = doors[random.randint(0, 2)]
doors.remove(first_choice)
# 如果汽车在参与者选后剩下的里面,由主持人排除一个错误答案,剩下汽车
if 1 in doors:
doors = [1]
# 如果汽车已经被参与者选了,主持人随机排除剩下一个错误答案
else:
doors.remove(random.choice((2, 3)))
if first_choice == 1:
not_change = not_change + 1
if doors[0] == 1:
change = change + 1
print(
f'模拟次数:{times}, 不更改选择赢得汽车的概率为:{not_change / times}, '
f'更改选择赢得汽车的概率为:{change / times}')
three_doors_question(10000)
three_doors_question(100000)
three_doors_question(500000)
three_doors_question(1000000)
4.4 随机过程的模拟
几何布朗运动的随机微分方程如下,这意味着我们是在等价鞅测度下进行操作:
这里\(W_t\)是一个维纳过程,或者说是布朗运动,而漂移百分比\(\mu\)和波动百分比\(\sigma\)则为常量。
对于上述随机微分方程进行欧拉离散化可以得到离散时间模型:
其中\(S_t\):证券在\(t\)时刻的价格;\(S_{t-\Delta t}\):证券在\(t-\Delta t\)时刻的价格;\(\mu\):证券收益率的期望值;\(\sigma\):证券收益率的波动率;\(\epsilon_t\):服从正态分布(期望为0,方差为1)。
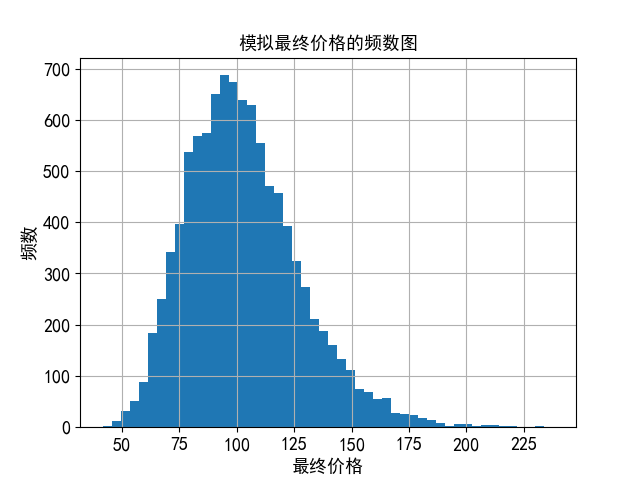
模拟证券初始价格为200(日收益率均值为0.003,波动率为0.25),时间为1年,步长以日为单位,次数为10000次的几何布朗运动价格。
import matplotlib.pyplot as plt
from pylab import mpl
mpl.rcParams['font.sans-serif']=['SimHei']
mpl.rcParams['axes.unicode_minus']=False
import numpy as np
import numpy.random as npr
S0=100 #初始价格
u=0.03 #收益率的均值
sigma=0.24 #收益率的波动率
T=1 #年化时间长度
I=10000 #模拟的次数
M=252 #年化时间分段数目
dt=T/M #模拟的每小步步长
S=np.zeros((M+1,I))
S[0]=S0
for t in range(1,M+1):
S[t]=S[t-1]*np.exp((u-0.5*sigma**2)*dt+sigma*np.sqrt(dt)*npr.standard_normal(I))
#绘制直方图
plt.hist(S[-1],bins=50)
plt.title("模拟最终价格的频数图",fontsize=13)
plt.xlabel(u'最终价格',fontsize=13)
plt.ylabel(u'频数',fontsize=13)
plt.xticks(fontsize=13)
plt.yticks(fontsize=13)
plt.grid(True)
plt.show()
总结
随机模拟,尤其是蒙特卡洛方法,能够通过模拟多种潜在的市场情景,提供更全面、鲁棒的需求预测。以金融衍生品定价为例,蒙特卡洛方法能够在面对复杂金融工具时提供更为精确的估值。在传统的金融市场中,期权定价等问题往往难以用解析方法求解,因为这些金融工具的收益受到多个变量的影响,而这些变量往往难以建立简单的数学模型。蒙特卡洛方法通过模拟这些变量的随机变动,从而估计金融工具的价格。具体而言,假设我们要估计某个股票期权的价格,该期权的价值受到股票价格、波动率、无风险利率等多个因素的影响。我们可以使用蒙特卡洛方法模拟这些因素的未来走势,随机生成多个未来可能的市场情景,计算每种情景下期权的收益,然后取平均值作为期权的估值。这样一来,我们就能够考虑到各种不确定性因素,更全面地评估金融工具的风险。
参考文献
随机分布——连续分布
| 分布大类/形状 | 正式名称 | 参数 | 常见用法 | 备注 |
|---|---|---|---|---|
| 均匀分布 | 连续均匀(uniform)分布 | a(最小值),b(最大值) | - | - |
| 正态分布大类/形状 | 一元高斯分布/正态(Gaussian/Normal)分布 | 数学期望μ(位置参数), 标准差σ(尺度参数) | 根据中心极限定理,可用于描述分布未知的实值随机变量。 | 钟形曲线。是自由度v为无限的学生-t分布 |
| 正态分布大类/形状 | 多元正态分布 | 均值向量μ,方差-协方差矩阵∑ | - | 根据维度而定的钟形形状 |
| 正态分布大类/形状 | 标准一元正态分布 | - | z分数/z分布(错称)/t分数(日语:偏差值) | 期望为0,标准差为1 |
| 正态分布大类/抽样分布 | 学生t-(Student's t-)分布 | v(df,自由度) | 仅适用于统计方法中。 | 半重尾分布。广义双曲分布的特殊情况。(不是tau分布) |
| 正态分布大类/形状 | 对数正态(Log/Log-normal)分布 | 数学期望μ(位置参数), 标准差σ(尺度参数) | 如某个分布是正态分布,则它的对数服从对数正态分布。 | |
| 统计检验方法分布/抽样分布 | (中心)F-分布 | d1, d2(df,自由度) | 仅适用于统计方法中。 | - |
| 统计检验方法/机器学习方法分布 | 逻辑(Logistic)分布 | μ(位置参数), s(尺度参数) | 仅适用于统计方法/机器学习中。 | 类似正态分布,但属于肥尾/长尾分布。 |
| 统计检验方法分布/抽样分布/伽马分布大类 | 卡方分布 | k(df,自由度) | 仅适用于统计方法中。 | 隶属于伽马分布。k个独立的标准正态分布变量的平方和服从自由度为k的卡方分布。 |
| 伽马分布大类/形状 | 伽马(γ)分布 | k(形状参数),θ(逆尺度参数)或α,β(基本一致,k=α,β与θ可以互转) | 大量真实案例的分布,跨多个学科。例如收入(劳工市场的薪酬)、生产力、生命长度等。 | 许多似然分布(例如泊松分布、指数分布、已知均值的正态分布、帕累托分布和已知σ的伽玛/逆伽玛)的共轭先验分布。 |
| 伽马分布大类/形状 | 指数(Exponential )分布/负指数分布 | α = 1 | 可用于独立随机事件发生的时间间隔。 | 适用于泊松事件流的等待时间。 |
| 其他常用 | 柯西(-洛伦兹)分布 | x0(位置参数),γ(尺度参数) | - | 肥尾/长尾分布。概率密度函数无限延伸,因此没有期望与标准差。易与正态分布弄混。其称呼洛伦兹分布与洛伦兹曲线没有半毛钱关系。 |
| 其他常用 | 标准柯西分布 | - | - | 位置参数为0,尺度参数为1。自由度v为1的学生t-分布 |
| 其他常用 | 贝塔(β/B)分布 | α,β(均为形状参数) | 可用于概率建模。 | 值域在0与1之间,因此,适合作为伯努利分布和二项式分布的共轭先验分布。 |
| 其他常用 | 狄利克雷分布/多元Beta分布 | K(类别数),α(浓度参数) | - | 贝塔分布在高维/多元时的情况。适合作为多元正态分布、分类分布和多项分布的的共轭先验分布。 |
| 其他常用 | 拉普拉斯分布/双指数分布 | μ(位置参数),b(尺度参数) | - | - |
| 其他常用 | 帕累托分布/布拉德福分布 | xm,k | 大量真实案例的分布,跨多个学科。例如,财富在个人之间的分配就属于帕累托分布。 | 常用于经济学中。 |
| 其他常用 | tau分布 | - | 可用于残差统计 | 贝塔分布的特例。用于误差独立且正态分布情况下,学生化残差的概率分布。 |
随机分布——离散分布
| 分布大类/形状 | 正式名称 | 参数 | 常见用法 | 备注 |
|---|---|---|---|---|
| 泊松分布 | 泊松(Poisson)分布 | λ(速率) | 独立事件在一定时间内的发生次数(计数) | 可应用于具有大量可能事件且每个事件都很少发生的系统。 |
| 二项式分布大类 | 伯努利(Bernoulli)分布 | p(概率) | 单个实验的可能结果集(二分) | n=1的二项式分布 |
| 二项式分布大类 | 二项(Binominal)分布 | p(概率)、n(实验次数) | n个独立实验序列中的成功次数(二分) | - |
| 二项式分布大类 | 负二项(Negative Binominal)分布 | r(成功次数)、p(概率) | 到r次成功时即终止的独立试验中,失败次数k | - |
| 二项式分布大类 | 分类(Categorical)分布 | pk(事件概率),k(类别数) | 单个实验的可能结果集(多项) | 伯努利分布的推广,与多项分布常弄混 |
| 二项式分布大类 | 多项(Multinominal)分布/多项式分布 | pk(事件概率)、k(互斥事件的数量)n(实验次数) | n个独立实验序列中的成功次数(多项) | 二项分布的推广 |
| 二项式分布大类 | 几何(Geometric)分布 | p(概率) | 第一次成功/失败所进行的试验次数(计数) | 负二项分布的特殊形式(r=1) |
| 其他常用 | 超几何(Hypergeometirc)分布 | N(总体数目),n(样本数目),M(特征对象) | 从有限N个物件(其中包含M个指定种类的物件)中抽出n个物件,不放回情况下,成功抽出该指定种类的物件的次数 | 与几何分布实际没有关系 |
| 释疑 | 对数(Logarithmic/log-series)分布/对数级数分布 | p | - | 常用于保险业、生物学与微生物学中。不要与对数正态分布(Log/Lognormal)弄混。 |



 浙公网安备 33010602011771号
浙公网安备 33010602011771号