系统评价——数据指标的规范化处理（一）

在多指标评价体系中，由于各评价指标的性质不同，通常具有不同的量纲和数量级。当各指标间的水平相差很大时，如果直接用原始指标值进行分析，就会突出数值较高的指标在综合分析中的作用，相对削弱数值水平较低指标的作用。因此，为了保证结果的可靠性，需要对原始指标数据进行规范化处理。目前数据规范化方法有多种，归结起来可以分为直线型方法(如极值法、标准差法)、折线型方法(如三折线法)、曲线型方法(如半正态性分布)。不同的规范化方法，对系统的评价结果会产生不同的影响，然而不幸的是，在数据规范化方法的选择上，还没有通用的法则可以遵循。
！！！数据规范化前要注意数据的属性（极大型、极小型、中间型）以及数据发展变化规律（正指标、负指标）。

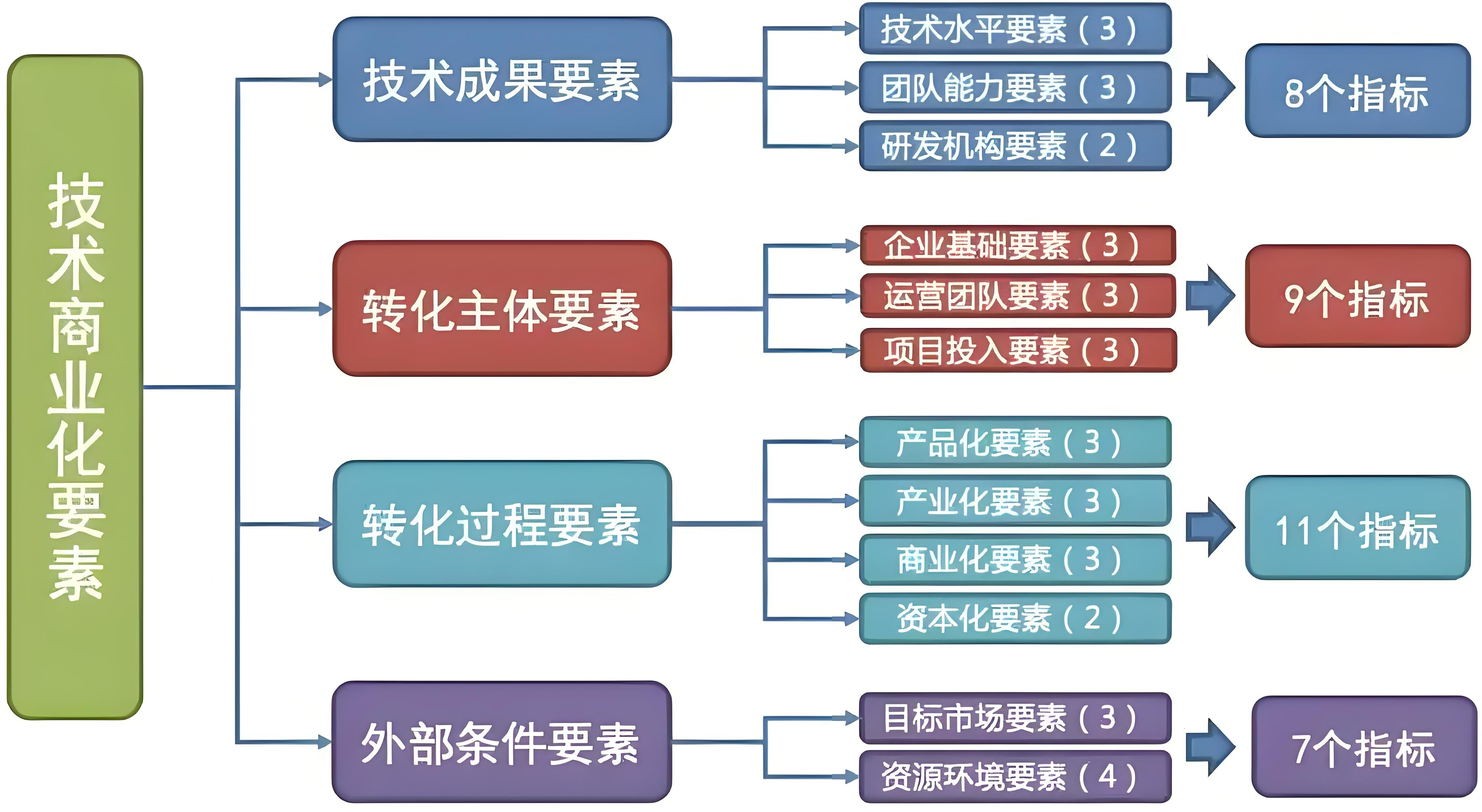
一、数据指标为什么要规范化？

数据指标的规划化实质是一种线性变换，线性变换有很多良好的性质，这些性质决定了对数据改变后不会造成“失效”，反而能提高数据的表现，这些性质是归一化/标准化的前提。比如有一个很重要的性质：线性变换不会改变原始数据的数值排序。

• 数据的量纲不同，数量级差别很大
  经过规范化处理后，原始数据转化为无量纲化指标测评值，各指标值处于同一数量级别，可进行综合测评分析。如果直接用原始指标值进行分析，就会突出数值较高的指标在综合分析中的作用，相对削弱数值水平较低指标的作用。
• 避免数值问题：太大的数会引发数值问题。
• 平衡各特征的贡献
  一些分类器需要计算样本之间的距离（如欧氏距离），例如KNN。如果一个特征值域范围非常大，那么距离计算就主要取决于这个特征，从而与实际情况相悖（比如这时实际情况是值域范围小的特征更重要）。
• 一些模型求解的需要：加快了梯度下降求最优解的速度
  在使用梯度下降的方法求解最优化问题时，规范化后可以加快梯度下降的求解速度，即提升模型的收敛速度。

二、指标预处理——转化为正指标

选取合理的评价指标是综合评价问题的第一步，要考虑四个准则——代表性、确定性、独立性、区别能力。
代表性：各层次指标能最好地表达所代表的层次；
确定性：指标值要确定、可量化，高低在评价中有确切的含义；
独立性 ：选定的指标要互相独立，不能相互替代；
区别能力/灵敏性：指标有一定的波动范围。

2.1 指标的属性分类

在我们选取的众多评价指标中，有些指标数值越大越好（“极大型”指标），有些指标越小越好（“极小型”指标），有些指标是在一定范围内（“区间型”指标）。

极大型指标：总是期望指标的取值越大越好；
极小型指标：总是期望指标的取值越小越好；
中间型指标：总是期望指标的取值既不要太大，也不要太小为好，即取适当的中间值为最好;
区间型指标：总是期望指标的取值最好是落在某一个确定的区间内为最好。

指标名称	指标特点	例子
极大型（效益型）指标	越大（多）越好	成绩、GDP增速、企业利润
极小型（成本型）指标	越小（少）越好	费用、坏品率、污染程度
中间型指标	越接近某个值越好	水质量评估时的PH值
区间型指标	落在某个区间最好	体温、水中植物性营养物量

例如我们在期末进行综合测评时，评价指标中有学习成绩、缺课率等，学习成绩这项指标是取值越大越好，是极大型指标，学习成绩越高，综合测评得分相应越高；缺课率这项指标是越小越好，是极小型指标，缺课率越高，综合测评得分越低。因此，我们需要对指标进行一致化处理，将所有的指标转化为极大型指标或者极小型指标。

2.2 指标的转化公式

极大型指标（效益类指标），也就是正指标，不做处理
极小型指标（成本类指标）：

\[\overline{x}_i=max\{x_i\} -x_i \quad 或 \quad \frac{1}{x_i} \]

中间型指标：
中间型指标的特点：指标的值既不要太大也不要太小，取某个特定的值最好(例如：评估水质量用到的PH值)
\(\{ x_i \}\) 是 一组中间型指标序列，且最佳的数值为\(x_{best}\) , 那么正向化的公式如下：

\[\overline{x}_i=1- \frac{\left| x_i-x_{best} \right|}{max∣x_i​−x_{best} ​∣} \]

区间型指标：

\(\{x_i​\}\)是一组区间型指标序列，且最佳的区间为\([a,b]\)，那么正向化的公式如下：

\[M=max \{ a-min\{ x_i \}，max\{ x_i \} -b \} \]

\[\overline{x}_i=\begin{cases} 1-\frac{a-x_i}{M},x_i<a\\ 1 ,a\leqslant x_i\leqslant b\\ 1-\frac{x_i-b}{M},x_i>b\\ \end{cases} \]

三、数据规范化方法

数据的规范化(normalization)是将数据按比例缩放，使之落入一个小的特定区间。在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。其中最典型的就是数据的归一化处理，即将数据统一映射到\([0,1]\)区间上，常见的数据归一化的方法有：min-max标准化（Min-max normalization），z-score标准化（zero-mena normalization，此方法最为常用），模糊量化法。

3.1 min-max规范化(Min-maxnormalization)

也叫离差标准化，是对原始数据的线性变换，使结果落到[0,1]区间，转换函数如下:

对序列\(x_1,x_2,...,x_n\)进行变换

\[y_i=\frac{x_i-\underset{1\le i \le n}{min}\{x_i\}}{\underset{1\le i \le n}{max}\{x_i\}-\underset{1\le i \le n}{min}\{x_i\}} \]

则新序列\(y_1,y_2,...,y_n \in [0,1]\)且无量纲，不同类型的数据加权时都要进行规范化处理。

离差标准化

• 其中max为样本数据的最大值，min为样本数据的最小值。
• 这种方法有一个缺陷就是当有新数据加入时，可能导致max和min的变化，需要重新定义。

3.2 z-score规范化(zero-meannormalization)

并不是所有数据规范化的结果都映射到\([0,1]\)区间上，其中最常见的标准化方法就是Z标准化，也叫标准差标准化。通过规范化，令数据的平均值为 0，标准化为1的标准化方法，在经济社会、传播学研究中使用普遍，公式如下：

\[\hat x_i = \frac{x_i - \mu}{\sigma}, \hspace{1em}x \in R \]

其中\(\mu\)为样本均值， \(\sigma\)为样本标准差。

优点：

• 保留数据真实距离，维持标准化前数据分布，缩放均为等比例缩放。
• 标准化后数据的平均值为0，标准化为1。
• 对极值不敏感。
  缺点：
• 标准化后数据不在固定范围内，如用作指标体系计算还需要进一步标准化。
• 样本标准化后值不稳定，受样本平均值和标准差影响；当添加新样本时，旧样本的标准化值一定发生变化。

3.3 Sigmoid 函数规范化

如果数据呈现中间集中的分布，同时需要将区分中心部分的差距，可以使用 Sigmod 函数进行标准化，公式如下：

\[\hat x_i = \frac{1}{1+e^{-(x_i - a) \times b}}, \hspace{1em} x \in R,\hat x_i∈(0,1) \]

其中系数\(a\)为需要区分部分中心的值，系数\(b\)为需要区分的程度。

优点：

• 扭曲了原数据，扩大（加强）了某个中心附近的样本值之间的差距，缩小（减弱）了距离该中心较远的样本值之间的差距。
• 对极小值和极大值均完全不敏感。
• 样本标准化后的值稳定，不受样本最大值和最小值的影响。
  缺点：
• 对距离中心较远的样本值之间的差距 非常 不敏感。

3.4 归一化处理

\[x_{new}=\frac{x}{x_{1}+x_{2}+...+x_{n}} \]

对正数进行变换，使结果落到\([0,1]\)区间，其将数值的绝对值变成相对值关系

3.5 模数单位化

\[x_{new}=\frac{x}{||x||} \]

将每个样本的特征向量除以其长度，即对样本特征向量的长度进行归一化，长度的度量常使用的是L2 norm（欧氏距离），有时也会采用L1 norm。

四、几种规范化方法的比较

方法	公式	优点	缺点	适用场景
Min-Max 规范化	$$y_i = \frac{x_i - \min{x}}{\max{x} - \min{x}}$$	- 简单易懂 - 保持原始数据关系	- 对异常值敏感 - 新数据需重新计算最大值和最小值	数据范围固定且稳定的情况
Z-Score 规范化	$$\hat{x}_i = \frac{x_i - \mu}{\sigma}$$	- 对异常值不敏感 - 保持数据分布（均值为0，标准差为1）	- 数据范围不固定 - 新样本会影响所有数据的标准化值	需要数据中心化和标准化的场景
Sigmoid 函数规范化	$$\hat{x}_i = \frac{1}{1 + e^{-(x_i - a) \times b}}$$	- 强化中心区间差距 - 对极端值不敏感	- 对远离中心的数据差距不敏感 - 参数选择困难	数据中有明确中心且需强化的情况
归一化处理	$$x_{\text{new}} = \frac{x}{\sum_{i=1}^n x_i}$$	- 将数据转化为相对值 - 简单直观	- 对数据分布有要求	数据总和具有实际意义的场景
模数单位化	$$x_{new} = \frac{x}{||x||}$$	- 保持数据方向性 - 对数据范围不敏感	对范数计算依赖	高维空间数据处理，如文本分析

总的来说，规范化/归一化/标准化的目的是为了获得某种“无关性”——偏置无关、尺度无关、长度无关……当规范化/归一化/标准化方法背后的物理意义和几何含义与当前问题的需要相契合时，其对解决该问题就有正向作用，反之，就会起反作用。所以，“何时选择何种方法”取决于待解决的问题，即problem-dependent。

五、数据指标规范化的基本步骤

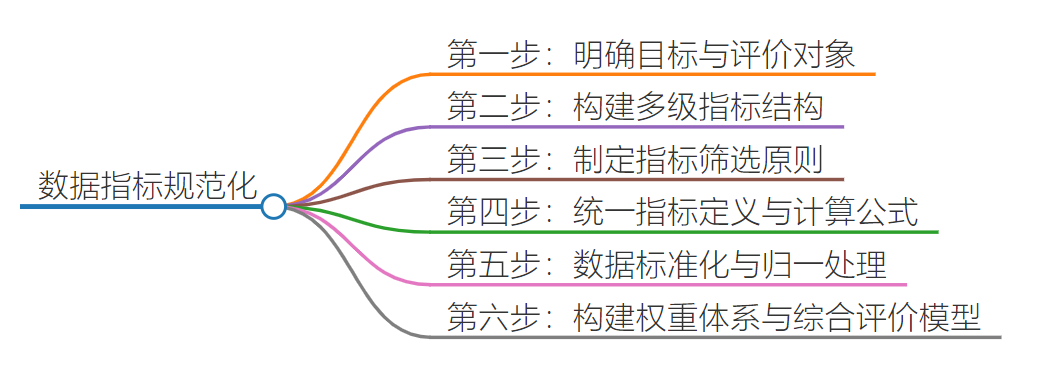
指标体系的规范化建设是一项系统工程，通常需遵循以下六个主要步骤：

第一步：明确目标与评价对象

规范化的第一步是界定评价目标与研究对象。不同目标（如绩效评估、风险控制、发展潜力预测）决定指标选择的方向；不同对象（如企业、区域、行业、产品）决定评价维度的内容。因此，需通过调研、访谈或专家咨询，明确指标体系服务的具体任务与业务场景。

第二步：构建多级指标结构

常采用“层次化结构”，即从总体目标出发，逐层细化指标，如常见的“目标层—准则层—指标层”。例如，绿色发展指标体系可分为环境、资源、经济、社会等一级指标，下面再细分为空气质量、能耗、水资源利用率等二级和三级指标。规范化设计应确保结构完整、分类清晰、无交叉重复。

第三步：制定指标筛选原则

指标的选取应遵循科学性、可量化性、相关性、可操作性等原则。规范化过程中要评估每个指标的代表性、独立性和可获得性，剔除主观性强或数据难以采集的冗余项。常用方法包括德尔菲法、层次分析法（AHP）、熵权法等，确保体系简洁而不失全貌。

第四步：统一指标定义与计算公式

这是规范化的核心环节。每一个指标都需明确定义、单位、计算方法、统计周期与数据来源。例如，“单位GDP能耗”应统一为“吨标准煤/万元GDP”，以固定价格计算；“员工流失率”应规定统计口径（如以年初在岗人数为基数）。这一阶段要求形成“指标说明书”，保障指标的准确解释与一致使用。

第五步：数据标准化与归一处理

由于不同指标具有不同量纲和方向（正向或反向），在规范化体系中应规定数据预处理方式。例如采用极差标准化、Z分数标准化或Min-Max归一化方法，使得不同维度指标具有可比性。同时需明确正向指标与反向指标的处理逻辑（如污染物排放为反向指标，值越小越好）。

第六步：构建权重体系与综合评价模型

规范化指标体系通常还包括权重设计与综合评分机制。需结合专家判断（主观赋权）与数据驱动方法（如熵权法、主成分分析）合理确定各指标权重，以反映其在总体目标中的相对重要性。随后采用线性加权法、TOPSIS、灰色关联度法等方法计算综合得分，为后续评价排序或分类提供依据。

指标体系的规范化不仅是一种技术规范，更体现了对数据质量、分析逻辑和系统治理能力的追求。通过科学设计和严谨实施，规范化指标体系能够实现“数据驱动—科学评价—精准决策”的闭环，广泛应用于政府管理、企业经营、社会评价、项目审计等各类领域。在数字经济和智能决策日益发展的背景下，其规范化建设的重要性愈发凸显，已成为现代组织实现高质量发展的基础能力之一。

总结

评价是现代社会各领域的一项经常性的工作，是科学做出管理决策的重要依据。随着人们研究领域的不断扩大，所面临的评价对象日趋复杂，如果仅依据单一指标对事物进行评价往往不尽合理，必须全面地从整体的角度考虑问题，多指标综合评价方法应运而生。评价往往是由多个评价指标构成的，而这些评价指标往往具有不同的属性、数量级和单位，这导致我们无法对不同的指标进行比较、加权、求和等种种后续操作。假设各个指标之间的水平相差很大，此时直接使用原始指标进行分析时，数值较大的指标，在评价模型中的绝对作用就会显得较为突出和重要，而数值较小的指标，其作用则可能就会显得微不足道。因此，为了消除不同评价指标之间存在的差异，统一比较的标准，就需要对数据进行标准化处理，消除不同指标之间因属性不同而带来的影响，从而使结果更具有可比性。

参考文献

几种常用数据标准化方法
指标体系中的标准化方法
数据处理——常见标准化方法总结
数据规范化(normalization)
数学建模：Topsis法（优劣解距离法）

数据离散化是指将连续变量的取值区间划分为若干个不重叠的小区间，并将每个区间赋予一个唯一标识，转化为离散变量，常用于数据挖掘与机器学习预处理环节。离散化的核心是从细致的数值表示中提取出具有概括性的信息。常见方法包括：
（1）等宽法：将数值范围均匀划分为若干等宽区间，简单易操作，但对离群值敏感，易造成区间样本不均衡；
（2）等频法：将相同数量的样本分入各个区间，有助于数据均衡，但可能将相同值分入不同区间，造成信息割裂；
（3）基于聚类的分箱：利用如K-Means聚类将数据聚成若干簇，对数据分布自适应，适合复杂场景；
（4）分箱处理（Binning）：是一种综合的离散化技术，可结合统计规则、模型结果或业务经验进行灵活划分，在评分卡模型中广泛应用。
合理的离散化和分箱有助于提升模型性能、降低过拟合风险，并增强模型的可解释性，是特征工程的重要环节。