图与网络分析(一)—igraph包概要
图与网络理论是运筹学的重要分支之一,在经济管理领域具有广泛的应用。运筹学旨在利用数学模型和优化方法,为复杂决策问题提供科学依据,而图与网络模型则在资源配置、物流管理、金融网络、供应链优化等方面发挥关键作用。通过将现实经济管理问题抽象为图或网络结构,可以利用图论中的最短路径、最大流、最小生成树、匹配问题等经典算法进行求解。例如,在交通运输领域,最短路径问题能够优化物流配送路线,提高运输效率;在金融市场中,网络模型可用于分析系统性风险,优化资产配置。特别是大数据与人工智能技术的发展,图神经网络(GNN)等新兴方法使得图与网络模型在预测、分类及优化问题中的应用更加广泛。这里介绍如何在 R 语言中进行图的绘制与操作,以及图的矩阵表示方法。

一、R的igraph包
一个网络\(G\),也可以称为图(graph)或网络图,是一种包含了节点\(V\)(即网络参与者,也称顶点)与边\(E\)(即节点之间的连接关系)的数学结构,记作\(G=\{V,E\}\)。可以使用一个矩阵来存放节点之间的连接关系,这个矩阵称为邻接矩阵。如果网络中两个节点之间的边是有方向的,即从节点\(u\)出发指向节点\(v\),这就是一个有向网络(有向图),否则称为无向网络(无向图)。网络的边也可以赋予权重,称为加权网络。
1.1 建立图形对象
igraph包是一个用来解决图与网络问题以及对其进行可视化的包。igraph是一个“历史悠久”的开源项目,提供了一组简单易用且功能强大的网络分析工具,igraph有多种语言接口,包括了R\Python\C++等等。尽管(无论在R还是Python中)已经有了更多的网络分析和可视化工具,igraph依然是最好的出发点。
make_graph()是igraph包中用于创建图的核心函数,其一般形式如下:
make_graph(edges, ..., n = max(edges), isolates = NULL, directed = TRUE, dir = directed, simplify = TRUE)
make_graph() 参数说明表
| 参数 | 类型 | 说明 |
|---|---|---|
| edges | 向量 | 定义图的边,可以是数字或字符,格式如c(1,2, 2,3) |
| n | 整数 | 指定最大节点数,仅在edges 为数字时生效,通常可省略 |
| isolates | 向量 | 指定孤立点,仅在edges 为字符时生效,如isolates = c(d, e) |
| directed | 逻辑值 | 是否创建有向图,TRUE 表示有向图,FALSE 表示无向图 |
| dir | 逻辑值 | 与directed 相同,不能与directed 同时使用 |
| simplify | 逻辑值 | 仅在edges 使用 literals 时有用,控制是否去除多重边和自环 |
library(igraph)
# 创建一个有向图
g1 <- make_graph(c(1,2, 2,3, 3,4), directed = TRUE)
plot(g1)
# 创建一个无向图,并包含孤立点
g2 <- make_graph(c("A", "B", "B", "C"), isolates = c("D", "E"), directed = FALSE)
plot(g2)
这个函数能够构建各种类型的网络结构。
1.2 应用函数
igraph提供了丰富的图计算功能,在经济管理、社交网络分析、供应链优化等多个领域具有重要应用。例如,可以计算最短路径、检测网络中的社区结构,并可视化复杂的网络关系。
最短路径计算(Shortest Path)
# 计算节点 1 到 4 的最短路径
shortest_path <- shortest_paths(g1, from = 1, to = 4)
print(shortest_path$vpath)
图的可视化(Graph Visualization)
# 使用不同的布局进行可视化
plot(g1, layout = layout_with_fr, vertex.color = "lightblue", edge.arrow.size = 0.5)
社区检测(Community Detection)
# Louvain 社区检测
community <- cluster_louvain(g1)
print(membership(community))
# 可视化社区
plot(community, g1)
igraph 核心操作与功能表
| 功能类别 | 相关函数 | 说明 |
|---|---|---|
| 最短路径计算 | shortest_paths() |
计算两个节点之间的最短路径 |
distances() |
计算所有节点对之间的最短路径距离 | |
get.shortest.paths() |
获取具体的最短路径路径 | |
| 图的可视化 | plot() |
绘制图结构,可调整布局和样式 |
tkplot() |
交互式可视化 | |
ggraph() |
基于 ggplot2 的高级可视化 |
|
layout_with_fr() |
Fruchterman-Reingold 布局,适合社交网络 | |
| 社区检测 | cluster_louvain() |
Louvain 方法检测社区 |
cluster_fast_greedy() |
基于模块度优化的快速贪心方法 | |
cluster_walktrap() |
随机游走方法检测社区 | |
| 其他图计算 | degree() |
计算节点的度(连接数) |
as_adj() |
获取邻接矩阵 | |
as_edgelist() |
获取边列表 |
| 应用领域 | 具体应用示例 |
|---|---|
| 供应链优化 | 通过图分析物流网络,优化运输路径,降低成本 |
| 社交网络分析 | 识别关键影响者,分析信息传播模式 |
| 经济管理 | 研究企业关系网络,分析市场结构 |
| 风险评估 | 通过网络模型评估金融风险,预测市场波动 |
二、图的数据结构
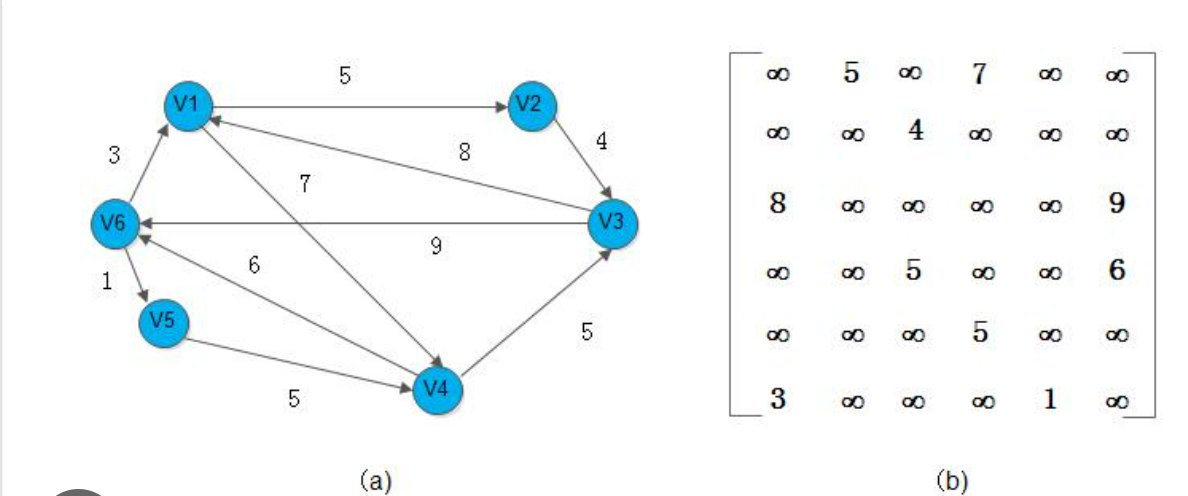
图是一组顶点:通常用\(V(Vertex)\)表示顶点集合;一组边:通常用\(E (Edge)\)表示边的集合,边是顶点对:如\((v, k) ∈E\) ,其中\(v, k ∈ V\);有向图的边表示从\(v\)指向\(k\)的边(单行线),无向图的边是无向边\((v, k)\)(双向线);边的权:通常用\(W(Weight)\)表示权的集合,这三个集合构成的三元有序组就表示一个赋权图。简单图一般不考虑多重边和自回路,如下图所示。
# 加载 igraph 包
library(igraph)
# 创建边信息矩阵,包含起点、终点和权重
m <- matrix(c(1,2,6, 1,3,5, 1,4,4, 1,6,4,
3,6,4, 3,7,3, 4,7,3, 5,8,5,
6,8,4, 7,8,6), ncol = 3, byrow = TRUE)
# 创建无向图
g <- make_graph(t(m[,1:2]), directed = FALSE)
# 创建有向图
h <- make_graph(t(m[,1:2]), directed = TRUE)
# 为图加载权重属性
graph_attr(g, "weight") <- m[,3]
graph_attr(h, "weight") <- m[,3]
# 另一种方式为边赋权重
E(g)$weight <- m[,3]
E(h)$weight <- m[,3]
# 获取图的权重信息
graph_attr(g, "weight") # 获取无向图 g 的权重
graph_attr(h, "weight") # 获取有向图 h 的权重
# 绘制无向图,边标签为权重
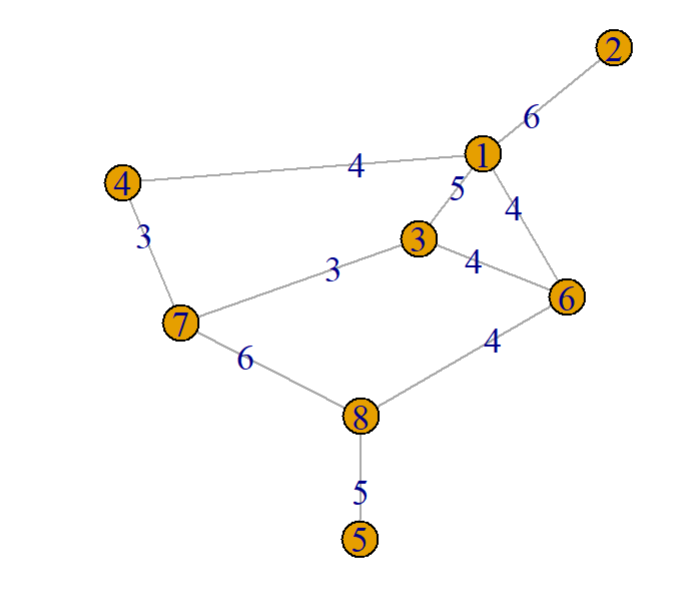
plot(g, edge.label = E(g)$weight, main = "无向图")
# 绘制有向图,边标签为权重
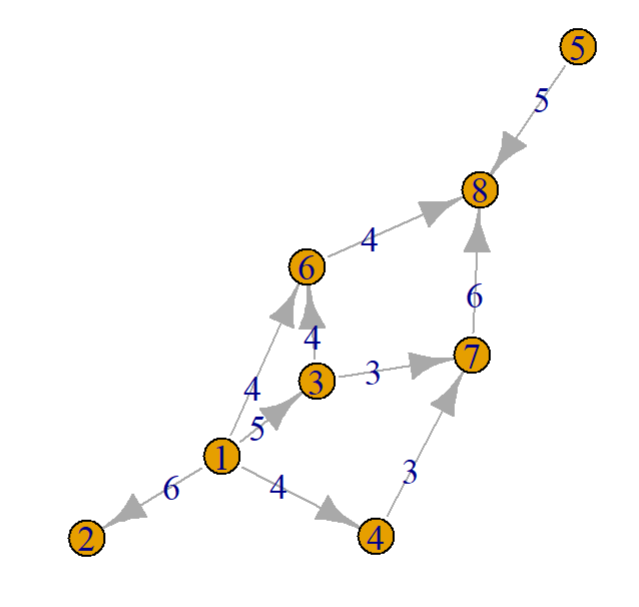
plot(h, edge.label = E(h)$weight, main = "有向图")
| 无向图1 | 有向图2 |
|---|---|
 |
 |
连通图:如果从\(v\)到\(k\)存在一条(无向)路径,则称\(v\)和\(k\)是连通的。连通图(Connected Graph):如果对于图的任一两个顶点\(v、k∈V\),\(v\)和\(k\)都是连通的,则称该图为连通图。连通是图最重要的性质,表面我们所研究的对象图是一个有机整体。
2.1 图的邻接矩阵
邻接矩阵(Adjacency Matrix)是表示顶点之间相邻关系的矩阵。设任意图\(G=(V,E)\),其中顶点集\(V=\{v_1,v_2,...,v_n\}\),边集\(E=\{e_1,e_2,...,e_t\}\) ,称矩阵 $$A(G)=[a_{ij}]_{n×n}$$ 为图G的邻接矩阵,其中
G的邻接矩阵是一个的\(n\)阶方阵:
①对无向图而言,邻接矩阵一定是对称的,而且主对角线一定为零(在此仅讨论无向简单图),副对角线不一定为0,有向图则不一定如此。
②无向图的邻接矩阵一定是对称的,而有向图的邻接矩阵不一定对称。
无向网络的邻接矩阵(对称阵)
若节点\(i\)和节点\(j\)之间存在连接,则令矩阵中第\(i\)行第\(j\)列上的元素\(a_{ij}=1\);若节点\(i\)和节点\(j\)之间不存在连接,则令矩阵元素\(a_{ij}=0\)。

有向矩阵的邻接矩阵(非对称阵)
若节点\(i\)和节点\(j\)之间存在有向连接,则令矩阵元素\(a_{ij}=1\);若节点\(i\)和节点\(j\)之间不存在有向连接,则令矩阵元素\(a_{ij}=0\)。

图1的邻接矩阵为
get.adjacency(g)
[1,] . 1 1 1 . . . .
[2,] 1 . . . . 1 . .
[3,] 1 . . . . 1 1 .
[4,] 1 . . . . . 1 .
[5,] . . . . . . . 1
[6,] . 1 1 . . . . 1
[7,] . . 1 1 . . . 1
[8,] . . . . 1 1 1 .
图2的邻接矩阵为(!!!有向边默认以行为起点)
get.adjacency(h)
[1,] . 1 1 1 . . . .
[2,] . . . . . 1 . .
[3,] . . . . . 1 1 .
[4,] . . . . . . 1 .
[5,] . . . . . . . 1
[6,] . . . . . . . 1
[7,] . . . . . . . 1
[8,] . . . . . . . .
2.2 赋权图的加权邻接矩阵(Labeled Adjacency Matrix)
加权邻接矩阵是把图的顶点视为一个矩阵,其中的数字代表着顶点之间的权重。对于赋权图\(G=(V,E,W)\),其边\((v_i,v_j)\)的权重为\(w_{ij}\),构造矩阵\(A(G)=[a_{ij}]_{n×n}\),其中
若节点\(i\) 和节点\(j\)之间存在连接,则令矩阵中第\(i\)行第\(j\)列上的元素\(a_{ij}=w_{ij}\);若节点\(i\)和节点\(j\)之间不存在连接,则令矩阵元素\(a_{ij}=0\)。可见,网络的邻接矩阵是加权网络的特例,是权重值只有1和0两个取值的加权邻接矩阵。

| A | B | C | D | E | |
|---|---|---|---|---|---|
| A | 0 | 2 | 0 | 0 | 2 |
| B | 0 | 0 | 4 | 4 | 0 |
| C | 0 | 0 | 0 | 6 | 0 |
| D | 0 | 0 | 0 | 0 | 8 |
| E | 0 | 10 | 0 | 0 | 0 |
图1的加权邻接矩阵
get.adjacency(g,attr = "weight",sparse = T)
[1,] . 6 5 4 . . . .
[2,] 6 . . . . 4 . .
[3,] 5 . . . . 4 3 .
[4,] 4 . . . . . 3 .
[5,] . . . . . . . 5
[6,] . 4 4 . . . . 4
[7,] . . 3 3 . . . 6
[8,] . . . . 5 4 6 .
加权邻接矩阵是一种用来表示网络节点之间的连接结构,以及不同用户的相似度的矩阵,它的作用不容小觑。在图论领域,加权邻接矩阵可以用来描述图的拓朴结构,也可以用来解决最短路径问题,在人工智能领域、金融工程领域甚至许多应用领域中还有十分广泛的应用。
2.3 图的边缘列表(Edge List)
边缘列表,也称边列表,图的储存结构之一。边缘列表(EL),是具有连接顶点及其权重的边的集合,因此其空间开销为E(边的数量)。

| 边索引 | from | to |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 2 |
| 2 | 1 | 2 |
| 3 | 1 | 3 |
| 4 | 2 | 4 |
| 5 | 3 | 4 |
| 6 | 4 | 5 |
| 7 | 5 | 6 |
在上图中,共有8条边,因此列表的长度为8,在数据表示中,因为是无权重图,所以权重值并未体现出来,如顶点0,与顶点1和顶点2相连,可以看到EL[0]=(0,1) ,EL[1]=(0, 2)。为了提高查询的效率,我们已经对上方的数组使用排序函数先按照起点排序,再按照终点排序,这样完成后,相同的起点的边就是挨在一起的,相同起点的终点也是有顺序的,查询起来相对会快一些。
图1的边列表
get.data.frame(g)
from to
1 1 2
2 1 3
3 1 4
4 2 6
5 3 6
6 3 7
7 4 7
8 5 8
9 6 8
10 7 8

参考文献



 浙公网安备 33010602011771号
浙公网安备 33010602011771号