Egret-2d实现Gallery(轮播图) 理论

Egret-2d实现Gallery(轮播图) 理论

1、用3D模拟，具体参考cocos2dx 实现gallery(一)、cocos2dx 实现gallery(二)、cocos2dx 实现gallery(三)、cocos2dx 实现gallery(四)、cocos2dx 实现gallery(五)

1.1、先看我们要实现的效果，应该是在3D空间内，有一个圆，圆周放置了很多矩形，我们从某一个点去看这些矩形

正面看上去应该是这样的

从顶面向下俯视应该是这样的，红色的表示是我们眼睛的方向

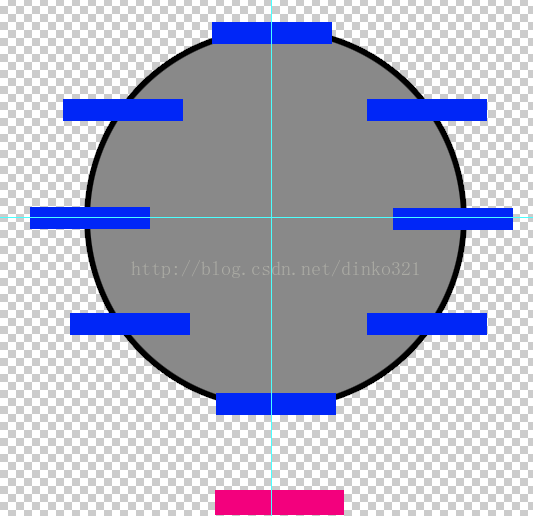
从侧面看应该是这样的

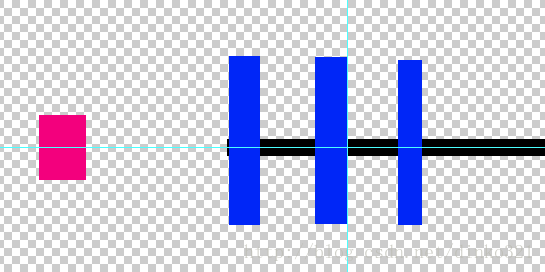
我们先把前面的模型简化，我们最后要看到的是这样:

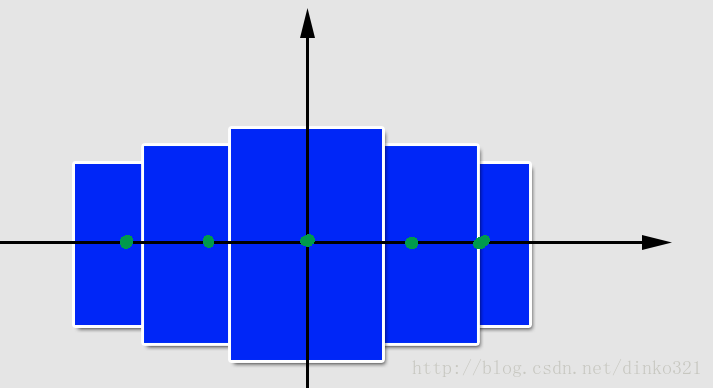
1.2、这个图上，构成这个效果的主要因素有3个：

  1)、x方向的位置，就是图上绿点标记的地方，锚点0.5
  2)、大小，有了大小的差别，就有了远近的差别
  3)、zorder，这个是决定遮挡关系，然后我们就会产生一种立体的错觉

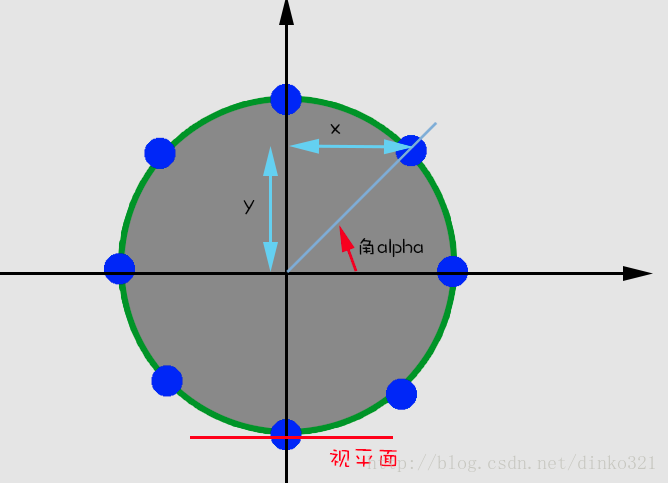
  1)、按标准坐标系，x轴正方向为0度，x轴负方向为180度。
  2)、图上的x，决定的是x方向的位置。图上的Y，是距离我们的距离，距离越远，自然就应该越小,而且距离我们越远，也就应该越靠后，zorder越低。

1.3、然后就应该补习下透视相关的东西了。请参考这里，只需要知道视椎体就行了。然后我们看侧面图：

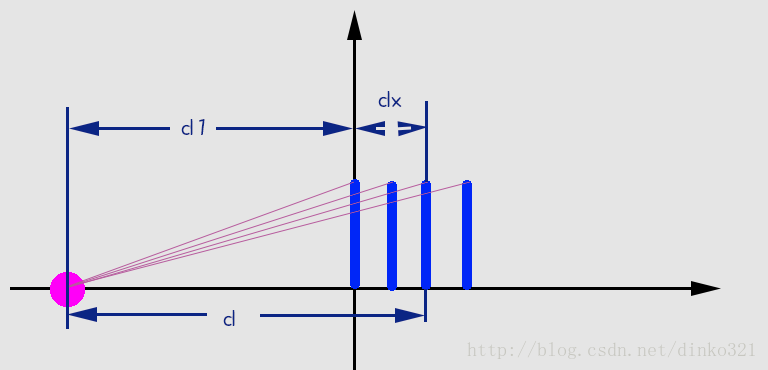
  为了方便，直接取Y轴所在平面为视平面，所做连线与Y轴的焦点，就是实际显示大小。这里涉及3个变量。物体距视点的距离d，视点到视平面之间的距离d1，视平面到物体的距离dx。设物体高度为L，物体显示高度为L'。通过相似三角形，可以轻易的得出L'的长度，但是我们其实只需要scale就够了，所以：

scale = d1 / (d1+dx)

1.3.1、但是这个d1和dx又怎么去获取，根据视椎体，有如下：

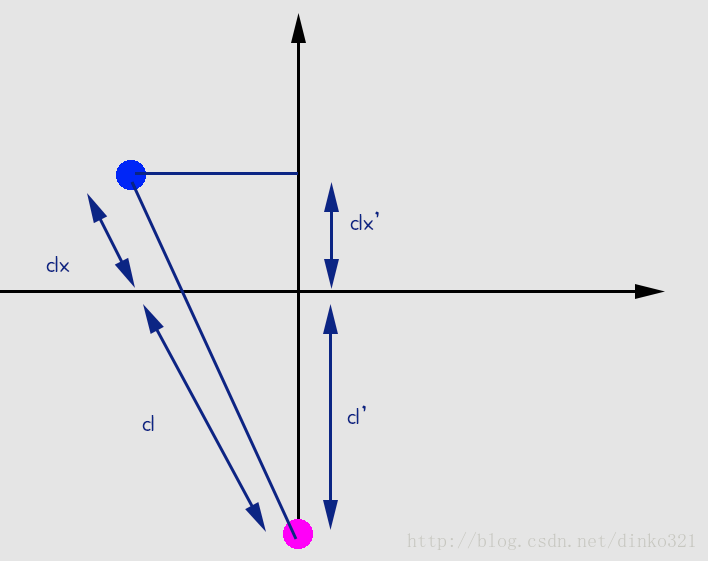
1.3.2、斜着的那个，就是上面侧面图我们要求的那个。根据相似三角形，又可以轻易得出：

scale = d' / (d' + dx ')

  这个d'和dx'，可以通过俯视图，就是上面一个圆圈圈，那个图算出来。要算这个，涉及3个变量还未知。一是角度，二是圆圈半径，3是上图的d'，也就是视点到视平面的距离。简单的说，这3个值只能自己试。。。。不过是有一定规律的角度是根据想看多少自己来分布，实际能看到的部分，只有整个园的前半圆，一共180度，加入我想一共放5个，我就按45度分布就行了。
  半径可以推测，比如我想看我全部的半圆，那么直径就是窗口的大小。
  最后一个，主要是涉及一个缩放比例，通过公式可以看出，如果d'越大，那么最前面的item和最后面的item，大小差距就越大，反之差距就越小。

1.4、角度分布

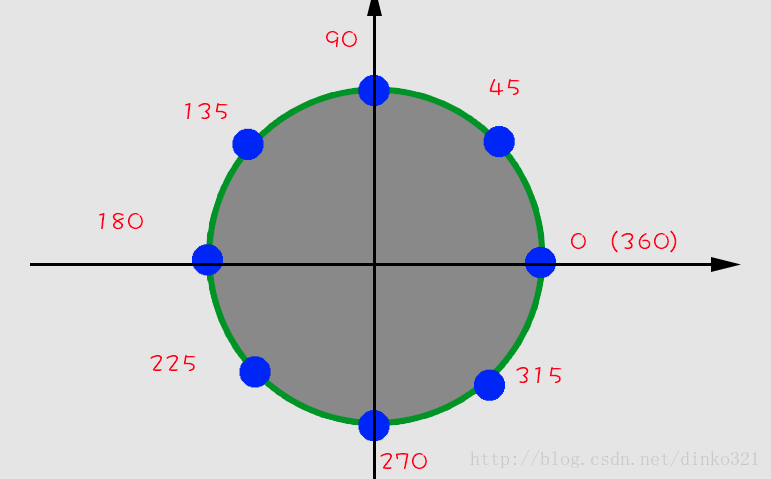
1.5、滑动增减速

  把整个过程分为2段，一段是加速，一段是减速。

  一开始滚轮静止，受到作用力，加速。然后作用力消失，受到阻力作用，减速。

  加速的时候，假设是一个匀加速运动。这一段时间的位移和时间，我们是可以获取的。通过下面，可以求得瞬时速度。

s = 0.5*a*t^2 ---- s已知，t已知 v = at ---- a上面算出

  减速这一段，假设这是一个匀减速运动。阻力恒定，那么加速度就恒定。但是这个加速度怎么取呢？我是测试了几次自己取了个值。因为我希望轻轻拨动一下，滚动的时间，大概是在1秒多这么一个范围。通过 v= at ，可以大概求出一个a，再根据实际效果，稍微调整一下。

1.6、egret代码

https://files-cdn.cnblogs.com/files/hangzi/Gallery.zip