洛谷题单指南-组合数学与计数-CF961G Partitions

原题链接：https://www.luogu.com.cn/problem/CF961G

题意解读：将1~n划分到k个非空子集，每个子集的权值是子集大小*子集内元素之和，一个划分的权值是所有子集权值之和，求所有可能的划分的权值之和。

解题思路：

观察一下样例，可以知道，答案是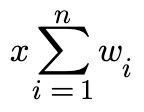

也就是，每个权值的系数相同，x怎么求？可以通过枚举不同大小的子集数来实现。

对于某个数在大小为i的子集中的情况一共有多少种？

先固定一个数，再从剩下的n-1个数选i-1个数组成一个子集，剩下的n-i个数要分成k-1个无标号非空子集，即第二类斯特林数S(n-i,k-1)，

因此，一共有种，某个数对于x的贡献还要乘以子集大小，因此一共是种；

枚举i从1到n累加得到：

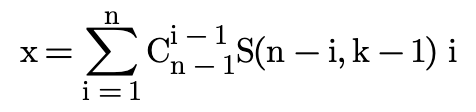
经过一番公式变换，得到：

继续推：

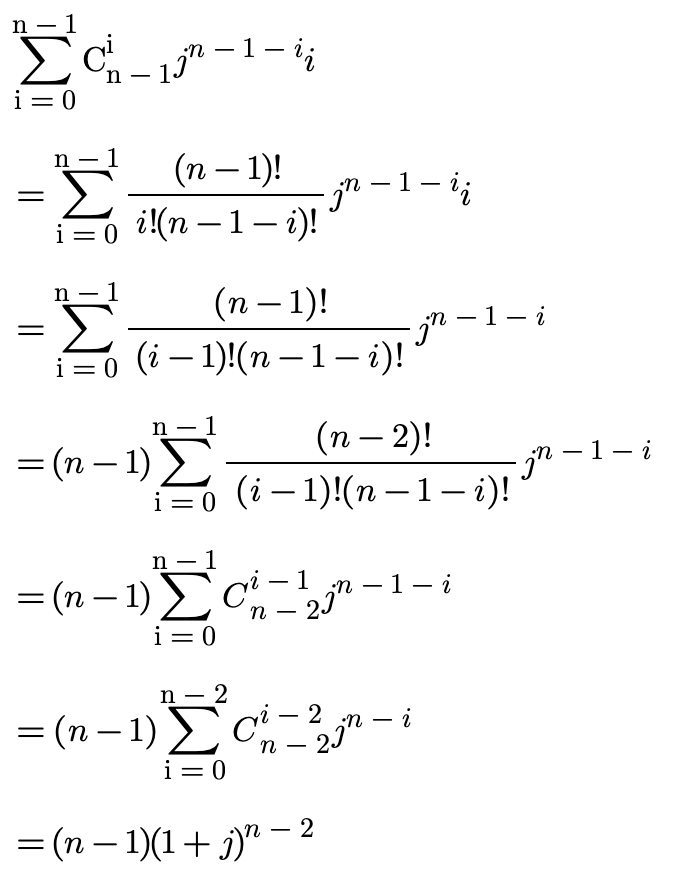
而

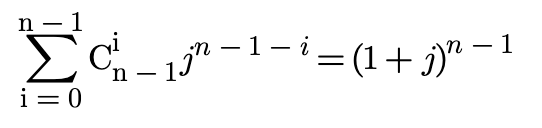
由于

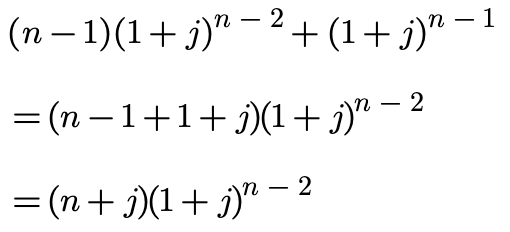
因此，最终得到x为

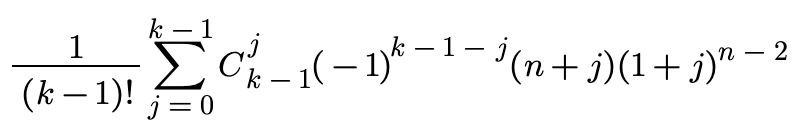
进一步简化：

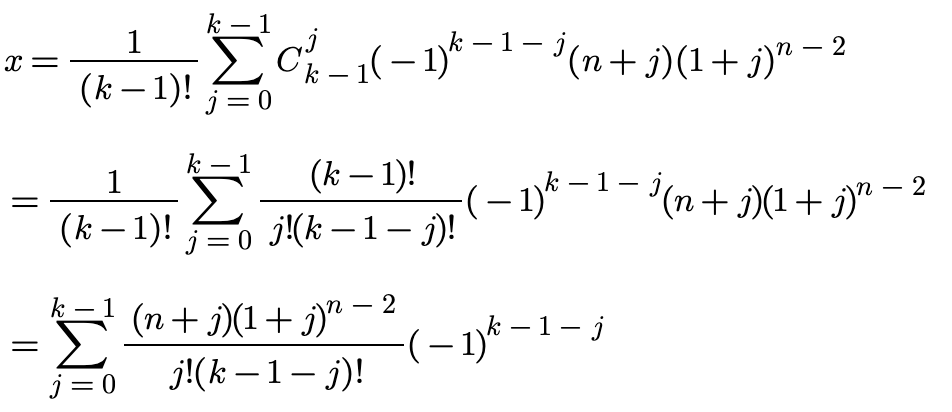
预处理阶乘的逆元，结合快速幂就可以求解了。

对于n=1要特殊处理。

100分代码：

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 200005, MOD = 1e9 + 7;
LL infac[N]; //阶乘的逆元
LL sum;
LL n, k, ans;

LL ksm(LL a, LL b, LL mod)
{
    LL res = 1;
    while(b)
    {
        if(b & 1) res = res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}

int main()
{
    cin >> n >> k;
    for(int i = 1; i <= n; i++) 
    {
        int w;
        cin >> w;
        sum = (sum + w) % MOD;
    }
    if(n == 1) 
    {
        cout << sum;
        return 0;
    } 

    //预处理阶乘的逆元
    infac[0] = 1;
    for(int i = 1; i <= k; i++)
    {
        infac[i] = infac[i - 1] * ksm(i, MOD - 2, MOD) % MOD;
    }

    for(int j = 0; j <= k - 1; j++)
    {
        LL v = (n + j) * ksm(1 + j, n - 2, MOD) % MOD;
        v = v * infac[j] % MOD * infac[k - 1 - j] % MOD;
        if(k - 1 - j & 1) ans = ((ans - v) % MOD + MOD) % MOD;
        else ans = (ans + v) % MOD;
    }

    cout << ans * sum % MOD;
    return 0;
}