洛谷题单指南-组合数学与计数-P2532 [AHOI2012] 树屋阶梯

原题链接：https://www.luogu.com.cn/problem/P2532

题意解读：平面上，一个n级阶梯由n个任意矩形拼成，求所有方案。

解题思路：

考虑一个5级阶梯：

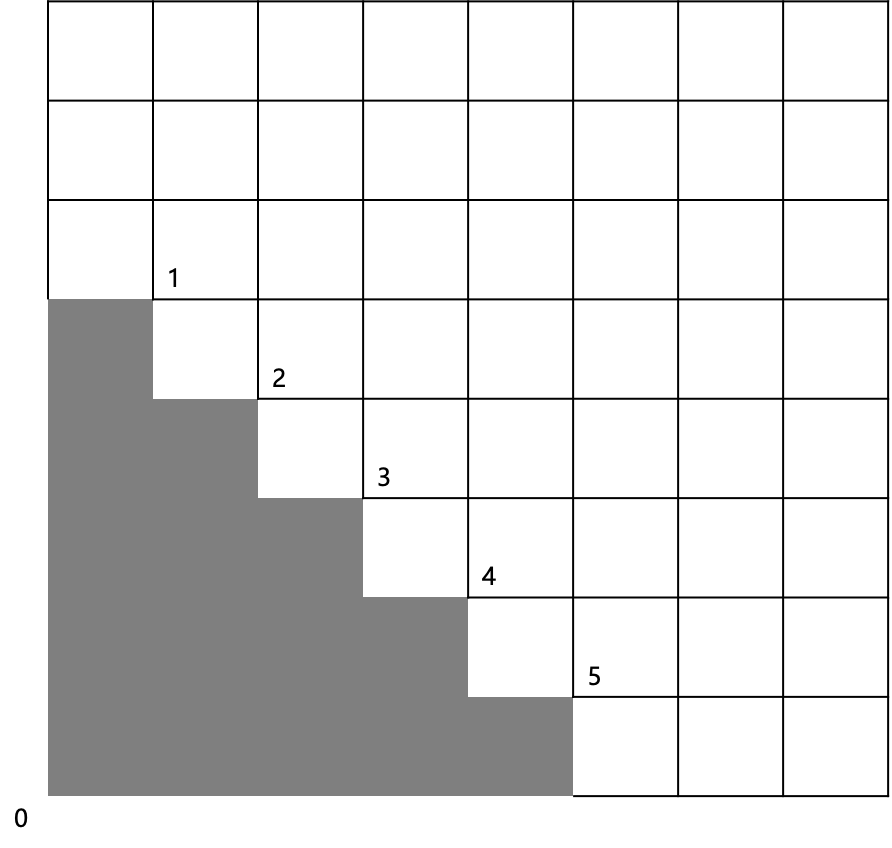
设要求的结果是f[n]，表示n级阶梯由n个矩形拼成的方案数。

一共有5个矩形，顶点1~5必然属于5个不同的矩形，因为显然任意两个不可能在同一个矩形中

再看顶点0，必然属于某一个矩形，也就是必然和1~5属于同一个矩形，那么可以枚举

1、0和1属于同一个矩形：

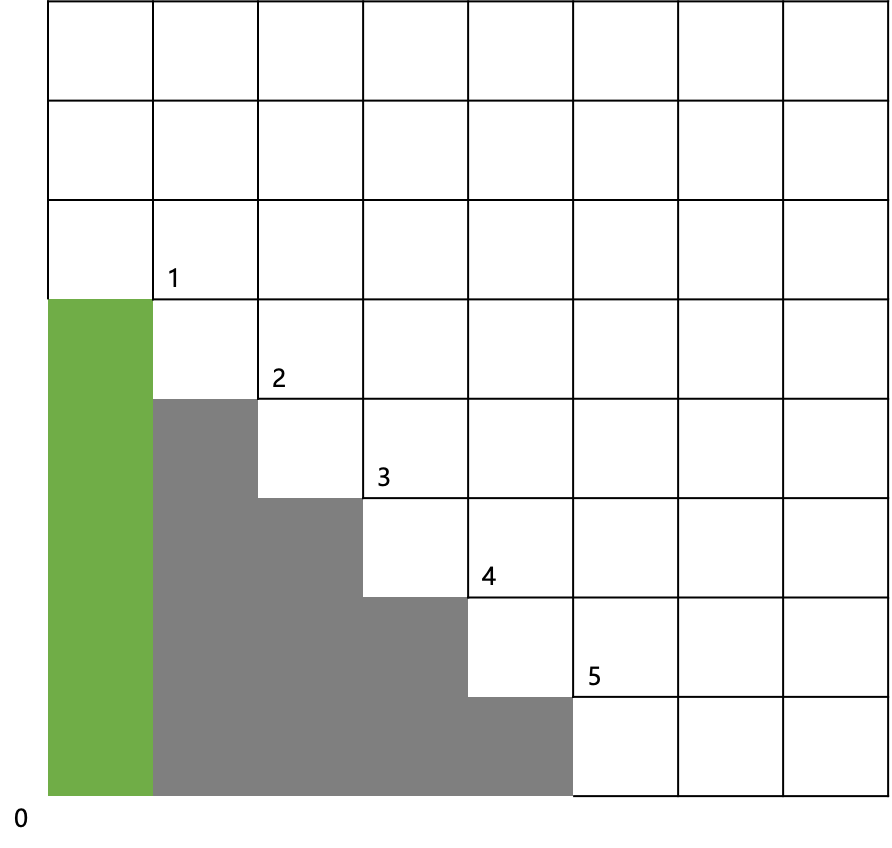
方案数为：f(0)*f(4)

2、0和2属于同一个矩形：

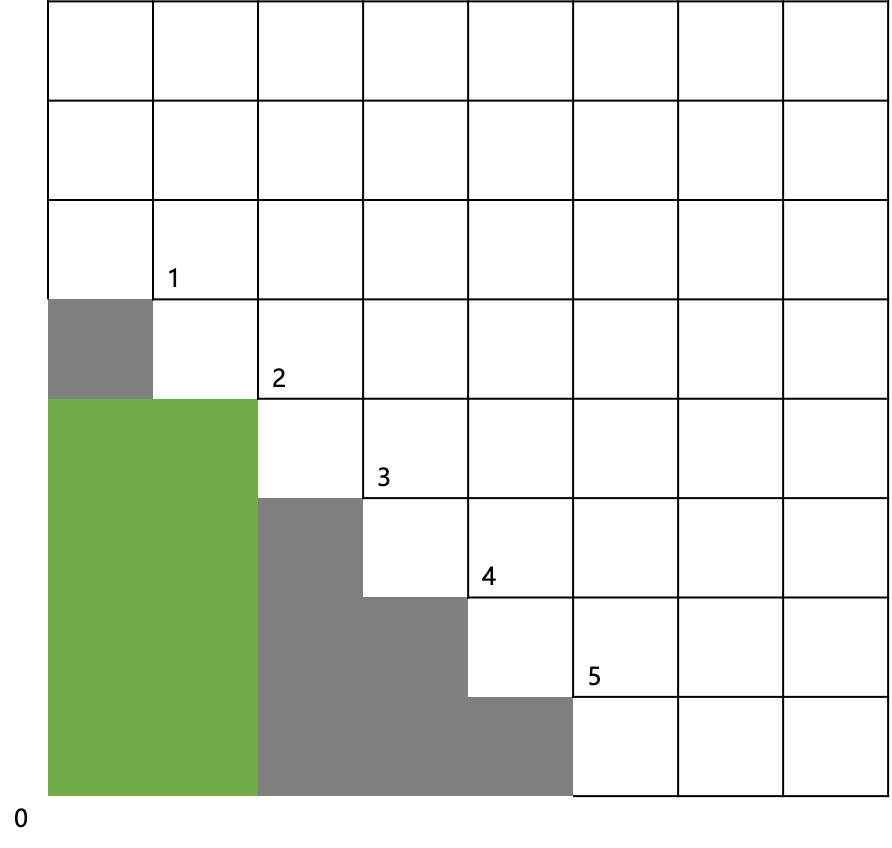
方案数为：f(1)*f(3)

3、0和3属于同一个矩形：

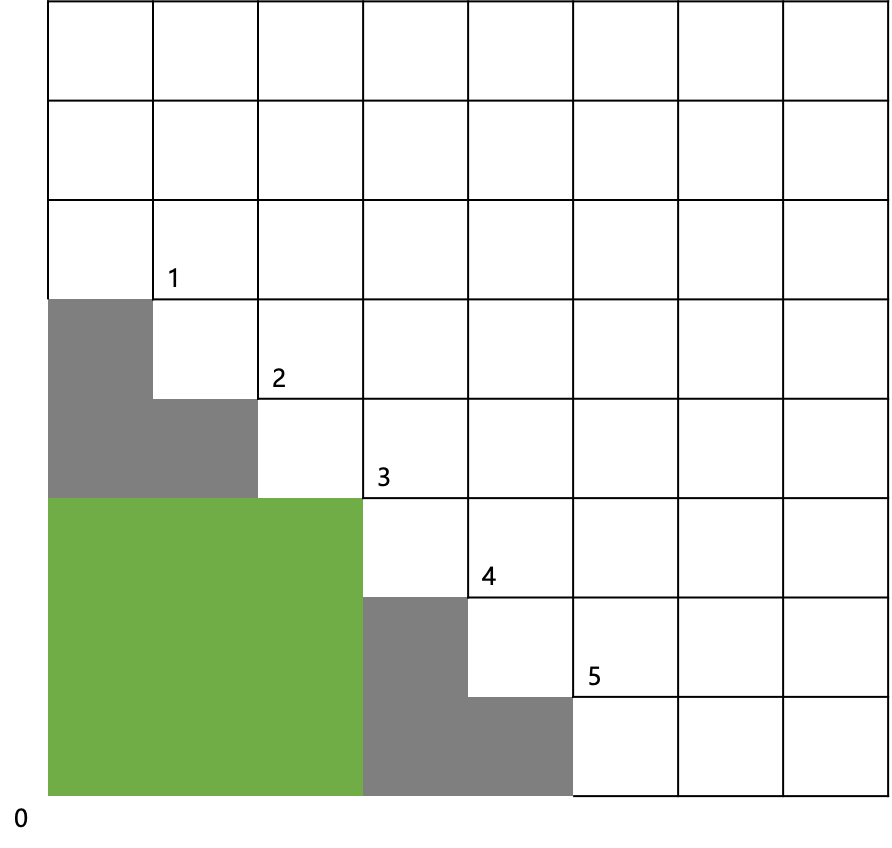
方案数为：f(2)*f(2)

4、0和4属于同一个矩形：

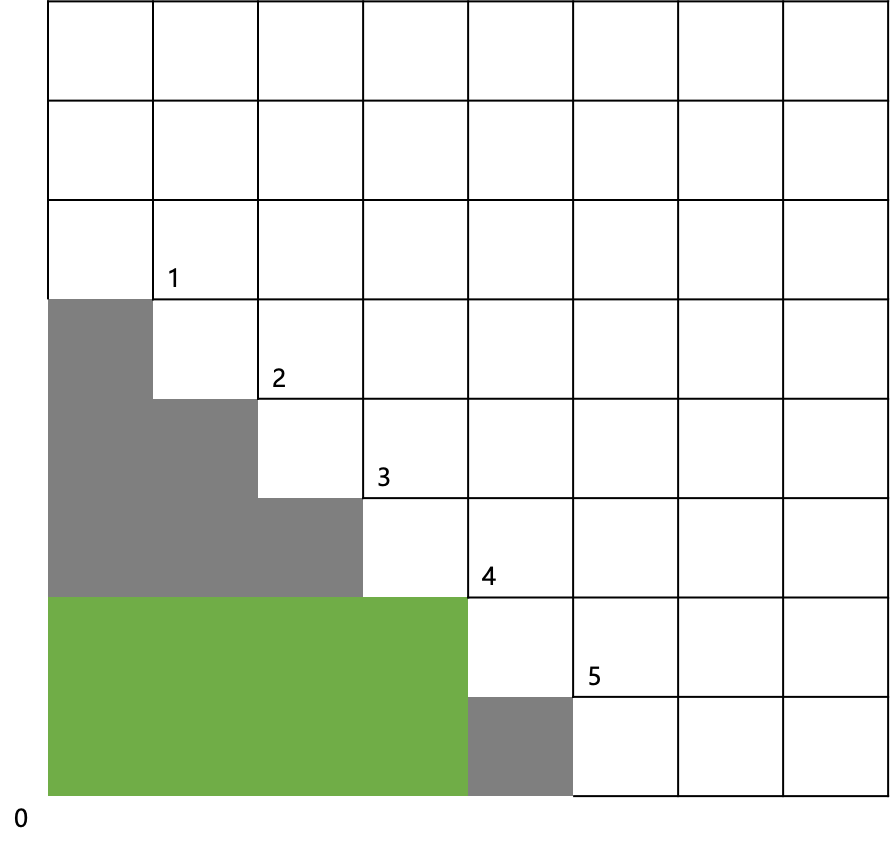
方案数为：f(3)*f(1)

5、0和5属于同一个矩形：

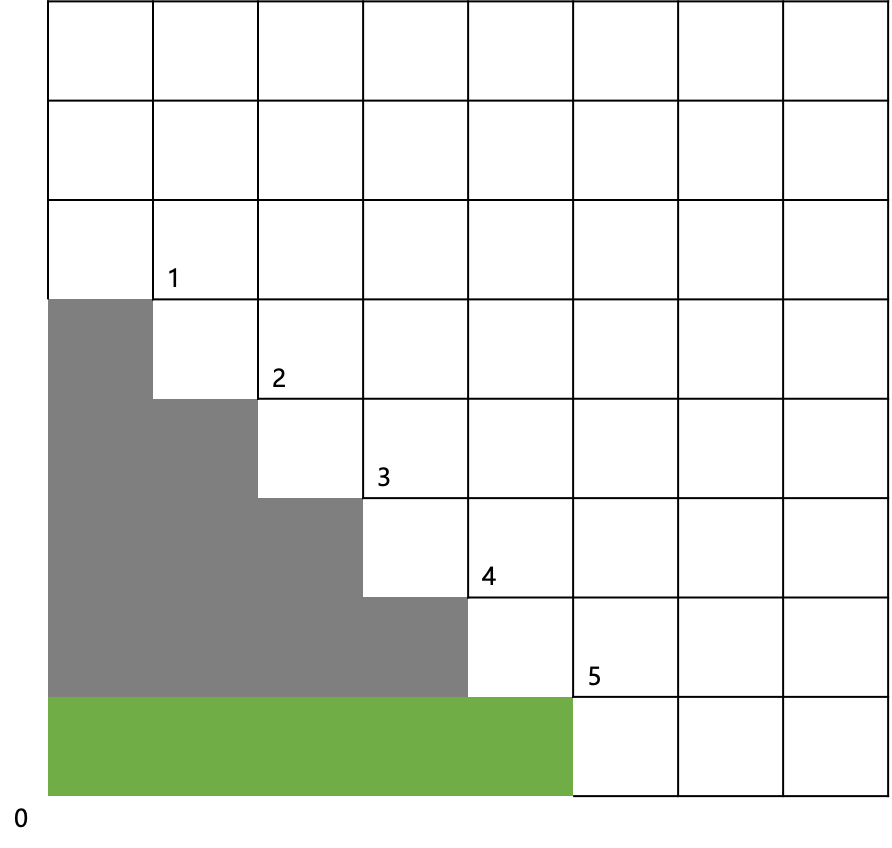
方案数为：f(4)*f(0)

因此总方案数为：f(5) = f(0)*f(4) + f(1)*f(3) + f(2)*f(2) + f(3)*f(1) + f(4)*f(0)

推而广之：f(n) = ∑f(i)*f(n-1-i)

这不就是卡特兰数！

除了递推式，卡特兰数的常见表达式如下：

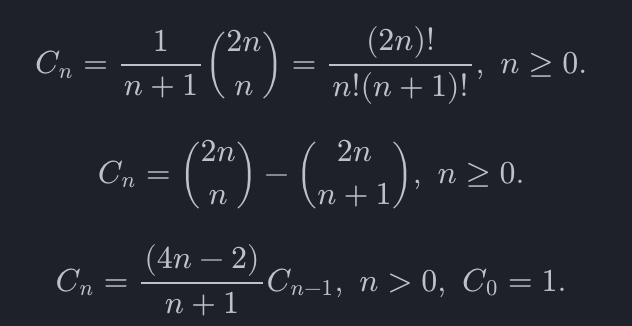
此题未做求模处理，数据很大，需要高精度，第一个式子更便于处理，可以通过对阶乘的素因子进行分解，统计所有素因子的指数。

素因子范围通过筛出2n以内所有素数即可。

小技巧：要计算n!中有多少个因子p，只需要计算n/p+n/p²+n/p³+...

最终，只需要实现高精度乘法即可。

100分代码：

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 505;
int n;
int primes[2 * N], cnt;
bool vis[2 * N];

//高精度*低精度
vector<int> mul(vector<int> &a, int b)
{
    vector<int> res;
    int t = 0;
    for(int i = 0; i < a.size(); i++)
    {
        t += a[i] * b;
        res.push_back(t % 10);
        t /= 10;
    }
    while(t)
    {
        res.push_back(t % 10);
        t /= 10;
    }
    return res;
}

//筛素数
void get_primes()
{
    for(int i = 2; i <= 2 * n; i++)
    {
        if(!vis[i]) 
        {
            primes[++cnt] = i;
            for(int j = i + i; j <= 2 * n; j += i)
                vis[j] = true;
        }
    }
}

//计算x!中素数p的幂次
int get_p(int x, int p)
{
    int res = 0;
    while(x)
    {
        res += x / p;
        x /= p;
    }
    return res;
}

int main()
{
    cin >> n;
    get_primes(); // 2n以内的素数
    vector<int> ans(1, 1); // 初始值1
    for(int i = 1; i <= cnt; i++)
    {
        int p = primes[i];
        int k = get_p(2 * n, p) - get_p(n, p) - get_p(n + 1, p); // 计算p在(2n)!/((n+1)!*n!)中的幂次
        for(int j = 1; j <= k; j++)
            ans = mul(ans, p); // ans *= p^k
    }
    for(int i = ans.size() - 1; i >= 0; i--)
        cout << ans[i];
    return 0;
}