洛谷题单指南-组合数学与计数-P5505 [JSOI2011] 分特产

原题链接：https://www.luogu.com.cn/problem/P5505

题意解读：有n种颜色的球，每种颜色有a[i]个相同的球，分成m组，每组至少有一个球的方案数。注意n和m与题目中描述相反。

解题思路：

直接计数比较困难，通过补集的角度来考虑。

1、先不考虑每组至少有一个球，所有方案

对于n中颜色的球，一个一个颜色来考虑，对于某个颜色i的a[i]个球，要任意分成m组，借助于插空法的变形，

先借m个球一共a[i]+m个球，在a[i]+m-1个空插m-1板即可，一共是C(a[i]+m-1,m-1)种。

那么对于所有颜色，根据乘法原理，一共有

2、再考虑有1组为空的方案数，应该减掉

仍然一个一个颜色来考虑，先把空的一组选出来C(m,1)，再插板，一共是C(m,1)(C(a[i]+m-2,m-2)种。

对于所有颜色，一共有

3、再考虑有2组为空的方案数，应该加上

一共有

4、以此类推，一直到m-1组为空的情况。

最终，答案是

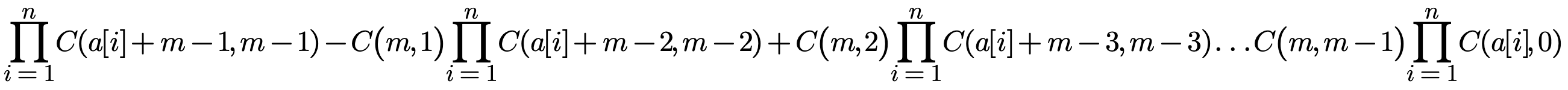
这，又是容斥原理！

进一步转化为：

组合数可以预计算，整体复杂度为O(nm)。

100分代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 2005, MOD = 1e9 + 7;
int a[N], c[N][N];
int m, n, ans;

int main()
{
    cin >> m >> n;
    for(int i = 1; i <= n; i++) cin >> a[i];

    //组合数初始化
    for(int i = 0; i <= 2000; i++)
    {
        for(int j = 0; j <= i; j++)
        {
            if(j == 0) c[i][j] = 1;
            else c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % MOD;
        }
    }

    for(int j = 0; j <= m - 1; j++)
    {
        int tmp = c[m][j];
        for(int i = 1; i <= n; i++)
        {
            tmp = 1ll * tmp * c[a[i] + m - j - 1][m - j - 1] % MOD;
        }
        if(j % 2 == 0) ans = (ans + tmp) % MOD;
        else ans = (ans - tmp + MOD) % MOD;
    }
    cout << ans;
    return 0;
}