洛谷题单指南-进阶数论-P6583 回首过去

原题链接：https://www.luogu.com.cn/problem/P6583

题意解读：1<=x,y<=n，求x/y是有限小数的个数。

解题思路：

x/y是有限小数，意味着约分之后，分母的因子只有1/2/5

因此x/y可以表示为bk/ak，a是只含2/5因子的整数，k不含2/5因子，b是任意整数，且1<=bk<=n, 1<=ak<=n

那么最简单的办法就是枚举，用tf来保存所有只含2/5因子的整数，可以提前预处理出来。

先枚举a，再枚举k，b，累加计数即可。

40分代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

LL n, ans;
vector<LL> tf; //只包含1、2、5因子的数

void init()
{
    for(int i = 1; i <= n; i *= 2)
        for(int j = 1; j * i <= n; j *= 5)
            tf.push_back(i * j);
}

int main()
{
    cin >> n;
    init();
    for(int i = 0; i < tf.size(); i++)
    {
        LL a = tf[i];
        for(int k = 1; a * k <= n; k++)
        {
            if(k % 2 == 0 || k % 5 == 0) continue;
            for(int b = 1; b * k <= n; b++)
            {
                ans++;
            }
        }
    }
    cout << ans;
    return 0;
}

观察上面代码，在对b循环时，只是从1枚举到n/k，一共n/k次，因此这层循环可以省掉，这样可以优化一层循环。

80分代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

LL n, ans;
vector<LL> tf; //只包含1、2、5因子的数

void init()
{
    for(int i = 1; i <= n; i *= 2)
        for(int j = 1; j * i <= n; j *= 5)
            tf.push_back(i * j);
}

int main()
{
    cin >> n;
    init();
    for(int i = 0; i < tf.size(); i++)
    {
        LL a = tf[i];
        for(int k = 1; a * k <= n; k++)
        {
            if(k % 2 == 0 || k % 5 == 0) continue;
            ans += n / k; //b可以选1~n/k，所以一共是n/k种选择
        }
    }
    cout << ans;
    return 0;
}

如果先枚举k，那么b的个数就是n/k，a的个数是去掉>n/k的数之后tf的个数

80分代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

LL n, ans;
vector<LL> tf; //只包含1、2、5因子的数

void init()
{
    for(int i = 1; i <= n; i *= 2)
        for(int j = 1; j * i <= n; j *= 5)
            tf.push_back(i * j);
    sort(tf.begin(), tf.end());
}

int main()
{
    cin >> n;
    init();
    for(int k = 1; k <= n; k++)
    {
        if(k % 2 == 0 || k % 5 == 0) continue; //跳过含有2或5因子的数
        while(tf.back() * k > n) tf.pop_back(); //去掉乘积大于n的数
        ans += n / k * tf.size();
    }
    cout << ans;
    return 0;
}

设f(x)表示tf中<=x的数的个数，那么上面代码其实就是

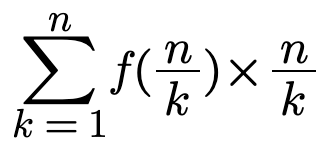
注意，与经典的整除分块算法相比，这里的区别在于k的取值不能是2或5的倍数。

当k在一个区间[l,r]中，n / k是不变的，设t = n / l

f(t)可以在循环中计算，对于每一个区间分块值就是f(t)*t*cnt，cnt表示分块中合法数的个数

分块中合法的数就是不能是2和5的倍数，可以借助于容斥原理计算：

区间[l,r]中所有数的个数为：r - l + 1

2的倍数个数为：r / 2 - (l - 1) / 2

5的倍数个数为：r / 5 - (l - 1) / 5

10的倍数个数为： r / 10 - (l - 1) / 10

因此，不难写出代码。

100分代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

LL n, ans;
vector<LL> tf; //只包含1、2、5因子的数

void init()
{
    for(LL i = 1; i <= n; i *= 2)
        for(LL j = 1; j <= n / i; j *= 5)
            tf.push_back(i * j);
    sort(tf.begin(), tf.end());
}

int main()
{
    cin >> n;
    init();
    for(LL l = 1, r; l <= n; l = r + 1)
    {
        LL t = n / l;
        if(t == 0) r = n;
        else r = n / t; 
        while(tf.size() && tf.back() > t) tf.pop_back(); //去掉不符合要求的数
        LL cnt = r - l + 1; //区间内数的个数
        cnt -= r / 2 - (l - 1) / 2; //去掉区间内含2因子的个数
        cnt -= r / 5 - (l - 1) / 5; //去掉区间内含5因子的个数
        cnt += r / 10 - (l - 1) / 10; //加上区间内含10因子的个数（被减去了两次）
        ans += t * tf.size() * cnt;
    }
    cout << ans;
    return 0;
}