洛谷题单指南-进阶数论-P2261 [CQOI2007] 余数求和

原题链接：https://www.luogu.com.cn/problem/P2261

题意解读：对于i从1到n，求k % i之和。

解题思路：

1、整除分块

整除分块（也叫数论分块）是数论中用于快速计算形如或其变形的核心技巧，核心思想是 “将函数值相同的连续区间打包计算”，把原本 O(n)复杂度的遍历优化到 O(sqrt(n))，大幅提升计算效率。

要理解整除分块，首先需明确一个关键性质：对正整数 n 和 i，函数的取值只有 O(2*sqrt(n)) 种不同结果。

  证明：

  

其次，n/i的值随着i的增大而变小，且相同的值在连续的一个区间中，所以形成分块。

那么，问题就变成要找到一个个不同值的分块[l,r]使得n/l = n/r

对于一个l，如何找r？

  当n/l != 0时，r = n / (n / l)

  证明：设n/l=k，k<=n/l<k+1，n/(k+1)<l<=n/k，l最大是n/k，因此r=n/(n/l)

  当n/l == 0时，r = n

代码实现：

int res = 0;
for(int l = 1, r; l <= n; l = r + 1)
{
    int k = n / l;
    r = n / k;
    res += k * (r - l + 1);
}

扩展：

2、问题分析

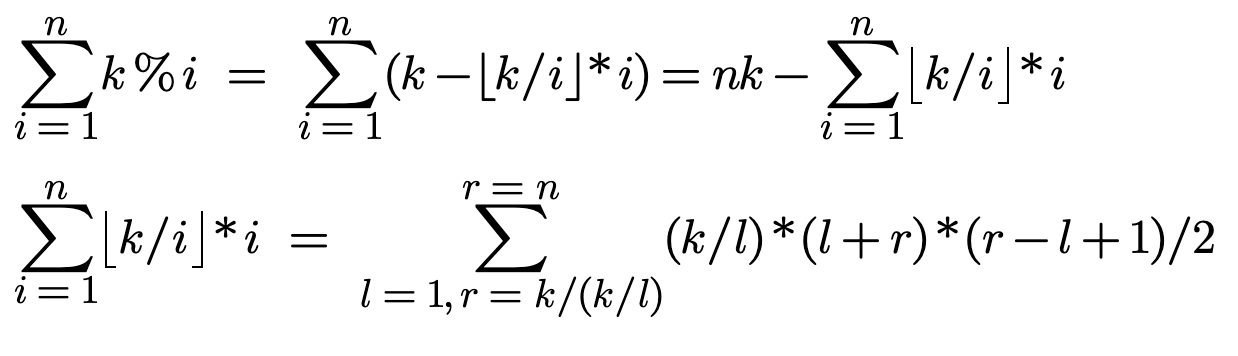
100分代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

LL n, k;

int main()
{
    cin >> n >> k;
    LL ans = n * k, sum = 0;
    for(LL l = 1, r; l <= n; l = r + 1)
    {
        if(k / l == 0) break; //避免除0
        r = k / (k / l);
        if(r > n) r = n; //限制r不超过n
        sum += (k / l) * ((l + r) * (r - l + 1) / 2);
    }
    ans -= sum;
    cout << ans;
    return 0;
}