原题链接:https://www.luogu.com.cn/problem/P4549
题意解读:求整数A1,A2,A3,...,An与任意整数X1,X2,X3...Xn组成线性方程的最小正整数解,裴蜀定理的推广应用。
解题思路:
1、裴蜀定理
对任意两个整数 a 和 b(至少有一个非零),设它们的最大公约数为 d = gcd(a, b),则:存在整数 x 和 y,使得 ax + by = d。
简单来说:“两个数的最大公约数,一定能表示成这两个数的‘整数系数线性组合’”;反之,“这两个数的所有线性组合中,最小的正整数就是它们的最大公约数”。
证明:
对任意两个整数 a > b > 0,未知数是任意值,系数大于0更易处理,欧几里得算法通过以下迭代得到 gcd(a, b)
最终非零余数 rn = gcd(a,b)
从最后一个非零余数 rn 开始,逐步将其表示为前一步两个数的线性组合,最终追溯到 a 和 b:
-
第 1 步(最后一个非零等式):rn-2 = qn rn-1 + rn,移项得:rn = rn-2 - qnrn-1这表明 rn是 rn-2和 rn-1的线性组合(系数为 1 和 -qn)。
-
第 2 步(倒推前一个等式):由 rn-3 = qn-1rn-2 + rn-1,移项得 rn-1 = rn-3 - qn-1rn-2。将 rn-1代入第 1 步的 rn表达式:rn = rn-2- qn(rn-3 - qn-1rn-2) = -qnrn-3 + (1 + qnqn-1)rn-2此时 rn表示为 rn-3和 rn-2的线性组合。
-
迭代倒推:重复上述过程,每一步都将 rn表示为 “更前一步的两个余数” 的线性组合,直到倒推至第一个等式 a = q1b + r1。
-
最终步骤:当倒推到初始的 a 和 b 时,rn(即 gcd(a,b))可表示为 a 和 b 的线性组合 ax + by(x,y为整数),定理得证。
2、裴蜀定理的推广
裴蜀定理可自然推广到任意有限个整数的情况,核心逻辑不变:
对任意 n 个整数 a1, a2, ..., an(至少一个非零),设 d = gcd(a1, a2, ... an),则:存在整数 x1, x2, ..., xn,使得 a1x1 + a2x2 + ... + anxn = d。
- 若 a1, a2, ..., an互质(即gcd(a1, a2, ..., an) = 1),则存在整数 x1, x2, ..., xn 使得 a1x1 + a2x2 + ... + anxn = 1(“互质” 的线性组合等价定义);
- 反之,若存在整数 x1, x2, ..., xn使得 a1x1 + a2x2 + ... + anxn = 1,则 a1, a2, ..., an互质(因 1 的约数只有 ±1,故最大公约数为 1)。
3、问题分析
对于此题,求所有A1~An的绝对值的GCD即可。
100分代码:
#include <bits/stdc++.h>
using namespace std;
int n, a[25];
int gcd(int a, int b)
{
return b == 0 ? a : gcd(b, a % b);
}
int main()
{
cin >> n;
if(n == 1)
{
int a;
cin >> a;
cout << abs(a);
return 0;
}
for(int i = 1; i <= n; i++) cin >> a[i], a[i] = abs(a[i]);
int d = gcd(a[1], a[2]);
for(int i = 3; i <= n; i++) d = gcd(d, a[i]);
cout << d;
return 0;
}

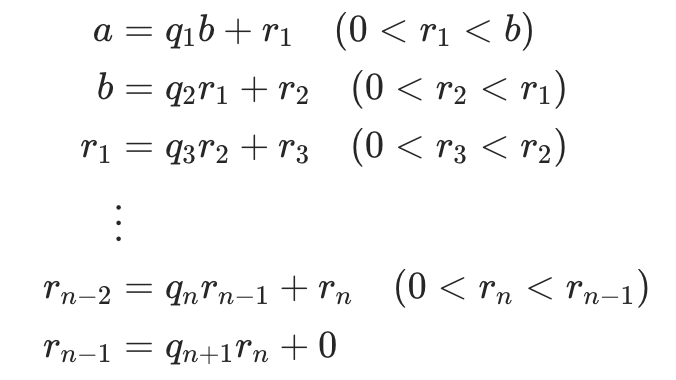

 浙公网安备 33010602011771号
浙公网安备 33010602011771号