洛谷题单指南-进阶数论-P2303 [SDOI2012] Longge 的问题

原题链接：https://www.luogu.com.cn/problem/P2303

题意解读：求1~n中所有数与n的GCD之和。

解题思路：

推公式！

根据题意，1~n中与n的GCD必然是n的因数，因此可以枚举所有n的因数，看有多少个数与n的gcd等于该因数。

据此得到初始公式：

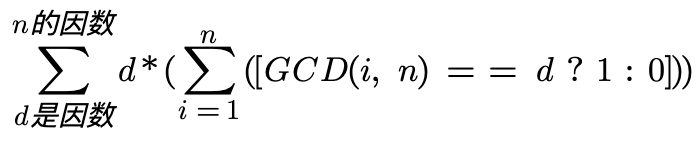
缩减d倍之后：

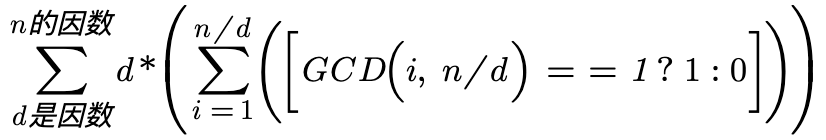
更进一步：

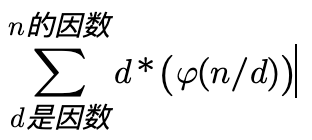
因此，先求出n的所有因数，然后对所有因数计算d*Φ(n/d)，累加即可。

100分代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

LL n, ans;

LL phi(LL x)
{
    LL res = x;
    for(LL i = 2; i <= x / i; i++)
    {
        if(x % i == 0)
        {
            res = res * (i - 1) / i;
            while(x % i == 0) x /= i;
        }
    }
    if(x != 1) res = res * (x - 1) / x;
    return res;
}

int main()
{
    cin >> n;
    for(LL i = 1; i <= n / i; i++)
    {
        if(n % i == 0)
        {
            ans += i * phi(n / i);
            if(i != n / i)
            {
                ans +=n / i * phi(i);
            }
        }
    }
    cout << ans;
    return 0;
}