洛谷题单指南-进阶数论-P2568 GCD

原题链接：https://www.luogu.com.cn/problem/P2568

题意解读：题意很简单明了，求 $1\le x,y\le n$ 且 $\gcd (x,y)$ 为素数的数对 $(x,y)$ 有多少对。

解题思路：

推公式！

根据题意要求的是所有gcd是素数的数对数量，那么可以从素数出发，看素数是多少个数对的gcd

推出原始公式：

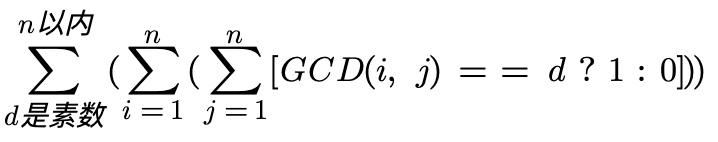
将gcd=d调整为gcd=1后公式变形为：

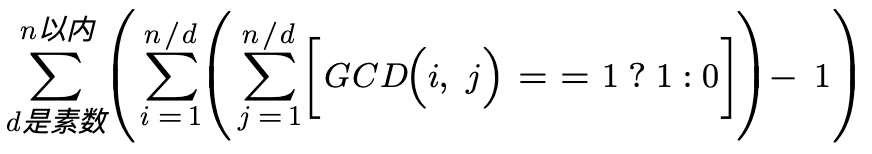
减1是因为要排除掉gcd(1,1)=1的影响，上面的式子gcd(i,j)=d不会有影响

对i从1~n/d，j从1~n/d的数对进行去重，然后用2倍计算：

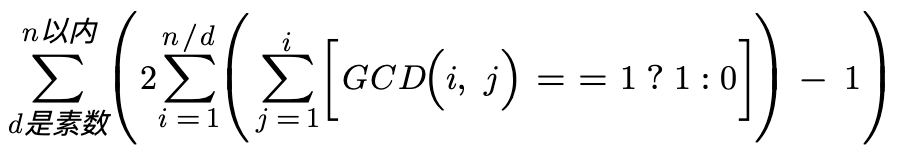
不难发现：

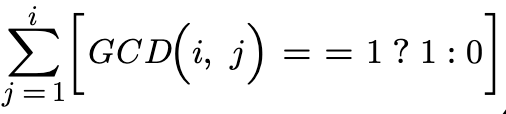就是i以内与i互质的数的个数，即欧拉函数Φ(i)

因此有：

n以内的素数，1~n/d的欧拉函数Φ(i)都可以在欧拉筛的过程中求得，最后按公式计算结果即可。

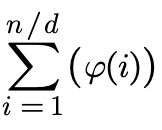可以用前缀和来优化。

100分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 10000005;
int p[N], cnt;
bool vis[N];
long long phi[N], sum[N];
int n;
long long ans;

int main()
{
    cin >> n;
    phi[1] = 1;
    for(int i = 2; i <= n; i++)
    {
        if(!vis[i])
        {
            p[++cnt] = i;
            phi[i] = i - 1;
        }
        for(int j = 1; j <= cnt; j++)
        {
            if(i * p[j] > n) break;
            vis[i * p[j]] = true;
            if(i % p[j] == 0)
            {
                phi[i * p[j]] = phi[i] * p[j];
                break;
            }
            else
            {
                phi[i * p[j]] = phi[i] * (p[j] - 1);
            }
        }
    }

    for(int i = 1; i <= n; i++) sum[i] = sum[i - 1] + phi[i];

    for(int d = 1; d <= cnt; d++)
    {
        ans += 2 * sum[n / p[d]] - 1;
    }

    cout << ans;
    return 0;
}