洛谷题单指南-状态压缩动态规划-AT_agc012_e [AGC012E] Camel and Oases

原题链接：https://www.luogu.com.cn/problem/AT_agc012_e

题意解读：坐标轴上有n个点，有一个初始跳跃值V，支持两种操作：1、V不为0时，从一点跳跃到任意一点，V=V/2； 2、从一个点可以走到相邻点，前提是两点间距离<=V，求从每个点出发是否可以遍历其他所有点，可以输出Possible，不可行输出Impossible。

解题思路：

1、建模

由于跳跃不受距离限制，能跳肯定优先跳，但是一共只能跳⌈log2(V)⌉次，其余的必须走相邻点。

每跳一次，V都会变化，以当时的V所能走的相邻点必然是连续的一段，我们可以针对所有的V，对每个点能覆盖的区域进行预处理，

用l[i][j],r[i][j]分别表示第i次跳跃之后从j点可以走到的最左、最右节点。

这样以来可以构建如下图，将每一次跳跃之后的V值以及所有节点连通性用线段表示：

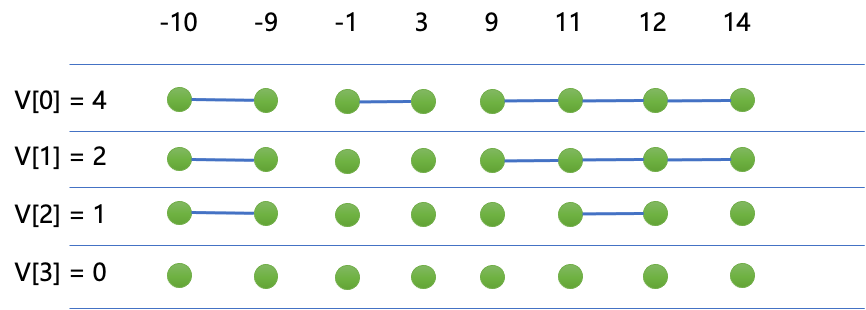
问题就变成了：是否可以在所有层各选择一条线段或者点，使得可以覆盖所有点。

2、求解

由于层数不多，可以用二进制整数对应位是否为1表示某一层是否有挑选线段，状态不包含第0层，通过以下方式定义状态：

设L[i]表示状态i下（在状态i表示的各层选择的线段）从1号点可以连续覆盖到的最右边节点

设R[i]表示状态i下（在状态i表示的各层选择的线段）从n号点可以连续覆盖到的最左边节点

其递推方式为：

i是当前状态，j是下一个要选择的层, 即对应第j次跳跃

L[i | 1 << j] = max(L[i | 1 << j], r[j][L[i] + 1])，说明：新的最右节点是前状态最右节点+1能在j层走到的最右节点；

R[i | 1 << j] = min(R[i | 1 << j], l[j][R[i] - 1] )，说明：新的最左节点是前状态最左节点-1能在j层走到的最左节点。

结果判断：

枚举第0层的每条线段[left, right]，然后枚举所有状态s的L[s]，以及其补集ss状态的R[ss]，

如果存在L[s] >= left - 1 并且 R[ss] <= right + 1，说明从状态s、ss选择的所有线段加上第0层的线段[left, right]可以覆盖所有节点，

给[left, right]内每个点的答案进行标记。

3、tips

由于一个事实，V越大，则分线段的数量越少，因此为了避免线段数量太多，可以判断如果第0层的线段数 > ⌈log2(V)⌉，则肯定不可能通过从每层选出一个线段来覆盖所有节点，直接输出结果。

4、复杂度

总体复杂度为O(v*logv)

100分代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 200005, M = 20;
int l[M][N], r[M][N];
vector<pair<int, int>> zero; //存储第0层节点连通情况，划分成若干个区间
int L[1 << M], R[1 << M];
int x[N];
bool ans[N];
int n, v;

int main()
{
    cin >> n >> v;
    for(int i = 1; i <= n; i++) cin >> x[i];
    int m;
    for(m = 0; ; m++)
    {
        l[m][1] = 1, r[m][n] = n;
        for(int j = 2; j <= n; j++) 
            l[m][j] = (x[j] - x[j - 1]) <= (v >> m) ? l[m][j - 1] : j;
        for(int j = n - 1; j >= 1; j--) 
            r[m][j] = (x[j + 1] - x[j]) <= (v >> m) ? r[m][j + 1] : j;
        if((v >> m) == 0) break; 
    }

    //统计第0层的线段
    for(int i = 1; i <= n; i++)
    {
        zero.push_back({l[0][i], r[0][i]}); //第0层的线段
    }
    sort(zero.begin(), zero.end());
    zero.erase(unique(zero.begin(), zero.end()), zero.end()); //去重

    //状态压缩dp
    for(int i = 0; i < 1 << m; i++) L[i] = 0, R[i] = n + 1; //初始化
    for(int i = 0; i < 1 << m; i++) //枚举所有状态
    {
        for(int j = 1; j <= m; j++) //枚举下一个要选择线段的层,不含0层
        {
            if(1 << (j - 1) & i) continue; //如果第j层已经选择过，跳过
            L[i | 1 << (j - 1)] = max(L[i | 1 << (j - 1)], r[j][L[i] + 1]); 
            R[i | 1 << (j - 1)] = min(R[i | 1 << (j - 1)], l[j][R[i] - 1]);
        }
    }

    if(zero.size() <= m + 1) //如果第0层线段数超过m+1，下面所有层的线段数都超过m+1，一定不可能连通
    {
        for(auto t : zero)
        {
            bool flag = false;
            for(int s = 0; s < 1 << m; s++)
            {
                int ss = (1 << m) - 1 - s; //取反
                if(L[s] >= t.first - 1 && R[ss] <= t.second + 1)
                {
                    flag = true;
                    break;
                }
            }
            if(flag)
                for(int i = t.first; i <= t.second; i++)
                    ans[i] = true; //标记区间内的点为可达
        }
    }

    for(int i = 1; i <= n; i++)
        cout << (ans[i] ? "Possible" : "Impossible") << endl;
    
    return 0;
}