洛谷题单指南-状态压缩动态规划-P4045 [JSOI2009] 密码
原题链接:https://www.luogu.com.cn/problem/P4045
题意解读:n个单词拼接成长度为l的字符串,相接处相同的前后缀可以叠在一起,问一共能拼出的字符串数量。
解题思路:
要解决这道题,首先要了解AC自动机,先来解决这道题:https://www.luogu.com.cn/problem/P5357
一、前置知识:AC自动机
1、原理
对于在字符串A中找B的问题,称之为单模式匹配问题,可以用KMP算法较好的解决:https://www.cnblogs.com/hackerchef/p/18454220
KMP算法核心原理如图:
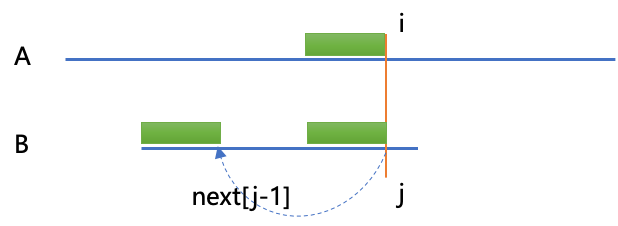
当A[i]!=B[j]时,i的位置不动,j跳转到next[j-1]的位置,继续于A[i]比较,绿色区域字符串都相等且在B中是最长前后缀,这就是KMP的核心原理。
对于在字符串A中找B、C、D。。。的问题,称之为多模式匹配问题,一个朴素想法是针对每一个模式串都跑一遍KMP,这样复杂度为O(mn)。
而AC自动机可以将多模式匹配的时间复杂度进一步优化为O(n),其原理于KMP算法类似,如图:
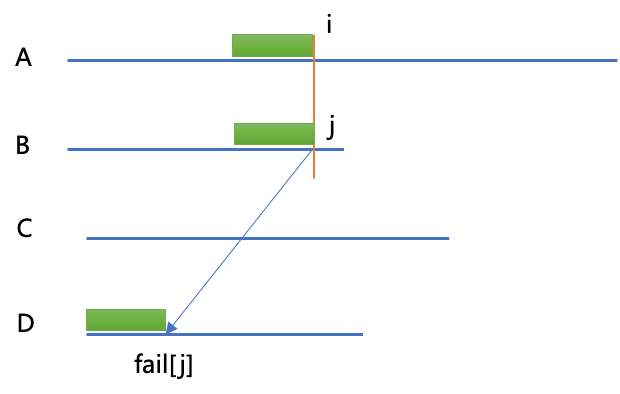
当A[i]!=B[j]是,j跳转到fail[j]的位置,用D[fail[j]]与A[i]继续比较,绿色区域字符串都相等且是最长前后缀(不同模式串的前缀和后缀),这就是AC自动机的核心原理。
2、构造
问题是如何实现在多个模式串中同时匹配并实现不同模式串的跳转,可以通过Trie树,将所有模式串加入Trie树。
以样例为例:
a
bb
aa
abaa
abaaa对以上模式串构建的trie如图所示(绿色节点表示以此节点结束有一个串)

3、匹配
先给出fail数组的定义:设fail[i]表示trie中0~fail[i]是与0~i的后缀匹配的最大前缀。比如fai[8]=4,因为8结尾的后缀aa与0~4的aa匹配且最长。
基于此定义给出其他fail值:fail[0]=0,fail[1]=0,fail[2]=0,fail[3]=2,fail[4]=1,fail[5]=2,fail[6]=1,fail[7]=4
再来如何在字符串中找模式串,对于字符串abaaabaa
首先,要在trie中找到与字符串中字符匹配的节点,如果一条路径不匹配则要通过fail跳转到匹配的位置。
其次,从trie根节点开始匹配,可以一路匹配到8号节点,此时模式串种abaa,abaaa,aa都出现过,如何记录呢?
这就需要在每匹配到一个trie中的节点x,要将该节点结尾的模式串数量记录,同时,还要记录fail[x]结尾的模式串数量,因为fail[x]结尾的串必然也匹配上了(按照fail的定义),x跳fail[x]并记录的过程不断迭代,直到x跳到0。
4、fail数组
fail数组的求法需要借助于BFS,由于每个节点的fail必然是其上层的节点,因此可以进行递推。
其规则如下:
初始,将根节点直接连接的所有节点加入队列,且fail设置为0;
依次处理队列中的节点,对于一个节点u,枚举x:a~z的路径是否存在,如果存在,则将该条路径的子节点tr[u][x]的fail值设置为u的fail值x路径的子节点:即fail[tr[u][x]] = tr[fail[u]][x],如果fail[u][x]不存在,则fail[u]继续往上跳直接找到x的路径或者跳到根节点。
76分代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 200005;
int tr[N][26], cnt[N], idx;
vector<int> words;
int fail[N], ans[N];
int q[N], l = 0, r = -1;
string txt;
int n;
void insertTrie(string s)
{
int u = 0;
for(int i = 0; i < s.size(); i++)
{
int v = s[i] - 'a';
if(!tr[u][v]) tr[u][v] = ++idx;
u = tr[u][v];
}
cnt[u] = 1; //以u结尾的单词数=1,不能cnt[u]++,因为要去重
words.push_back(u);
}
void buildFail()
{
for(int i = 0; i < 26; i++)
{
if(tr[0][i]) q[++r] = tr[0][i];
}
while(l <= r)
{
int u = q[l++];
for(int i = 0; i < 26; i++)
{
int v = tr[u][i]; //遍历u的子节点
if(v) //如果子节点存在
{
int t = fail[u];
while(t && !tr[t][i]) t = fail[t]; //t不断找到使得tr[t][i]存在的位置
if(tr[t][i]) t = tr[t][i]; //t往下走
fail[v] = t; //fail[v]指向t,使得v结尾的后缀与tr[t][i]结尾的前缀相同且最长
q[++r] = v;
}
}
}
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i++)
{
string s;
cin >> s;
insertTrie(s);
}
cin >> txt;
buildFail();
for(int i = 0, j = 0; i < txt.size(); i++)
{
int x = txt[i] - 'a';
while(j && !tr[j][x]) j = fail[j]; //j跳到能跟txt[i]去匹配的位置
if(tr[j][x]) j = tr[j][x];
int t = j;
while(t) //将所有匹配的字串统计入答案,一旦tr[j][x]匹配,fail[tr[j][x]]...一路往上跳都匹配
{
ans[t] += cnt[t];
t = fail[t];
}
}
for(auto i : words)
cout << ans[i] << endl;
return 0;
}5、优化一
超时的关键点有两个:
第一、建立fail和匹配时,要不断往上跳使得tr[t][i]存在
第二、匹配时,要不断往上跳以将所有的子串匹配都找出来
对于第一个问题,通过建立trie图来优化,也就是对于不存在的trie节点,也指向父节点对应字符的位置;而对于存在的点则建立起fail指向父节点fail对应的字符位置:
if(!v) tr[u][i] = tr[fail[u]][i];
else
{
fail[v] = tr[fail[u]][i];
q[++r] = v;
}对于第二个问题,在匹配每一个trie节点是,都记录一次次数,通过对fail指针逆向建图,然后跑dfs计算子树和即可实现单词出现次数的统计。
100分代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 200005;
int tr[N][26], cnt[N], idx;
vector<int> words;
int fail[N], ans[N];
int head[N], to[N], nxt[N], idx2;
int q[N], l = 0, r = -1;
string txt;
int n;
void insertTrie(string s)
{
int u = 0;
for(int i = 0; i < s.size(); i++)
{
int v = s[i] - 'a';
if(!tr[u][v]) tr[u][v] = ++idx;
u = tr[u][v];
}
cnt[u] = 1; //以u结尾的单词数=1,不能cnt[u]++,因为要去重
words.push_back(u);
}
void buildFail()
{
for(int i = 0; i < 26; i++)
{
if(tr[0][i]) q[++r] = tr[0][i];
}
while(l <= r)
{
int u = q[l++];
for(int i = 0; i < 26; i++)
{
int v = tr[u][i]; //遍历u的子节点
if(!v) tr[u][i] = tr[fail[u]][i];
else
{
fail[v] = tr[fail[u]][i];
q[++r] = v;
}
}
}
}
void add(int a, int b)
{
to[++idx2] = b;
nxt[idx2] = head[a];
head[a] = idx2;
}
void dfs(int u)
{
for(int i = head[u]; ~i; i = nxt[i])
{
int v = to[i];
dfs(v);
ans[u] += ans[v];
}
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i++)
{
string s;
cin >> s;
insertTrie(s);
}
cin >> txt;
buildFail();
for(int i = 0, j = 0; i < txt.size(); i++)
{
int x = txt[i] - 'a';
j = tr[j][x];
ans[j]++; //记录节点j出现的次数
}
//根据fail建反向图
memset(head, -1, sizeof(head));
for(int i = 1; i <= idx; i++)
add(fail[i], i);
dfs(0); //求每个节点的子树和
for(auto i : words)
cout << ans[i] << endl;
return 0;
}6、优化二
通过拓扑序递推同样可以实现dfs求子树和的效果,而队列中入队的顺序,正好就是fail指标反图的拓扑序,逆着拓扑序将节点的次数累加到其父节点即可。
100分代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 200005;
int tr[N][26], idx;
vector<int> words;
int fail[N], ans[N];
int head[N], to[N], nxt[N], idx2;
int q[N], l = 0, r = -1;
string txt;
int n;
void insertTrie(string s)
{
int u = 0;
for(int i = 0; i < s.size(); i++)
{
int v = s[i] - 'a';
if(!tr[u][v]) tr[u][v] = ++idx;
u = tr[u][v];
}
words.push_back(u);
}
void buildFail()
{
for(int i = 0; i < 26; i++)
{
if(tr[0][i]) q[++r] = tr[0][i];
}
while(l <= r)
{
int u = q[l++];
for(int i = 0; i < 26; i++)
{
int v = tr[u][i]; //遍历u的子节点
if(!v) tr[u][i] = tr[fail[u]][i];
else
{
fail[v] = tr[fail[u]][i];
q[++r] = v;
}
}
}
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i++)
{
string s;
cin >> s;
insertTrie(s);
}
cin >> txt;
buildFail();
for(int i = 0, j = 0; i < txt.size(); i++)
{
int x = txt[i] - 'a';
j = tr[j][x];
ans[j]++; //记录节点j出现的次数
}
//入队的顺序即反向见图后的拓扑序,逆拓扑序遍历,将子节点累加到父节点
for(int i = r; i >= 0; i--)
ans[fail[q[i]]] += ans[q[i]];
for(auto i : words)
cout << ans[i] << endl;
return 0;
}二、开胃小菜
搞懂了AC自动机,接下来,看看另外两道题,为这道题做做铺垫
相关题目1:https://www.acwing.com/problem/content/1054/
对于包不包含子串,可以通过KMP匹配的过程来判断,在KMP匹配的过程中,根据下一次要匹配的原字符串位置以及模式串的位置的跳转,可以实现状态的转移。
设f[i][j]表示在KMP过程中当前S串匹配了i位,模式串T匹配到j时所产生的S串的数量;
100分代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 55, MOD = 1e9 + 7;
int f[N][N];
int ne[N];
string t;
int n;
int main()
{
cin >> n >> t;
//构建next数组
for(int i = 1, j = 0; i < t.size(); i++)
{
while(j && t[i] != t[j]) j = ne[j - 1];
if(t[i] == t[j]) j++;
ne[i] = j;
}
//动态规划
f[0][0] = 1;
for(int i = 0; i < n; i++) //枚举S已经匹配的长度
{
for(int j = 0; j < t.size(); j++) //枚举T匹配到的位置
{
for(char k = 'a'; k <= 'z'; k++) //枚举下一个匹配的字母
{
int x = j; //下一个匹配的T的位置
while(x && t[x] != k) x = ne[x - 1];
if(t[x] == k) x++;
//状态转移,x不能走到t的最后一个位置,因为S不包含T
if(x == t.size()) continue;
f[i + 1][x] = (f[i + 1][x] + f[i][j]) % MOD; //状态转移,累加方案数
}
}
}
int ans = 0;
for(int i = 0; i < t.size(); i++) ans = (ans + f[n][i]) % MOD; //将最后匹配到模式串每个为止的方案数累加
cout << ans;
return 0;
}相关题目2:https://www.acwing.com/problem/content/1055/
此题要在字符串中修改最少的字符,使得不包含多个模式串,由此可以想到AC自动机
在AC自动机建立时,一个trie节点所表示的字符是否是非法模式串的结尾,可以通过flag[i] |= flag[fail[i]]计算
设f[i][j]表示待修复字符串匹配了前i个,trie中模式串匹配到j号节点时的最少修改次数
在匹配过程中,通过下一个匹配节点是否与预期字符相等,决定是否要修改,不相等则说明修改了一次,而通过下一个要匹配的节点可以实现状态转移。
100分代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1005, INF = 0x3f3f3f3f;
int tr[N][4], fail[N], idx; //ac自动机
bool flag[N]; //flag[i]表示以i节点结尾有致命片段,或者i往fail[i]不断往上跳存在致命片段
int f[N][N]; //f[i][j]表示待修复字符串匹配了前i个,trie中模式串匹配到j号节点时的最少修改次数
string s;
int t, n;
int trans(char c)
{
if(c == 'A') return 0;
if(c == 'G') return 1;
if(c == 'C') return 2;
if(c == 'T') return 3;
}
void insertTrie(string s)
{
int u = 0;
for(int i = 0; i < s.size(); i++)
{
int x = trans(s[i]);
if(!tr[u][x]) tr[u][x] = ++idx;
u = tr[u][x];
}
flag[u] = 1;
}
void buildFail()
{
queue<int> q;
for(int i = 0; i < 4; i++)
{
if(tr[0][i]) q.push(tr[0][i]);
}
while(q.size())
{
int u = q.front(); q.pop();
for(int i = 0; i < 4; i++)
{
int v = tr[u][i];
if(!v) tr[u][i] = tr[fail[u]][i];
else
{
fail[v] = tr[fail[u]][i];
flag[v] |= flag[fail[v]]; //考虑子串,避免往上跳
q.push(v);
}
}
}
}
int main()
{
while(cin >> n && n != 0)
{
t++;
memset(tr, 0, sizeof(tr));
memset(flag, 0, sizeof(flag));
memset(fail, 0, sizeof(fail));
memset(f, 0x3f, sizeof(f));
idx = 0;
for(int i = 1; i <= n; i++)
{
cin >> s;
insertTrie(s);
}
cin >> s;
//s = " " + s;
buildFail();
f[0][0] = 0;
for(int i = 0; i < s.size(); i++) //枚举所有已匹配的字符串长度
{
for(int j = 0; j <= idx; j++) //枚举所有当前可能匹配到的trie树节点
{
for(int k = 0; k < 4; k++) //枚举下一个可能匹配的字符
{
int t = tr[j][k]; //下一个节点
int cost = trans(s[i]) != k; //下一个匹配的字符如果等于k,说明不需要修改;不等于k则表示修改了一处
//没有匹配到非法串
if(!flag[t]) f[i + 1][t] = min(f[i + 1][t], f[i][j] + cost);
}
}
}
int ans = INF;
for(int i = 0; i <= idx; i++) ans = min(ans, f[s.size()][i]);
if(ans == INF) ans = -1;
cout << "Case " << t << ": " << ans << endl;
}
return 0;
}三、进入正餐
回到此题,要统计所有单词拼出特定长度的字符串数量,由于首尾部分可以重叠,显然可以用AC自动机。
设f[i][j][k]表示当前匹配了i个字符,trie节点匹配到j,匹配上的单词状态为k的方案数,
枚举字符串长度,枚举trie节点,枚举单词状态,再枚举下一个匹配的字符,根据AC自动机匹配的trie节点跳转可以实现状态转移:
f[i + 1][tr[j][l]][k | cnt[tr[j][l]]] += f[i][j][k];
在建立trie以及构建AC自动机的过程中,用cnt[i]来包括i节点结尾的所有单词的状态。
如此即可统计所有的字符串数量。
对于数据具体方案,需要拆分为两步:
第一步:通过dfs来计算g[a][b][c]是否能走到g[n][...][(1<<m)-1],n是字符串长度,m是单词数量,也就是能够走到终态,能走到终态意味着转移所走的字符是结果中的字符,注意需要用记忆化剪枝来优化。
100分代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 30, M = 105, K = 1 << 10;
int tr[M][26], cnt[M], idx; //cnt[i]表示以i节点的字符结尾的所有模式串的状态,通过cnt[i] |= cnt[fail[i]]计算
int fail[M];
LL f[N][M][K]; //f[i][j][k]表示当前匹配了i个字符,trie节点匹配到j,匹配上的单词状态为k的方案数
bool g[N][M][K], vis[N][M][K]; //g[a][b][c]标识从当前状态是否能到达终态:达到预期长度,所有单词都用上,vis用作记忆化剪枝
int n, m;
void insertTrie(string s, int id)
{
int u = 0;
for(int i = 0; i < s.size(); i++)
{
int x = s[i] - 'a';
if(!tr[u][x]) tr[u][x] = ++idx;
u = tr[u][x];
}
cnt[u] |= (1 << id); //以u结尾的模式串合并状态
}
void buildFail()
{
queue<int> q;
for(int i = 0; i < 26; i++)
{
if(tr[0][i]) q.push(tr[0][i]);
}
while(q.size())
{
int u = q.front(); q.pop();
for(int i = 0; i < 26; i++)
{
int v = tr[u][i];
if(!v) tr[u][i] = tr[fail[u]][i];
else
{
fail[v] = tr[fail[u]][i];
cnt[v] |= cnt[fail[v]]; //以v的字符结尾的模式串合并状态
q.push(v);
}
}
}
}
void dp()
{
f[0][0][0] = 1;
for(int i = 0; i < n; i++)
{
for(int j = 0; j <= idx; j++)
{
for(int k = 0; k < (1 << m); k++)
{
for(int l = 0; l < 26; l++)
{
f[i + 1][tr[j][l]][k | cnt[tr[j][l]]] += f[i][j][k]; //trie节点跳转到tr[j][l],状态k合并上tr[j][l]的状态
}
}
}
}
}
//dfs1(a,b,c)表示从当前状态能否到达终态
bool dfs1(int a, int b, int c)
{
if(vis[a][b][c]) return g[a][b][c];
vis[a][b][c] = true;
if(a == n && c == (1 << m) - 1) g[a][b][c] = true; //终态
if(a < n)
{
for(int i = 0; i < 26; i++)
{
g[a][b][c] |= dfs1(a + 1, tr[b][i], c | cnt[tr[b][i]]); //当前状态能否到终态取决于下一个状态能否到终态
}
}
return g[a][b][c];
}
void dfs2(int a, int b, int c, string word)
{
if(a == n && c == (1 << m) - 1)
{
cout << word << endl;
return; //输出一个满足条件的单词
}
for(int i = 0; i < 26; i++)
{
if(!g[a + 1][tr[b][i]][c | cnt[tr[b][i]]]) continue; //如果下一个状态不能到终态,跳过
char cur = 'a' + i;
dfs2(a + 1, tr[b][i], c | cnt[tr[b][i]], word + cur); //继续dfs下一个字符
}
}
int main()
{
cin >> n >> m;
for(int i = 0; i < m; i++)
{
string s;
cin >> s;
insertTrie(s, i);
}
buildFail();
dp();
LL ans = 0;
for(int i = 0; i <= idx; i++) ans += f[n][i][(1 << m) - 1]; //统计所有状态下,匹配到n个字符且所有单词都用上的方案数
cout << ans << endl;
if(ans <= 42)
{
dfs1(0, 0, 0); //dfs1用于判断从当前状态是否能到达终态
dfs2(0, 0, 0, ""); //dfs2用于输出满足条件的单词
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号